DME/DME区域导航的导航台优选算法

沈笑云，褚世超，焦卫东，孟 健

（中国民航大学天津市智能信号和图像处理重点实验室，天津 300300）

区域导航（regional navigation，RNAV）作为一种导航方式，与传统空中交通服务航路不同，它可以使航空器在导航信号覆盖范围内，或在机载自备导航设备的工作范围内，或二者的结合情况下，沿任意期望的航迹飞行[1]。其具有航路设置非常灵活，增加空域容量，且不依赖于地面导航设备位置的特点[2]。目前在交通密度较大的空域，区域导航航路的主要导航方式为DME/DME[3]。由于DME/DME不要求对机载导航设备做任何改变，且比其他导航方式需要更少的导航台数，因此DME/DME导航方式在区域导航中越来越受到重视[4]。传统的DME/DME导航台选择算法是根据飞机当前的位置，选择与飞机几何位置关系最好的一对DME进行导航，但在文献[5-6]中都指出，在地面导航台分布密集的地区，传统的DME导航台选择算法会出现导航台频繁切换的问题，严重影响了定位的精确性和连续性。尤其随着DME导航台布设数量的增加，传统DME导航台选择算法的缺点将越来越明显，并会带来很大的安全隐患。

针对这一问题，本文根据DME/DME区域导航在航路阶段的要求，对传统的DME导航台自动选择算法进行了改进：分析了满足DME/DME区域导航的要求，提出了避免频繁切换的DME/DME导航台选择算法，利用Matlab建立了导航台自动选择模型，以A593航路为例进行了仿真实验来验证该算法的有效性，并将结果与传统选台算法进行了对比和分析，最后对选台结果的DME/DME区域导航性能进行了评估。仿真结果表明：该算法可在一定程度降低DME切换频率，并能满足区域导航的精度要求，提高了选台算法的稳定性。

1 DME/DME区域导航的原理及传统算法

1.1 DME导航原理

DME（distance measurement equipment）导航系统由机载测距机和地面测距信标台组成，DME系统通过询问应答方式来测量飞机到地面导航台的斜距。用于区域导航时需要同时接收2个或2个以上DME信号，才能确定飞机的位置。DME/DME区域导航定位的原理如图1所示。

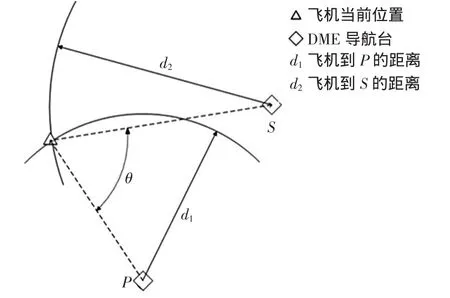
图1 DME/DME定位原理Fig.1 Positioning principle of DME/DME

目前，中国区域导航的主要导航方式是VOR/DME和DME/DME[7-8]。考虑到DME/DME的导航精度高于VOR/DME[9]，本文针对DME/DME区域导航航路进行研究。导航台自动选择算法要保证有效性、可靠性和实时性，同时要满足区域导航性能的要求。

1.2 DME/DME区域导航的要求

1）理论有效的DME

根据PBN Manual规定，DME台到飞机的距离大于160 n mile和小于3 n mile的DME均不可参与基于性能的导航（performance based navigation，PBN）。因此，如果航路点到各DME的水平距离L满足

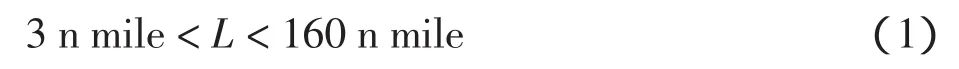
则该DME可用于DME/DME区域导航，这些DME为理论有效的DME。

2）有效 DME 对

在航路阶段，若无法接收到2个符合条件的DME导航台信号时，则选择VOR/DME导航方式[10]。使用DME/DME进行区域导航时，飞机通过2台或更多的DME的交角计算其位置，如果仅能接受2台DME的输入，那么飞机和DME对构成的夹角必须在30°～150°之间，此时的DME对为有效DME对，而最优DME对的夹角为90°左右，其精度可达到0.1 n mile。

3）DME/DME的有效导航区域

DME/DME区域导航要求飞机必须在所选有效DME对的有效导航区域内任意飞行。首先假设P和S分别为2个DME导航台，以2个导航台为圆心，分别以3 n mile和160 n mile为半径画圆，如图2中4个实线圆。然后以2个导航台之间距离为半径，同时过2个导航台画2个虚线圆，如图2中所示。在虚线圆中，P和S两点所连接的小弧和大弧对应的圆心角分别为60°和 300°，其所对应的圆周角分别为 30°～150°，要满足30°≤W≤150°这一条件，需用2个大实线圆的相交区域减去2个虚线圆的相交区域（即大于150°的盲区区域）即得到2个DME导航台的有效导航区域，如图2中阴影部分。在实际中由于受地形、建筑等影响，DME的覆盖范围不是严格的圆形，且与飞机所在高度有关[11]，此处由于考虑到区域导航航路飞机高度大于12 000 ft（1 ft=0.304 8 m），因此未考虑地形对DME信号遮蔽影响，默认DME的覆盖范围为圆形。

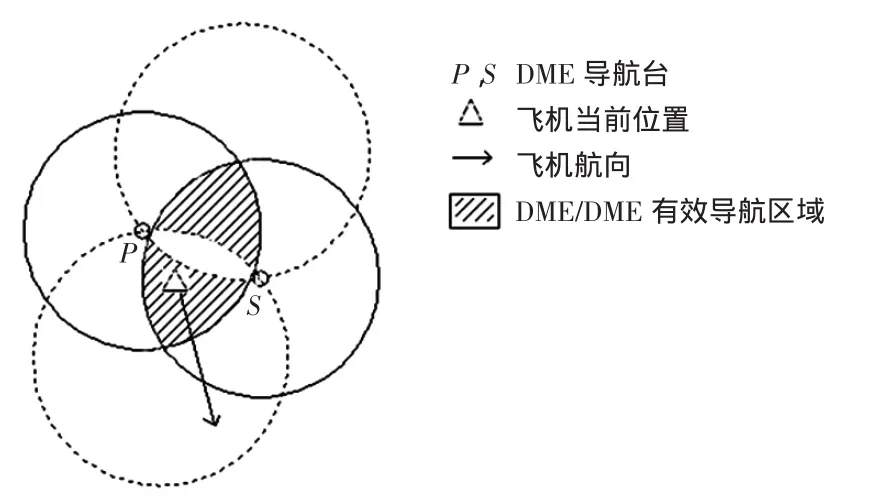
图2 DME/DME的有效导航区域Fig.2 Effective navigation area of DME/DME

1.3 传统导航台选择算法

传统DME导航台选择算法：使DME对与飞机位置连线夹角尽可能接近90°的为最佳DME对，虽然能够选出一对角度最好的导航台，在任何时刻、任何航路点提供尽可能准确的飞机位置信息，但是当整个航路应用此方法的时候，这样的选台标准存在明显的缺点——当飞机飞过地面导航台分布密集的区域时，会出现导航台频繁跳变的问题。目前导航台切换要求有大概5 s的初始化延迟时间，因此，导航台的频繁切换会降低飞机位置估计的可靠性和连续性[6]。尤其随着未来布设DME导航台的数量增加，传统算法中导航台频繁切换将影响定位的连续性，从而影响定位的精度。在传统方法中，通过对定位精度设定某个阈值，当航路点的定位精度不小于该阈值时，就不切换DME导航台。此方法的缺点是：为了使导航台切换频率降低，需设定一个相对较低的阈值，因此在航路中不能维持较高的定位精度。

2 本文算法

针对传统算法中导航台频繁跳变这一问题，本文对传统的DME导航台选择算法进行了改进，图3为本文导航台自动选择算法流程图。

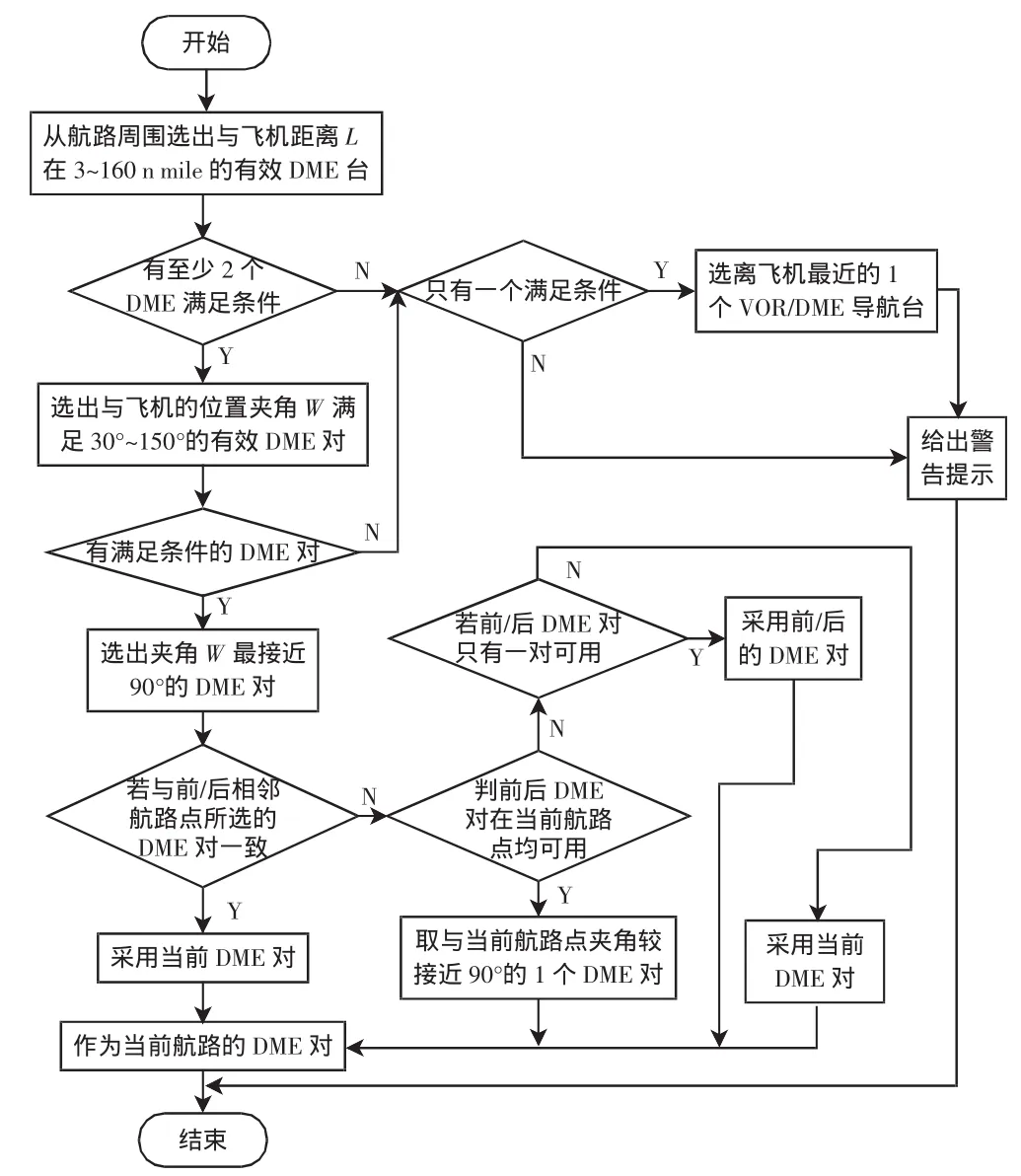
图3 导航台自动选择算法流程Fig.3 Automatic station selection algorithm flow chart

首先，先取定一个航路点为飞机当前的位置，按照DME/DME区域导航的要求，从航路周围选出到飞机的距离满足3 n mile＜L＜160 n mile的DME台，作为有效的DME台。然后从所选出的DME台中，选出有效的DME对，即2个导航台与飞机之间的夹角满足30°＜W＜150°的DME对。

以A表示飞机当前所在的位置，P表示一个DME导航台，S表示另一个DME导航台，dist（A，P）与dist（A，S）分别表示2个导航台到飞机的距离，dist（P，S）表示2个导航台之间的距离，则导航台选择原理表示为

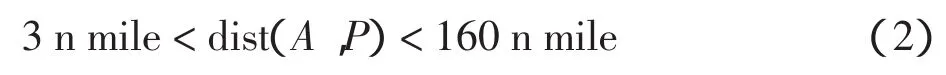
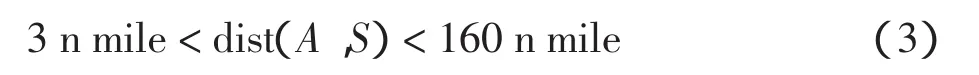
设D1=dist（A，P），D2=dist（A，S），D0=dist（P，S），根据余弦定理，可计算交角W

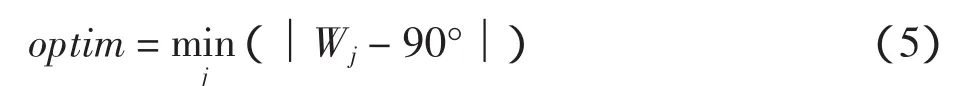
其次，若当前航路点所选的DME对与前面或者后面相邻的航路点所选的DME对一致，则采用此时所选的导航台；若当前航路点所选的DME对与前面和后面所选的DME对均不一致，即3个相邻的航路点Ai（i=1，2，3）分别选择各不相同的DME台为Pi和Si（i=1，2，3），则采用下面的方法进行改进。

由于当前航路点距离前后相邻的航路点很近，且与前后相邻航路点所选的DME对构成的夹角也较接近90°，所以若前后所选的DME对在当前航路点仍可用，即飞机当前位置仍在前后所选DME对的有效导航区域内，则继续采用前面或后面所选的导航台作为当前航路点的DME对，从而避免3个相邻航路点出现连续2次切换导航台的情况。因此，仍然按照DME/DME区域导航的要求，判断飞机的当前位置仍在前后所选DME对的有效导航区域内，即分别计算当前航路点到前后DME对的距离dist（A2，Pj）（j=1，3）和dist（A2，Sj）（j=1，3）及与前后DME对构成的夹角W是否满足条件，然后分以下3种情况判断：

1）若前后相邻的航路点所选的DME对在当前航路点均可用，如图4所示，图中星号表示的是分别3个连续航路点Ai（i=1，2，3），分别选择不同DME对（Pi，Si）（i=1，2，3），从图中可以发现中间航路点不仅在前面航路点所选DME对的有效导航区域内，也在

式中：D1和 D2分别为飞机的位置点（X，Y，H）到 2个DME台的距离；D0为2个台站之间的距离。

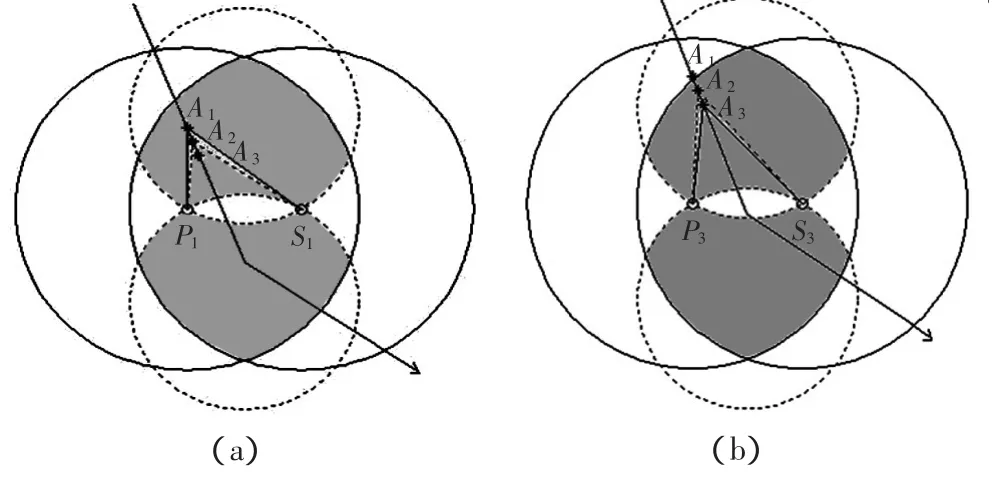
图4 前后DME/DME导航台的有效导航区域Fig.4 Effective navigation area of DME/DME front and behind WPT

利用式（4）求出满足区域导航条件的DME对与飞机连线的夹角W，然后利用下面公式可求出最接近90°的夹角，并能得到所对应的导航台后面航路点所选DME对的有效导航区域内，此时需利用式（4）计算出当前航路点与前面和后面DME对所构成的夹角，并进行比较，取夹角更接近90°的一个DME对作为当前航路点的导航台；

2）若前后相邻的航路点所选的DME对只有一对在当前航路点可用，如只有后面的DME对可用，即当前航路点只在后面航路点所选DME对的有效导航区域内，即如图4（b）中的情况，则取后面航路点的DME对作为当前航路点的导航台；

3）若前后相邻的航路点所选的DME对在当前航路点均不可用，即当前航路点既不在前面航路点所选DME对的有效导航区域内，也不在后面航路点所选DME对的有效导航区域内，则只能用原来所选的导航台。

最后，将以上改进算法应用到所有航路点，生成所有航路点的导航台数据。

3 仿真结果与分析

3.1 DME/DME区域导航选台算法仿真

本文利用Matlab建立了导航台自动选择模型，以A593航路及周围的DME导航台进行仿真实验，并将整个航路按关键的航路点分成了若干段。为了检验本文的改进算法是否能达到预期结果，可选用两段导航台切换最频繁的航路做实验。本文选用的是第10段航路和第13段航路。

为实验方便，航路周围的导航台采用数字编号的形式。实验中选取航路上第一个航路点为飞机的初始位置，得到一个航路点的可用DME对，然后应用到所有关键航路点，最后应用到航路上所有航路点，得到所有航路点的最优DME对。传统算法与本文算法的仿真结果如表1和表2所示（表中，如27/15表示该航路点所选的DME对编号分别为左27和右15）；同时，得到这两段航路改进算法前后的DME/DME导航台切换情况，对比结果如图5和图6所示。

表1 第10段航路点的DME/DME导航台选择情况对比Tab.1 DME/DME navigation selection comparision of route section#10

从表1中可以看到，当对第10段使用传统算法时，在该段航路上有7个航路点，每经过一个航路点都会切换一次DME/DME导航台；改进算法后，本段航路不仅由原来的导航台切换6次降为3次，并且没有了3个相邻航路点连续切换2次的情况。图5与之对应，从图中能更清晰地看到DME切换次数的变化，图5中（a）、（b）分别为传统算法和本文改进算法的导航台切换情况，可以发现改进算法在很大程度上提高了本段航路导航台选择的稳定性。

表2 第13段航路点的DME/DME导航台选择情况对比Tab.2 DME/DME navigation selection comparision of route section#13

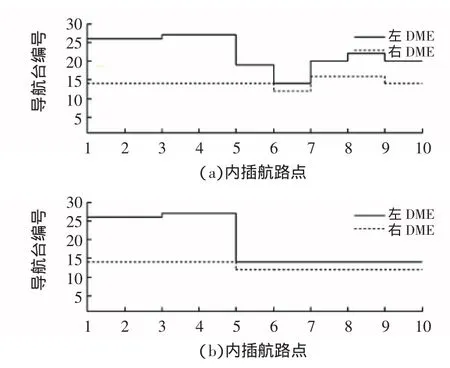
图5 第10段航路点的DME/DME切换对比Fig.5 DME/DME navigation modification comparision of route section#10

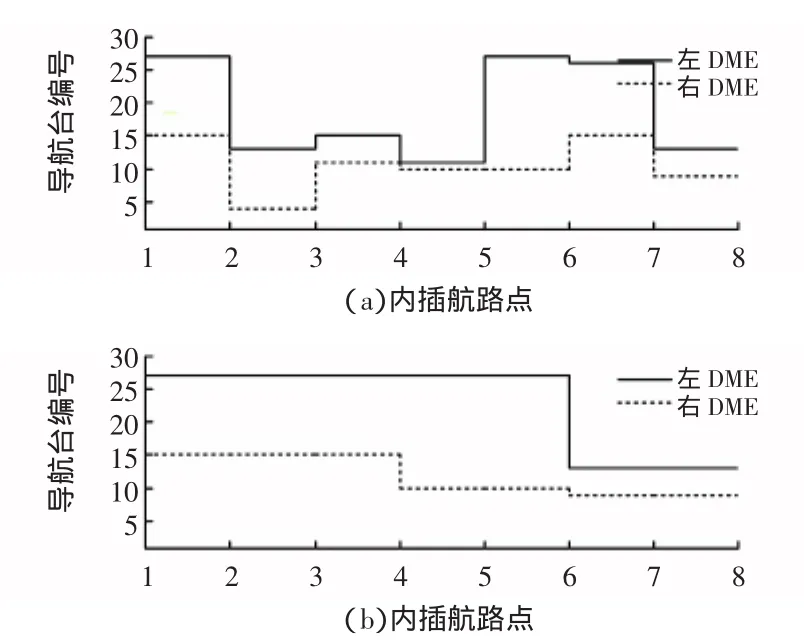
图6 第13段航路点的DME/DME切换对比Fig.6 DME/DME navigation modification comparision of route section#13

从表2中可以看到，当对第13段使用传统算法时，经过9个航路点DME/DME导航台切换6次；改进算法后，由原来切换6次降为2次，同第10段航路一样没有了3个相邻航路点连续切换2次的情况。与之对应的为图6，从中同样可以明显发现改进算法大大提高了本段航路导航台选择的稳定性。

从图7和图8中可以看到，第10段和第13段航路所显示改进算法前后导航台选择结果分别与表1和表2的数据相对应。从图7和图8中可以发现，改进算法前DME台与航路点的连线只有一次或不连续的两三次，也就是几乎每经过一个航路点，就会选择新的DME导航台，说明传统选台算法导航台切换比较频繁；而改进算法后，可以发现导航台选择有规律可循，1个DME导航台周围会出现与航路点连续连线的情况，表明在某一段航路的航路点会持续选用此导航台，证明改进算法可以在一定程度上减少导航台切换的次数。

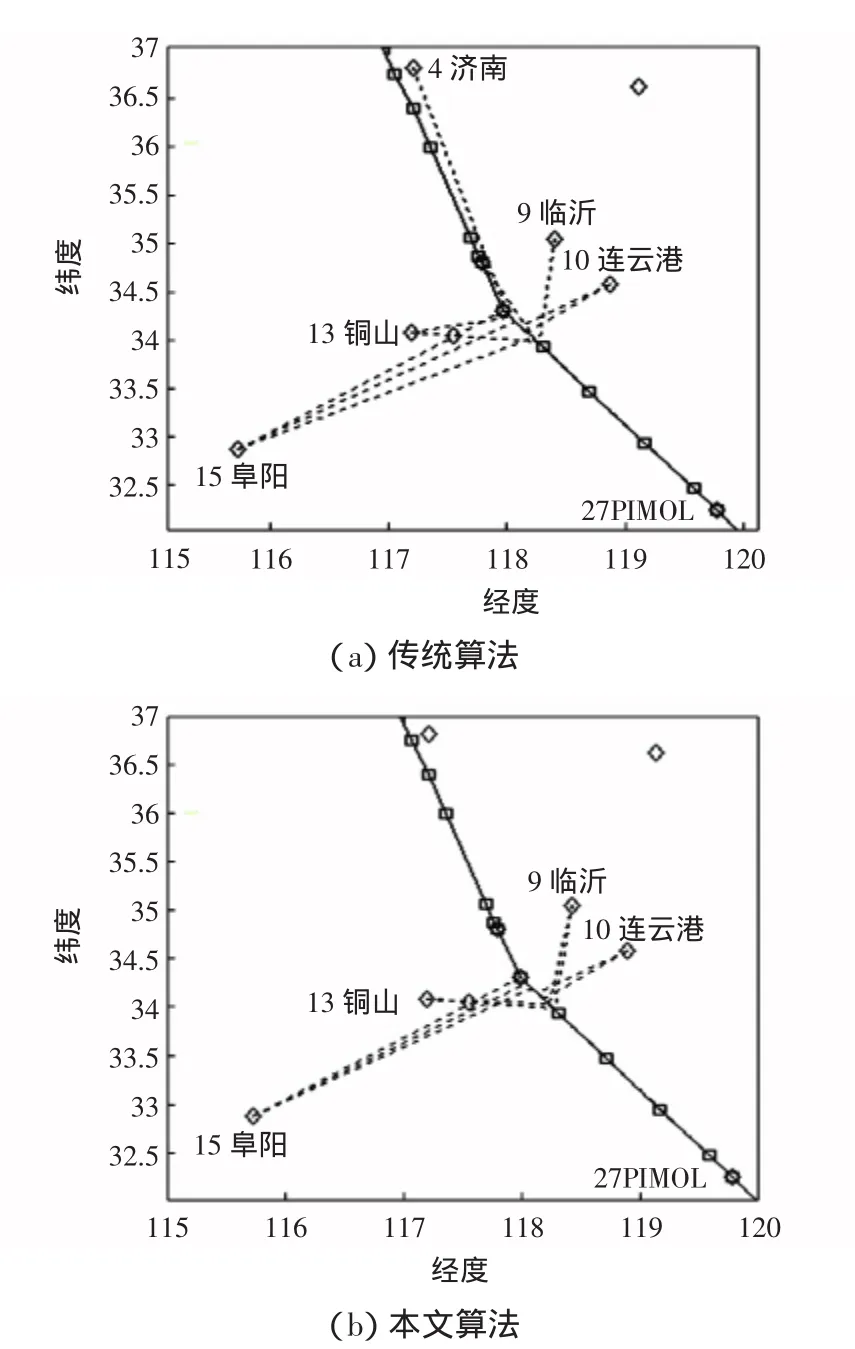
图7 第10段航路点DME/DME导航台选择情况对比图Fig.7 DME/DME navigation selection comparision diagram of route section#10

最后，将改进算法应用到整个航路，得到所有航路点的DME/DME导航台选择情况，如图9所示。从图9可以发现在整个航路出现较多的1个DME导航台周围连续连线的情况，这种情况出现得越多，说明在航路上导航台切换的次数越少，进一步证实了改进算法的有效性。

3.2 DME/DME区域导航选台算法的性能评估

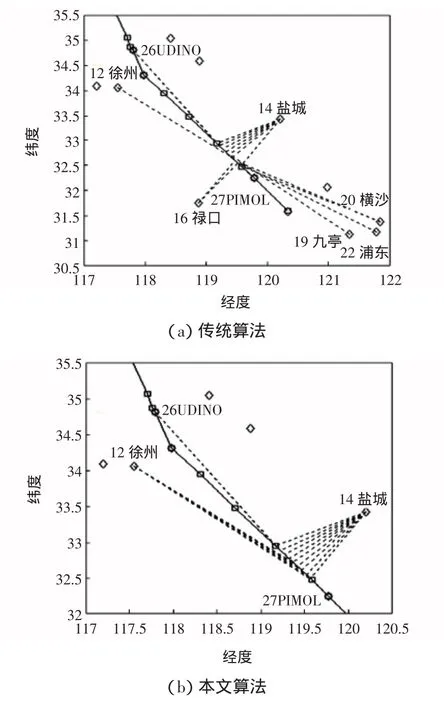
图8 第13段航路点DME/DME导航台选择情况对比图Fig.8 DME/DME navigation selection comparision diagram of route section#13

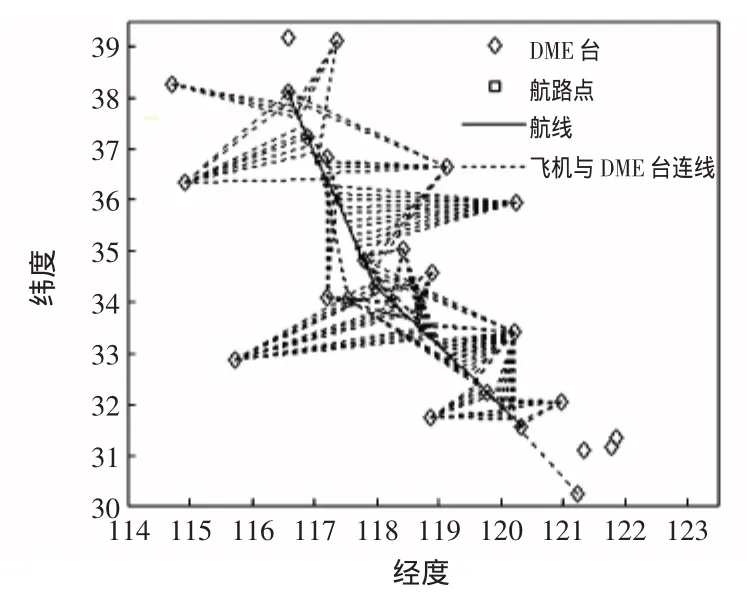
图9 所有航路点DME/DME导航台选择情况Fig.9 DME/DME navigation options of all WPTs

为了验证本文算法是否满足DME/DME区域导航的性能要求，下面根据PBN Manual中的要求进行计算。根据其中规定，当使用满足DME/DME区域导航的DME导航台时，并且没有任何其他的DME导航台满足区域导航的要求，则要求在95%的飞行时间内，位置估计误差（position estimation error，PEE）必须满足

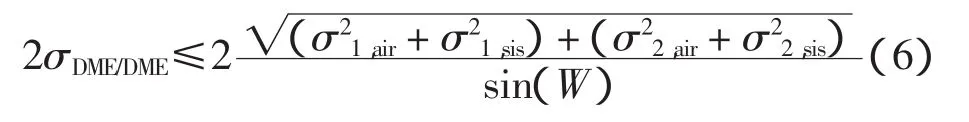
其中

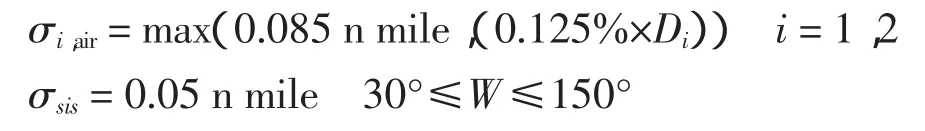
同时根据RNAV1的要求，实现DME/DME区域导航要求在95%的飞行时间内，总系统误差（TSE，total system error）必须小于等于±1 n mile。TSE包括导航系统误差（navigation system error，NSE）和飞行技术误差（flight technical error，FTE），因此，TSE 由导航系统误差和飞行技术误差共同决定。其中导航系统误差包括位置估计误差、航路定义误差和显示误差，对于航路定义误差及显示误差这里可以暂不考虑。目前FTE一般可达到0.5 n mile，由于这两个误差是独立的，所以TSE可以根据下面公式来计算

因此，总的误差分配给NSE最大误差可达到0.866 n mile，即按照式（6）计算出的结果必须是小于0.866 n mile[12]。

由式（6）计算位置估计误差PEE值，验证是否满足小于0.866 n mile的要求。

由图10可以看到不论传统算法还是本文算法所选导航台的位置估计误差PEE值都小于0.866 n mile，验证了本文算法是满足DME/DME区域导航的性能要求的。

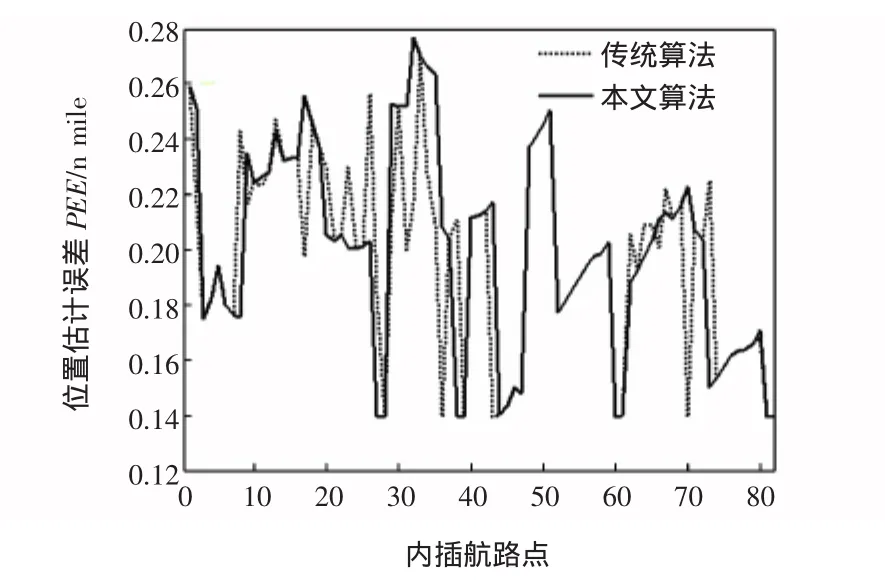
图10 位置估计误差PEE值的比较Fig.10 Comparison of PEE values

综合以上仿真结果，本文改进算法可保证选台的有效性，同时避免了导航台过于频繁的切换，即在一定程度上保证了可靠性，并且满足DME/DME区域导航的性能要求。

4 结语

本文根据DME/DME区域导航在航路阶段的要求，提出了一种区域导航航路阶段的避免频繁切换的DME/DME导航台选择算法，在地面导航台分布密集地区应用本文算法，可以在一定程度上避免导航台的频繁切换。本文以A593航路为例进行了仿真实验，利用Matlab建立了导航台自动选择模型，最后对所选DME/DME的区域导航性能进行了评估。仿真结果表明：根据飞机当前的经、纬度及航路周围的DME导航台分布，该算法能够自动选择一对更加合理的导航台，并且满足DME/DME区域导航的性能要求，提高了选台的稳定性，使算法更有实际应用的价值。

[1]施 健.满足区域导航性能的陆基导航技术研究[D].南京：南京航空航天大学，2010.

[2]隋 东，王 炜，左 凌.基于DME/DME的区域导航航路导航性能评估方法[J].交通运输系统工程与信息，2006，6（4）：24-28.

[3]GERHARD E BERZ，JOCHEN BREDEMEYER.Qualifying DME for RNAV Use[C]//15th International Flight Inspection Symposium，USA，2008.

[4]EUIHO KIM.Investigation of APNT Optimized DME/DME Network Using Current State-of-the-Art DMEs[C]//Position Location and Navigation Symposium，2012 IEEE/ION，Myrtle Beach，2012：146-157.

[5]石宝峰，程 朋，程 农.区域导航进近阶段导航台选择模型与仿真[J].系统仿真学报，2011，23（10）：2039-2045.

[6]JACOTOT，GREGOIRE.Method Automatically Selecting Radio Navigation Beacons：US，7652621[P].2010-01-26.

[7]赵 健.基于性能导航的发展[J].空中交通管理，2006（11）：23-26.

[8]Federal Aviation Administration.United States Standard Flight Inspection Manual[S].Federal Aviation Administration，2005.

[9]RAWLINGS R C.The flight assessment and applications of DME/DME[J].Journal of Navigation，1981，34（1）：103-119.

[10]黄金明，王立文，田 静.飞行模拟器进程无线电导航系统建模与仿真[J].计算机仿真，2007，24（2）：282-285.

[11]GERHARD E BERZ，JOCHEN BREDEMEYER，VALERIU VITAN，et al.Calibrating DME Coverage Predictions with Flight Inspection Measurements[C]//16th International Flight Inspection Symposium，Beijing，2010：105-115.

[12]SHI DONGWEI，LU YONGDONG.Method of Signal Assesment and Flight Inspection for DME/DME RNAV[C]//16th International Flight Inspection Symposium，Beijing，2010：199-205.