基于遗传算法的虚拟维修环境布局规划研究

张忠华，耿 宏

（1.中国东方航空股份有限公司机务培训中心，上海 200335；2.中国民航大学航空自动化学院，天津 300300）

目前关于虚拟维修的研究主要集中在虚拟维修过程建模和虚拟维修场景管理两个方面。在场景管理中，当部件进行拆装时，特别是对于航空发动机这类复杂部件的拆装，必须考虑拆装后大量零部件的摆放问题，即零部件在场景中的布局问题。为提高虚拟维修环境管理效率，对拆装后产生的大量零部件做合理的布局规划非常必要。文献[1]中提出了一种遗传算法和人机交互结合的方法解决布局问题[1]，从三维空间到二维平面的简化中使用人机交互的方法来确定各个二维面；然而人机互动需要很高的硬件支持，在简单虚拟维修条件下实用性不强。文献[2]直接进行三维空间的布局[2]，从随机布局开始，利用改进编码的遗传算法得到布局，由于布局是基于三维的，需要考虑空间中3个面的情况，处理过程更加复杂。

基于此，文中将零部件模型化处理，为其包络外接圆柱体，同时应用层次划分将复杂的三维空间布局问题转化为多个二维平面布局处理。二维布局应尽可能减少拆装后组件的移动距离，缩短维修培训时间，提高效率，此处采用基于遗传算法的布局优化。

1 虚拟维修环境整体布局规划

维修环境中的零部件总体布局规划如图1所示。首先将不规则、复杂的待布局零部件模型化为简单的外包圆柱体；为了简化复杂的三维布局问题，此处建立一个部件信息库，存储各零部件的属性特征。层次划分利用其中的一些显性属性将各组件分配到不同的二维平面，处理流程如图2所示。三维空间布局问题随即转化为多个二维平面的布局问题；最后对二维布局采用遗传算法进行优化，得到虚拟拆装环境布局结果。

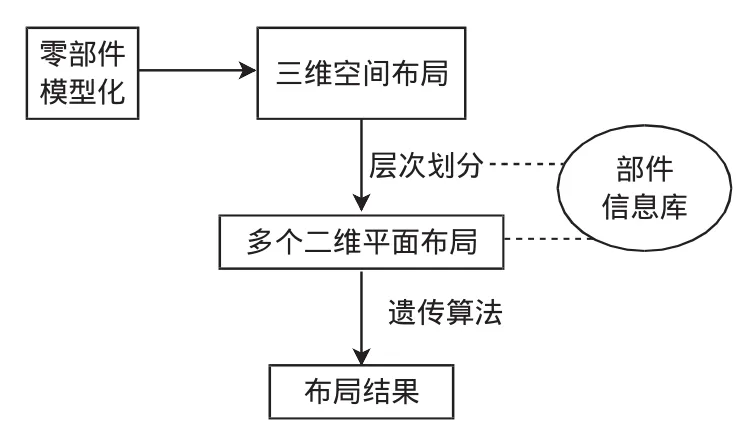
图1 虚拟维修环境布局规划整体框架Fig.1 Virtual maintenance environment overall layout planning framework

图2 虚拟环境空间规划Fig.2 Virtual environment spatial planning

部件信息库包含物理层和几何层两部分。物理层主要描述零部件的物理属性，如部件名称、拆装层次、与其他部件的结合关系等物理信息。几何层主要描述零部件的具体几何参数，如体积、质量、质心等几何信息。

三维布局转化为多个二维布局是通过层次划分完成的。层次划分主要利用拆装顺序、安装平面以及部件相似属性来进行二维平面的划分。拆装顺序在信息库的物理层中可以找到。结合组件的性能约束条件、拆装层次、部件属性关系，对拆装后的组件进行合理分类，给每个安装面或属性相似的零部件分配一个二维平面，如 P1，P2，…，Pn，使得组件布局更具层次感；以组件拆装过程中的先后顺序为依据，平面在部件的上下排列（最先拆装的零部件组成的平面距待拆装部件最远），同时规定平面上布局物排列形状接近圆形，可最大化地减少零部件的移动距离，提高虚拟维修效率。

2 二维布局数学模型

将组件模型简化为大小不一的圆柱体，规划到各平面后，以圆柱体高为平面距上一级高度，在平面Pj上（j=1，2，…，n）对 n 个圆形作布局。

在n个圆形中，第i个圆形Ri的半径为ri，质量为mi（从部件信息库中获取），i∈I={1，2，…，n}。假定模型中圆形的质心与重心重合。平面Pj的圆心为坐标原点O=（0，0），圆形Ri的位置用（xi，yi）表示，其中xi、yi分别表示第i个圆的圆心在轴x、y方向的坐标值，如图3所示。

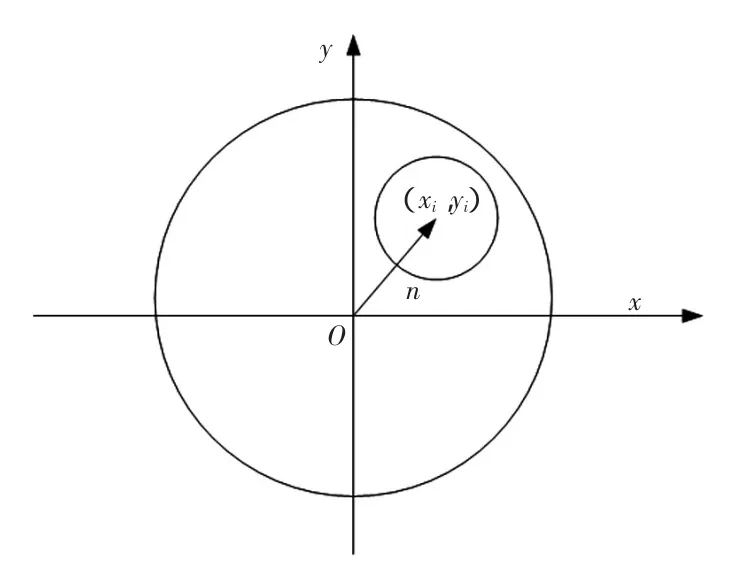
图3 最大距离圆形布局图Fig.3 Maximum distance planning

针对平面上的布局优化问题建立如下约束条件：

1）几何约束

布局问题中最基本的约束条件，要求布局物在几何上没有相互覆盖（嵌入）[3]，在这里即是圆形间不发生干涉，约束为

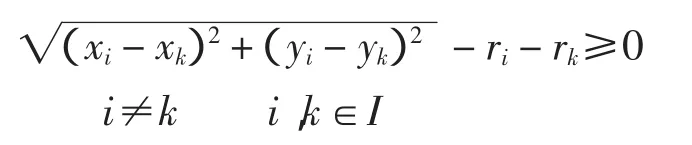
其中：（xi，yi）、ri分别为圆形Ri的圆心位置及半径。

2）平衡性能约束

为使虚拟效果更有真实感，引入平衡约束，严格要求每个平面上的平衡量δ为0，即将平面Pj上所有布局物构成的系统质心移动到待拆装部件的中心线上即可。平移后的质心为

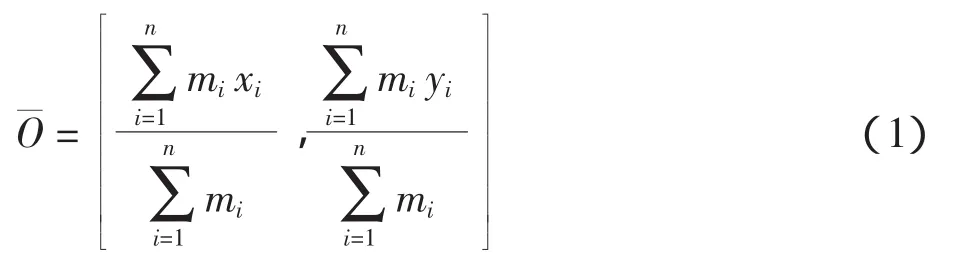
3）优化目标——包络半径最小

布局优化要求该平面上所有布局物组成的包络圆最小[4]。由平衡性能约束条件可知，最小包络半径r可定义为n个圆形的最远点到达平面中心的最长距离。此处包络半径函数用D（，R）表示

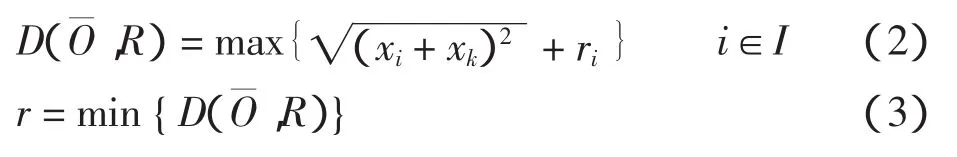
3 基于遗传算法的布局优化

遗传算法由Holland于1975年首次提出，是一种模拟生物界自然选择和遗传变异的机制来求解复杂问题的随机搜索和优化方法，通过选择、交叉、变异等操作来实现[5]。实践表明，遗传算法易产生早熟现象、计算时间较长，此处在基本遗传算法的基础上对初始解和控制参数进行了调整，应用于布局优化中[6]。

3.1 初始解的产生

假定布局物的集合为Ii（i=0，1，…，n），则I0表示还未开始布局的集合。通过布局集合中的任意圆形Ri（i=0，1，…，n）确定其所属集合的有效布局空间。每次待布物的布置选择，只在其有效解空间中选择随机解[7]。

1）取待布物 Ri；

2）确定Ri的有效解空间：

a.在平面Pj中任意选择xi；

b.做直线 X=xi；

c.判断当前解是否与现有解冲突，处理流程如图4所示。其中ri为圆形Ri的半径，xi-1、ri-1为Ri前一个布局圆形的参数；

d.对于冲突解，将其存储至禁止区域集合中，避免多次冲突。同时为Ri重新选择适用区域；

e.同样的方法选择yi坐标。

3）随机选择个体解，直至完成该平面上所有圆形的布局。

3.2 算法中基本参数的选择

3.2.1 编码策略

遗传算法的传统编码最初均采用二进制，后来又有整形、实数等编码形式。一般求解中会使用二进制符号串来表示群体中的个体。在布局问题中，为了更方便适应度函数的表示及求解，此处使用基于实际位置坐标形式的实数编码，即染色体表示为：{（x1，y1），（x2，y2），…，（xn，yn）}。其中，xn和 yn分别表示第 n 个布置圆形Rn的实际位置。

3.2.2 适应度函数

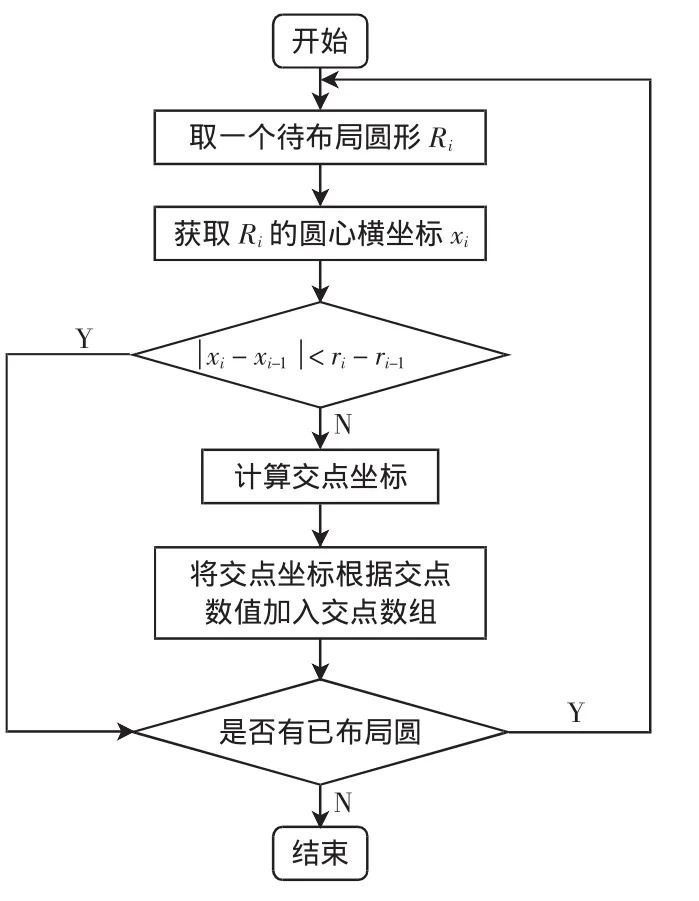
图4 确定冲突解流程图Fig.4 Definite conflict solution flow chart

此处采用实数编码，可直接将目标函数作为适应度函数，从而大大降低个体适应度评价的复杂度。这样就可直接用个体的解作为评价个体适应度的度量指标，保证适应度值较低的个体也会以概率遗传。从而在适应度值低的情况下保证群体的多样性，在一定程度上避免局部收敛。当群体的适应值较高时，又有利于种群的整体收敛。

3.2.3 控制参数

控制参数包括变异概率和交叉概率，与迭代次数有关。同时，与当前代的分布状态有关，与个体的表现也有关，每一层的二维布局优化中参数值的选取将视情况选择。

3.2.4 选择算子

本文采用转轮盘方式进行个体选择[8]。首先计算个体的相对适应值其中xi表示Ri确定位置时的圆心横坐标，Σxi表示所有可能横坐标值的和。再根据选择概率随机选择个体，从而得到父本。此处通过一个随机数δ完成，δ∈[0，1]。若q0+q1+… +qi-1＜δ≤q0+q1+…+qi，则第i个个体被选择到下父本中。

3.2.5 交叉算子和变异

交叉和变异可保证遗传算法在进化过程中样本的多样性，从而使问题具有全局寻优的意义[9]。本文算法中，当被布置个体的适应度较低时，以满足转动惯量最小的原则，对原布置微调，此操作视为交叉。反之，对布置物重新布置，这种大范围的调动视为变异，从而使其作为一种搜索算子进行全局的解搜索。

3.2.6 算法步骤

1）设置群体代数t=0，按照初始解规则生成规模为N的初始群体；

2）对初始种群进行适应度评价；

3）进行复制、交叉和变异操作，生成新的子代群体；

4）评价新一代群体的适应度，并记录该代群体中的最优个体；

5）按照收敛准则检验，若满足，则转6）；否则，令t=t+1，转至步骤 3）；

6）结束迭代，输出最优个体，并解码出最终结果。

4 实例分析

航空发动机内的组件拆装一直是飞机维修过程中的复杂对象之一，其拆装后包含的零部件多达上千个。下面对某航空发动机高压压气机装配零部件做层次划分，在前机匣装配层、轮盘转子装配层、高压压气机装配层、轮盘装配层这4个二维层上进行布局。运用基于遗传算法的布局方法对某个二维层作零部件布局优化，模型简化后的圆形参数如表1所示。遗传算法的参数取值如下：编码串长度15，群体大小200；终止代数100，交叉概率0.6，变异概率0.3。最终布局如图5所示。

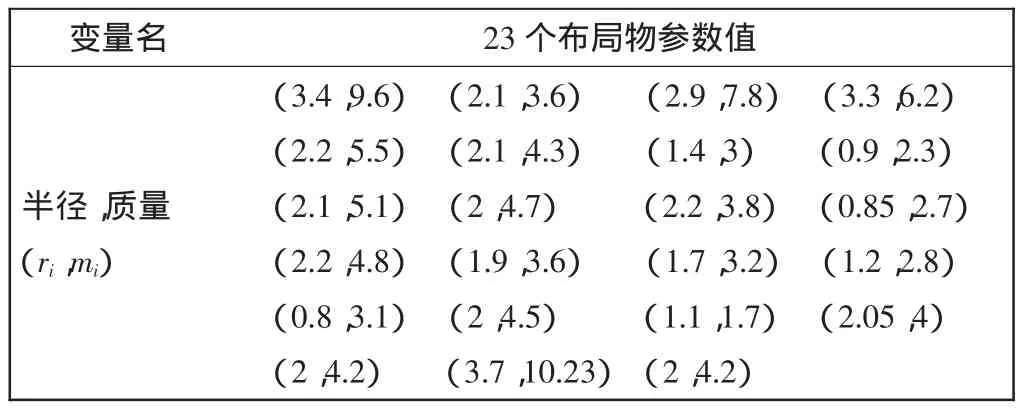
表1 二维层上圆形模型参数Tab.1 Circular model parameter of two-dimensional layout

5 结语

本文针对虚拟维修环境的三维布局，利用层次划分简化为多个二维平面布局问题，同时在二维布局中采用遗传算法进行优化，提出了一种虚拟维修零部件布局的可行性方法。本文将组件均简化为其包络圆柱体，然而组件形状其实是各异的，设计针对任意形状的布局方法，更精确地达到布局最优化是需要进一步研究的内容，同时，采用的遗传算法在参数选择上可以加入自适应算法，提高算法的有效性。

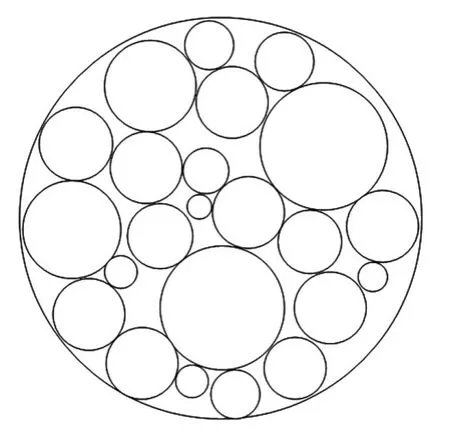
图5 二维层上圆形模型布局优化结果Fig.5 Circular model layout optimization results two-dimensional layout

[1]何良莉，魏发远，王峰军.虚拟布局/装配环境下的人机交互技术研究[J].机械设计，2010（5）：86-89.

[2]张 刚，邓克文，李火生，等.复杂结构产品虚拟布局与装配设计系统研究[J].计算机集成制造系统，2008，14（2）：209-214.

[3]钱志勤，滕弘飞.人机交互的遗传算法及其在约束布局优化中的应用[J].计算机学报，2001，24（5）：553-559.

[4]季 关，肖人彬.基于蚁群算法的带平衡约束矩形布局问题的启发式求解[J].计算机应用，2010，30（11）：2898-2901.

[5]HOLLAND J H.Adaptation in natural and artificial systems：An Introductory Analysis with Applications to Biology，Control，and Artificial Intelligence[M].Oxford：U Michigan Press，1975.

[6]SCHNECKE V，VORNBERGER O.Hybrid genetic algorithms for constrained placement problems[J].IEEE Transactions on Evolutionary Computation，1997，1（4）：266-277.

[7]李亚洲，郑晓军，张 强，等.基于改进初始解的遗传算法的布局设计方法[J].计算机工程与应用，2013，49（8）：245-248.

[8]于 洋，查建中.基于学习的遗传算法及其在布局中的应用[J].计算机学报，2001，24（12）：1242-1249.

[9]张 刚，殷国富，邓克文，等.解空间编码遗传算法在三维布局中的应用[J].中国机械工程，2006，17（1）：79-83.