基于复杂度加权的Voronoi图扇区边界划分研究

王莉莉 ，胡 婧 ，高 峥

（1.中国民航大学空中交通管理学院，天津 300300；2.民航天津空管分局，天津 300300）

空域管理部门通常将空域划分为若干个扇区，每个扇区设立一个管制席位，进行空中交通的指挥和协调工作。近年来，随着民航业的迅猛发展以及飞行运行总架次的日益增长，空中交通管制员在其管辖范围内指挥的飞机数量越来越多，管制员的工作负荷越来越大，致使空中交通管制系统面临着越来越严峻的挑战，对飞行安全带来不利影响。有些扇区的管制员工作负荷量较少，而有些扇区的管制员工作负荷量却很大，扇区的管制员工作负荷不均衡的原因在于目前扇区的划分缺乏科学合理的规划，因此，如何在划分扇区时进行综合优化，确保空域划分的科学、合理和有效，成为民航空中交通管制领域不少学者研究关注的一个重要课题。

国内外很多研究人员对最优扇区划分问题进行了研究：首先，国际民航组织（ICAO）颁布了“DORATASK”和“MBB”管制员评估法，此类方法是通过对管制员工作负荷的分类以及一定的时间间隔观察管制员的活动来确定工作负荷[1-2]；Huy Trandac等通过建立平面的Voronoi多边形和采用启发式优化算法，确定了二维扇区划分结果[3]；2003年，韩松臣、张明提出了以导航台、航线交叉点和空域边界上的航路点为节点的蜕变的Voronoi图，应用模拟退火算法获得优化的扇区边界线[4-6]；2009年，中国民航大学的戴福青提出了基于Power图和空中交通复杂度的多机场划设方法，分别对多机场地区终端区分高低两层扇区进行研究，以扇区结构特征为约束条件，采用遍历搜索算法搜索寻优找到最终优化的扇区[7-8]。

本文提出考虑导航台、航线交叉点和空域边界上的航路点的分布，采用加权Voronoi图将空域划分为有限单元，与普通Voronoi图不同，在加入扇区单元航迹数目以及导航台影响能力不同而设置不同权值的基础上，根据各有限单元的工作负荷，建立了扇区优化模型，使扇区单元组合更加合理；提出统计复杂度值时，添加考虑飞行速度的变化以及不同天气情况等因素对扇区规划的影响，使复杂度统计值更加完善，最后采用生长算法对空域中的加权Voronoi多边形进行优化组合，以加快计算速度。

1 加权Voronoi图

一般Voronoi图是假设除了生成元的位置外，其他都是相同的；而空管实际运行情况则不然，比如在一些空域扇区单元内航迹较多，而一些扇区单元内航迹很少，如果还设置相同的权值进行划分是不合理的。因此由不同的权值反映不同生成元的性质更加合适，更加贴近实际情况，所以引入加权Voronoi图。

定义设生成元集合S={p1，…，pn}⊂R2（2≤n≤∞），权值集合为 W={w1，…，wn}，wi为生成元 pi的权值（i=1，2，…，n），则加权 Voronoi图定义为

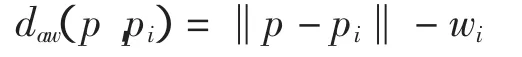
式中：daw（p，pi）为加权距离。加权距离下的pi控制区域记作V（pi）=∩Dom（pi，pj），其中Dom（pi，pj）={p|daw（p，pi）＜daw（p，pj）}，i≠j；Vorw（P，dw，R2）={V（p1），…，V（pn）}为带权集{w1，…，wn}的集合 P 生成的加权 Voronoi图，集合Vor（Pi）定义成与Pi关联的加权Voronoi域。

图1为厦门管制区空域结构，图2为基于此空域结构生成的Voronoi图，图3为加权后的Voronoi图。图2与图3相比而言，如果不加入一定的权重值，空域边界上的导航台或位置点作为生成元生成的Voronoi区域较小，不符合飞越该空域边界所需负荷较大的特点。图3中的黑点代表生成元，序号1、2、3等为扇区单元序号，共分为12个扇区单元；从图1中的空域结构图可以看出航迹，导航台的覆盖范围和使用情况不同，以DO导航台为生成元为例，背台和向台飞行的航迹较多，航路结构复杂，其权重值应较大。因此，综合上述因素为其赋值不同的权值wi分别代表它们的不同影响能力。本文在加入权重值基础上使得随后的实例二维平面空域扇区最优边界的寻找更加符合实际。

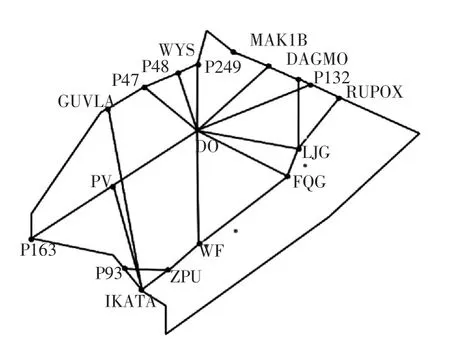
图1 厦门管制空域结构图Fig.1 Structure of Xiamen controlled airspace

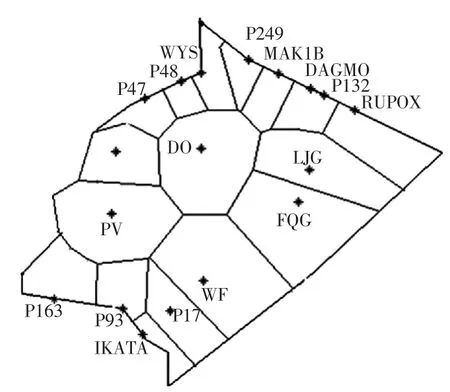
图2 Voronoi图Fig.2 Voronoi diagram

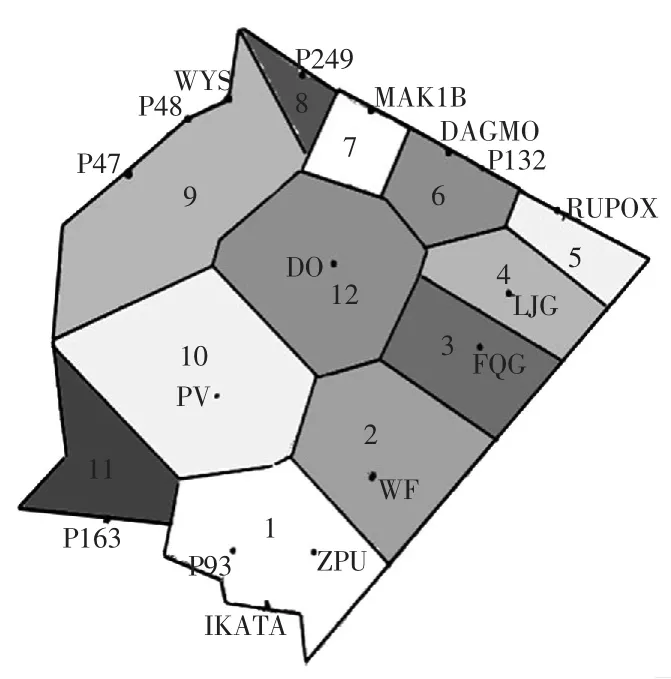
图3 加权Voronoi图Fig.3 Weighted Voronoi diagram

2 扇区容量的确定

2.1 空中交通复杂度模型

为了精确量化管制员所面临的并要解决的交通状况的困难程度，以往大多都是以统计管制员负荷或者雷达轨迹搜索到的详尽的飞行数据资料的方法进行研究，而目前以空中交通复杂度进行研究更好。其优势在于复杂度模型避免了早期直接的管制员工作负荷模型中带来的主观工作负荷难以测量的弱点，直接利用航空器速度、航向等交通流内部属性对空域状态的复杂程度进行客观的描述，能较好地兼顾扇区空域资源的灵活使用和管制员工作负荷影响，实现扇区资源的有效利用。

2.1.1 空中交通复杂度的数据统计

本文根据影响空中交通复杂度的因素，结合扇区的结构特征建立了空中交通复杂度模型，尝试使用结合扇区飞机流量的空中交通复杂度标准来作为评估标准，间接反映扇区容量。复杂度只限于交通状况本身的特性，与以往管制员工作负荷的统计不同，避免了管制员指挥飞行器时的个体差异，具有客观性。

扇区单元复杂度用以下4个元素进行衡量：

1）飞行速度的变化：航空器以不同航速在飞行时会造成管制员的工作强度。如在程序飞行中当前后航空器之间的飞行速度相差大于80 km/h时，飞行间隔为2 min，而如果速度小的航空器在前，速度大的在后同高度飞行时，应保证在到达着陆机场上空或者改变高度层以前要有10 min的纵向间隔，这给管制员造成的不同的工作难度，可表示为

式中：ws为飞行速度权系数；Ti，Tj为不同航速的航空器通过扇区单元的时间；T为航空器平均穿越扇区单元所用的时间。

2）飞行状态的变化：飞行状态一般有起飞、降落和飞越，管制员对其中任何单一的状态调配都比它们的混合状态简单；因为调配所发指令数不同，工作强度不一样，可表示为

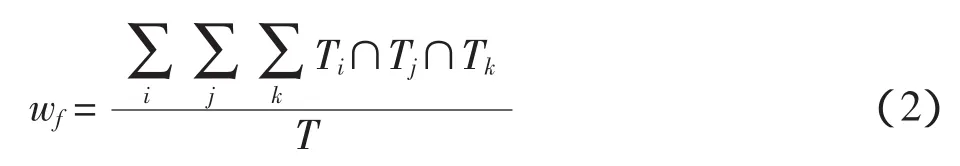
式中：wf为飞行状态权系数；Ti，Tj，Tk为航空器在 3 种飞行状态下通过扇区单元所需要的时间；T为航空器平均穿越扇区单元所用的时间；Ti∩Tj∩Tk表示航空器在混合状态下穿越扇区所用时间。

3）飞机类型的不同[8]：调度同一类型的飞机要比调度不同类型飞机容易很多。所以每个扇区单元的复杂度值要考虑飞机类型权重系数wap。根据尾流间隔把飞机分为重型机、中型机和轻型机，可表示为

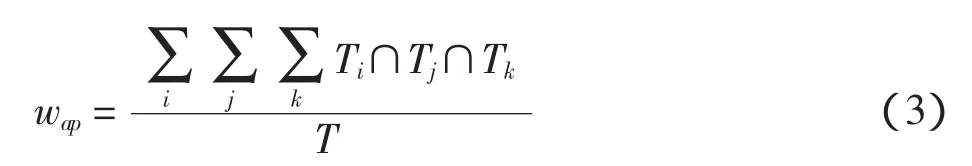
式中：Ti，Tj，Tk为3种航空器在同一时段内穿越扇区所需时间；T为航空器平均穿越扇区单元所用的时间。

4）天气情况的不同：气象条件的不同会给管制员在调配工作方面带来不同的难度。天气越恶劣，航空器在通过一片扇区时管制员需要投入工作的时间和精力越多。所以空中交通复杂度要考虑天气情况权重系数。设天气情况权重系数为ww。其中恶劣天气情况有颠簸、积冰、雷暴、风切变等，可表示为

式中：Ti为不同恶劣天气情况下航空器通过扇区所用时间；T为航空器平均穿越扇区单元所用的时间。

2.1.2 空中交通复杂度计算

以导航台为中心的扇区单元的空中交通复杂度值为

据上述数据统计，计算出在一天24小时内厦门管制底层空域各扇区单元空中交通复杂度，如图4所示。图中2号扇区靠近厦门进近，所以复杂度值大；3号、4号扇区单元复杂度值也较大，因为靠近福州进近；5号、6号、7号、8号和11号扇区单元远离进近所以复杂度值较小；靠近武夷山进近的9、10号扇区复杂度值也较大；1、12号扇区因为航路网结构复杂，所以复杂度值也较大。

2.1.3 扇区单元管制员工作负荷

式中：Wload为扇区单元管制员工作负荷；TC为空中交通复杂度值；N为通过扇区单元的航空器架次数。

以扇区12单元为例，在11点到14点的高峰时段内，空中交通复杂度值TC为1.3，而在这个高峰时期该扇区单元的流量N为18，工作负荷Wload为23.4。

根据空中交通复杂度值的计算间接算出厦门管制底层空域各扇区单元管制员工作负荷，如图5所示。

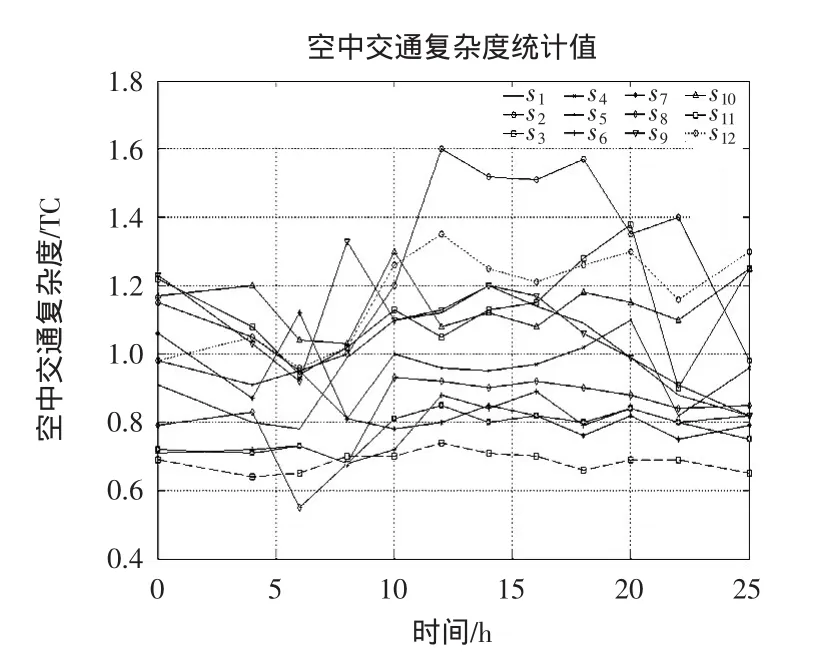
图4 扇区单元各小时段内的空中交通复杂度值Fig.4 Air traffic complexity of sector unit in each period

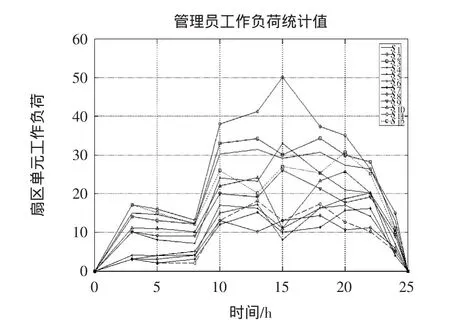
图5 各扇区单元的管制员平均每小时管制负荷Fig.5 Average hourly controller workload in each sector unit

2.2 扇区边界寻找算法

通过上述空中交通复杂度模型的建立以及扇区单元管制员工作负荷的计算，为了加快得到最优的扇区边界，针对本组合问题，结合生长算法的优点，所以提出一种先采用生长算法得到信息素，并调用该信息素进行优化求解的方式来得到全局最优解。这样大大加快了求解速度。下面以划分为2个扇区为例，给出流程图如图6所示。

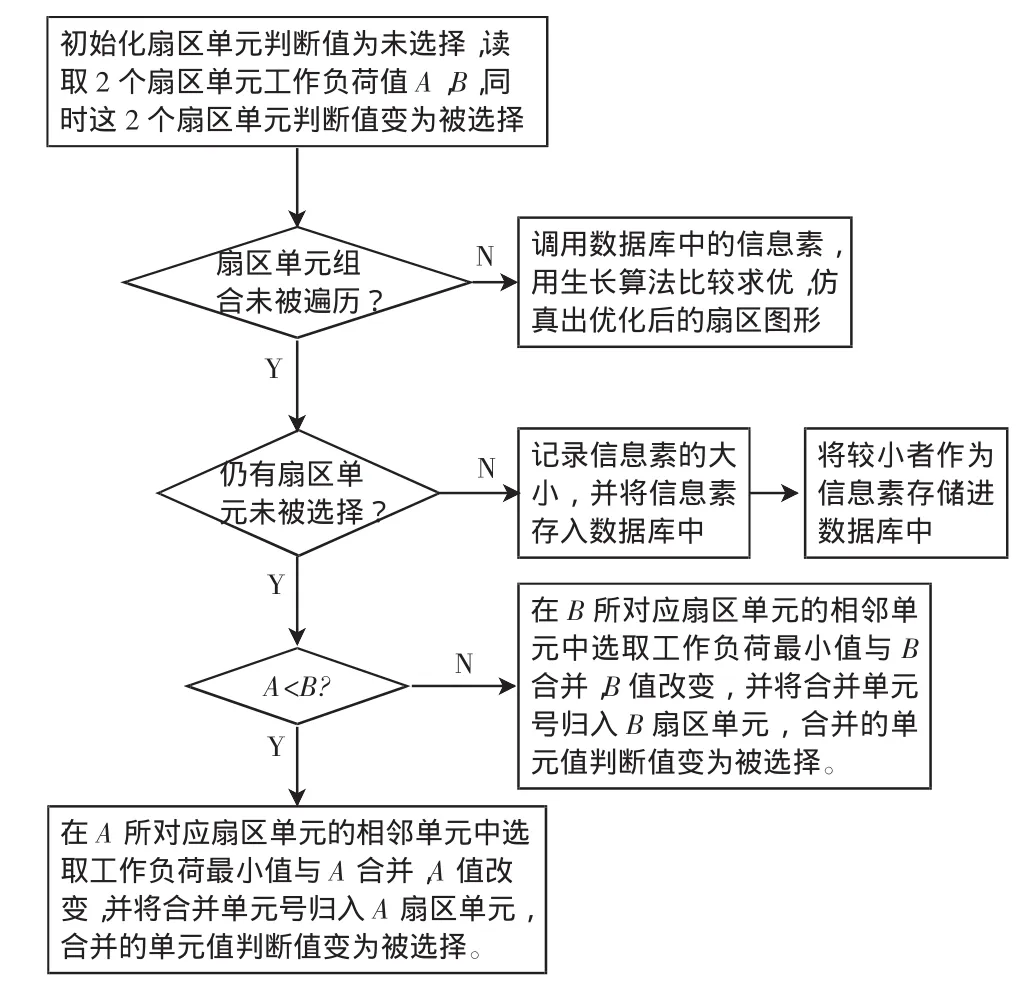
图6 生长算法流程图Fig.6 Flowchart of growing algorithm

3 实例分析

通过上述管制员工作负荷统计得到，繁忙时段11：00—14：00内总管制负荷较高，为厦门空管站使新划分的扇区能应对未来流量增加一倍的要求，重新对底层空域进行扇区划分：

1）以目前的管制空域结构为基础，拆除原始低层空域中扇区的边界线和该边界线上用于扇区移交的报告点。得到未划设扇区的原始空域结构，如图7粗黑线所示；

2）以原始空域图中的航路点和航路交叉点为节点建立的Voronoi图形成的扇区边界较为参差不齐，因为未加入权值的扇区单元生成是随机的，不具有客观合理性，所以较为多边形化。加入了生成元对应扇区单元的权值后扇区边界较为圆滑，满足扇区边界的约束条件。加权后的Voronoi图，如图7细黑线所示；

3）计算每一个扇区单元的管制工作负荷，获取有限元的相邻列表。再利用生长算法得到划分后的扇区仿真，如图8所示，分为3个扇区。

图7 管制空域结构图Fig.7 Controlled airspace structure

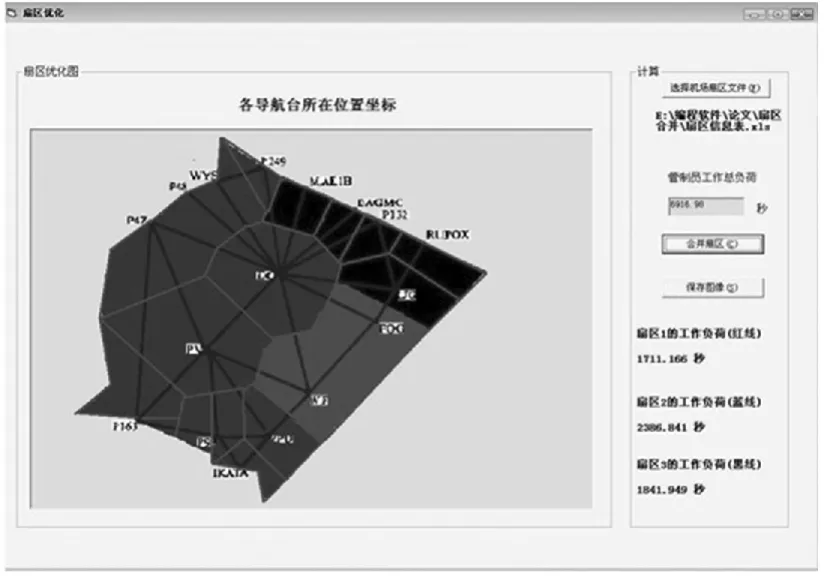
图8 仿真后的扇区优化图Fig.8 Optimization sector plot after simulation

4 结语

本文分析了影响扇区管制员工作负荷的复杂度因素，并建立了空中交通复杂度模型来间接计算扇区容量，避免了主观分析法的不全面性。通过算例仿真分析验证了其可行性：①利用加权Voronoi图所画出的扇区考虑到了工作负荷的影响，使分块后得到的扇区比普通的Voronoi图更精准，同时满足方便扇区协调移交约束条件。②利用生长算法在连续性约束下可更快速准确的进行仿真计算，此算法计算量比较小，较快的得到扇区边界。

本文的研究还有很多不足之处，一方面如何在复杂度计算中综合众多的因素来得到更准确的权值；另一方面对未来空域复杂度的变化没有做出一定的预测判断，这些都值得进一步的研究。

[1]PAWLAK W S，GOEL V，ROTHENBERG D B，et al.Comparision of Algorithms for the Dynamic Resectorization of Airspace[C]//AIAA Guidance Navigation，and Control Conference and Exhibit.Reston，VA：American Institute of Aeronautics and Astronautics，1998：67-74.

[2]LAUDEMAN I V，SHELDEN S G，BRANSTROM R，et al.Dynamic density：An Air Traffic Management Metric，NASA-T M-1998-112226[R].Moffett Field，CA：NASA Ames Research Center，1998.

[3]HUY TRANDAC，DUONG V.Optimized Sectorization of Airspace with Constraints[C]//In 5th Eurocontrol/FAA ATM R & D Seminar，2003：23-27.

[4]韩松臣，胡明华，蒋 兵.扇区容量与管制员工作负荷的关系研究[J].空中交通管理，2000（6）：42-45.

[5]韩松臣，张 明.依据管制工作负荷的扇区优化新方法[J].南京航空航天大学学报，2004，36（1）：91-96.

[6]张 明.管制扇区的最优划分方法研究[J].南京航空航天大学学报，2004，（3）：308-312.

[7]李 铮.终端区扇区划设方法研究[D].天津：中国民航大学，2009.

[8]戴福青，洪兰收.空域交通复杂度计算方法研究[J].中国民航大学学报，2010，28（3）：1-4.

[9]何 毅.空中交通复杂度参数模型研究[D].上海：同济大学，2007.