覆冰导线机械式冲击除冰模拟研究

陈科全，严 波，刘小会，程皓月

（重庆大学 资源及环境科学学院工程力学系，重庆 400030）

覆冰常引起输电线路倒塔、断线、闪络和舞动等重大事故，严重威胁电力系统的安全运行。我国是输电线路覆冰最严重的国家之一，仅2008年年初冰雪灾害的直接经济损失就超过1100亿元。因此，输电线路除冰技术的研究具有极其重要的现实意义。

除冰技术的研究长期以来一直受到国内外业界的广泛重视。通常将用机械工具、自动化机器人和冲击波等方式进行除冰的方法称为机械除冰。机械式除冰的能耗通常比热力融冰法小100倍以上，因此倍受人们的关注。机械除冰方法最早有“ad hoc”法、滑轮铲刮法、电磁力除冰和电脉冲除冰等，这些方法各有特点，但是其安全性和除冰效率有待提高［1］。近年，电动机械装置［2］和机器人除冰［3］也得到了发展，由于这些装置夹持电缆、防滑和越障等能力的设计控制十分复杂，目前多处于理论实验阶段或仅针对特定线路有所应用。Leblond等［4］提出了一种地线除冰装置（DAC），该装置通过爆炸产生的冲击载荷进行除冰。Kálmán等［5］采用有限元软件ADINA模拟了脉冲载荷作用下单档地线的除冰过程，并假设覆冰的等效塑性应变达到极限值时即发生破坏，但覆冰等效塑性应变极限的取值缺乏依据。国内陈继东等［6］模拟了单档覆冰地线除冰以及冲击波在档内的传播过程，该文中覆冰采用了各向同性弹塑性J2本构模型，未对各种参数条件下的情况进行讨论。最近，本文作者采用有限元方法模拟研究了覆冰单导线和四分裂导线的除冰过程［7-8］，其中将覆冰简化为各向同性弹性体，重点研究了单档除冰的情况。

如何选择合理的覆冰本构模型是研究这一问题的关键。输电线覆冰属于多孔介质，其力学行为受晶体结构、温度和孔隙率等多种因素的影响。Cole［9］利用实验测得冰在不同应变率下的应力-应变曲线，发现高应变率时冰几乎为完全脆性，即可以忽略其塑性变形。Eskandarian［10］研究了输电线覆冰的多孔弹塑性本构模型，其指出在高应变率下覆冰可视为多孔弹性介质。

机械式冲击除冰过程中，覆冰的应变率较高，故可视其为多孔弹性介质。本文利用多孔弹性模型描述覆冰，并考虑温度和孔隙率的影响。在ABAQUS中利用用户材料子程序VUMAT实现覆冰本构模型的描述和覆冰失效判断，系统地模拟研究覆冰导线在冲击载荷作用下的除冰过程和除冰效果，为机械式除冰装置的设计提供参考。

1 输电线覆冰的力学性质

本文以硬雾凇为研究对象，假设其为均匀材料。根据文献［10］，硬雾凇可简化为横观各向同性体。与其它多晶体一样，可通过有效柔度（或刚度）张量建立输电线覆冰的多孔弹性模型，其有效柔度（或刚度）与无孔隙冰的有效柔度（或刚度）张量有关。根据广义虎克定律，硬雾凇的本构关系可表达为：

其中，εij为有效应变；σkl为有效应力；为有效柔度张量，它与孔隙率φ和无孔隙冰的有效柔度张量有关。

由于高应变率时孔隙率的变化很小，在此忽略孔隙率φ在变形过程中的变化，则硬雾凇的有效柔度张量可由下式计算：

覆冰破坏准则目前所见仅两种，一是文献［5］提出，并为文献［6］采用的等效塑性应变破坏准则，对于这一准则，文献［6］并未给出塑性破坏应变取值合理性的解释。另一个是文献［11］中提出的拉伸破坏准则，该准则已被文献［7-8］采用。文献［12］指出，输电线覆冰属于多孔材料，其拉伸强度几乎不随应变率和温度变化。对于多孔模型需确定不同孔隙率覆冰的拉伸强度。Zheng等［13］通过理论推导与实验相结合的方法，得到多孔材料拉伸强度σc与孔隙率φ满足：

式中：σc0为相应无孔隙材料的拉伸强度。根据文献［5］，无孔隙覆冰的拉伸强度σc0为2 MPa，由式（3）可求得不同孔隙率下覆冰的拉伸强度。

无孔隙冰的弹性常数按下式确定［10］：

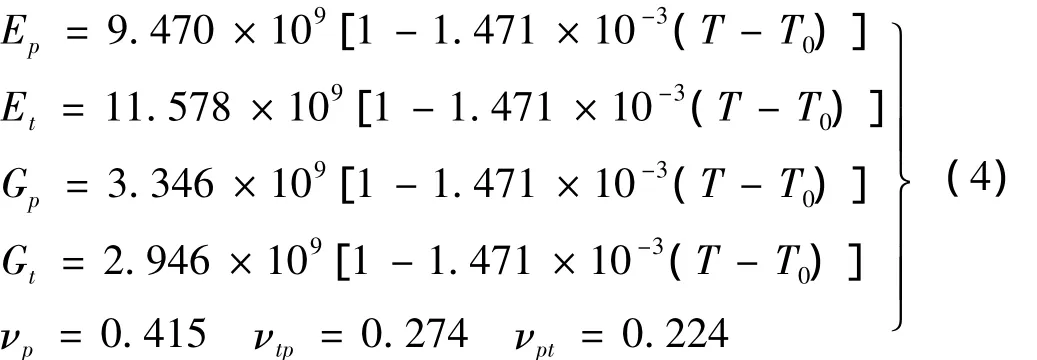
其中，下标t和p分别表示横向和各向同性面，T0为绝对零度（K），T为冰的当前温度（K）。本文讨论的机械式除冰方法在环境温度升高冰融化前即实施，因此，可以认为冰的温度和环境温度相同。

2 除冰过程有限元模拟

2.1 有限元模型

忽略杆塔变形，建立包含绝缘子串的多档覆冰导线模型，悬垂绝缘子串上端点约束线位移，可以自由转动；耐张绝缘子串的端部则完全固定。以三档耐张段为例，其简化模型如图1所示。

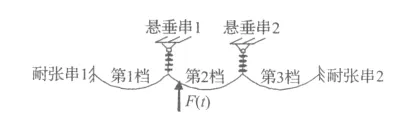
图1 三档耐张段机械除冰简化模型Fig 1 De-icing model for three-span line section

导线型号为A3/S3A-732/92，其相关物理力学参数如表1所示。导线的阻尼采用Rayleigh阻尼模型，即阻尼矩阵C是质量矩阵M和刚度矩阵K的线性组合：

其中：α和β分别为与结构和材料有关的常数。根据文献［14］，对于覆冰导线α可近似取0.14，β取0。悬垂绝缘子串长 6.47 m，总质量 460.8 kg，在此用半径0.05 m的圆截面梁简化。

由于输电线实际覆冰过程一般较缓慢，可忽略冰中的初始应力。假设覆冰均匀地附着在导线表面，如图2（a）所示。建立覆冰导线模型时，利用文献［15］提出的数值方法确定导线自重下的初始构形，该方法无需迭代计算。导线适宜用索单元模拟，在ABAQUS软件中，将桁架单元（T3D2）的材料性质设置为不可压缩即可实现索单元的模拟。覆冰用与导线相互平行且共节点的管梁单元（B31）模拟，如图2（b）所示。每个悬垂绝缘子串用1个空间梁单元模拟。

图1中所示F（t）为模拟机械除冰所施加的冲击载荷，加载时间和卸载时间分别为0.1 s和0.001 s。数值模拟时，首先计算导线在自重和覆冰载荷作用下的静力平衡状态，再施加冲击载荷模拟除冰过程。

表1 导线A3/S3A－732/92的物理力学参数Tab.1 Physical and mechanical parameters of conductor A3/S3A－732/92

图2 覆冰附着模拟Fig.2 Finite element modeling of conductor accreted with ice

2.2 覆冰破坏的模拟

为定义覆冰的多孔弹性本构关系，并删除覆冰破坏单元，用FORTRAN语言编写了用户材料子程序VUMAT。在模拟机械除冰过程中，子程序VUMAT不断计算和更新覆冰单元的应力，并由最大拉应力强度准则判断覆冰单元的破坏，当单元应力大于等于拉伸应力极限时即将该单元删除。VUMAT子程序的具体流程如下：

（1）从ABAQUS主程序中读入上一增量步结束时的应力张量σold、状态变量StateOld（nblock，nstatev）和本增量步的应变增量dε。

（2）计算相应无孔隙冰的弹性柔度矩阵和刚度矩阵。

（3）根据式（2）求硬雾凇的有效柔度张量，并求逆得其有效刚度矩阵。

（4）更新覆冰单元积分点的应力。

（5）覆冰单元失效判定及删除破坏单元。当覆冰单元的拉应力σll大于拉伸强度时，更新状态变量state-New（nblock，nstatev）=0，即删除该覆冰单元。反之，stateNew（nblock，nstatev）=1，即保留该覆冰单元。

（6）更新内能和非弹性耗散能。

（7）分析步时间（STEPTIME）和总时间（TOTALTIME）判定，时间结束即结束主程序，否则进入下一个时间步迭代。

3 计算结果及分析

3.1 孤立档除冰

以档距200 m，导线安装应力为34.33 MPa的孤立档为研究对象。覆冰厚度取10 mm、距离导线左端6 m处施加不同幅值的冲击载荷，研究覆冰采用横观各向同性多孔弹性模型和各向同性弹性模型时除冰率的差异，并进一步讨论除冰时的温度和冰的孔隙率对除冰效果的影响。覆冰多孔弹性模型中孔隙率取φ=0.13，环境温度T=263.16 K，代入式（4）、（2）即可确定冰的本构方程。此外，数值计算表明，当模拟导线的索单元和模拟冰的管梁单元长度取0.2 m时，能保证计算结果单元收敛性。

图3所示为在冲击载荷作用下，采用不同覆冰本构模型计算得到的除冰率随冲击载荷大小的变化。从图中曲线可见，覆冰为多孔弹性体时的除冰率远大于弹性体时的值，由定性分析这是合理的。如冲击载荷幅值为6 kN时，采用多孔弹性模型时导线上覆冰完全脱落，而采用弹性体模型时除冰率仅为45.4%，两者差异明显。

现在考察除冰时的温度对除冰率的影响。保持孔隙率φ=0.13，模拟三种不同温度下的除冰过程，结果如图4所示。可见，在计算的温度范围内，温度对除冰率的影响非常小。

图5所示为不同孔隙率下除冰效果的对比。可见，在相同条件下，除冰率随孔隙率的增大而增加，这是由于覆冰拉伸强度σc随孔隙率φ的增加迅速减小，即相同载荷作用下覆冰更易破坏而脱落。

3.2 连续档除冰

前面讨论了覆冰的本构模型、孔隙率和温度对孤立档除冰过程的影响，下面采用横观各向同性多孔弹性覆冰模型，在孔隙率φ=0.13和温度T=263.16K的条件下，模拟研究连续档覆冰导线受冲击载荷作用下的除冰过程。

3.2.1 三档连续档典型除冰过程数值模拟

现以档距200 m的三档连续档为例，参见图1。假设覆冰厚度10 mm，在距离第二档左端6 m处施加8 kN冲击载荷，数值模拟冲击载荷下的除冰过程。图6所示为数值模拟得到的除冰过程示意图。可见，加载过程中载荷作用点附近的覆冰已开始脱落，见图6（b）。覆冰在开始一段时间内从左向右依次脱落，这是由于此时弯曲应力占主导地位，导致覆冰的轴向应力超过强度极限而发生破坏。同时，由于悬垂绝缘子串1向右偏摆，第1档导线左端覆冰的轴向拉伸应力超过拉伸强度而脱离导线，见图6（d）。同理，绝缘子串2向左偏摆导致第3档右端部分覆冰脱落，见图6（e）。

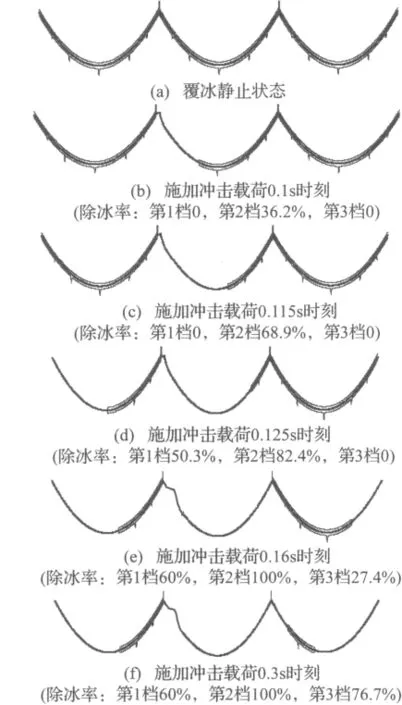
图6 冲击载荷作用下除冰过程模拟图Fig.6 De-icing process of iced conductor under shock-load

图7所示为8 kN冲击载荷作用下两个悬垂绝缘子串水平偏摆的时程曲线。冲击载荷作用下导线中将产生横波和纵波［7］，在连续档的悬垂绝缘子串处，波的一部分将反射，另一部分将传播到相邻档。波沿线路方向反复传播和相互作用，并逐渐衰减直至最终消失，这是一个非常复杂的过程。此外，从图7可见，由于悬垂绝缘子串2离载荷施加点较远，其运动响应滞后于悬垂绝缘子串1。该两悬垂绝缘子串偏摆的最大值出现在大部分冰脱落之后，这与脱冰后导线张力的变化有关。

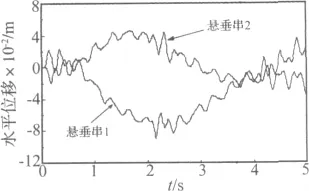
图7 冲击载荷作用下悬垂绝缘子串水平偏摆位移曲线Fig.7 Horizontal displacements of suspension insulator strings under shock-load

3.2.2 不同档数情况下除冰效果对比

现模拟分析档距200 m，档数分别为1，3，5三种情况下的除冰效果。假设覆冰厚度10 mm，距离中间档左端6 m处施加冲击加载。不同冲击载荷大小作用下不同档数线路除冰率结果如表2中所列。可见，冲击载荷作用档的除冰率最大；相同除冰载荷作用下档数越少除冰效果越好，说明邻档导线和悬垂绝缘子串对除冰效果的影响较大。下面以三档耐张段覆冰导线为研究对象，模拟研究冲击载荷大小、档距和覆冰厚度等对除冰效果的影响。

表2 不同档数下除冰效果的对比Tab.2 Rate of de-icing in the cases of different number of spans

3.2.3 除冰载荷幅值的影响

针对三档耐张段，假设档距为200 m，覆冰厚度为10 mm，距离第二档左端6 m处施加大小不同的除冰冲击载荷，模拟研究载荷幅值对除冰效果的影响。载荷的加载和卸载时间仍然分别为0.1 s和0.001 s。

图8所示为各档除冰率随冲击载荷载幅值的变化曲线。可见，加载档的除冰效率最大，且随冲击载荷幅值的增加而增大。加载档的覆冰在冲击载荷幅值为7kN时全部脱落，而相邻档的除冰率相对较小。

图8 冲击载荷幅值对除冰效果的影响Fig.8 Rate of de-icing varies with amplitude of shock load

3.2.4 档距的影响

针对前述三档耐张段模型，保持载荷幅值为6 kN，模拟研究不同档距下的除冰效果。表3所列为不同档距下各档的除冰率。可以发现，各档除冰率随档距的增加而减小，而且档距对加载档的除冰效果影响最大。因此，为达到较好的除冰效果，大档距覆冰输电线需施加更大的冲击载荷。

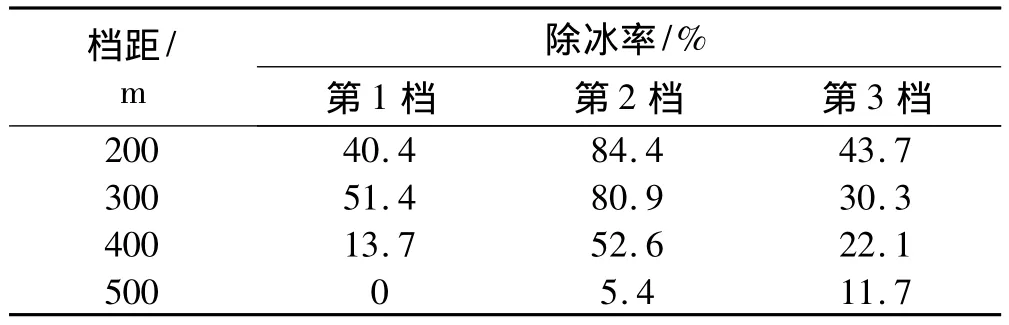
表3 不同档距下覆冰导线各档的除冰率Tab.3 Rate of de-icing in different span length

3.2.5 覆冰厚度的影响

最后，针对三档耐张段，保持档距200 m和载荷大小6 kN不变，模拟5 mm、10 mm、15 mm和20 mm四种不同覆冰厚度情况下的除冰效果。模拟得到的各档的除冰率如表4所列。可见，覆冰厚度越小除冰率越大，且加载档的除冰效果同样好于其它相邻档。因此，为达到较好的除冰效果，实际除冰时应在较大覆冰厚度形成前及时除冰。

表4 不同覆冰厚度下的除冰率比较Tab.4 Rate of de-icing in different ice thickness

4 结论

本文采用横观各向同性多孔弹性覆冰模型，利用ABAQUS软件数值模拟研究覆冰导线的机械除冰过程，得到如下结论：

（1）采用与实际更接近的横观各向同性多孔弹性覆冰模型，在相同除冰条件下得到的除冰率要高于将覆冰简化为各向同性弹性模型时的除冰率。

（2）除冰时的温度对除冰效果的影响较小，但除冰率随覆冰孔隙率的增大而增加。

（3）对于连续档覆冰导线，邻档导线和绝缘子串偏摆对除冰效果的影响较大，相同条件下，多档耐张段需要施加更大的冲击载荷才能达到较好的除冰效果。

（4）除冰冲击载荷越大，除冰效果越好，但实际实施时需考虑导线及杆塔等的承载能力。

（5）档距对除冰效果的影响明显，档距较大时需要施加更大的冲击载荷进行除冰。

（6）导线上覆冰厚度越小越容易除冰，为达到好的除冰效果，应在覆冰厚度较小时及时除冰。

值得一提的是，本文的目的是通过数值模拟对机械式冲击除冰方法的可行性进行研究，为下一步的深入研究确定方向。尚需开展模拟试验以验证方法的正确性和可行性。

［1］刘和云.架空导线覆冰防冰的理论与应用（第二版）［M］.北京：中国铁道出版社，2001.

［2］Montambault S，Cote J S，Louis M.Preliminary results on the development of a teleoperate compact trolley for live-line working［C］. Proceedings ofIEEE 9th International Conference on Transmission and Distribution Construction，2000：21-27.

［3］王 超，魏世民，廖启征.高压输电线上除冰机器人的系统设计［J］.机械工程与自动化，2010（1）：148-149.

［4］Leblond A，Lamarche B，Bouchard D，et al.Development of a portable de-icing device for overhead ground wires［C］.Canada：Proceedings of the 11th IWAIS，2005：399-404.

［5］ Kálmán T.Dynamic behavior of iced cables subjected to mechanic shocks ［D］. Quebec ：University of Quebec，2007.

［6］陈继东，张 予，刘晓虎.输电线路机械震动除冰装置仿真研究［J］.电瓷避雷器，2009（5）：5-8.

［7］陈科全，严 波，张宏雁.冲击载荷下导线覆冰脱落过程的数值模拟［J］.应用力学学报，2010，27（4）：761-766.

［8］严 波，陈科全，祖正华，等.覆冰四分裂导线除冰过程模拟研究［J］.振动与冲击，2011，30（11）：101-105.

［9］Cole D M.Strain-rate and grain-size effects in ice［J］.Journal of Glaciology，1987，33（155）：274-280.

［10］ Eskandarian M.Ice shedding from overhead electrical lines by mechanical breaking：a ductile model for viscoplastic behaviour of atmospheric ice［D］.Quebec：University of Quebec，2005.

［11］ Druez J，Louchez S，Bouchard G.Study of ice shedding phenomenon on cables［C］.Proceedingsofthe 9th International Conference of Offshore Mechanics and Arctic Engineering，1990：143-148.

［12］ Petrovic J J.Review.mechanical properties of ice and snow［J］.Journal of Materials Science，2003，38（1）：1-6.

［13］ Zheng M，Zheng X，Luo Z J.Fracture strength of brittle porous materials ［J］.International Journal of Fracture，1992，58（3）：51-55.

［14］Barbieri N，Honorate D S J O，Barbieri R.Dynamic analysis of transmission line cables，Part II-damping estimation［J］.Mechanical Systems and Signal Processing，2004，18（3）：671-681.

［15］ Yan B，Lin X S，Luo W，et al.Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load［J］.IEEE Transactions on Power Delivery，2010，25（1）：248-259.