巧借包络线方程 解斜抛中的极值问题

张文理

(南京师范大学附属中学 江苏 南京 210003)

研究斜抛运动的常见方法是运动的合成与分解，把运动看作是两个直线运动的叠加，根据不同的情景采用不同的分解方法，然后再进行数学处理．解斜抛中的极值问题，数据处理过程中会涉及到复杂的二次函数、三角函数极值运算，计算相当繁琐．选择合适的分解方法会在一定程度降低分析的难度，但无疑又对学生的思维和熟练程度提出了挑战．那么，是否存在普适的方法呢？我们不妨尝试借用包络线方程，去求解斜抛中的极值问题．

模型：一大炮发射炮弹，初速度为v0，忽略空气阻力和重力加速度变化的影响，求炮弹所能达到区域的边界方程．

分析：如图1所示，设定抛射点为坐标原点，在抛射平面(竖直平面)内建立直角坐标系xOy，沿水平方向和竖直向上方向分别建立x，y轴，θ为初始抛射角，此时，斜拋运动在水平方向上的分运动是匀速直线运动，t时刻的水平位移

x=v0tcosθ

(1)

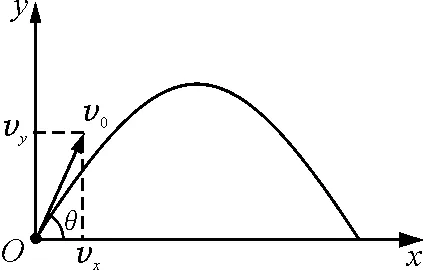
图1

在竖直方向上的分运动是竖直上拋运动，t时刻的竖直位移

(2)

(3)

改变θ，将形成一簇抛物线，此抛物线所能达到的区域边界曲线称为抛物线簇的包络线，抛物线与包络线相切，炮弹是不可能达到包络线以外的，如图2所示．

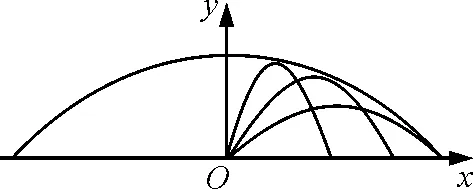
图2

将式(3)变形

(4)

式(4)即为包络线方程，是一条抛物线．对于三维空间，边界方程应为包络面方程，在此不作赘述．

研究包络线方程所包含的物理意义，可以得出这样的结论：在抛射速度v0确定的情况下，对于包络线上的某点(x，y)，若x值确定，y值必为斜抛过程中竖直方向所能达到的最大值；若y值确定，x值必为斜抛过程中水平方向所能达到的最大值；若对应于确定的某点(x，y)，v0则对应最小值．包络线方程所包含的物理意义为斜抛问题提供了思路和便捷．

1 “推掷铅球”中的极值问题

【例1】如图3所示,在掷铅球的运动中,如果运动员出手时的高度为h,速度大小为v0,问速度的方向与水平成多大角时掷得最远？最远射程为多少？

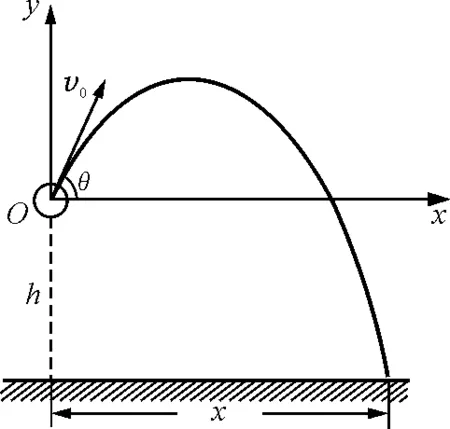
图3

解析：取抛出点为原点，建立如图3所示的直角坐标系，则落地点y=-h.

根据包络线方程

可得

解方程得

此值即为最远射程.

抛射角为

2 “翻越固定障碍物”中的斜抛问题

【例2】如图4所示，从A点以v0的初速度抛出一个小球，在离A点水平距离为s处有一堵高度为h的墙BC，要求小球能越过B点．问小球以怎样的角度抛出，才能使v0最小？

图4

解析：取抛出点为原点，包络线经过点(s，h)，根据包络线方程

可得

解方程得

此值为抛射速度的最小值.此时抛射角满足

3 “斜面”上的斜抛问题

【例3】如图5所示，在仰角α=30°的雪坡上举行跳台滑雪比赛，运动员从高处滑下，能在O点借助于器材以大小为v0的速度跳起，最后落在坡上A点，假如v0大小不变，问速度方向以与斜面方向成怎样的β角起跳能使OA最远？最远距离为多少？

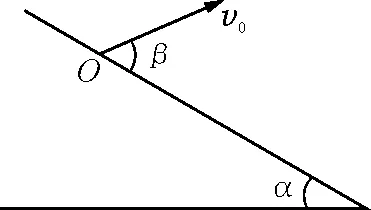
图5

解析：以抛出点为坐标原点，建立如图6(a)所示的直角坐标系，包络线方程为

斜面方程为

y=-xtanα

联立可得

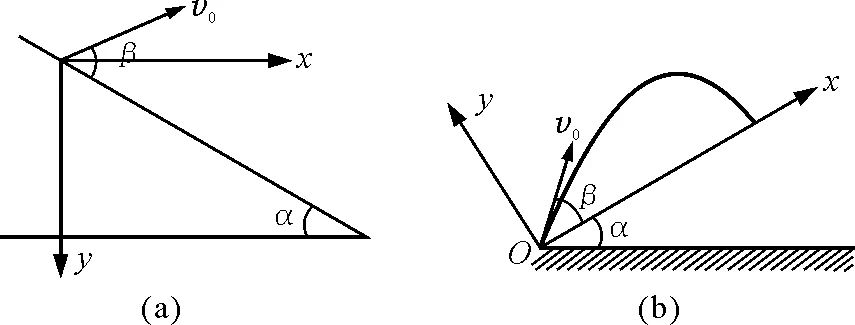
图6

此解即为水平方向的最大射程，LOA为沿斜面方向的最远距离，由几何关系易求得沿斜面的最远距离

此时抛射角θ(速度与水平方向的夹角)满足

如进一步运算，还可以得出：速度方向与斜面的

倾角满足

若改变抛射方式，从斜面底端抛射，如图6(b)所示，参照以上解题过程，我们很容易得出沿斜面的最远距离

速度方向与斜面的倾角满足

4 结语

通过以上分析，可以体会到包络线方程对解决斜抛中极值问题的广泛适用性和思路的便捷性.方法、模型的迁移推广，使学生极易掌握分析问题的一般方法，从而获得成功的体验．