P-内射的WB-环

李艳午，储茂权，程海霞，3

(1.芜湖信息技术职业学院，安徽芜湖 241000;2.安徽师范大学数学与计算机科学学院，安徽芜湖 241000; 3.南京大学数学系，江苏南京 210093)

0 引言

设R是环，M为右R-模，如果每个主右理想aR到M的右R-同态能够扩张成RR到M的同态，那么，称模M为右P-内射模;如果RR是右P-内射模，则称环R为右P-内射环［1］.内射性是关于环的一个很重要的性质，许多研究人员都对其做了深入而广泛的研究，取得了许多结果［1，2］.

环R称为正则环，是指对任意的a∈R，存在，b∈R，使得，a=aba.正则环的研究一直吸引着研究人员的兴趣，并取得了一些结果［3］.近年来，又有研究人员研究了正则环上的模比较结构，例如，陈焕垠［4］研究了正则的WB-环，得到了这种环上的部分比较结构.受此启发，本文研究了P-内射的WB-环，推广了文献［4］的部分结果，同时也使文献［1，2］的部分结果得到拓展和延伸.

1 预备知识

本文中的环R都是有单位元的结合环，称环R的理想I，J是正交的.如果，IJ=JI=0，设M和N为右R-模，M＜⊕N表示M同构于N的子模.设I是环R的理想，称a∈R是模I右(左)可逆，如果存在u∈R，使得，

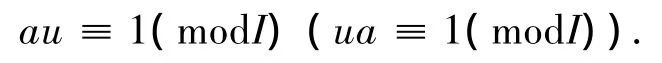
2 主要结果及证明

定理1 设R是非奇异的P-内射环，并且满足特殊左零化子的升链条件，则下列条件等价:

(1)R是WB-环;

(2)对任何a∈R，有正交理想I，J，使得，a=aua =ava，这里u∈R模I右可逆，v∈R模J左可逆.

证明 (1)⇒(2).

由于R是非奇异的P-内射环，所以存在一个环R的理想L，且L≠0，使得，l(a)⊕L是R的本质左理想［5］.令b∈L，且b≠0.如果r1，r2∈R，且使得，r1ba=r2ba，那么，(r1b-r2b)a=0，r1b-r2b∈l(a)∩L，考虑到，l(a)∩L=0，由此可推出，r1b=r2b.于是，我们可以定义，f:Rba→R，rba|→rb.易见，f是左R-同态.又因为R是P-内射的，从而存在x∈R，使得，rb=f(rba)=rbax1，对所有r∈R.特别地，对r=1，可得到，b=bax1，等式两边右乘a，又得到，b(a-ax1a)=0，b∈l(a-ax1a).再由，0≠b∈L和l(a)∩L=0，可推出b∉l(a).因此有，l(a)⊂≠l(a1)，这里，a1=a-ax1a.

重复上面的步骤，我们可以假定:

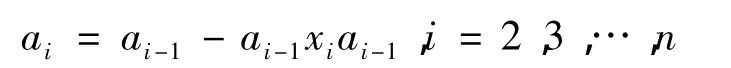
由于R满足特殊左零化子的升链条件，于是可以假定，l(an)=l(an+1).如果，l(an)=l(an+1)≠R，那么，an≠0.于是由上面的过程可推出，l(an)⊂≠l(an+1)，此与l(an)=l(an+1)矛盾.因此，我们得到，l(an)=l(an+1)=R，an=0，故，an-1= an-1xnan-1，an-1=an-2-an-2xn-1an-2.由文献［3］可知，an-1是正则的.类似地进行下去，最后得到，a= axa，对某个x∈R，即环R是正则环.于是对，a∈R，存在x∈R，使得，a=axa，x=xax，而ax+(1-ax) =1，故根据文献［4］有正交理想I，J和y，z∈R，使得，u=x+y(1-ax)∈R模I右可逆，v=x+z(1 -ax)∈R模J左可逆.容易验证，a=axa=aua= ava.

(2)⇒(1).

由于Goldie环是满足特殊左零化子升链条件的［6］，所以有:

推论1 设R是非奇异的P-内射环，如果R又是Goldie环，那么下列等价:

(1)R是WB-环;

(2)对任何a∈R，有正交理想I，J，使得，a= aua=ava，这里，u∈R模I右可逆，v∈R模J左可逆.

根据文献［7］的定理2，半素的P-内射环是非奇异的，所以结合定理1有:

推论2 设R是半素的P-内射环，如果R满足特殊左零化子的升链条件，那么下列等价:

(1)R是WB-环;

(2)对任何a∈R，有正交理想I，J，使得，a= aua=ava，这里，u∈R模I右可逆，v∈R模J左可逆.

定理2 设R是非奇异的P-内射环，如果R不包含由有限非零主左理想构成的直和项，那么下列等价:

(1)R是WB-环;

(2)对任何a∈R，有正交理想I，J和幂等元e∈R，使得，a=eu=ev，这里，u∈R模I右可逆，v∈R模J左可逆.

证明 (1)⇒(2).

令a∈R并且a≠0.由假设，存在x1∈R，x1≠0，使得，l(a)⊕Rx1⊆l(a1)，这里，a1=a-ax1a.如果，l(a1)=R，那么，a1=0，即，a=ax1a.若l(a1)≠R，则a1≠0.类似地，存在b2∈R，b2≠0，使得，l(a1)⊕Rb2⊆l(a2)，a2=a1-a1x2a1.由此，得到，l(a)⊕Rb1⊕Rb2⊆l(a2)，a1=a-ax1a，a2=a1-a1x2a1.

由于R不包含由有限个非零主左理想构成的直和项，那么重复上面的步骤，我们可以假定:

由l(an)=R，可推出an=0，因此，

最后，根据文献［5］，存在x∈R，使得，a=axa，即证明了环R是正则环.于是，对a∈R，存在x∈R，使得，a=axa和x=xax，又因为，ax+(1-ax)= 1，所以，u=a+(1-ax)y∈R模I右可逆，v=a+ (1-ax)z∈R模J左可逆.令e=ax，则e2=e∈R，且，a=eu=ev.

(2)⇒(1).

令a∈R，由于R是正则环，从而存在x∈R，使得，a=axa和x=xax.由假设，存在正交理想I，J和幂等元e=R，使得，x=eu=ev，这里，u∈R模I右可逆，v∈R模J左可逆.注意到，xa+(1-xa)=1，于是，eua+(1-xa)=1，从而，e+(1-xa)(1-e) =1-eua(1-e)∈R可逆，那么，x+(1-xa)(1-e)u=(1-eua(1-e))u，令u′=(1-eux(1-e))u，则，a=axa=au′a，这里，u′∈R模I右可逆.同理，存在v′∈R，使得，v′∈R模J左可逆.最后，由定理1得证R是WB-环.

称x，y∈R为相对于a是可交换的，如果axy= ayx，一个环R称为CF环，如果R的每个补左理想是有限生成的并且生成子的右单位元素相对于那个生成子是可交换的［4］，称，a，b∈R为相似.如果有可逆元u∈R，使得，a=ubu-1，记为a～b;称a，b∈R为伪相似.如果有x，y，≃z∈R，使得，xay=b，zbx= a，xyx=xzx=x，记为ab.下面就用伪相似来刻画P-内射WB-环.

定理3 设R是非奇异的P-内射环，如果R又是CF环，那么下列等价:

(1)R是W≃B-环;

(2)如果ab，a，b∈R，则有正交理想I，J，使得，au=ub，av=vb，其中，u∈R模I右可逆，v∈R模J左可逆;

(3)如果eR≅fR，e，f∈R为幂等元，则有正交理想I，J，使得，

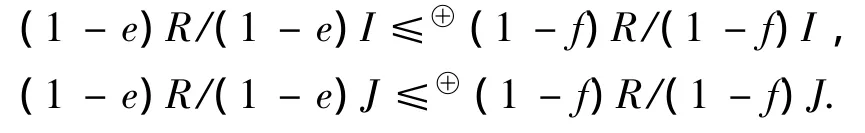
证明 根据文献［2］的定理5，由假设可知环R是正则的，再根据文献［4］的定理3.1得，(1)与(2)和(3)的等价性.

推论3 设R是非奇异的P-内射环，如果R又是CF环，那么下列等价:

(1)R是WB-环;

(2)如果aR≅bR，a，b∈R，则有正交理想I，J，使得，

证明 (1)⇒(2).

由条件以及文献［2］的定理5知，环R是正则环.如果，aR≅bR，a，b∈R，那么存在幂等元e，f∈R，使得，aR=eR，bR=fR，从而，eR≅fR.于是，由定理3知，存在正交理想I，J，使得，

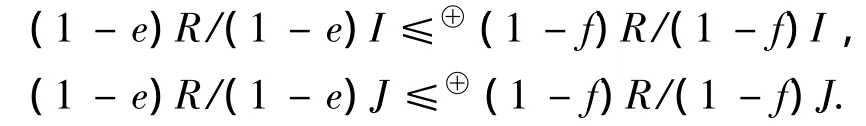
不难证明，

同理，

故，

(2)⇒(1).

假定eR≅fR，e，f∈R为幂等元，则有正交理想I，J，使得，

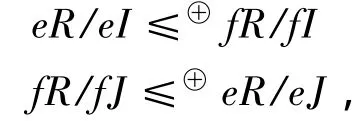
又易见，

同理，

最后，根据定理3知R是WB-环.

定理4 设R是非奇异的P-内射环，且满足特殊左零化子的升链条件，则下列条件等价:

(1)R是WB-环;

(2)如果aR≅bR，a，b∈R为幂等元，则有正交理想I，J，使得，au=ub，av=vb，这里，u∈R模I右可逆，v∈R模J左可逆.

证明 (1)⇒(2).

如果aR≅bR，a，b∈R为幂等元，则有，r1∈≃aRb，r2∈bRa，使得，a=r1r2，b=r2r1，由此可得，a

b.故由定理3得证.

(2)⇒(1)，是定理3的直接结果.

称a∈R有Drazin逆，如果存在，n∈N，r∈R，使得，an=an+1x，ax=xa，xax=x，称x为a的Drazin逆，记为ad.

定理5 设R是非奇异的P-内射环，则R只要再满足下列条件之一:

(a)特殊左零化子的升链条件;

(b)R是CF环;

(c)R是Goldie环;

(d)R不包含由有限非零主左理想构成的直和项.

就有，

(1)R是WB-环;

(2)如果ab，ba，a，b∈R有Drazin逆，则有正交理想I，J，使得，

这里，u∈R模I右可逆，v∈R模J左可逆，等价.

证明 (1)⇒(2).

首先，易知R只要再满足上述条件之一，那么R就是正则环.如果ab，ba，a，b∈R有Drazin逆，则存在，n∈N，使得，

从而就有，

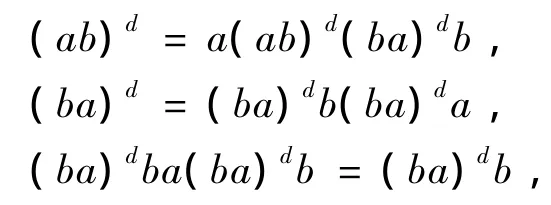
于是，

最后，由定理3可证.

(2)⇒(1).

如果aR≅bR，a，b∈R为幂等元，则有，r1∈aRb，r2∈bRa，使得，a=r1r2，b=r2r1.显然，a，b都有Drazin逆，于是有正交理想I，J，使得，

其中，u∈R模I右可逆，v∈R模J左可逆.由定理4得R是WB-环.

［1］Nicholson W K.Principally Injective Rings［J］.Journal of Algebra，1995，174(1):77－93.

［2］Zhang J L.P-injective Rings and Von-Neumann Regular Rings［J］.Northeast Math J，1991，7(3):326－331.

［3］Goodearl K R.Von Neumann Regular Rings［M］.London: Pitman，1979.

［4］陈焕垠.正则的WB－环［J］.数学学报，2006，49(6): 1311－1320.

［5］Faith C，Algebra II:Rings Theory［M］.New York:Springer-Verlag，1976.

［6］Chattes A W，Hajarnavis C R.Rings with Chain Conditions［M］.London:Pitman，1980.

［7］Zhang J L.On Nonsingular Rings［J］.Journal of Anhui Normal University(Natural Science)，1986，9(4):6－11.