保E增序完全变换的变量半群上的格林*关系

贾明斌，赵大亮

(1.山东职业学院基础部，山东济南 250104;2.山东师范大学数学科学学院，山东济南 250014)

1 预备知识

X表示全序集，设TX为X上的完全变换半群，f∈TX，若对任意的x∈X，都有f(x)≥x，则称，f为增序完全变换.X上的所有的增序完全变换关于完全变换的复合做成一个半群，记为T+(X).设E为X上的等价关系，f∈TX，若(x，y∈X)(x，y)⇒(f(x)，f(y))∈E，则称，f为保E的完全变换.X上的所有保E的完全变换构成 TX的一个子半群，记为TE(X).令，

则，T+E(X)为TE(X)的子半群.

设θ∈T+E(X)，在集合T+E(X)上定义运算如下，

此外，fθg为通常完全变换的复合，则在此新定义的运算下得到一个新的半群，称其为保E增序完全变换的变量半群，将其记为，T+E(X;θ).类似定义，TE(X;θ)，FE(X;θ).显然，TE(X;θ)和FE(X;θ)都为T+E(X;θ)的扩半群.在本研究中，我们将讨论T+E(X;θ)上的格林*关系的刻画.

用π(f)表示由X上的完全变换f所诱导的X上的一种分化，即，

定义，f*:π(f)→f(X)如下，f*(F)=f(F)，F∈π(f).显然，f*为双射.对X上的任子集A⊆X，记，

设f∈T+(X)，则有，f∈T+E(X)，当且仅当对任意B∈X/E存在B′∈X/E，使得，f(B)⊆B′.因此，若f∈T+E(X)，则对任意的A∈X/E，f-1(A)要么为一些E-类的并，要么为空集.对任意f∈T+E(X)记，

显然，E(f)也是X的一种分化，由π(f)，E(f)的定义知，对任意的M∈π(f)都包含在某个U∈E(f)中，即π(f)细化E(f).

设E为X上的等价关系，Y，Z为X的子集，f:Y→Z为一映射.若对(x，y)∈E，都有，(f(x)，f(y))∈E，则f称为保E的.若，(x，y)∈E，当且仅当(f(x)，f(y))∈E，则f称为保E*的.显然，f为保E的未必是保E*的.

2 T+E(X;θ)上的格林*关系

定理1 设f，g∈T+E(X;θ)，f≠g，则以下结论等价:

(iii)存在一个保E*双射，＞:f(X)→g(X)，使g=＞f，而且θ|f(x)和θ|g(x)为保E*的单射.

证明 (i)⇒(ii).

设(f，g)∈L*，则在T+E(X;θ)的扩半群中存在h，k，使f=k◦g=kθg，g=h◦f=hθf.由此及f，g∈T+E(X;θ)知，h，k∈TE(X;θ).由f=kθg知，π(g)细化π(f)，由g=hθf知，π(f)细化π(g).所以，π(f)=π(g).

又，f=(kθ)(hθ)f，所以，θ|f(x)是单射，进而有，π(θf)=π(f).类似地，θ|g(x)是单射，所以，π(θg)=π(g).从而有，

下面证明，

取U∈E(f)，则存在A，B，C∈X/E，使，

从而有，

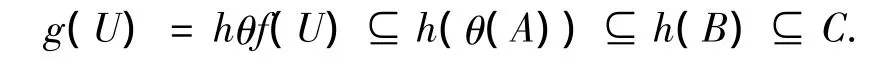
所以，

从而可得，E(f)细化E(g).类似地，E(g)细化E(f)，故，E(f)=E(g).

显然，E(f)细化E(θf).下设，V∈E(θf)，则存在A′，B′∈X/E，使

所以有，

进而有，

所以，E(θf)细化E(f)，从而有，E(θf)=E(f).类似地，E(θg)=E(g).从而有，

因为，π(θf)=π(f)，π(g)=π(θg)，所以，θ|f(x)和θ|g(x)都为单射，又，E(θf)=E(f)，E(g) =E(θg)，所以，θ|f(x)和θ|g(x)都为保E*的.

定义，

显然，＞为良定义的，而且，g=＞f.设x，y∈f(X)，则f-1(x)，f-1(y)为π(f)=π(g)中的不同元素，从而有，

故，＞ 为单射.又对 ∀y∈ g(X)设，x= f(g-1(y))，则，

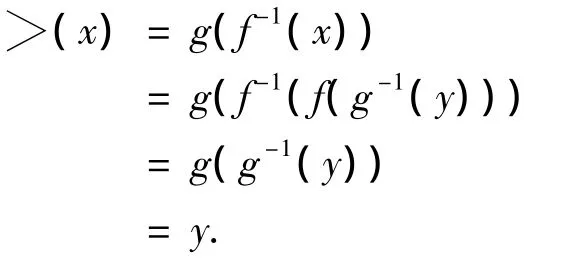
从而＞为满射，所以＞为双射.

下面证明＞为保E*的.

取，(x，y)∈E，x，y∈f(X)，则有，

f-1(y)包含在同一个U∈E(f)=E(g)内，⇔(＞(x)，＞(y)=(gf-1(x)，gf-1(y))∈E，即＞为保E*的.

假设条件(iii)成立，只需在T+E(X;θ)的扩半群TE(X;θ)中找到h，k，使得，

即可.

取A∈X/E，令A′=A∩θf(X)，以下根据A′可分两种情况进行讨论:

(1)若A′=＞，定义，h(x)=x，x∈A;

(2)若A′≠＞，设x，y∈A′，则存在x′，y′∈X，使得，

又，(x，y)=(θf(x′)，θf(y′))∈E，且θ|f(x)为保E*的，从而有，(f(x′)，f(y′))∈E.

设f(x′)∈B，存在B，C∈X/E，使＞(B)⊆C.取定c∈C，定义，

若存在x″∈X，使，x=θf(x″)=θf(x′)∈A′，又 θ|f(x)是单的，所以，f(x″)=f(x′)，从而有，＞(f(x″))=＞(f(x′))，故h在A上是良定义的.

类似地，可得h在X上是良定义的.

下面证明，h∈TE(X;θ).

设(x，y)∈E，则存在A∈X/E使得x，y∈A，令A′=A∩θf(x).同样，分两种情况进行讨论:

(1)A′=＞，则(h(x)，h(y))=(x，y)∈E.

(2)A′≠＞，则分以下几种情况讨论:①若x，y∈A′，则存在x′，y′∈X，使，(x，y)=(θf(x′)，θf(y′))∈E，又θ|f(x)为保E*的，从而有，(f(x′)，f(y′))∈E，又＞ 为保E的，从而有，(h(x)，h(y))= (＞(f(x′))，＞(f(y′)))∈E;②若x，y∈A-A′，则h(x)=h(y)=c，显然，(h(x)，h(y))∈E;③若x∈A-A′，y∈A′，则存在y′∈X，使y=θf(y′)，由h的定义知，(h(x)，h(y))=(c，＞(f(y′)))∈E，所以，h∈TE(X;θ).

下面证明，

取x∈X，令x′=θf(x)，则，

从而有，

类似地，存在k∈TE(X;θ)，使，f=kθg，所以，

定义1 设φ:π(f)→π(g)，若对任意的E类-A，都存在，B∈X/E，对每一个P∈πA(f)，都有θ(B)∩φ(P)≠＞，则φ称为容许Eθ的.另外，若φ为双射，而且φ，φ-1都是容许Eθ的，则φ称为容许E*的.θ

定理2 设f，g∈TE+(X;θ)，则以下结论等价:

(ii)对任意的E-类A，都存在B，C∈X/E，使，

(iii)存在一个容许 E*θ的双射，ψ:π(f)→π(g)，使，f*=g*ψ.

证明 (i)⇒(ii).

设(f，g)∈R*，则存在T+E(X;θ)的某个扩半群中元h，k，使，

由此及f和g为保E的知，h，k∈TE(X，θ).

对任意的E-类A，都存在，B，C∈X/E，使h(A)⊆B，k(A)⊆C，从而有，

由(ii)知，f(X)=g(X)，现定义，ψ:π(f)→π(g)，如下，

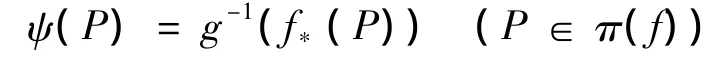
显然，ψ为良定义双射，而且，f*=g*ψ.

下面证明ψ为容许E*θ的.

设A∈X/E，存在B∈X/E，使f(A)⊆gθ(B).记，

则，xi∈f(A)⊆gθ(B)，而且存在，y∈θ(B)，使xi=g(y)，从而有，y∈θ(B)∩g-1(xi)，进而有，

所以，ψ为容许Eθ的.

类似地，ψ-1为容许Eθ的.

故，由定义可知，ψ:π(f)→π(g)，为容许E*θ的双射.

假设(iii)成立，以下在扩半群中找h，k，使，

对任意的E-类A，设B∈X/E，使得，

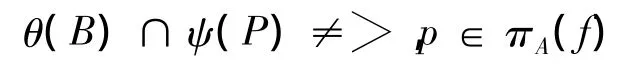
对任意x∈A，令Px=f-1(f(x))，取z∈θ(B)∩ψ(Px)，则存在，y∈B，使z=θ(y).

定义，h(x)=y，显然h存在.记，

则有，

从而有，类似地，存在k，使，g=fθk.从而有，(f，g)∈R*.

由以上两个定理可立即得出以下结论.

定理3 设f，g∈T+E(X;θ)，则以下结论等价:

(ii)π(θf)=π(f)=π(g)=π(θg)，E(θf)= E(f)=E(g)=E(θg)，同时对任意的E-类A，都存在，B，C∈X/E，使，f(A)⊆gθ(B)，g(A)⊆fθ(C).

定理4 设f，g∈T+E(X;θ)，则以下结论等价:

(ii)存在一个容许E*θ的映射，ψ:π(f)→π(g)和一个保E*双射，＞:f(X)→g(X)，且＞可表示为两个双射的乘积，使＞f*=g*ψ，而且，θ|f(X)和θ |g(X)都是保E*单射.

证明 (i)⇒(ii).

设(f，g)∈D*，则在T+E(X;θ)的扩半群中存在h，k，使，

则由定理2知，

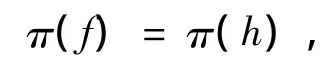
而且存在保E*双射，＞1:f(X)→h(X)，使得，h =＞1f，从而有，h*=＞1f*.而且由定理1知，θ|f(X)和θ|h(X)均为保E*单射.

类似地，存在保E*双射，＞2:k(X)→g(X)，使得，g=＞2k，从而有，g*=＞2f*.而且由定理1知，θ|k(X)和θ|g(X)均为保E*的单射.

又由定理2知，h(X)=k(X)，从而存在容许E*的双射ψ使，h=kψ.θ**

综上可得，

进而可得，

所以，＞ =＞2＞1.ψ即为所求，命题得证.

只需找到h，k，使，

由于＞可表示为两个双射的乘积，设这两个双射为＞1，＞2，＞ =＞2＞1.

(1)先定义h.令π(f)=π(h)，设，＞1:imf→imh，即h=＞1f，从而h被确定.

(2)再定义k.令π(k)=π(g)，设＞2:imk→img，即g=＞2k，从而k被确定.

下面只需证明k，h有R*关系即可.由前面有，

代换得，

又，h=＞1f，即得，h*=＞1f*.由g=＞2k得，g*=＞2k*.又，＞f*=g*ψ，变换得，h*=k*ψ，由定理2得，hR*k.

综上得，

从而有，

由预备知识知，αL*β时，kerα=kerβ，显然有，|imα|=|imβ|;由预备知识知，αR*β时，imα= imβ，显然有，|imα|=|imβ|.从而可得出以下引理，

引理1(α，β)∈T+E(X;θ)，若α∈J*(β)，则|imα|≤|imβ|.

进而可得以下推论，

推论1 在T+E(X;θ)中，有D*=J*.

［1］Howie J M.Fundementals of Semigroup Theory［M］.New York:Oxford University Press，1995.

［2］Hall T E.Congruence and Green＇s Relations on Regular Semigroups［J］.Glasgow Mathematical Journal，1972，13(2): 167-175.

［3］Pei Huisheng.Regularity and Green＇s Relation for Semigroups Transformations Preserving an Equivalence Relation［J］. Commmunications in Algebra，2005，33(1):109-118.

［4］Pei Huisheng，Zou Dingyu.Green＇s Equivalences on Semigroups of Transformations Preserving Order and an Equivalence Relation［J］.Semigroup Forum，2005，71(2):241-251.