一个新混沌系统的同步控制及其在保密通信中的应用

梅小华

(河西学院数学与统计学院，甘肃张掖 734000)

这里，控制输入选择为，

0 引言

自1990年，Grebogi等提出OGY混沌控制法，以及Pecora等提出完全同步以来［1］，研究人员对混沌系统的认识更加深入，混沌同步已经成为非线性科学理论及应用的重要组成部分及混沌研究的热点问题.到目前为止，学者们已经提出很多实现混沌同步的方法，例如，驱动响应同步法、线性反馈同步法、自适应控制同步法［2－5］等.本文研究了一类新混沌系统的同步问题，基于李雅普诺夫稳定性理论，利用激活控制法以及参数未知时自适应控制实现该系统的自同步，同时，本文利用归纳、推论和定理，以及仿真实验进一步证明了这些结论的正确性，最后，采用自适应混沌同步方法进行保密通信实验，实验结果表明，利用混沌掩盖可以有效地恢复出信息信号.本方法易于实现，收敛速度快，并且可以推广到其他类似系统.

1 一个新混沌系统的数学模型

在文献［6］中，马海军等通过对分岔混沌拓扑结构与全局复杂性的研究，建立了一个混沌系统，

当该系统取参数，a=0.9，b=0.2，c=1.2，初始条件为［2，1，2］时，利用Matlab可得到混沌系统(1)的三维相图如图1所示.

图1 混沌系统(1)的三维相图

2 参数不确定时混沌系统的同步

在实际中，许多动力系统具有参数或模型的不确定性，尤其随着环境的改变，系统的参数可能会发生变化.比如，在通信系统中，发送机和接收机的结构和参数完全相同的混沌同步通信是不现实的.因此，对参数未知的不确定的混沌系统的同步研究具有重要的实际意义，这个时候可以利用自适应同步方法实现混沌同步.设驱动系统为混沌系统(1)，则其响应系统为，

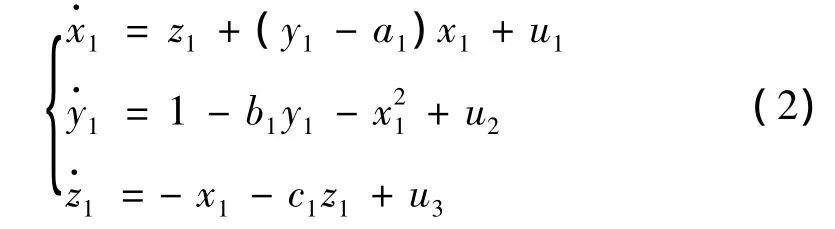
设状态误差和参数误差为，

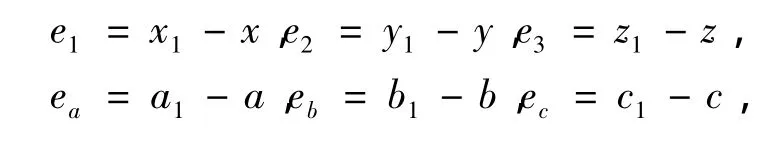
其中，a1，b1，c1是对a，b，c的估计，则系统误差为，

构造李雅普诺夫函数，

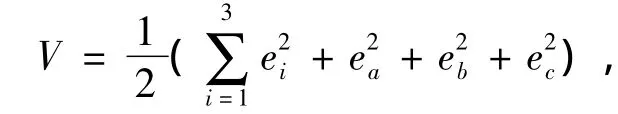
则，

选择如下控制器，

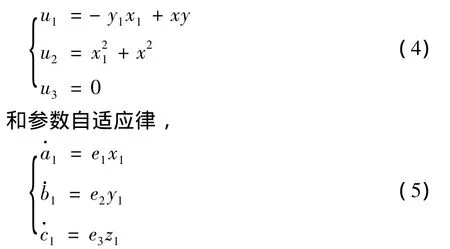
此时，

当参数a，b，c都大于等于零时，V·为负定，根据Barbalat引理，知，

即驱动和响应系统达到同步效果.因此，对任何的初始状态，选择自适应控制器(4)和自适应律(5)，可以使得响应系统和驱动系统达到同步，于是，得到如下定理.

定理1 对于驱动系统(1)和响应系统(2)，如果参数自适应律选择(5)，反馈控制器选择(4)，则驱动系统和响应系统将达到全局渐进同步.

3 基于激活控制的混沌同步

设驱动系统为混沌系统(1)，响应系统为，

设，

则系统误差为，

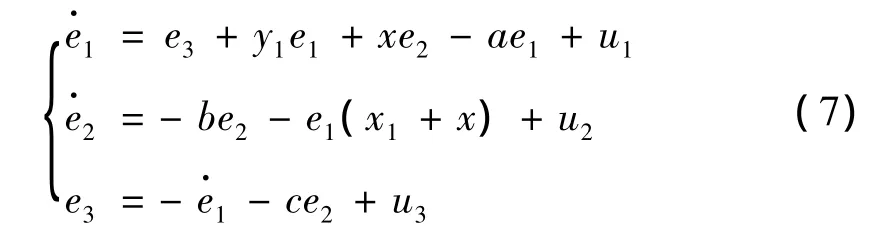
定义激活控制函数，U=(u1，u2，u3)T，为，

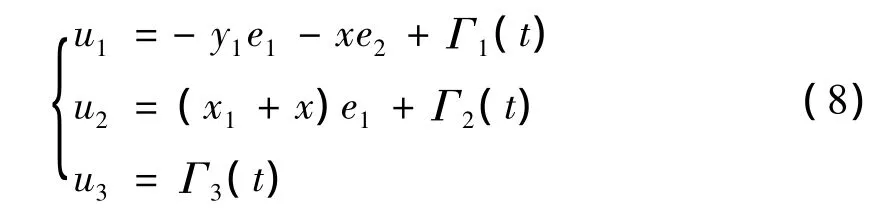
这里，控制输入选择为，

此时，闭环的特征根为:-1，-1，-1.于是，当t→∞时，‖e1‖→0，‖e2‖→0，‖e3‖→0，意味着驱动和响应系统可以实现混沌同步，于是，可得到如下的定理.

定理2 对于驱动系统(1)和响应系统(6)，如果系统的激活控制器取(8)，控制输入取(9)，则驱动系统(1)和响应系统(6)可以实现全局渐进同步.

4 数值模拟结果

为了验证我们所设计的混沌控制器的有效性，本文采用四阶龙格—库塔方法进行仿真.

例1 取驱动系统(1)的初值为(0.7，0.5，0.8)，响应系统(2)的初值为(0.6，0.3，0.5)，参数取，a=0.9，b=0.2，c=1.2.误差时序图的仿真结果如图2所示.

图2 自适应同步的同步误差

由图2可知，虽然驱动系统(1)和系统(2)的初值不同，但还是很快实现了该混沌系统的自同步.图3表示的是参数的估计随时间变化的曲线图，可以看出，随着时间的变化参数收敛到真值.

图3 参数的的估计

例2 取驱动系统(1)的初值为(-0.07，0.55，0.18)，响应系统(6)的初值为(0.46，0.43，0.75)，参数取，a=0.9，b=0.2，c=1.2.误差e1、e2、e3时序图的仿真结果如图4所示.

图4 激活控制同步的同步误差

由图4可知，虽然驱动系统和(1)响应系统(6)的初值不同，但仍然很快实现了该混沌系统的自同步.显然，这种方法具有很大的局限性.

5 利用自适应同步控制实现保密通信

近年来，混沌同步保密通信已成为科研人员研究的一大热点.混沌掩盖通信系统的工作原理如图5所示，其基本原理是:发送端的混沌系统输出类似噪声的混沌信号，在混沌信号上叠加需要掩盖的有用信号，将合成信号通过信道发送出去;在接收端与发送端混沌系统达到同步后，从接收端的混合信号中减去重构的混沌信号，从而解调出发送端的有用信息.在图5中，x(t)为发送系统的状态变量，m(t)为要传送的信息信号，s(t)为混沌掩盖后的传输信号，x′(t)为接收系统的状态变量，m′(t)为接收端恢复的信息信号.

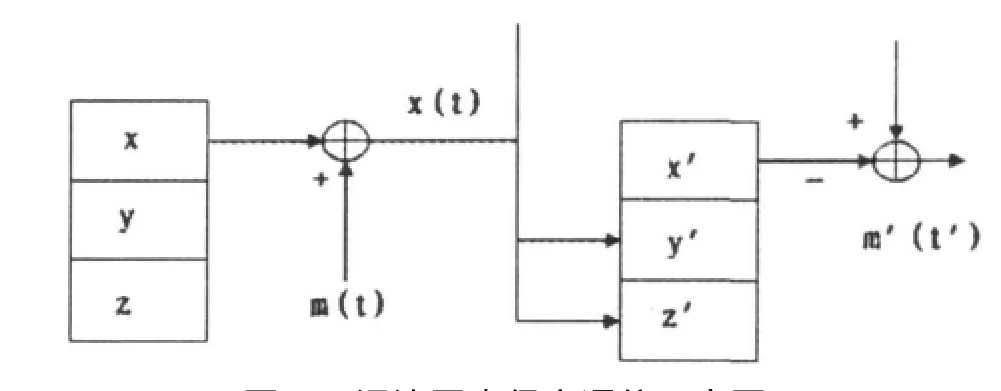
图5 混沌同步保密通信示意图

根据混沌掩盖保密通信原理，可将自适应同步的混沌系统应用于保密通信中.设需要传输的信息信号是m(t)=sint，则在发送端将有用信号与混沌信号x(t)相加，输出类噪声信号，s(t)=sint+ x(t)，驱动系统为(1)，响应系统为混沌系统(2).响应系统(2)通过控制器(4)可在接收端接收混沌信号x′(t)，只需从s(t)中减去受控系统中产生的混沌信号x′(t)，就可以获得还原的有用信号，m′(t) =s(t)-x′(t).原始信号与还原信号的信号误差为，e(t)=m(t)-m′(t).原始有用信号如图6所示，通过混沌保密系统后恢复出的信号如图7所示，传输过程如图8所示.显然，经过较短时间后，有用信号与解调出来的信号的误差几乎为0.另外，利用自适应控制方法响应系统的参数还可以是未知的，可见这种方法应用于保密通信的有效性.

6 结 语

本文研究了一类新混沌系统的同步问题，基于李雅普诺夫稳定性理论，利用参数未知时自适应控制方法构造非线性控制器以及激活控制实现该系统的自同步，仿真实验验证了方法的正确性.最后，采用自适应混沌同步方法进行保密通信实验，实验结果表明，利用混沌掩盖可以有效地恢复出信息信号.此外，在参数不确定的条件下，自适应同步法可同时完成混沌系统的参数辨识和同步，这种方法用于保密通信具有更高的保密效果.

［1］方锦清.非线性系统中混沌的控制与同步及其应用前景(二)［J］.物理学进展，1996，16(2):137－159.

［2］陈保颖.线性反馈实现Liu系统的混沌同步［J］.动力学与控制学报，2006，4(1):41－43.

［3］于洪洁.对称非线性耦合混沌系统的同步［J］.物理学报，2005，54(7):3029－3033.

［4］贾贞，邓光明.超混沌Lu系统的线性与非线性耦合同步［J］.物理学报，2007，5(3):220－22.

［5］黄纬.张化光，王智良.参数未知的不同结构系统的自适应同步［J］.系统仿真学报，2005，17(11):2689－2700.

［6］马海军，陈予恕.一类金融系统分岔混沌拓扑结构与全局复杂性研究(I)［J］.应用数学和力学，2001，22(2): 1119－1128.