影响我国台风频数与强度变化趋势预测

刘坦然，刘冬雪，薛东升，王炯炯

(1.中国海洋大学 数学科学学院，山东 青岛 266100;2.浙江省河海测绘院 水文分院，浙江 杭州310008;3.海洋石油工程股份有限公司工程项目管理中心，天津 300452;4.中国海洋大学网络与信息中心，山东青岛 266100)

影响我国台风频数与强度变化趋势预测

刘坦然1，刘冬雪2，薛东升3，王炯炯4

(1.中国海洋大学 数学科学学院，山东 青岛 266100;2.浙江省河海测绘院 水文分院，浙江 杭州310008;3.海洋石油工程股份有限公司工程项目管理中心，天津 300452;4.中国海洋大学网络与信息中心，山东青岛 266100)

首先使用滑动平均的方法，对近58年影响我国的台风频数、强度和年极值强度进行趋势分析，又使用Spearman非参数趋势检验法进行了显著性检验。在此基础上应用基于分形理论的R/S方法对未来的台风频数、强度和年极值强度进行了趋势预测。分析表明，未来影响我国的台风频数、强度、年极值强度都是呈增加趋势的;而且年台风频数和台风强度呈正相关性。

台风;滑动平均;Spearman趋势检验;R/S分析

我国是台风多发的国家，1949～2006年有近1300次台风对我国造成了不同程度的影响。尤其是南海和东海海域影响最大，且台风在强度达到最强时的位置有向北移动的趋势［1］。海洋工程的年极值波高和设计风速的推算一般有两种方法:1)年极值法，一般推算一个港区的设计风速年极值波高时，取该地区连续20年以上的数据，每年取最大值，用Gumbel，Weibull，P-III或者最大熵分布对其进行分析，画出经验累积频率分布图，从图上读出百年一遇或者五十年一遇的值;2)复合分布法［2-3］，设每年台风出现频次为n(0，1，…，k，…)，其相应概率为 P=(n=k)=Pk，(Pk=P0，P1，…，Pk)，若风速或者波高极值分布函数为G(x)，则二者复合极值分布可表示为

假设服从Poisson分布，用表示平均每年台风出现次数，则有

将式(2)代入式(1)得

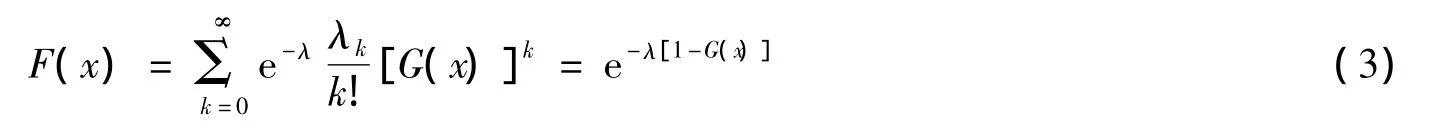
若G(X)分别符合Gumbel，Weibull，P-III或者最大熵分布，则可得不同的复合极值分布，复合极值分布充分考虑了台风的影响。

在一个台风多发地带，每年的风速最大值和波高最大值也都是由台风产生的。可以这样认为强度最小的台风对一个海区产生的最大风速最大波高也比没有台风时产生的最大值大。所以对于台风多发地带，准确地对台风发生的频数和强度进行预测显得非常有必要。

政府间气候变化委员会(Intergovernmental Panel on Climate Change，IPCC)第四次评估报告显示，近100年全球地表平均气温升高0.74℃。全球气温持续升高导致冰川融化，海水膨胀，水温升高，最终导致海平面上升。洋面气温升高，海水蒸发加快，可能会推动台风的形成，导致气候的不稳定。很多学者对气候变暖背景下台风发生的频率和趋势进行了研究。赵宗慈［4］通过统计和动力降尺度模型和模式分析较为一致地预计西北太平洋和北大西洋强台风强度和频数有可能增强。根据Emanuel(1987)提出的台风最大潜在强度理论(Maximum Potential Intensity，简称MPI)预测海平面气温升高1℃，热带气旋中心最大风速增强5%左右。MPI理论同时隐含增暖的海平面会导致热带气旋强度更强。Emanuel在2005年提出海平面气温增高台风总能量指数PDI(Power Dissipation Index)增加。Holland(1997)，Henderson-Seller等(1998)推断，海平面温度升高会导致台风的MPI增大，即台风强度可能更强或强台风增多。Emanuel等(2006)将大西洋的PDI序列延伸至1800年代后期，分析发现该序列与大西洋台风主要源地的海平面气温的长期变化(尤其是世纪尺度的变暖趋势)相当接近，并与局地的海平面温度存在很好的正相关性。Sriver等(2006)估算了全球台风PDI的敏感性，发现海平面每增加0.25℃，全球台风的PDI将增加约60%。由于20世纪70年代中期海平面发生了基本态的变化，即海平面温度升高0.5℃～1.0℃(1990年以后升高0.5℃)，这种升温被认为与全球气候变暖有关，因而近30年台风强度的增强可能与全球气候变暖有关［5］。分析上述研究成果，可以认为:随着气温的进一步升高，台风的强度可能会进一步加大。

但是，张颖［6］指出，全球变暖的背景下，环境场的变化可能有利于台风活动的发生，但是目前关于环境场对于台风活动的影响和相互关系还缺乏足够的认识，环境场的变化对于台风活动会有怎样的具体影响还有待于进一步深入分析。

随着全球气温的升高，对于台风的影响，还没有一个确切的认识，还存在很大的争议。而台风的发生对于台风多发地带海洋工程的设计又有着如此重要的影响。所以有必要进一步对台风的发生趋势进行研究。以期在海洋工程的设计中考虑到这些因素，实现海洋工程的安全使用。

1 分析方法

使用目前常用的气象水文变化趋势分析方法——Spearman秩次相关非参数趋势分析法和滑动平均的方法，对过去的变化趋势一致性进行分析和验证。然后使用R/S分析(Rescaled Range Analysis，重新标度极差分析)方法，根据1949～2006年影响我国台风的数据，对台风发生的频次和强度年极值强度进行了长期的趋势预测分析。

1.1 Spearman趋势检验

设样本(X，Y)={(X1，Y1)，…，(Xn，Yn)}取自 F(x，y)的独立样本。假设检验问题是:

H0:X与Y不相关↔H1:X与Y相关

对上面的假设，若H1成立，说明X与Y有相关性，即随着X的变化，Y有着相应的响应。如果用Ri表示Xi在X1，…，Xn中的秩，Qi表示Yi在Y1，…，Yn中的秩，则Ri与Qi具有同步性。用rs作为度量两个变量的相关性［7-8］。则得:

秩相关系数rs服从对称分布，其对称中心为原点o。查秩相关系数检验临界值表可查得cα的值。若rs≥cα，则认为X与Y正相关;若rs≤-cα，则认为X与Y负相关;否则认为X与Y相互独立。

1.2 R/S分析方法

R/S分析方法是H E Hurst于1965年提出的一种时间序列统计方法，在分形理论中有着重要的作用［9-10］。自从2002年王孝礼将其引入水文与水资源的研究中［9］以来，R/S分析方法在水利工程中的应用得到了极大的推广。分析表明R/S分析方法是适合水利方面的研究的［9-12］。R/S分析方法的基本原理:

考虑一个时间序列{ξ(t)}，t=1，2，…，对于任意正整数τ≥1，定义均值序列

用X(t)表示累积离差:

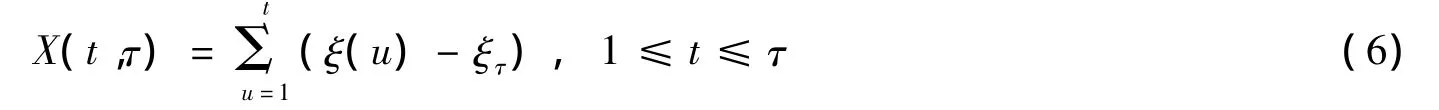
极差R定义:

标准差S定义:

赫斯特和费勒证明了如下结果:

式中:H表示赫斯特指数。

一维布朗样本函数的赫斯特指数H(0＜H＜1)与分形维数D0有关系:

分维D0表示运动轨迹的不平滑和运动的激烈程度，所以对于一维布朗运动函数，随着H的减小，D0增大，其运动轨迹的平滑程度越差，变化越激烈。1)H＜0.5，意味着未来的总体趋势将与过去相反，即过程具有反持续性(antipersistence)。H越接近0，反持续性越强，过去的增加趋势预示着未来的减少趋势，过去的减少趋势预示着未来的增加趋势。2)H=0.5，即各项指标完全独立，相互没有依赖，未来具有随机性。3)H＞0.5意味着未来的趋势与过去一致，即过程具有持续性(Persistence)，H越接近1，持续性就越强。

2 影响我国台风频数趋势分析

2.1 滑动平均法

1949～2006年共有近1 300次台风对我国沿海造成影响①台风的数据来自中国台风网http://www.typhoon.gov.cn/data/search.php?type=999(这里是说影响我国台风的次数，而不是台风发生的次数，比如说1990年第24号台风Dot，先于1990年9月3日早8点影响我国台湾省，之后往西北方向前进，再于9月7日晚8点影响我国诏安到惠安地区，最后又于9月10日晚8点影响我国阳江到海丰地区。虽然是一次台风，但是分三次对我国不同区域造成影响，故算作3次台风。中国台风网上给的资料也以199 024，199 024s，199 024s-1标示。研究的是影响我国的台风频数和强度变化趋势，而台风是在大洋深处外海形成的，但是有时一个台风可能分几次对我国领域造成影响，台风的影响次数比发生次数更有意义)，见图1和图2。图1对台风发生频数进行了五年滑动平均处理，并对五年滑动平均值进行了一次线性拟合。其中一次拟合函数:

图2对台风发生频数进行了十年滑动平均处理，并对十年滑动平均值进行了一次和二次拟合。其中一次拟合函数:

二次拟合函数:

从图1图2中可以看到，不管是对数据进行5年滑动平均还是10年滑动平均处理，对滑动平均值进行一次拟合还是二次拟合，从图上可以看到自1960年之后每年台风发生的频数都有一个下降的趋势。

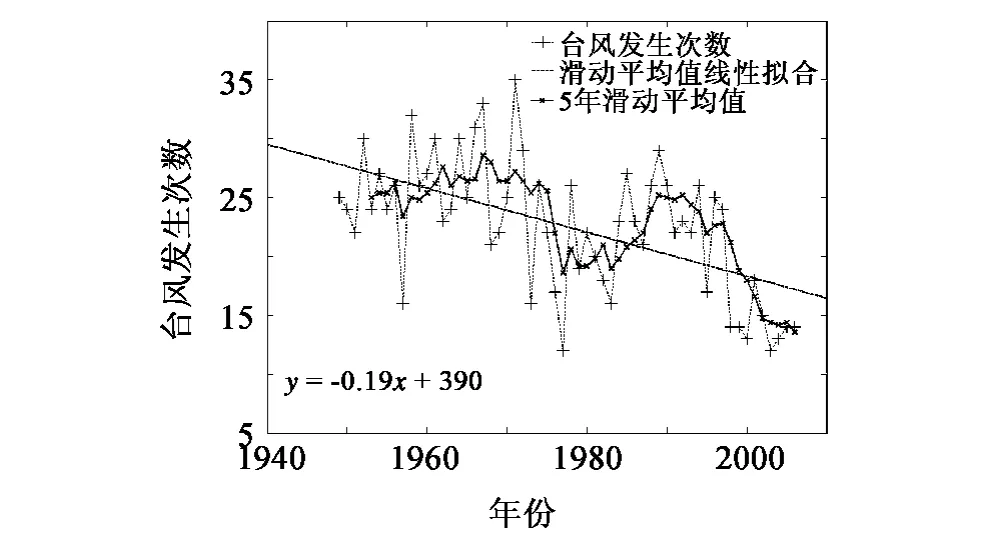
图1 影响我国台风频数及五年滑动平均Fig.1 Typhoon frequency and 5-year running average

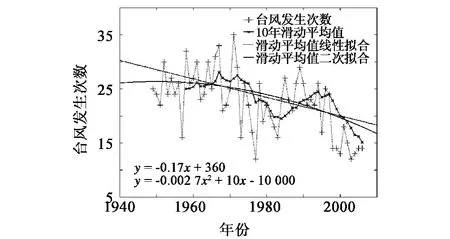
图2 影响我国台风频数及十年滑动平均Fig.2 Typhoon frequency and 10-year running average

2.2 Spearman 趋势检验

先计算出年份对应的秩和年台风频数对应的秩，见图3。

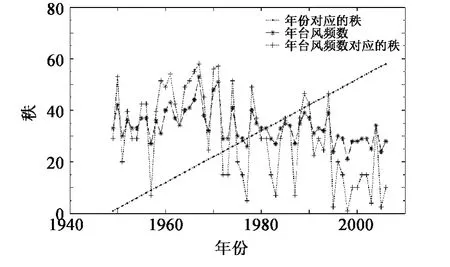
图3 年份和年台风频数对应的秩Fig.3 In year and annual typhoon frequency＇s rank

算得rs=-0.53。查秩相关系数检验临界值表得P(rs≤ -0.306)=0.01，说明 P(rs≤ -0.53)＜0.01，由于0.01很小，所以拒绝原假设，认为年台风频数和时间成负相关性。即在过去的半个世纪里随着年份的增加台风频数呈显著下降趋势。这和图1、图2上看到的结果是一致的。

2.3 R/S分析法预测

把台风发生频数从小到大进行排列，以累计频率25%的点作为分割点，频次小于等于分割点的算作台风发生少的年份。即台风发生频数不高于17次的年份看成台风发生少的年份。把1948年作为计算零点，可得表1。

表1 影响我国年台风频数的R/S分析Tab.1 Annual typhoon frequency's R/S analysis

经过计算，得到H=0.249 8。在对数坐标中画出(ln(i)，R(i)/S(i))，并用线性拟合，结果见图4。H＜0.5，说明未来是反持续性的，将来的趋势与过去相反，也就是说未来影响我国台风的频数在R/S分析下是呈现增加的趋势。这与文献［6］、［13］以及 Holland(1997)，Henderson-Seller(1998)和 Emanuel(2006)等［5］的研究结果是一致的，即随着气温的升高台风的频数会增加，当然这是从统计的角度得出的结论。

3 影响我国台风的强度分析

选取台风发生时产生的最大风速作为台风强度的指标，有理由认为台风产生的中心最大风速大则台风强度就大。

由于这里讨论的是台风强度的发展趋势，所以在以年为单位的时间内，强度最大和最小台风的产生可能有一些偶然因素，它们可以看作台风强度总趋势外的偶然因子。所以在研究年台风强度发展趋势时，参考评委打分系统，去除每年强度最大和最小的台风，剩下的取平均值作为该年台风强度的评判因子。则可得每年的台风风速，见图5及图6。其中图5对年风速进行了5年滑动平均处理，图6对年风速进行了10年滑动平均。可以明显的看到近50年来台风的强度呈明显的下降趋势。

图4 影响我国年台风频数的R/S分析结果Fig.4 Annual typhoon frequency＇s R/S analysis

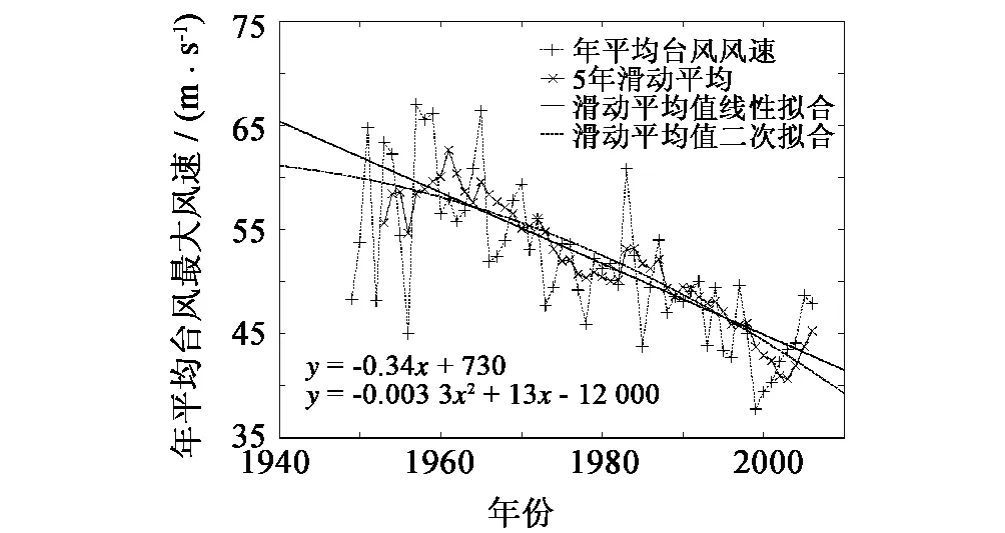
图5 年台风风速及5年滑动平均Fig.5 Typhoon frequency and 5-year running average

图6 年台风风速及10年滑动平均Fig.6 Typhoon frequency and 10-year running average

比较图5和图1、图6和图2中滑动平均值，能够看到台风发生频数多的年份台风强度也比较大，台风发生频数少的年份台风强度也相对的较小。也就是说每年台风发生的频数和强度可能有着相同的趋势。

使用Spearman秩次相关非参数趋势分析法算得rs=-0.703。查秩相关系数检验临界值表得P(rs≤-0.306)=0.01，所以拒绝原假设，认为年台风强度和时间成负相关性。即在过去的半个世纪里随着年份的增加台风强度呈减小的趋势。

图7 影响我国台风强度的R/S分析结果Fig.7 Typhoon strength＇s R/S analysis

下面利用R/S方法进行分析。仿照上面的第2步，把年台风风速从小到大排列，选取以累计频率25%的点作为分割点，风速小于等于分割点的年份看作台风强度较弱的年份。即把年平均台风风速不高于47.8 m/s的年份看作台风强度较弱的年份。这些年份是:1956，1973，1978，1985，1988，1993，1995，1996，1998，1999，2000，2001，2002，2003，2004。经过计算，得到H=0.212 8。在对数坐标中画出(ln(i)，R(i)/S(i))，并用线性拟合，结果见图7。H＜0.5，说明未来是反持续性的，将来的趋势与过去相反，也就是说未来影响我国台风的强度在R/S分析下呈现增大的趋势。

4 年极值台风强度的R/S趋势分析

同样的，结合上面的分析方法，对每年强度最大的台风产生的风速进行处理，如图8，并对年最大风速进行了10年滑动平均，可以看到呈现很明显的下降趋势。

图8 年最大台风风速及10年滑动平均Fig.8 Typhoon frequency and 10-year running average

使用Spearman秩次相关非参数趋势分析法算得rs=-0.824 1。查秩相关系数检验临界值表得P(rs≤-0.306)=0.01，所以拒绝原假设，认为年极值台风强度和时间成负相关性。即在过去的半个世纪里随着年份的增加年极值台风强度呈减小的趋势。

选取风速60 m/s为分割点，把年最大风速小于或等于60 m/s的年份看作年台风最大强度弱的年份。可得H=0.228 4。在对数坐标中画出(ln(i)，R(i)/S(i))，并用线性拟合，结果见图9。H＜0.5，说明未来是反持续性的，将来的趋势与过去相反，也就是说未来影响我国台风极值强度在R/S分析下呈现增大的趋势。这和上面预测的台风强度增强是一致的。

图9 影响我国年极值台风强度的R/S分析Fig.9 Annual extreme strength of typhoons＇R/S analysis

5 年台风强度和年台风频数关系

比较图4和图1、图5和图2中滑动平均曲线，能看到台风发生的频数多的年份台风强度也比较大，台风发生频数少的年份台风强度也相对较小。使用Spearman秩次相关非参数趋势分析法对此进行分析，算得rs=0.339 9，查表得P(rs≥0.306)=0.01，所以认为年台风强度和年台风频数之间呈现很强的正相关性。这点也是可以理解的，若某一年的气候很适合台风的形成，则台风发生的次数多，很显然这样的气候也利于台风强度的增大。

6 结语

1)先使用滑动平均的方法，对近58年影响我国的台风频数、强度和年极值强度进行趋势分析，又使用Spearman非参数趋势检验法进行了显著性检验。推断出近半个世纪里影响我国台风的频数台风强度和年极值台风都呈现下降的趋势。并且年台风频数和年台风强度有正相关性。

2)应用基于分形理论的R/S方法对未来的台风频数、强度和年极值强度进行了趋势预测。分析表明，未来影响我国的台风频数、强度、年极值强度呈现反持续性，将呈现增加增强的趋势。

这里只是从纯统计的角度对台风的发生趋势进行预测，无法从台风形成的机理上进行预测。还需要相关科研工作者进一步的研究。

［1］曹 楚，彭加毅，余锦华.全球气候变暖背景下登陆我国台风特征的分析［J］.南京气象学院学报，2006，29(4):455-461.

［2］董 胜，刘 伟，宁进进.台风波高重现值的泊松最大熵分布估计［J］.中国造船，2009(4):13-21.

［3］王莉萍，代 伟，齐 莹.设计波高推算的一种新模型［J］.中国海洋大学学报，2010，40(1):54-58.

［4］赵宗慈，江 滢.热带气旋与台风气候变化研究进展［J］.科技导报，2010，28(15):88-96.

［5］马丽萍.气候变化对热带气旋活动的影响［D］.南京:南京信息工程大学，2009.

［6］张 颖，王会军.全球变暖情景下西北太平洋地区台风活动背景场气候变化的预估［J］.气象学报，2010，68(4):539-549.

［7］王 星.非参数统计［M］.北京:中国人民大学出版社，2005:186-190.

［8］王静龙，粱小筠.非参数统计分析［M］.北京:高等教育出版社，2006:131-136.

［9］王孝礼，胡宝清，夏 军.水文时序趋势与变异点的R/S分析法［J］.武汉大学学报:工学版，2002，35(2):10-12.

［10］彭 云，苏春江，徐 云，等.径流丰枯时间序列的分型特征及R/S分析［J］.安徽农业科技，2007，35(1):4-5，8.

［11］樊 毅，周 芸，邹 玥，等.西南干热河谷降水蒸发变化趋势分析［J］.人民长江，2010，41(1):17-20.

［12］邱 林，黄 鑫，李洪良，等.基于模糊R/S分析方模型的降水预测在农业中的应用［J］.中国农村水利水电，2006，10:20-23.

［13］王 建，刘泽纯.全球变暖后西北太平洋台风频率的可能变化［J］.第四纪研究，1991，3:277-280.

Change trend forecast of frequencies and strengths of typhoons affecting China

LIU Tan-ran1，LIU Dong-xue2，XUE Dong-sheng3，WANG Jiong-jiong4
(1.College of Mathematical Sciences，Ocean University of China，Qingdao 266100，China;2.Zhejiang Surveying Institute of Estuary and Coast，Hangzhou 310008，China;3.Project Management Center，Offshore Oil Engineering Co.，Ltd.，Tianjin 300452，China;4.Network and Information Centre，Ocean University of China，Qingdao 266100，China)

The moving average is adopted to analyse the trend of the frequencies，strengths and annual extreme strengths of typhoons affecting China in the past 58 years.The Spearman rank correlation is adopted to conduct significance tests.Then we forecast the future trends of frequencies，strengths and annual extreme strengths of typhoons by Rescaled Range Analysis based on fractal theory.The results show that the frequencies，strengths and annual extreme strengths of typhoons affecting China will increase and become stronger.And there is a positive relation between annual frequencies and strengths of typhoons.

typhoon;moving average;Spearman trend test;R/S analysis

P444

A

1005-9865(2012)03-0170-07

2011-04-19

国家自然科学基金资助项目(40876094)

刘坦然(1986-)，男，山东潍坊人，硕士生，主要从事数理统计、数字信号处理和分析研究。E-mail:liutanran33@163.com