DELFT 3D在离岸人工岛建设中的应用——以海南岛万宁日月湾人工岛为例

龚文平，李昌宇，林国尧，莫文渊

(1.中山大学海洋学院，广东广州 510275;2.海南省海洋开发规划设计研究院，海南海口 570125)

DELFT 3D在离岸人工岛建设中的应用
——以海南岛万宁日月湾人工岛为例

龚文平1，李昌宇1，林国尧2，莫文渊2

(1.中山大学海洋学院，广东广州 510275;2.海南省海洋开发规划设计研究院，海南海口 570125)

离岸建设人工岛是围填海的重要方式之一。人工岛的建设势必改变工程区的水动力条件、泥沙输运格局与海岸演变状况。选取合理的平面布置方案，减少工程建设对海岸环境的负面影响，是人工岛建设能否成功的关键因素。以海南岛万宁日月湾人工岛建设为例，利用DELFT 3D模型系统，研究原场与不同平面布置方案后的波浪传播、波生流、泥沙输运与岸滩演变，探讨不同人工岛方案岛后形成连岛坝(Tombolo)或突出体(Salient)的可能性及泥沙淤积体积的大小，分析不同方案的优劣。研究表明，不同人工岛方案因为其大小、离岸距离及所处位置的差异，对岛后的波浪传播、波生流、泥沙输运与地形冲淤演变产生不同的影响。人工岛离岸距离越远、所处位置水深越大，人工岛在波峰线上的投影长度越短，形成连岛坝的可能性越小。

DELFT 3D;人工岛;连岛坝;突出体;海南岛

海上人工岛建设正成为土地资源相对贫乏的国家和地区开发利用海洋资源的重要方式之一［1］。目前国内对人工岛建设前后的潮流动力［2］、水体环境与水交换［3］、泥沙淤积［4］、对砂质海岸的影响［5］等都进行了较多的研究，但遗憾的是，研究中大多以考虑潮流及其输沙为主，对波浪作用的影响研究相对较少，即使是对砂质海岸。而国际上对人工岛(或离岸堤)建设后波浪动力、波生流、泥沙输运与地貌演变则进行了大量的研究［6-10］。比较有代表性的成果为DHI的软件系统MIKE21以及Delft Hydraulics开发的DELFT 3D。

日月湾位于海南省东岸万宁县境内的新梅乡附近，地理位置为北纬18°36＇以北至岸边，东经110°12＇至110°14＇范围(图1)。其海岸地貌类型为岬角海湾地貌类型，两侧为由花岗岩基岩组成的岬角，海湾为呈弧形的沙质海岸。沿岸输沙率不大，初步计算为20 000～30 000 m3/a。潮流含沙量与潮流输沙率较小［11］。沙坝物质来源主要为古海底物质，也有少部份来自海岸的侵蚀物质。

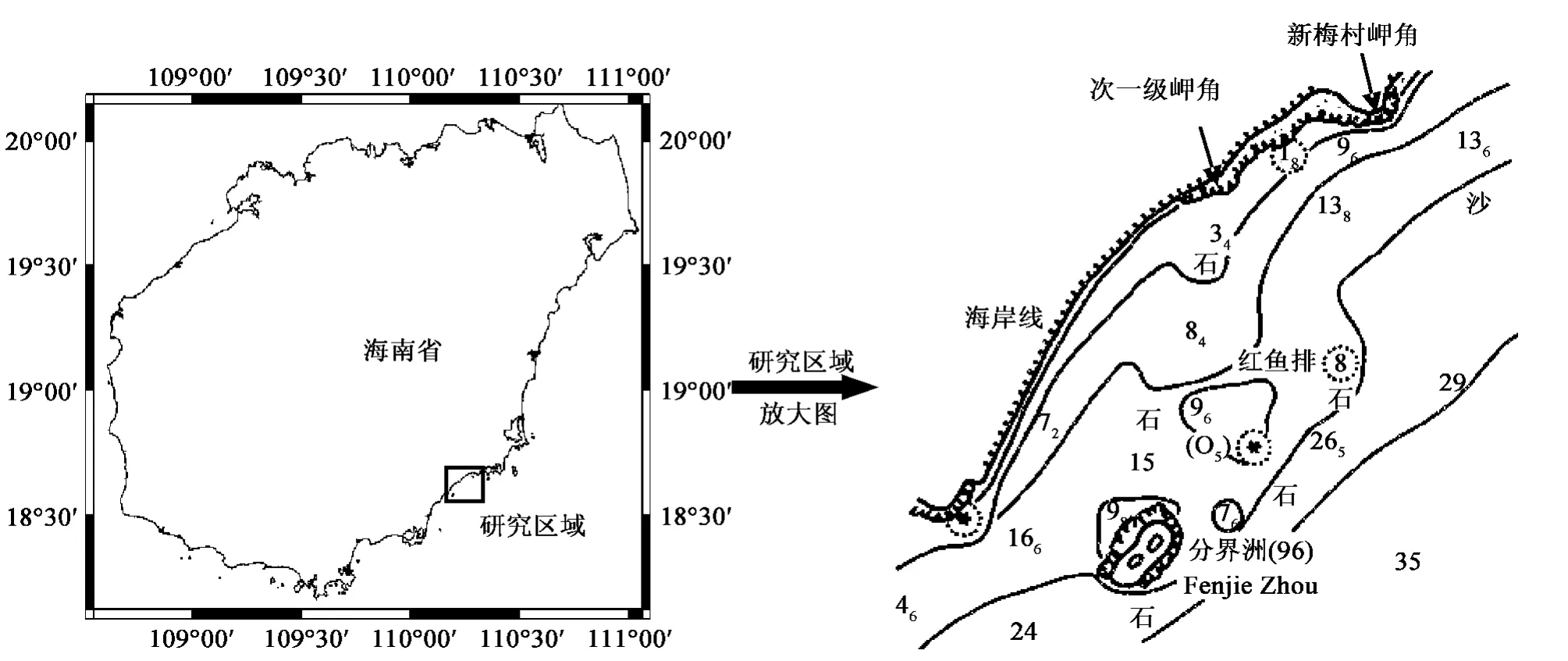
图1 日月湾地理位置图Fig.1 Geographic location of Riyue Bay

日月湾海域的主导风向是夏季的S向、SSW向和冬季的N向、NNW向。外海的波浪以风浪为主，常浪向和强浪向均为东南向，全年平均波高为0.91 m。潮汐类型为不正规全日潮混合潮型。年平均潮差为0.94 m，为小潮环境。海区潮流基本呈往复流特征，潮流流速在0.2 m/s以内［11］。涨潮流速大于落潮流速，余流方向基本指向偏东方向。根据Hayes［12］的海岸类型分类，日月湾为波浪作用为主的砂质海岸。

日月湾由于其良好的交通条件和区位优势，成为当地重点发展的区域。为进一步发展当地的旅游业，拟在日月湾内建设一人工岛(由状如太阳的日岛和状如月亮的月岛构成)。人工岛的平面布置方案是否合理是该项目成功与否的关键因素。为合理确定人工岛的平面布置方案，对原场与规划的三个人工岛方案进行了数值模拟计算，通过多方面的对比分析，确定出最优的建设方案。

由于国内对波浪作用为主的砂质海岸中人工岛建设前后的波浪动力、波生流及地貌演变的研究相对较少，本项研究一定程度上填补了该领域的空白，将丰富对砂质海岸动力地貌及人类活动影响的研究。

1 研究方法

1.1 数值模型

考虑到研究区的特色，采用DELFT 3D数值模型进行相关的数值模拟计算。

DELFT 3D［6］是一套耦合波浪、流、泥沙输运与地形变化的模型系统，其采用结构网格(矩形或曲线正交网格)，波浪模块利用SWAN 40.41进行计算，流模块与大多数的海洋环流模块类似，根据BOUSSNESQ假设，采用基本的连续方程与动量方程，以及标量的输运方程，计算水动力中的水位、流速、各种标量的浓度等。动量方程中包括了由波浪作用所产生的辐射应力和由波浪破碎产生的Roller而形成的动量项。

SWAN模型综合考虑了风能的输入，波浪的折射、绕射、破碎、底摩擦耗能、白浪、波-波相互作用等过程。SWAN也考虑了流对波浪的折射及频移(Doppler shift)的效应。DELFT 3D在模拟波流相互作用时，采用在线(ON-LINE)方式完成波-流交互作用。泥沙输运的计算在流场计算的每个时间步中进行。地形冲淤的更新则有自己的地貌时间步长，一般地形变化的时间步长要远大于流场的时间步长。

在本次研究中，采用DELFT 3D中的平面二维流场模型，其底摩擦系数采用谢才系数加以确定。对于波浪作用下的泥沙输运，模型采用的为VAN RIJN的SEDTRAN模块。对于地形的冲淤变化，DELFT 3D采用经过改进后的地形变化方程，在原有的欧拉方程基础上加进一扩散项，以保证计算的稳定性。DELFT 3D已经过良好的验证［6］，并在砂质海岸和淤泥质海岸的动力、泥沙输运与地貌演变模拟研究中获得广泛应用。

由于所研究区域范围相对较小，周围的河流径流量极小，斜压作用很次要，模拟过程中未考虑海水的温度、盐度、密度的时空变化，同时也未考虑风和次生流(Secondary Flow)对海岸过程的影响。由于潮流作用小，本次研究未考虑潮汐与波浪的相互作用。根据距离日月湾28 km、海岸走向与之基本相同的乌场湾的一年波浪实测资料，选取出现频率最大的三个浪向，即SE、SSE与SSW向，分别计算其平均浪与最大浪的向岸传播过程，以及这些波浪在向岸传播过程中产生的波生流和相对应的泥沙输运与地形冲淤变化及岸滩演变。

1.2 模型计算设置

根据不同的平面布置方案，生成了四套贴体的曲线正交网格，见图2。图中采用54坐标系及墨卡托(Mercator)投影，以m为单位。

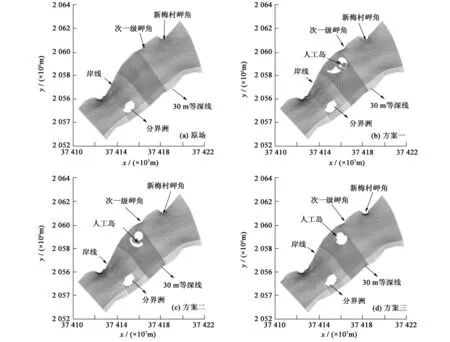
图2 模型网格图Fig.2 Model grid

网格的范围包括整个日月湾，西到分界洲附近，东至日月湾新梅村岬角附近，北以岸线为陆边界，南以海图中的30 m等深线为外海边界。网格单元数为162×99，网格的分辨率在外海边界区域相对较疏，而在岸线、分界洲岛以及拟建工程附近进行局部加密。为方便进行人工岛工程建设前后的比较，保持了网格的一致性，只是根据人工岛方案的不同，将人工岛所处的范围设置为岛边界。

将海图水深与工程区域附近1∶1 000地形图的水深数据统一到平均海平面下后，内插到模型网格中得到模型水深。

由于缺乏日月湾的海浪观测资料，采用距离日月湾只有28 km左右且海岸走向与日月湾基本相同、海浪特征完全可以代表日月湾近岸海域海浪特征的乌场湾波浪观测资料。根据1985～1986年乌场湾在10 m左右水深实测的波浪统计资料，选取出现频率最大的三个浪向SE、SSE与SSW向，分别将其平均波高采用简单的SNELL定律外推到外海30 m等深线处(除以折射系数与浅水系数)，得出如表1所示的计算边界条件。

对平均浪的计算，计算时间选取为3天。对风暴浪的计算，计算时间长度为1天。在波流相互作用过程中，选取FLOW子模块每计算120 min将流场与水位传送给SWAN进行波浪计算，即FLOW和WAVE的数据交换频率为120 min/次。模型的敏感性试验表明，选取不同的交换频率对模型结果无影响。在选取地形冲淤变化的放大系数时，在平均浪的情况下取为10，即1天的流场计算可得到相当于10天的地形变化结果，3天的平均浪计算可得到相当于30天的地形变化;而在风暴浪的条件下，因为一般风暴浪的作用时间较短，放大系数取为1，即不进行放大。风暴浪计算的地形变化为其作用一天的结果。

根据研究区的沉积物粒径分布［11］，模型中的沉积物粒径取为0.2 mm，为细砂至中砂。

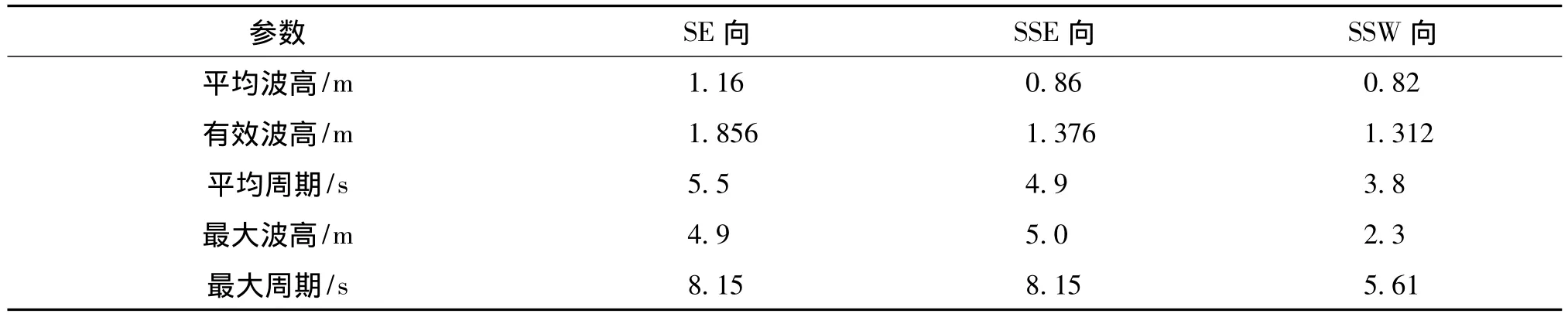
表1 计算边界条件Tab.1 Boundary conditions for computation

2 模拟结果及分析

根据上述初始条件，分别模拟SE向、SSE向和SSW向三个主要浪向下的平均浪和风暴浪自外海传播至日月湾海域的情形。

根据模拟结果，发现SSE浪的过程类似于SE向，而且其强度也较SE浪向为小。同时，无论从出现频率，还是波浪强度、产生的波生流、泥沙输运与地形变化来看，SSW向浪相对于SE向浪而言都很次要。下面只介绍SE浪作用的模拟结果。

在SE平均浪作用下，原场与三种不同设计方案的有效波高分布如图3所示。

从图3中可以看出:1)各个方案都会在人工岛岛后形成明显的波影区，但除了有效波高在岛后变化较大外，即由原场的1.6 m左右减小到岛后的0.5 m左右，其他区域则变化很小。同时，有效波高在岬角处变化梯度大，在海湾处则较小。2)方案一中，由于人工岛(日岛和月岛)之间的通道距离较大，加上通道近似于SE-NW走向，部分外海波浪可通过该通道传播到人工岛后，对岛后水域产生一定影响，具体表现在有效波高较其他两个方案稍大。

对波生流的研究表明(见图4)，在SE平均浪作用下:1)人工岛建设对分界洲岛后的水域和人工岛后东侧岸外海域有一定影响，但工程后流速大小和方向与原场的基本相似;2)不同方案下均会在人工岛后的西侧形成东向沿岸流，在东侧形成西向沿岸流。两股流在岛后汇聚，形成或大或小的一个或多个涡旋。而在方案一和方案二中，日岛的周围发育有一明显的逆时针绕岛环流。

从波生流的大小(见图4)来看，建岛后:1)波生流极大值较原场略有增大，由0.45 m/s左右增大到0.5 m/s左右，以方案一的增加值最大;2)分界洲岛后及人工岛后东侧新梅村岬角近岸水域为强流区域，但工程前后波生流相对大小基本无变化，说明人工岛的建设对该区域流速影响很小;3)人工岛后的近岸区域为强流区。

比较原场和三种方案在SE平均浪作用下泥沙输运情况(见图5)，可以看出:1)三种方案下的泥沙输运量值基本一样，但泥沙输运强度较原场略有增大，除了分界洲后西侧岸线以及新梅村附近岬角处岸线泥沙输移依然较大外，在岛后的东、西侧近岸区也出现较强的泥沙输运;2)人工岛后的东侧侵蚀，侵蚀泥沙在西向沿岸流输运下向岛后搬运，在岛后的东侧岸线附近形成淤积。人工岛后的西侧侵蚀，侵蚀泥沙在东向沿岸流作用下向岛后输运，但强度略小。方案一在人工岛后西侧的泥沙输运要略强于另外两个方案。

图3 有效波高分布Fig.3 Distribution of significant wave heights

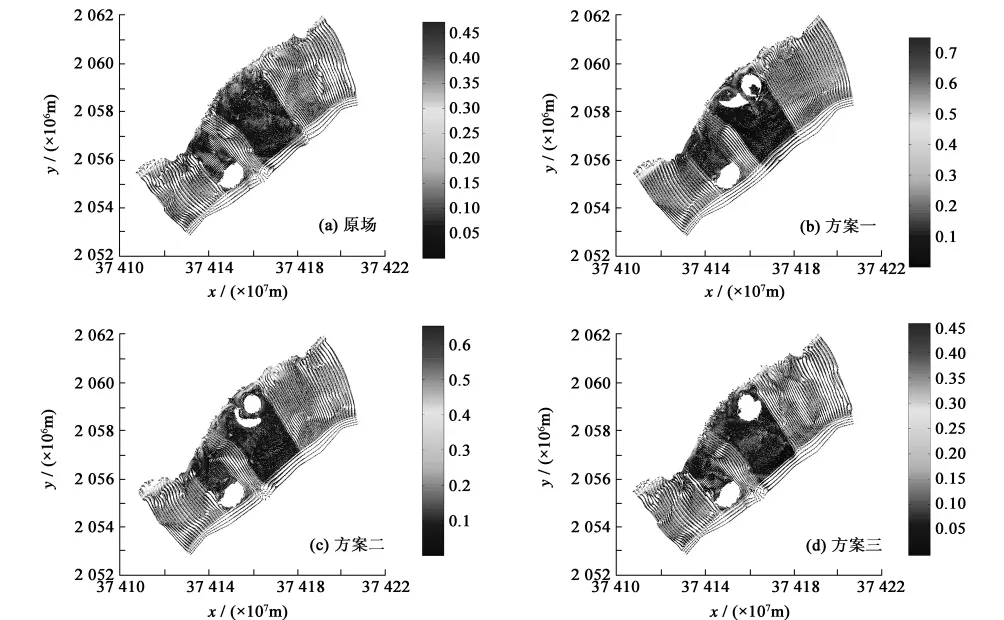
图4 波生流矢量与大小Fig.4 Wave-induced currents

再考虑到SE平均浪连续作用30天后造成的地形冲淤变化(图6)，可见:1)不论是原场还是人工岛三种方案，研究海域的大部分范围，特别是外侧海域，地形基本无冲淤变化。2)在原场时，沿着整个岸线附近都存在近岸淤积、岸外冲刷、再往外又淤积的冲淤相间的现象。人工岛建设后，岛后冲淤相间的格局不复存在。岛后东西两侧出现明显的淤积，且有向岛后发展的趋势。3)各方案中，方案一岛后的淤积速率和范围要明显大于另外两个方案。

图5 SE平均浪作用下的泥沙输运Fig.5 Sediment transport under SE mean wave

此外，对原场和三种不同方案进行了SE风暴浪条件下的模拟。相对平均浪，风暴浪的有效波高大小、波生流强度均为前者的2.5倍左右，而泥沙输移率则是前者的10倍，即要高出一个数量级。风暴浪作用下三种不同方案所产生的效果类似于平均浪下的情况，仅在波生流强度这一点上，方案一要稍大于另两个方案。关于SE风暴浪的作用效果不再赘述。

3 岸滩演变分析及最终方案的选定

对人工岛建设，一个备受关注的问题是建岛后是否会形成连岛坝或突出体。连岛坝出露水面，将人工岛与岸线相连，最终形成半岛(Peninsula)。而突出体则不能将人工岛与岸线相连。它们的发育将使岛后水域变浅，并可能影响旅游区有关功能的发挥。

国内外对人工岛或离岸堤(detached breakwater)建设后海岸的发育演变进行了大量的研究［13-18］，包括室内物理实验、野外长期观测(水动力、泥沙、岸滩剖面)、地形图与遥感图的对比分析、计算机数值模拟等，产生了大量研究成果。目前比较统一的观点是连岛坝的形成与波浪大小、泥沙供给条件、岛堤在波峰线上的投影长度B与其离岸距离X之比B/X有关。对于多个离岸堤，与相邻离岸堤之间的距离G也有关。当B/X越大，掩护的区域越大，掩护效果越好，岛后越易形成连岛坝或突出体;反之，则越难形成。为了便于说明问题，将三种方案下X、B和G的数值列表，见表2。

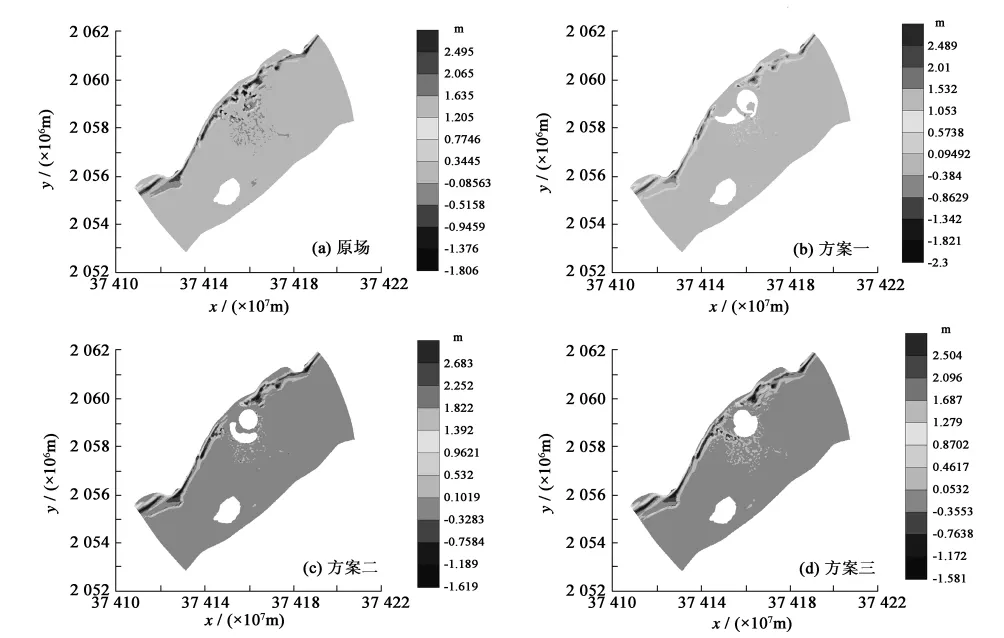
图6 SE平均浪作用30天后的地形冲淤变化Fig.6 Bathymetric change under SE mean wave for 30 days

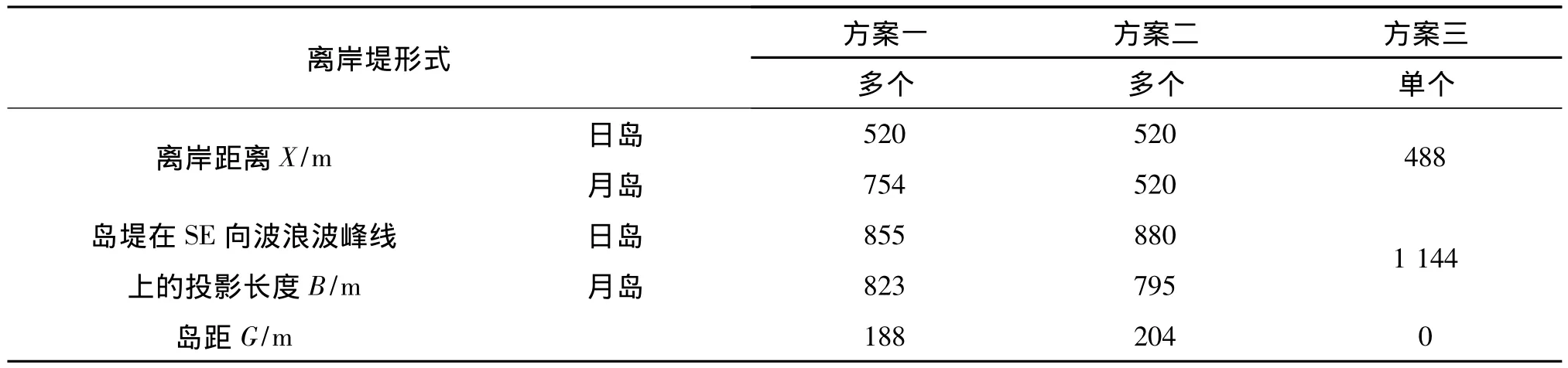
表2 三种方案下的离岸堤形式Tab.2 The parameters of three different detached breakwater schemes

1)Dally和Pope［13］提出，对于连岛坝的形成有如下判据:

其中，L为离岸堤处的波浪的波长，这里近似由等式L=1.56T2=47.19 m得到。

对于突出体的形成，不论是单个或多个离岸堤，其判据均为:

根据上述判据，对方案一而言，对日岛和月岛都有L=47.19≤G=188＜B。日岛的，易形成连岛坝;月岛的，则易形成突出体。

对于方案二而言，对日岛和月岛也都有L＜G＜B成立，日岛的，月岛的，故较易形成连岛坝。

2)Hallermeir［14］根据离岸堤所在水深大小，提出如下判据来判断是否会形成连岛坝:

其中:s为泥沙的密度，He为一年中出现时长不超过12个小时的深水波高，Te为该深水波对应的周期。采用万宁乌场湾一年实测资料中的最大SE波高与周期代入计算，得出dS为8.11 m。当离岸堤处的水深小于这一临界水深值时，连岛坝可能会形成。

按照此判据，在方案一中，日岛处的水深略小于该临界水深，而月岛处的则稍大于临界水深，因而有形成连岛坝的可能性;方案二中，日岛的位置与方案一的相当，而月岛的位置则略向外，形成连岛坝的可能性要小于方案一;方案三的人工岛处水深则大部分小于这一临界水深，会形成连岛坝。

3)Seiji et al.［20］得出离岸堤的间距与海滩演变的如下关系:

4)Suh 和 Dalrymple［18］得出结论为:

根据上面的分析，人工岛建设后，其后的海岸出现淤积是确定的。Wen and Ching［19］提出如下公式，计算离岸堤建设后，堤后的泥沙堆积的体积Qb满足:

对于多个的离岸堤:

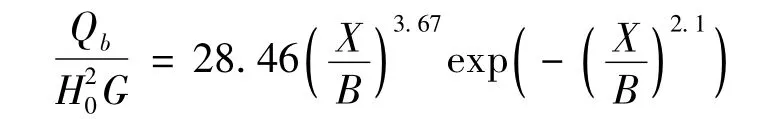
对于单个的离岸堤:

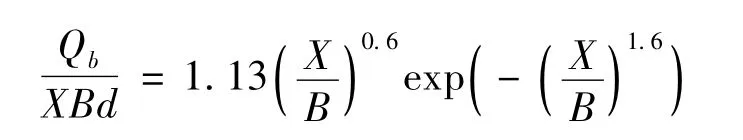
其中:d为破波处的水深，H0为离岸堤处的有效波高。由此计算，1)对于方案一，采用多个离岸堤的计算公式，工程建设后的泥沙堆积量为2 004.2 m3。如此小的泥沙堆积量可能偏小。2)对于方案二，工程建设后的泥沙堆积量为2 526.1 m3。量值也较小，但比方案一要大。3)对于方案三，工程建设后的泥沙堆积量为177 820 m3，如果按照年沿岸输沙率20 000～30 000 m3计算的话，则泥沙堆积体完全形成需要6～9年。

通过上述模拟和分析，可以看到方案一和方案二要明显优于方案三，但方案一、二之间孰优孰劣还不是很明确，为此，将SE平均浪条件下的计算时间延长，共计算10天，取地形变化的放大系数为10，得出SE平均浪连续作用100天的地形变化，相当于SE平均浪作用一年的结果(SE浪的出现频率为27.84%)。结果如图7所示。

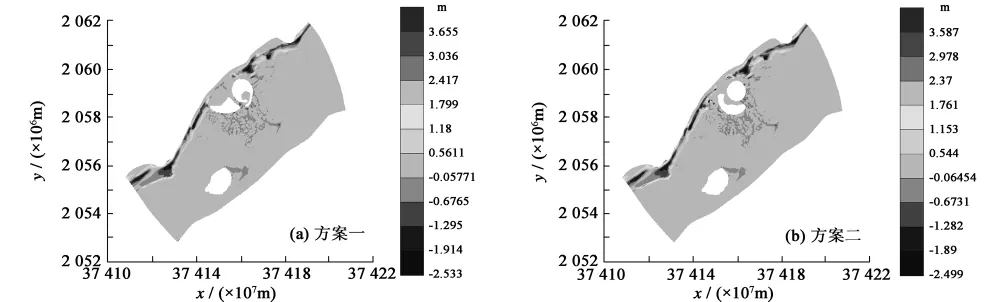
图7 方案一和方案二在SE平均浪作用100天后的地形冲淤变化Fig.7 Bathymetric changes of schemes 1 and 2 under SE mean wave for 100 days

从计算结果来看，SE平均浪连续作用100天后，方案一的日岛背后形成明显的淤积，淤积体离日岛的距离只有100 m左右，极有可能将日岛与岸线连接起来而成为连岛坝。在月岛的向岸侧也出现一定程度的淤积，但形成连岛坝的可能较小。而在日岛与月岛之间通道的向岸侧，则出现一定程度的侵蚀。对于方案二而言，在日岛的背后也形成淤积体，但淤积体离日岛的距离在180 m左右，淤积体将日岛与岸线连接起来形成连岛坝的可能性要小于方案一。方案二后在月岛的向岸侧也出现一定程度的泥沙淤积。

造成方案一与方案二这种差异的原因主要是由于两个方案中人工岛的尺寸不同。方案一后的波影区长，加上日岛与月岛之间波浪可以部分传入，不仅使岛后区域的波高沿岸梯度相对较小，从而形成的波生流也较小，而且传入的波浪还削弱了绕岛环流的发育，易于造成泥沙在人工岛周围的淤积。而方案二后的波影区相对较短，波高的沿岸梯度大，波生流强，绕岛环流也较强，因而泥沙的淤积幅度要小于方案一的情况。

根据以上分析，可认为方案二最优，其次为方案一。理由为:1)从其对波浪的屏蔽效果来看，各方案基本屏蔽了主要的三个波向的波浪，但方案一建设后日岛与月岛之间的通道内波浪仍可部分传入。2)从波生流的发育来看，方案一与方案二的日岛周围发育了良好的绕岛环流，水流通畅。方案二的环流要强于方案一。3)从地形变化来看，方案二在平均浪的作用下，其后的泥沙淤积相对较小，在风暴浪期间虽有一定的淤积，但整体上看是较优的;方案一其次。从计算的泥沙堆积体体积来看，方案二与方案一近似。根据数值模拟的结果，无论从短期(1～30天)还是中期(100天)来看，方案二建设后人工岛后的泥沙淤积相对最小。4)从能否形成连岛坝的角度来看，根据已有的经验公式(主要是离岸堤的长度与离岸距离之比)和中期数值模拟的结果，方案二形成连岛坝的可能性最小，其次是方案一。

4 结语

由于受时间和资料的限制，本次研究尚存在一定的不足，如SWAN本身仍不能精确模拟小尺度的港池、防波堤等海岸工程处的波浪绕射过程，也不能反映结构物对波浪的反射效应，因而不可能对人工岛前波浪的增强效应进行反映。另外，本次研究中进行的是平面二维的数值模拟，未考虑三维过程，因而对海滩剖面垂向上的波生流未能模拟，如在海滩演变中起重要作用的底流(undertow)就未被很好地加以再现，因而对风暴浪期间海滩的上部侵蚀不能反映。此外，也没有对波浪作用下岸滩的长期演变进行细致的模拟，有待在今后的工作中加强。

主要结论如下:

1)利用DELFT 3D对原场和三种不同的建岛方案分别进行模拟，从有效波高、波生流分布、泥沙输运、地形冲淤变化的结果比较了人工岛各种平面布置方案的优劣。

2)在不同方案下，由于日岛和月岛两者的大小、离岸距离及相对平面位置的不同，人工岛后方的波浪传播、波生流、泥沙输运与地形冲淤变化及岸滩演变会因此产生一定差异，岛后形成连岛坝或突出体的可能性也相应不同。根据短期(一天的风暴浪)、中期(30天至100天的平均浪)的数值模拟结果，结合已有的经验公式，判断表明，方案二的平面布置最优，其建设后形成连岛坝的可能性最小。

3)在设计和施建日月湾人工岛时，在考虑到经济效应、满足旅游区各项功能的前提下，日岛和月岛应尽量建在离岸线稍远、水深略大的区域，两岛间距也应适当，两岛的布局应尽量使其在波峰线上的投影长度最小。

［1］张名亮，吴伟强，陈 丽，等.江苏新月形人工岛建设探讨［J］.海洋开发与管理，2011，(3):30-33.

［2］郭 磊，杨树森.江苏如东人工岛工程对周边海域水动力的影响［J］.水道港口，2009，30(5):342-346.

［3］陆 敏，孙志国，孙大鹏.人工岛对海湾水环境影响数值研究［J］.海洋工程，2011，29(3):88-95.

［4］安永宁，吴建政，朱龙海，等.龙口湾冲淤特性对人工岛群建设的响应［J］.海洋地质动态，2010，26(10):24-30.

［5］岳娜娜，吴建政，朱龙海，等.离岸人工岛对砂质海岸的影响［J］.海洋地质动态，2008，24(4):18-22.

［6］Lesseer G R，Roelvink J A，van Kester J A T M，et al.Development and validation of a three-dimensional morphological model［J］.Coastal Engineering，2004，51:883-915.

［7］Nam P T ，Larson M ，Hanson H ，et al.A numerical model of beach morphological evolution due to waves and currents in the vicinity of coastal structures［J］.Coastal Engineering，2011，58:863-876.

［8］van Rijn L C.Coastal erosion and control［J］.Ocean＆Coastal Management，2011:doi:10.1016/j.ocecoaman.2011.05.004.

［9］Warner J C ，Sherwood C R ，Signell R P ，et al.Development of a three-dimensional，regional，coupled wave，current，and sediment-transport model［J］.Computers ＆ Geoscience ，2008，34:1284-1306.

［10］Zyserman J A ，Johnson H K.Modelling morphological processes in the vicinity of shore-parallel breakwaters［J］.Coastal Engineering，2002，45:261-284.

［11］海南省海洋开发规划设计研究院.海南岛万宁日月湾旅游开发自然条件可行性分析［R］.海口:海南省海洋开发规划设计研究院，1995.

［12］Davis R J，Hayer M O.What is a wave-dominated coast［J］.Marine Geology，1984，60(1-4):313-329.

［13］Dally W R，Pope J.Detached breakwaters for shore protection［R］.Technical Report，CERC 86-1，CERC.1986.

［14］Hallermeir R J.Sand transport limits in coastal structure design［C］//Proceedings of the Coastal Structure，ASCE.1983:703-716.

［15］Harris M M，Herbich J B.Effect of breakwater spacing on sand entrapment［J］.Journal of Hydraulic Research，1986，24(5):347-357.

［16］Hsu J R C，Silvester R.Accretion behind single offshore breakwater［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，ASCE，1990，116(3):367-380.

［17］McCormick M E.Equilibrium shoreline response to breakwaters［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，1993，119(6):657-670.

［18］Suh K，Dalrymple R A.Offshore breakwaters in laboratory and field［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，1987，113(2):105-121.

［19］Wen-Juinn C，Ching-Ton K.Effects of detached breakwater on shore protection［C］//International conference on Coastal and Port Engineering in Developing Contries.1995:246-252.

［20］Seiji W N，Uda T，Tanaka S.Statistical study on the effect and stability of detached breakwaters［J］.Coastal Engineering，1987，30(1):121-131.

Application of DELFT 3D model for plan design of an artificial island—A case study for the artificial island construction in the Riyue Bay，Wanning City，Hainan Island

GONG Wen-ping1，LI Chang-yu1，LIN Guo-yao2，MO Wen-yuan2
(1.School of Marine Science，Sun Yat-Sen University，Guangzhou 510275，China;2.Hainan Marine Development Plan and Design Research Institute，Haikou 570125，China)

The construction of offshore artificial island has become one of the dominant ways for land reclamation.It will definitely alter the hydrodynamics，sediment transport and coastal morphology in the surrounding area.A critical issue for the success of the project is to choose an optimal layout and minimize its negative impact on the regional environment.This case study focuses on the application of DELFT 3D model to the plan design of an artificial island in Riyue Bay，Wanning City，Hainan Island.Through simulation of the changes in wave propagation，wave induced circulation，sediment transport and morphological evolution under different layout schemes，the possibility of formation of tombolo or salient is discussed，and the potential accumulated sand volume is calculated.Consequently，the advantages and disadvantages of each layout scheme are compared，and finally，an optimal scheme is recommended.The study results show that the possibility of the formation of the tombolo is reduced as the artificial island becomes far away from the coastline，the location is deeper，and the projected length on the wave crest is shorter.

DELFT 3D model;artificial island;tombolo and/or salient;Hainan Island

TV148;U651+.4

A

1005-9865(2012)03-0035-010

2011-10-08

国家自然科学基金资助项目(40976052);国家海洋局公益项目资助课题(200905008)

龚文平(1968-)，男，湖北天门人，教授，主要从事河口海岸地貌动力学研究。E-mail:gongwp@mail.sysu.edu.cn

林国尧。E-mail:linguoyao63@163.com