摆式波浪发电装置一级转化效率模型试验研究

田育丰，黄 焱，史庆增

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

摆式波浪发电装置一级转化效率模型试验研究

田育丰，黄 焱，史庆增

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

一级转换装置是一个波浪能发电装置中的关键技术，而如何提高能量转化效率，是一级转换过程研究的重点问题。为确定一级转换装置的能量转化效率与哪些因素有关，对摆式波浪能发电装置的摆板机构进行了模型试验研究，测试了摆板模型在多种波浪条件下的动力响应参数，确定了摆板的动力输出特性及其控制因素;测试了在极限波浪作用下，摆板模型装置的受力状况。通过试验，为摆式波浪能发电装置的设计提供了必要的参考依据。

摆式波浪发电装置;能量转化效率;模型试验

面对石化能源危机和环境问题的巨大挑战，作为主要可再生能源之一的海洋能事业取得了很大发展。海洋能指依附在海水中的可再生能源，海洋通过各种物理过程接收、储存和散发能量，这些能量以潮汐、波浪、温度差、盐度梯度、海流等形式存在于海洋之中。其中，波浪能以其储量大、能量高、污染少、可再生等优点，越来越受到重视［1-5］。

摆式波能发电装置是利用摆板与波浪间的相互作用，摆板在波浪的作用下绕摆轴摆动，将波浪能转化为摆轴的机械能，通过与摆轴相连接的液压装置带动发电机发电。该装置由水室摆板机构、机电转换机构、发配电机构三部分组成。其中，水室摆板机构是一级转换装置，为了收集不稳定的波浪能，需要波浪能发电装置通过两级能量转换将波浪能中的机械能转化为我们可以方便使用的电能［6-8］。其中二级转换装置一般是普通的发电机，将机械能、液压能等转化为电能。而一级转换装置是一个波浪能发电装置中的关键技术，通过一级转换将不稳定的波浪能转化为稳定的、可用来带动发电机工作的机械能或液压能。一级转换装置工作的稳定性和对波浪能的转化效率决定了该波浪发电装置的能量转化效率、稳定性和经济性。而确定一级转换装置的能量转化效率与哪些因素有关，与影响因素间呈何种变化关系，如何提高能量转化效率，就成为对一级转换过程研究的重点问题。

针对上述问题，对摆式波浪能发电装置的摆板机构进行模型试验研究，测试摆板模型在多种波浪条件下的动力响应参数，确定摆板的动力输出特性及其控制因素;测试在极限波浪作用下，摆板模型装置的受力状况。通过试验，为摆式波浪能发电装置的设计提供必要的参考依据，为数值模拟分析提供验证数据。

1 模型试验

1.1 试验设施

试验在波浪水槽中进行。水槽长80 m，宽2 m，高2 m，两端分别设置造波系统和消波系统，如图1所示。

图1 波浪试验水槽Fig.1 The wave test channel

造波系统主要由机械装置、驱动装置和控制系统组成。机械装置主要包括推波板及其支撑和附属构件，波浪的产生是靠推波板往复运动来实现的，波高取决于推波板的行程和速度，波长则取决于往复运动的频率。驱动装置由交流伺服电机、滚珠丝杠和直线运动单元组成。控制系统对造波机运动的控制通过对伺服电机进行控制实现，通过工控机，根据设置的波浪参数计算造波机的时间序列控制信号，经D/A卡转换成模拟电压信号输出给伺服驱动器，控制伺服电机的转速和转向，实现造波机的运动调节数字化。造波控制过程中，其它辅助控制电路的反馈信号经控制采集卡输入到主控机中，以实现对造波机的智能化控制。

消波系统由两部分组成，即网格消波装置和斜坡式消波墙。网格消波装置布置在测试区域后20 m处，沿水槽高度方向布置两层间隔0.5 m、与水槽宽度相同的塑料网格。斜坡式消波墙设置在水槽的末端，这样造波系统生成的波浪，经过网格消波装置的二次消波与斜坡式消波墙的一次消波作用后，可达到忽略波浪反射对试验影响的效果。

1.2 相似准则

本文所进行的试验是一种流体模型试验，确切地说是一种液流模型试验，它要求原型液流和模型液流在力学上相似。力学上相似的两液流应当满足几何相似、运动相似、动力相似和边界条件相似。试验主要研究波浪对装置的作用，这种情况下，重力和惯性力是决定其受力的主要因素。因此模型试验中应满足弗劳德相似定律，即模型和原型的弗劳德数(Fr)相等，以保证模型和原型之间重力和惯性力正确的相似关系。此外，物体在波浪上的运动和受力带有周期变化的性质，模型和原型还必须保持斯特劳哈尔数(Sr)相似。由此可建立本次试验的相似体系，模型和原型中对应物理量的比尺如表1所示。

1.3 试验模型

试验模拟原型为靠岸式波浪发电装置，装置由水室、摆板、摆板轴等部分组成。摆板轴的轴承座固定在水室的侧墙上，摆板可以绕摆轴转动。在波浪的作用下，摆板绕摆轴前后摆动，从而将波浪能转化为摆轴转动的机械能。摆轴的机械能通过液压系统，带动发电机发电。

表1 主要物理量相似比尺Tab.1 The main scaled physical factors

试验中，考虑造波水槽中可能出现的边界效应以及实际的造波能力，将物理模型的几何比尺确定为1∶10。水室模型结构由侧墙、后墙、底板和聚波喇叭口组成(见图2)，材料为红松，并经浸油防水处理。其中，为观测聚波装置对波浪能转化效率的影响，聚波喇叭口设计为可组合构件，这样试验中，依次对安装和不安装聚波喇叭口装置的模型结构进行了测试，分别命名为模型1试验和模型2试验。

摆板模型的尺寸在图3中给出。摆板模型由铝板及松木组合而成，摆板摆臂的上端固定于摆轴上，摆轴模型系铝质，通过滚动轴承安装在水室侧墙的支墩上。摆板结构总质量为4.67 kg，为考察摆板质量分布变化对波浪能转化效率的影响，试验中进行了两种纵向重心位置的摆板测试，分别命名为摆板1试验和摆板2试验。摆板1试验重心位置:z1=360 mm;摆板2试验重心位置:z2=230 mm。摆板纵向重心位置的改变靠调整摆板上配重滑块的位置实现。

图2 水室模型结构图(单位:mm)Fig.2 Sketch of the water room(mm)

图3 摆板模型结构图(单位:mm)Fig.3 Sketch of the pendulum model(mm)

摆式波力发电装置中，发电装置施加给摆轴的阻力称为负荷阻尼。为研究负荷阻尼对能量转换效率的影响，须人为地改变负荷阻尼的量值，为此，需要有施加并改变负荷阻尼的装置。

试验中，摆轴的一端与扭矩传感器通过螺栓紧密连接(扭矩传感器质量已计入摆板模型质量)，扭矩传感器另一端再以螺栓紧密连接铝环，使得铝环的周长较摆轴增大，在铝环外侧以环状皮质摩擦片包裹，该摩擦片以支架固定于水槽底面上。环状摩擦片一端固定，另一端连接细钢丝，钢丝通过滑轮伸出水槽外可悬挂重物。当悬挂重物进行加载时，摩擦片抱紧，摆轴转动阻尼增大，重物质量增加时阻尼也随之增大。当无重物加载时，摩擦片松开，摆轴转动阻尼可忽略不计。采用改变加载重物质量来调节负荷阻尼的方法可以使阻尼近似线性变化，方便在试验中调节负荷阻尼的大小，从而研究负荷阻尼对能量转换效率的影响。试验模型设置在距造波板40倍试验最大波长的位置，而试验中的有效试验波数为30个，从而可避免装置和造波板之间造成的多次反射对试验结果的影响。

1.4 测试系统

试验中共布置了17个传感器，其中包括:1个扭矩传感器、1个转角传感器、10个波压力传感器、2个测力传感器和3个波高仪。扭矩传感器的一端与摆板摆轴相连，另一端受负荷阻尼施加系统的控制，这样扭矩传感器将在与摆轴一起转动的过程记录摆板的转矩输出。摆板的摆角由转角传感器测量，转角传感器主要由旋转电位器构成，与摆轴的另一端紧密连接，随摆轴一起转动。为量测摆板在摆动中的受力大小，在摆板模型上安装了十个压力传感器。其中，五个安装在摆板的迎浪面，另五个安装在摆板的背浪面。迎浪面和背浪面的压力传感器布置见图3。两侧的轴承座通过测力传感器与水室模型连接，该测力传感器可同时纪录水平向和垂向受力情况。在波浪传播方向上沿程布置3个波高仪，其中两个在靠近摆板前方布置，用来测量波浪在传播过程中的波高变化。

1.5 试验条件

试验条件包括规则波和不规则波两项测试，由于篇幅所限，本文仅对规则波试验结果进行分析和讨论。试验中的波浪条件共包括:7种水深、8种波高和9种波周期，具体试验参数见表2。

表2 试验参数Tab.2 Test parameters

2 试验结果

试验中，摆板模型的动力输出特性是重点测试内容。摆板模型的动力输出特性包括:摆轴输出转矩随摆角变化情况、摆轴单周期内输出能量随摆角变化情况、各波浪条件下摆板波浪能的最大转化效率及对应转角。其中，摆板的能量转换效率指摆板输出的机械能与摆板宽度上的波浪能量之比。摆板输出的机械能由摆轴上的扭矩应变计和摆角电位器量测，摆板宽度上的波浪能量由计算求出。

摆板输出的机械能:摆轴上扭矩应变计测到的扭矩设为M(t)，摆角电位器测到的摆板摆角设为α(t)，取摆板竖直摆放时的摆角为零度，顺波向摆动时的摆角为正，逆波向摆动时的摆角为负，则一个波周期T内摆板输出的能量W为［9-10］:

一个波周期T内摆板宽度上入射波的能量为:

式中:ρ为水的密度;g为重力加速度;H为波高;B为摆板宽度;Cg为波群速度，由下式给出:

其中:ω为波浪圆频率;d为水深;K为波数，与波浪圆频率ω以及水深d满足色散关系:

这样，摆板的能量转换效率η可描述为:

由上述关系可得到不同工况(即不同水深、不同波高、不同波周期、不同负载)下，摆板的能量转换效率。

波浪试验开始前，首先采用静位移释放法，对摆板在空气中、零负载情况下的自由振动情况进行了测试，通过对其自振衰减曲线的分析得到了两种摆板的自振周期:摆板1为1.34 s;摆板2为1.12 s。这样，在波高70 mm、波周期1.26 s试验组次中，出现了摆板自身的动力特性与波浪周期相匹配的情况。以该波浪条件下模型1-摆板1试验中的纪录为例，对摆板模型的动力输出特性进行描述。

以该组试验中摆板摆动平均幅值为±6.75°时的试验为例，图4显示了摆角的时程，图5为转矩时程。由两条时程曲线可以清楚地看到，摆角与转矩在经历了初期大约10 s的小幅值波动瞬态响应段后，进入了稳定的较大幅值响应水平。

图4 模型1-摆板1试验转角时程Fig.4 The time history of swaying degree for model-I＆pendulum-I in one test

图5 模型1-摆板1试验转矩时程Fig.5 The time history of torque for model-I＆pendulum-I in one test

观察图4还可以看到，摆板的动力响应是一个由初始平衡位置向动力平衡位置过渡的过程。试验中，将摆板顺波浪作用方向摆动角度设为正值，逆波浪作用方向摆动角度设为负值，由此可见，在摆板进入稳态响应段后，摆板新的平衡位置出现在顺应波浪作用方向，即向后倾斜大约18°的位置上。摆板动力平衡位置的偏移，主要是由于摆板在行进波中沿波行进方向和逆波行进方向所受到的水动力阻尼具有显著的差别。

如前所述，为准确把握摆板的动力输出特性，试验中通过调整外加阻尼的方式实现了对摆板摆动幅值的控制，图6给出了摆轴输出转矩随摆角变化情况。可以看出，摆轴输出转矩随摆角的下降呈线性增长的趋势。将每种摆角情况下一个波周期T内摆板输出的能量W进行计算后，可得到W随摆角的变化趋势，如图7所示。

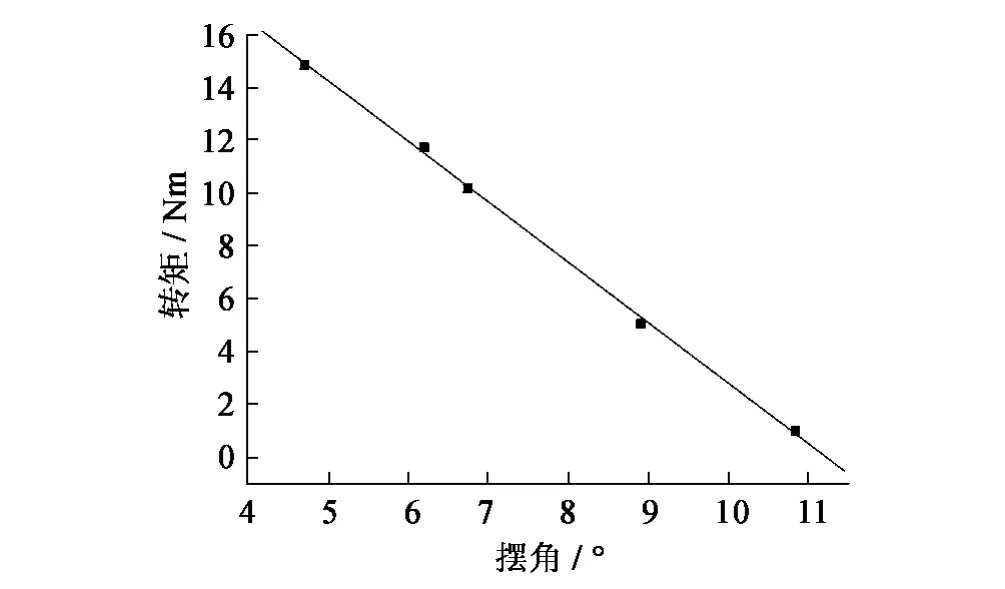
图6 模型1-摆板1试验转矩随摆角分布情况Fig.6 Plotted results of torque against swaying degree for model-I＆pendulum-I tests

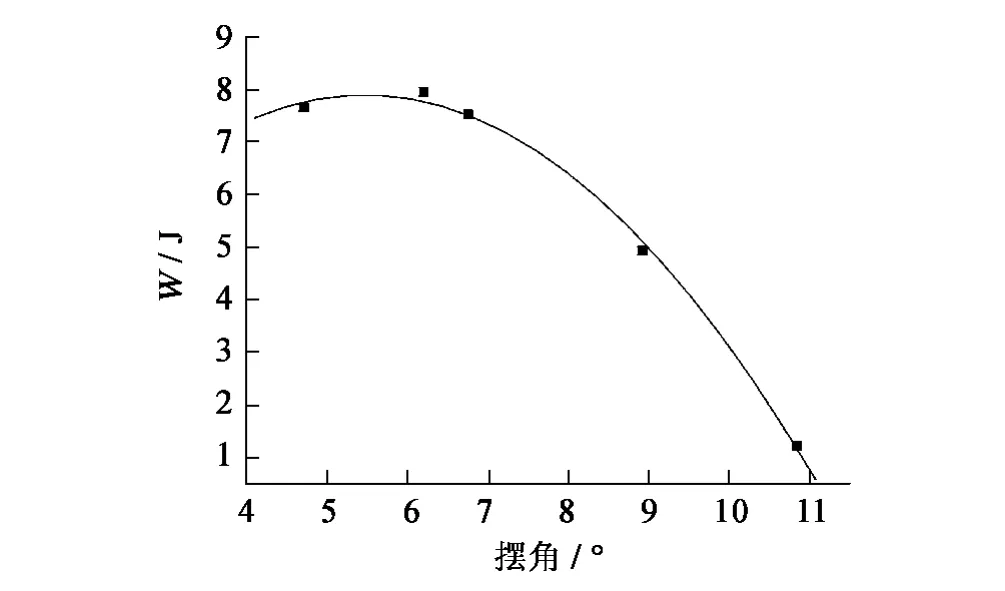
图7 模型1-摆板1试验输出能量W随摆角分布情况Fig.7 Plotted results of output energy W against swaying degree for model-I＆pendulum-I tests

由图7可以看出，一个波周期T内摆板输出的能量W随摆角呈二次曲线分布，图中的二次拟合曲线的方程可表述为:

式中:α为摆板摆动角度。对α进行求导，可推算得到该波况下摆板输出的最大能量值及其所对应的摆角幅值，分别为7.89J和 ±5.46°。

3 分析与讨论

3.1 聚波装置影响

喇叭口形状的结构形式之所以被认为具有聚波功能，主要是由于这种结构型式使得进入水室的水量增加，从而达到雍高水位加大波浪作用的目的。但聚波喇叭口的存在，同时对波浪形成了干扰，造成波浪在到达水室前首先受到较大的扰动，从而导致波形发生破坏。这样一来，就很难直接评价喇叭口是否具备积极的聚波功效。试验中发现，不同的摆板型式对喇叭口的影响具有不同的响应水平。

不同模型和摆板在水深345 mm下，试验的各波况最佳波浪能转化效率在图8中给出。可以看到，除波高125 mm的试验以外，模型1摆板1的波浪能转化效率在各波况下均为最高，当撤除聚波喇叭口结构后，即模型2摆板1，其波浪能转化效率大幅度降低，成为四种结构型式中转化效率最低的情况。由此可见，低重心的摆板对喇叭口的聚波功效最为敏感。同时，对于高重心摆板，即摆板2来说，波浪的规则作用对其转化效率的影响占主导地位，表现为摆板2在无喇叭口情况下的转化效率高于有喇叭口时的情况。这表明，喇叭口的聚波功效对于高重心摆板的影响是消极的。

同时还可以看到，尽管低重心的摆板在有喇叭口时的转化效率最高，对喇叭口的聚波功效也最为敏感，但喇叭口对波浪形成干扰所带来的影响也是很明显的。由图8可以看到，除模型1摆板1外，其他三种结构型式的最大波浪能转化效率分布具有较为一致的规律性，而在模型1摆板1情况下，这种规律性被打乱，尤其是在波高较小的情况下。

以波高175 mm的试验为例，图9给出了四种结构型式下的输出能量W随摆角变化的拟合曲线比较，从而可以更直观地反映上面的论述。

不同模型和摆板试验中结构的最大受力情况在表2中进行了汇总，结构受力包括摆板最大受力、摆轴最大水平力以及摆轴最大垂直力。可以看出，聚波喇叭口对结构受力状况的影响与对波浪能转化效率的影响是一致的，即模型1摆板1受力最大，而模型1摆板2的受力最小，其它两种结构型式的受力水平居于中间。

图8 水深345 mm各波况最佳波浪能转化效率分布情况Fig.8 Plotted results of the best energy converting efficiency against wave height in 345 mm water depth tests

图9 波高175 mm试验各模型W随摆角变化的拟合曲线比较Fig.9 Plotted results of W against swaying degree in 175 mm water depth tests

3.2 水深影响

试验中共考虑三种潮差，即100、200和250 mm，这样加上平均水位试验，共进行了7个水位的试验。每种水位均进行至少3种波况的测试，水室模型为模型1，摆板模型为摆板1和摆板2。图10和图11分别给出了两种摆板在不同水深情况下的最佳能量转换效率分布。

可以看到，对于摆板1，即低重心摆板来说，在波浪条件一致的情况下，水位越高，摆板的波浪能转化效率越高。导致这种变化规律的原因是显而易见的，水位越高，摆板在水中体积越大，从而受到的波浪作用越大，进而吸收并转化为机械能的波浪能比例也越大。同时值得注意的是，当波高为300 mm时，即便在最低水位345 mm时，波浪作用范围也覆盖了整个摆板，因此，摆板对波浪能的转化效率并不随水位有明显变化。

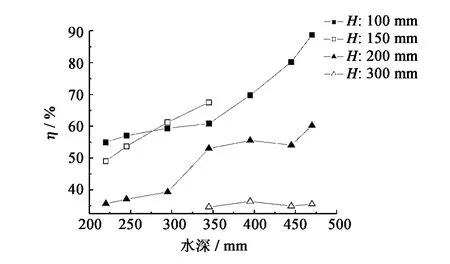
图10 摆板1各水深情况下的最佳能量转换效率分布Fig.10 Plotted results of the best energy converting efficiency against water depth for pendulum-I tests

图11 摆板2各水深情况下的最佳能量转换效率分布Fig.11 Plotted results of the best energy converting efficiency against water depth for pendulum-II tests

对于摆板2，即高重心摆板来说，在波浪条件一致的情况下，摆板1所体现出来的水位越高，摆板的波浪能转化效率越高的规律性不再出现，取而代之的是一种更为复杂的变化过程。这种变化过程体现为，对不同波浪条件来说，水位变化的影响具备不同的规律性。例如，当波高为100 mm时，规律体现为中间水位转化效率高，而高水位和低水位情况下转化效率均较低的变化趋势;而当波高为200 mm时，则出现了与摆板1截然相反的规律，即水位越高—摆板的波浪能转化效率越低的规律性。

由此可见，摆板2，即高重心摆板，对波浪的响应水平，也可描述为其运动情况受波浪的控制水平，明显低于摆板1，即低重心摆板。这是这样的特征，才导致摆板2动力特征的规律性表现为较为杂乱的特征。同样，当波高为300 mm时，即便在最低水位345 mm时，波浪作用范围也覆盖了整个摆板，因此，摆板对波浪能的转化效率并不随水位有明显变化。

图12 试验中的越浪现象Fig.12 The wave springing phenomenon in one test

3.3 波高与波周期影响

观察图8，还可以看到试验中最佳能量转换效率随波高的变化趋势。可以看出，在大部分试验中，尽管摆板的输出转矩和输出能量随波高成线性增长态势，但由于波浪能量密度随波高成二次增大的关系，摆板能量转换效率随波高的增大呈现下降的变化趋势。值得注意的是，当波高条件升至200 mm以上时，所有试验组次中均出现了越浪现象。这里所谓的越浪现象是指波浪作用经摆板传递后，水室内的水体跃出水室后墙。在部分试验中，水室内水体的飞溅高度甚至达到2 m以上，如图12所示。这种现象造成了大波高下摆板的能量转换效率出现突降。

试验中，针对波周期1.58 s情况下考虑了三种波高作用，即70、100和150 mm，水室模型为模型1，摆板模型为摆板1和摆板2。图13给出了两种摆板在同周期、不同波高情况下的最佳能量转换效率分布。从两幅图中同样可以看到，摆板能量转换效率随波高的增大呈现下降的变化趋势。

试验中，还针对波高100 mm情况下考虑了三种周期作用，即1、1.58和1.83 s，水室模型为模型1，摆板模型为摆板1和摆板2。图14给出了两种摆板在同周期、不同波高情况下的最佳能量转换效率分布。从两幅图中可以看到，两种摆板能量转换效率随波周期的变化趋势截然相反。由此可见，摆板2，即高重心摆板对短周期波更为敏感，而摆板1，即低重心摆板对长周期波更为敏感。

图13 同周期、不同波高情况下的最佳能量转换效率分布Fig.13 The best energy converting efficiency against wave height in constant wave period tests

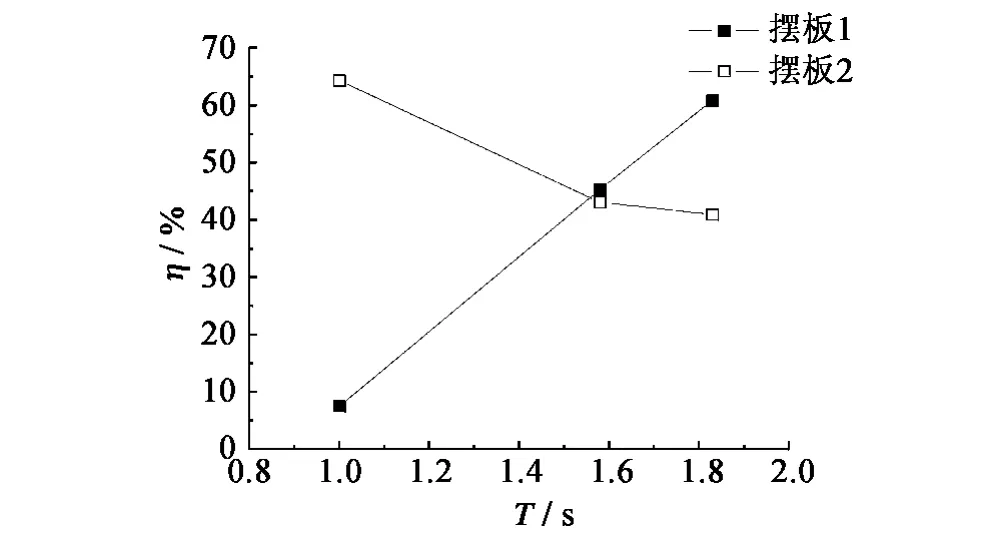
图14 同波高、不同周期情况下的最佳能量转换效率分布Fig.14 The best energy converting efficiency against wave period in constant wave height tests

4 结语

通过模型试验研究，可以看到，摆式波浪发电装置的一级转化效率受多种因素的影响控制。同时，通过前面进行的一系列分析还可以看到，摆板结构重心的不同会直接导致动力输出特性的变化，现将这两种摆板所体现出来的不同性质总结如下。

1)在大部分试验中，摆板1的波浪能转化效率均高于摆板2，由此可见，低重心摆板对波浪能的转化更有效;

2)模型1摆板1的波浪能转化效率在各波况下均为最高，当撤除聚波喇叭口结构后，即模型2摆板1，其波浪能转化效率大幅度降低，成为四种结构型式中转化效率最低的情况。由此可见，低重心的摆板对喇叭口的聚波功效最为敏感。同时，对于高重心摆板，即摆板2来说，波浪的规则作用对其转化效率的影响占主导地位，表现为摆板2在无喇叭口情况下的转化效率高于有喇叭口时的情况。这表明，喇叭口的聚波功效对于高重心摆板影响是消极的;

3)对于摆板1，即低重心摆板来说，在波浪条件一致的情况下，水位越高，摆板的波浪能转化效率越高。摆板2，即高重心摆板，对波浪的响应水平也可描述为其运动情况受波浪的控制水平，明显低于摆板1。

［1］T Stallard，R Rothschild，G A Aggidis.A comparative approach to the economic modelling of a large-scale wave power scheme［J］.European Journal of Operational Research，2008，185:884-898.

［2］Rhinefrank K，Agamloh E B，von Jouanne A，et al.A novel ocean energy permanent magnet linear generator buoy［J］.Renewable Energy，2006，31(9):1279-1298.

［3］Agamloh E B，von Jouanne A，Wallace A K.A novel direct-drive ocean wave energy extraction concept with contact-less force transmission system［J］.Renewable Energy，2008，33:520-529.

［4］N Sharmila，P Jalihal，A K Swamy，et al.Wave powered desalination system［J］.Energy，2004，9(11):1659-1672.

［5］K Paulsen，F Hensel.Introduction of a new energy recovery system-optimized for the combination with renewable energy［J］.Desalination，2005，184:211-215.

［6］Mats Leijon，Hans Bernhoff，Marcus Berg，et al.Economical considerations of renewable electric energy production-especially development of wave energy［J］.Renewable Energy，2003，28:1201-1209.

［7］Falcao A F de O.Control of an oscillating water column wave power plant for maximum energy production［J］.Applied Ocean Research，2002，24:73-82.

［8］Falcao A F de O.Modelling and control of oscillating-body wave energy converters with hydraulic power take-off and gas accumulator［J］.Ocean Engineering，2007，34:2021-2032.

［9］Kofoed J P，Frigaard P，Friis-Madsen E，et al.Prototype testing of the wave energy converter wave dragon［J］.Renewable Energy，2006，31:181-189.

［10］Huang Y，et al.Model test study of the interaction between ice and a compliant vertical narrow structure［J］.Cold Regions Science and Technology，2007，49:151-160.

Model test study of the primary energy converting efficiency of pendulum wave power device

TIAN Yu-feng，HUANG Yan，SHI Qing-zeng
(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

The primary energy converting equipments are the key technology in the wave power device.At the same time，the ways to enhance the energy converting efficiency are the core problems in the study of primary energy converting process.To identify the factors that control the energy converting efficiency of primary energy converting equipments，a model test study of the pendulum wave power device was performed.In these tests，the dynamic response of the pendulum model was measured.As a result，the dynamic output characteristics of the pendulum model and the key factors were revealed.At the same time，the loading status of the pendulum model in different wave conditions was also measured.The test results provide necessary references for the design of pendulum wave power devices.

pendulum wave power device;energy converting efficiency;model test

TK79

A

1005-9865(2012)03-0177-08

2011-10-10

国家自然科学基金创新研究群体科学基金资助项目(51021004)

田育丰(1986-)，男，黑龙江人，博士生，主要从事海洋工程专业研究。E-mail:2519200@163.com

黄 焱。E-mail:hjacyky@tju.edu.cn