某自动榴弹发射器刚柔耦合发射动力学仿真

徐 礼，毛保全，王传有，徐振辉

（装甲兵工程学院 兵器工程系，北京100072）

自动榴弹发射器是一种能自动装填、实施连发射击的榴弹发射器，口径通常在20mm以上[1].对自动榴弹发射器进行动力学仿真可以预测其动力学特性，验证机构的工作可靠性，为武器系统总体方案的论证和关键技术的突破提供理论依据.目前国内对弹链供弹的榴弹发射器进行动力学仿真的研究较少，弹链供弹机构的动力学仿真比较复杂，需要将弹链考虑为柔性体，并且仿真过程中有大量的接触/碰撞，加上自动机仿真过程中的接触/碰撞以及枪架腿杆柔性体，使得全系统的仿真难度增大，以往在对榴弹发射器的仿真研究中很少全面考虑此因素.文献[2]对QLZ87式35mm自动榴弹发射器进行了多刚体动力学仿真分析，文献[3]对某自动榴弹发射器进行了连发射击仿真，文献[4]对某单兵自动武器的榴弹发射系统进行了动力学仿真，并进行了供弹、抛壳分析.它们的研究对象都是弹仓供弹的榴弹发射器，并且采用多刚体动力学法进行仿真.本文以某弹链供弹的自动榴弹发射器为研究对象，考虑弹链及枪架腿杆的变形，运用ADAMS和ANSYS软件建立该榴弹发射器的刚柔耦合动力学模型，验证了模型的可信度，得到了该自动榴弹发射器的动态特性，研究了不同射角和自动方式对自动机运动特性的影响，分析了供弹机构的工作可靠性.

1 发射过程分析

该自动榴弹发射器口径为25mm，采用身管短后坐－导气混合式自动方式、前冲击发和弹链式单程供弹机构，自动机质量为3.66kg，活塞直径为28mm.枪机在枪管节套内回转闭锁，枪管下方装有导气装置，枪机安装在枪机框内，枪机框后部装有复进簧和缓冲簧，枪机框沿机匣往复运动，供弹机构及自动机结构原理如图1所示.

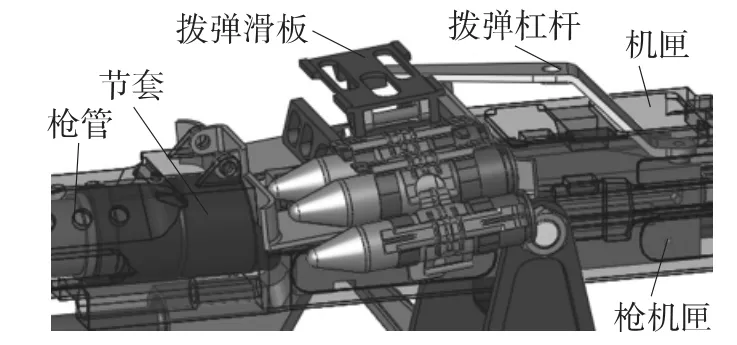
图1 供弹机构及自动机结构原理

扣动板击后，枪机框与枪机结合体在复进簧的作用下完成复进、拨弹、推弹等动作.枪机进入节套旋转闭锁，击针撞击底火击发弹丸，弹丸在火药燃气作用下向前加速运动，通过导气孔后，气室的火药燃气推动枪机框加速后坐，并带动枪机旋转开锁，完成抽壳、进弹、抛壳等一系列动作.枪机框后坐压缩缓冲簧并撞击枪尾，在缓冲簧与复进簧的作用下复进到达挂机位置，结束一个射击循环.若扳机处于连发状态，则枪机框以到达挂机位置速度为初始速度继续复进开始下一个射击循环.

2 刚柔耦合模型的建立

2.1 基本假设

根据该自动榴弹发射器的结构特点以及射击过程中自动机的运动规律，在不影响模型合理性的前提下，作如下假设：①武器系统中各构件（除弹簧、弹链和枪架腿杆外）均作刚体处理；②枪架支脚与地面固定不动；③弹簧内耗忽略不计.

2.2 多刚体模型的建立

该榴弹发射器主要由发射机构、供弹机构、机匣、自动机、枪管、枪尾等部件组成，运用三维建模软件SolidWorks建立各部件的实体模型，利用ADAMS与SolidWorks之间的数据接口将实体模型导入ADAMS中，然后根据各部件间的运动关系对模型进行简化，简化后全系统共39个刚体.

根据假设①，选择机匣为参照系[5].以枪口方向为x轴正向，以竖直向下为z轴正向，以左手准则确定y轴方向.按照系统内各刚体的实际运动和受力情况，分别添加相应的运动副和力元关系.机匣与枪架固定（枪架支脚与地面固定），与机匣直接连接的刚体有枪机框、受弹机座、受弹机盖等12个刚体，其连接关系如图2所示.其余刚体之间通过固定副、旋转副、移动副等运动副以及碰撞和弹簧等力元连接在一起，其中机心与其他刚体的连接关系如图3所示.

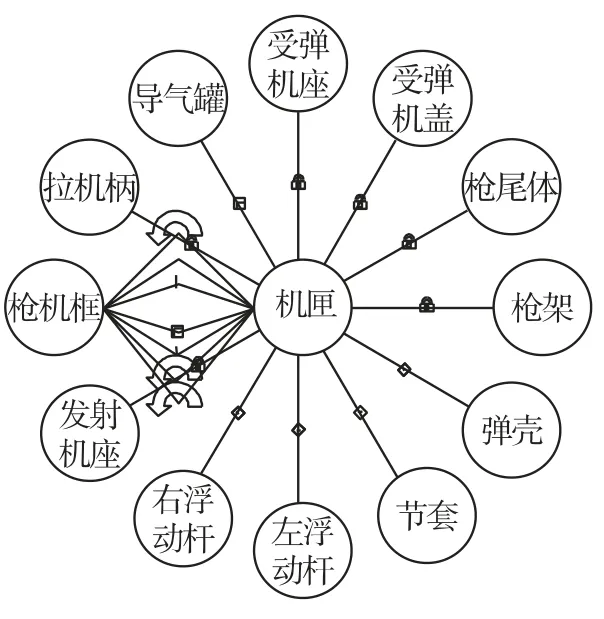
图2 机匣与其他刚体之间的约束关系

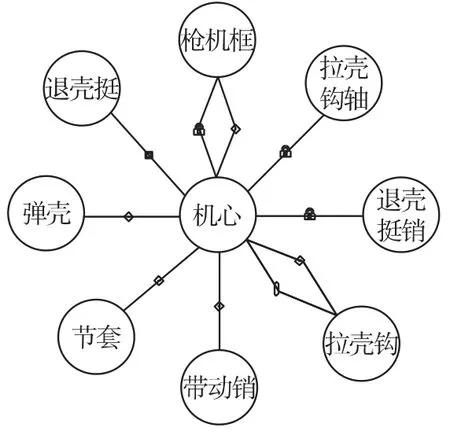
图3 机心与其他刚体之间的约束关系

模型中共15个固定副，12个移动副、10个旋转副、42个刚体碰撞.模型的总自由度：

D＝6×39－6×15－5×10－5×12＝34

2.3 柔性体模型的建立

供弹机构中，弹链的抱弹部分受到挤压变形.建模时，需要把弹链抱弹部分考虑为柔性体，弹链的其他部分仍可看作刚体.枪架系统中的3条腿杆的变形在武器射击时不可忽略，建模时也应考虑为柔性体[6].采用腿杆和弹链柔性体建立模型，使得仿真结果更符合实际.

ADAMS采用模态柔性来表示物体的弹性，运用模态中性文件来描述，本文采用ANSYS生成弹链和腿杆的模态中性文件，然后导入多刚体模型代替相应的刚体.替换后修改弹链抱弹部分与弹体之间的接触为柔性体与刚体接触.导入柔性体模态文件时，应与ANSYS中计算的模态进行比较，检查固有频率和振型是否相符，同时剔除影响不大的刚性模态[7].

引入柔性体后的弹链模型和枪架模型分别如图4和图5所示，枪架腿杆与发射器和地面之间都为固定约束.

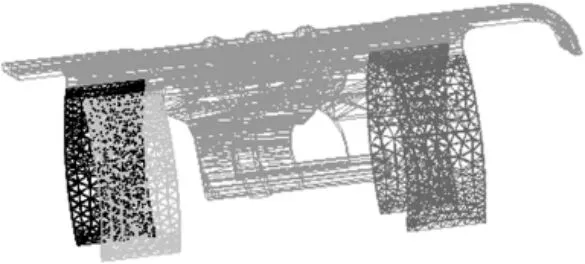
图4 弹链柔性网格模型

图5 枪架腿杆柔性网格模型

2.4 载荷参数的确定

自动机载荷参数是武器系统动力学模型的重要参数.考虑的载荷主要有抽壳阻力、膛底压力、导气装置中气室压力和各种弹簧的作用力等.

1）抽壳阻力. 根据设计要求，该榴弹发射器在膛压降为标准大气压时开始抽壳，抽壳阻力为[8]

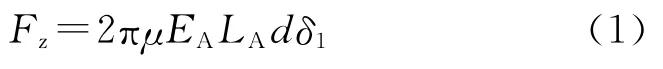
式中，μ为弹壳与弹膛之间的摩擦系数；EA为弹壳材料的弹性模量；LA为弹壳在弹膛内的总长；d为弹壳壁厚；δ1为弹壳与弹膛壁间的相对紧缩量.

根据试验测得δ1≈0.2mm，由式（1）计算得到抽壳阻力约为3 139N.仿真时，将该力施加到弹壳底部，力的作用时间为抽壳开始到弹壳离开弹膛的时长.

2）膛底压力. 考虑身管后坐，膛底压力分为从击发到弹丸运动至导气孔、弹丸从导气孔至飞出膛口和后效期3个时期，膛底压力可运用内弹道程序和布拉文经验公式计算得到[9].图6为内弹道压力－时间曲线.

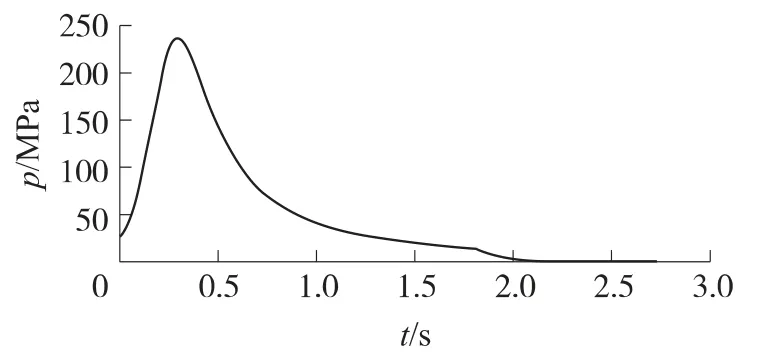
图6 内弹道压力－时间曲线

3）气室压力. 气室压力由布拉文经验公式计算[9]：

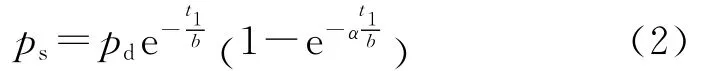
式中，ps为气室压力；pd为弹丸经过导气孔时膛内的平均压力；t1为弹丸经过导气孔开始计起的时间；α为导气装置结构尺寸参数，取α＝2.329 9；b为时间参数，取b＝6.826×10－4.计算得到气室压力－时间曲线如图7所示.

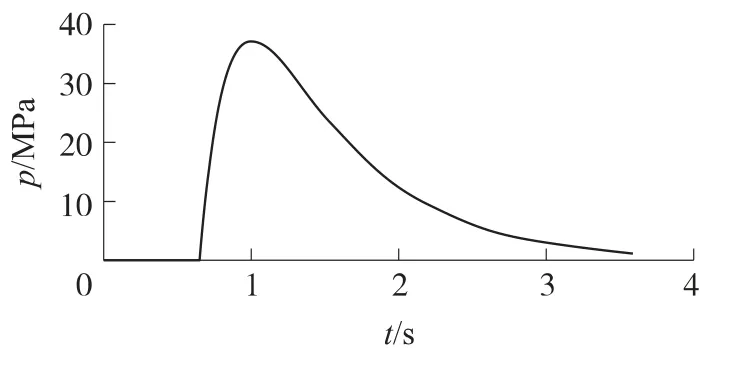
图7 气室压力－时间曲线

4）弹簧作用力. 该自动榴弹发射中的弹簧有复进簧、自动机缓冲簧、枪管缓冲簧和拉壳钩簧等压缩弹簧，还有拨弹齿簧和阻弹齿簧2个扭转弹簧.在ADAMS样机中，可以根据弹簧的设计刚度和预压力施加作用.主要弹簧参数如表1和表2所示，表中k1为压缩弹簧刚度，k2为扭转弹簧刚度，F0为预压力.

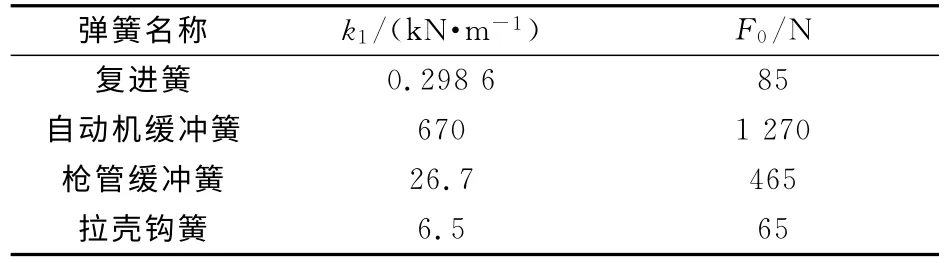
表1 压缩弹簧参数列表

表2 扭转弹簧参数列表

2.5 模型的验证

利用建立的刚柔耦合模型，对该自动榴弹发射器发射过程进行了仿真计算.选用0°射角射击时枪机框的速度、自动机缓冲簧最大受力和射频作为动力学模型的校核指标，仿真结果与试验结果对比，误差在10%以内，证明了该模型具有较高的可信度.实验测得的枪机框速度v′k曲线如图8所示，仿真结果与实测结果对比见表3和表4，其中vk和v′k分别为仿真和试验得到的各特征点时刻枪机框速度，Fmax为自动机缓冲簧最大受力，f为射频，e为相对误差.

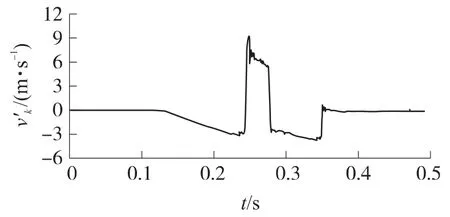
图8 实验测得的枪机框速度曲线

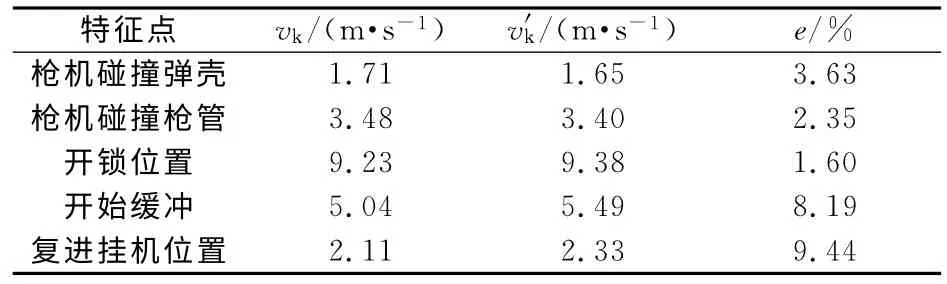
表3 枪机框速度仿真结果与试验结果对比

表4 自动机缓冲簧受力及射频的仿真结果与试验结果对比

3 计算结果分析

3.1 发射过程仿真分析

采用本文建立的自动榴弹发射器刚柔耦合动力学模型，进行三连发射击仿真计算，得到该自动榴弹发射器发射动力学特性.仿真时间从扣动扳机开始，射角为0°，仿真结果见图9～图16.

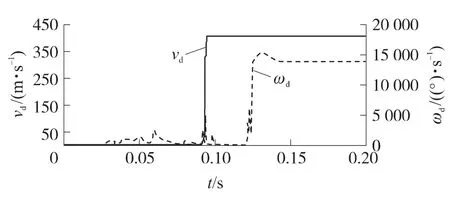
图9 弹丸质心的线速度和角速度曲线

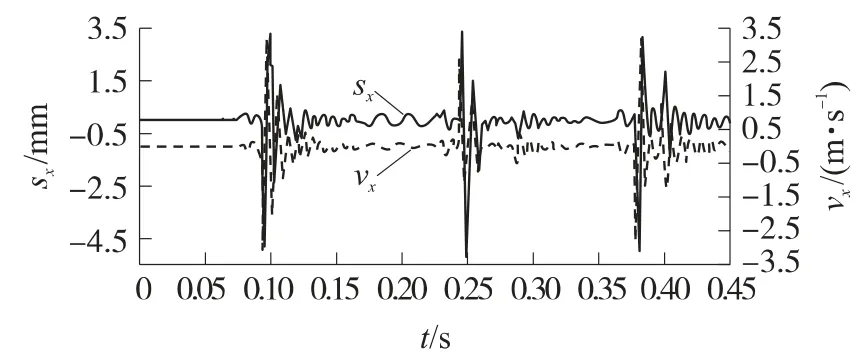
图10 枪口在水平方向的位移和速度曲线

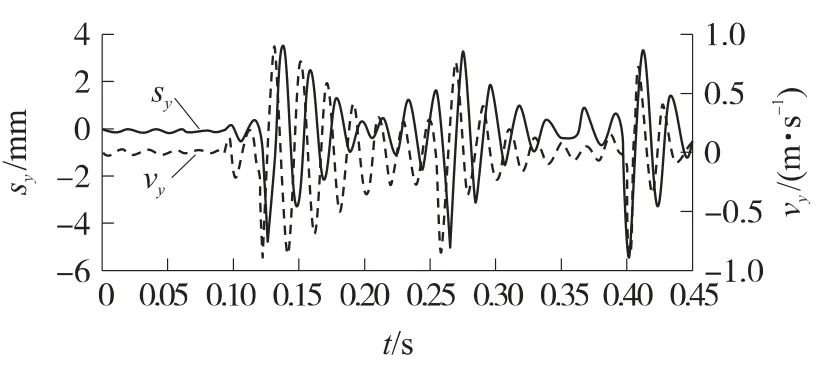
图11 枪口在高低方向的位移和速度曲线

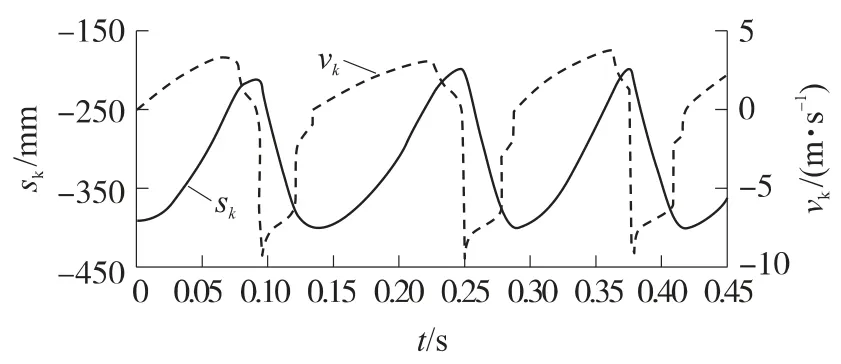
图12 枪机框质心在射击方向的位移和速度曲线

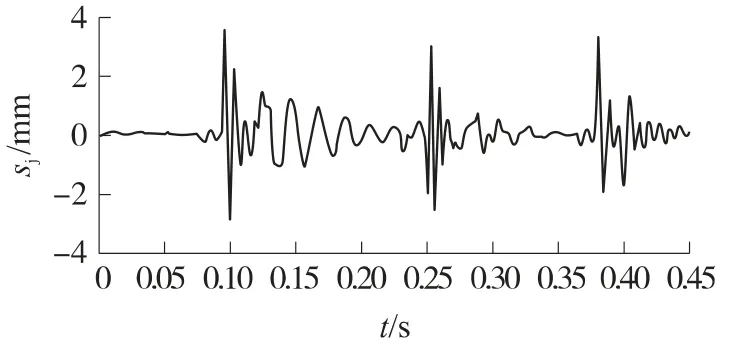
图13 摇架质心位移曲线

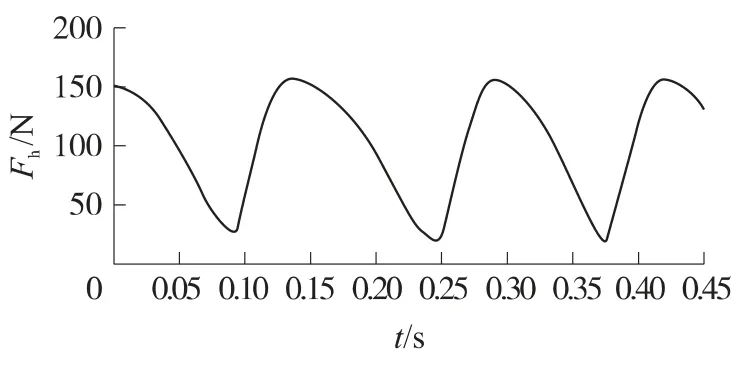
图14 复进簧作用力曲线

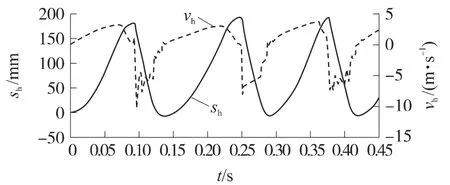
图15 复进簧变形和变形速度曲线

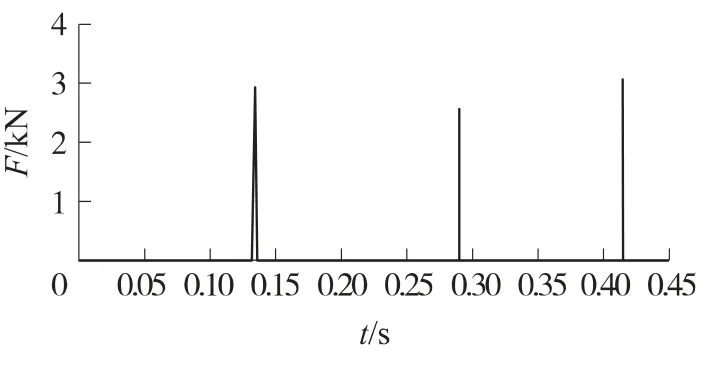
图16 自动机缓冲簧顶杆与枪尾碰撞的接触力曲线

通过仿真计算可知：①第1发弹丸出膛口的时间为0.095 2s，速度为407m/s，弹丸出膛口时水平向枪口位移为1.2mm，高低向枪口位移为1.7mm；②第1发射击时，自动机最大后坐速度出现在0.095s，最大后坐速度为9.15m/s，自动机后坐到0.118 2s时开始抛壳，此时自动机速度为4.98m/s，抛壳结束后自动机速度下降为3.31m/s，枪机框总行程为207.8mm；③由于摇架与柔性腿杆之间为固定连接，摇架质心位移综合反映了摇架与腿杆连接处的变形情况.

图14、图15分别为复进簧作用力Fh、变形sh和变形速度vh曲线，图16为自动机缓冲簧顶杆与枪尾碰撞的接触力F曲线.由第1发射击的仿真可知：在0.132 6s时刻自动机后坐到位，此时复进簧和自动机缓冲簧压缩量最大，枪尾受到复进簧作用力为156N，自动机缓冲簧顶杆对枪尾的碰撞力为2 931N.因此，自动机后坐到位时枪尾受力为3 087N，即复进簧作用力与自动机缓冲簧顶杆对枪尾的碰撞力之和.

3.2 射角和自动方式对自动机运动特性影响分析

1）不同射角对自动机运动特性影响分析.

在单发0°射角和30°射角2种情况下，分别仿真计算了自动机的速度，图17为2种射击条件下枪机框速度对比图.

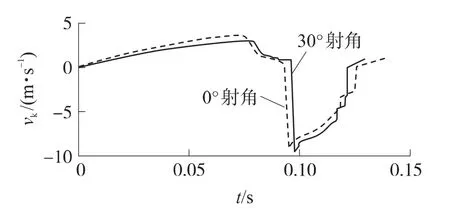
图17 0°射角和30°射角时枪机框速度对比图

该自动榴弹发射器的自动机质量比较大，在不同射角条件下，重力对自动机的运动特性产生一定的影响.当武器以正射角向上射击时，复进过程中自动机受到自身重力沿运动方向的分力，此力方向与自动机运动方向相反，将阻止自动机复进，使枪机碰撞枪管时的速度变小，延缓了击发的时间.由仿真可知，30°射角时枪机碰撞枪管的速度比0°射角时减小了0.61m/s，击发的时间延缓了3.73ms；后坐过程中自动机受到自身重力沿运动方向的分力，此力方向与自动机运动方向相同，将加速自动机后坐，后坐时间比0°射角时要短.由图17可知，30°射角单发射击的时间比0°射角单发射击的时间缩短了7ms，射频提高了22min－1.

2）不同自动方式对自动机运动特性影响分析.

该自动榴弹发射器为了在大口径、大威力条件下控制武器全重、保证武器在任何情况下都工作可靠而采用了身管短后坐－导气混合式自动方式.采用该自动方式可以将对武器机动性、射击稳定性和射击精度极为不利的第一冲量转化为自动机的工作能量.通过上述仿真计算可以看出，采用该混合式自动方式，自动机在不同射角下都有足够的能量完成各项动作，并且有一定的能量储备，能够保证武器在各种恶劣作战环境下都工作可靠.

在仿真过程中，可以把枪管体与机匣固定起来，使枪管缓冲装置不工作，从而使武器使用导气式的自动方式工作.2种不同自动方式下枪机框位移和速度对比分别如图18和19所示.

从图19中可看出，在其他结构不变的条件下，只采用导气式自动方式，自动机最大后坐速度为6.29m/s，比采用混合式自动方式小2.86m/s；由图18可知，自动机出现后坐不到位现象；由图20可知，只采用导气式自动方式时，弹壳经过抛壳点后，仍与枪机框有相同的速度，弹壳没有离开弹底窝，说明此时自动机速度较低而不能有效地抛壳.

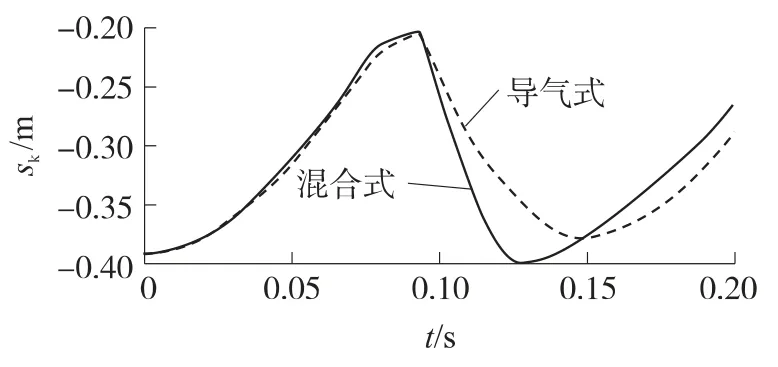
图18 不同自动方式下枪机框位移对比

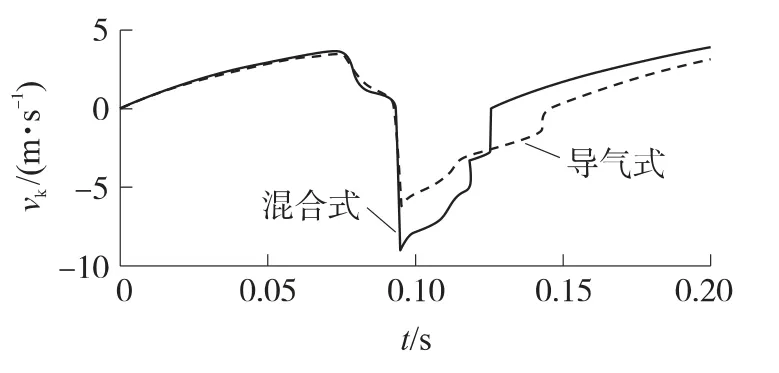
图19 不同自动方式下枪机框速度对比

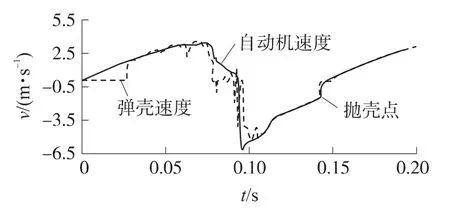
图20 导气式自动方式下弹壳速度与枪机框速度对比

3.3 供弹机构仿真分析

图21为拨弹滑板位移sb与速度vb随时间的变化曲线，图22为拨弹阻力Ft曲线.

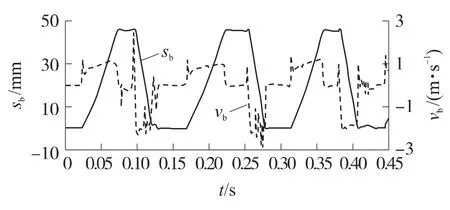
图21 拨弹滑板位移和速度曲线

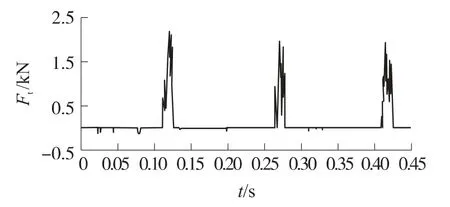
图22 拨弹阻力曲线

通过仿真可知，从0.024s时刻开始，拨弹滑板在拨弹杠杆的带动下滑动，直到0.075s时拨弹齿绕过待拨弹丸，拨弹滑板的行程为46.4mm.然后拨弹滑板保持在该位置，在0.097s时刻，拨弹滑板开始滑动，拨弹齿推动弹链到进弹口位置，该过程中，第1发弹丸在脱链齿的作用下被挤出弹链，最大拨弹阻力为2 203N.在0.123s时刻完成拨弹动作，拨弹滑板保持在此位置以待下一次供弹.

杠杆机构作为供弹传动机构时，拨弹滑板在起动和拨弹终了时速度有突变，拨弹杠杆和自动机上的曲线槽有一定的碰撞.弹链节距为43mm，拨弹滑板行程满足大于节距3～5mm的要求.

4 结论

本文基于ADAMS和ANSYS软件建立了某自动榴弹发射器的刚柔耦合动力学模型并进行仿真计算，并对其动力学特性进行分析，得到如下结论：

①该自动榴弹发射器的结构设计合理，将支架和弹链考虑为柔性体，建立刚柔耦合动力学模型，仿真计算得到的弹丸、枪管、自动机、复进簧和供弹机构等部件的动力学变化规律比较真实地反映了该榴弹发射器发射时的动力学特性.

②射角对自动机速度有一定的影响，大射角时自动机复进速度比小射角时的慢，但后坐速度快，总的射击时间缩短，射频提高.在进行复进簧设计时，应该考虑射角对自动机速度的影响，以保证不同射角下有足够的能量使自动机复进到位并且闭锁击发.

③该自动榴弹发射器的供弹机构工作可靠，能顺利地完成拨弹、进弹等一系列动作.拨弹滑板在起动和拨弹终了时速度有突变，但突变量不大，不影响供弹机构的工作可靠性.

[1]高国强，王红玲.步兵支援武器：自动榴弹发射器[J].现代军事，2002，（4）：18－20.GAO Guo－qiang，WANG Hong－ling.Infantry support weapon：automatic grenade launcher[J].Modern Military Affairs，2002，（4）：18－20.（in Chinese）

[2]高学峰.QLZ87式35毫米自动榴弹发射器动力学仿真分析与研究[D].南京：南京理工大学，2006.GAO Xue－feng.Analysis and research on dynamical simulation of QLZ87 30mm AGL[D].Nanjing：Nanjing University of Science and Technology，2006.（in Chinese）

[3]陈锦喜.基于ADAMS的某榴弹发射器虚拟样机仿真及其动力学特性分析[J].军械工程学院学报，2007，19（6）：42－45. CHEN Jin－xi.Dynamic simulation and characteristics analysis of the HE shell launcher with ADAM SP[J].Journal of Ordnance Engineering College，2007，19（6）：42－45.（in Chinese）

[4]赵彦峻，徐诚.某榴弹发射系统动力学仿真研究[J].系统仿真学报，2009，21（17）：5 450－5 453.ZHAO Yan－jun，XU Cheng.Research on dynamical simulation of individual soldier automatic weapon[J].Journal of System Simulation，2009，21（17）：5 450－5 453.（in Chinese）

[5]倪进峰.机枪系统虚拟样机建模及仿真分析[J].系统仿真学报，2005，17（8）：1 909－1 911.NI Jin－feng.Virtual prototype modeling and simulation analysis of machine gun system[J].Journal of System Simulation，2005，17（8）：1 909－1 911.（in Chinese）

[6]宫鹏涵，陈锦喜.某榴弹发射器刚柔耦合动力学建模与仿真研究[J].兵工自动化，2008，27（2）：46－48.GONG Peng－han，CHEN Jin－xi.Modeling and simulation for the rigid－flexible coupling dynamics of the automatic grenade launcher[J].Ordnance Industry Automation，2008，27（2）：46－48.（in Chinese）

[7]邢俊文.MSC.ADAMS/Flex与AutoFlex培训教程[M].北京：科学出版社，2006.XINGJun－wen.TutorialbookofMSC.ADAMS/Flex and AutoFlex[M].Beijing：Science Press，2006.（in Chinese）

[8]易声耀，张竞.自动武器原理与构造学[M].北京：国防工业出版社，2009：195－197.YI Sheng－yao，ZHANG Jing.Theory and structure of automatic weapon[M].Beijing：National Defense Industry Press，2009：195－197.（in Chinese）

[9]徐诚，王亚平.火炮与自动武器动力学[M].北京：北京理工大学出版社，2006：249－251.XU Cheng，WANG Ya－ping.Dynamics of artillery and automatic weapon[M].Beijing：Beijing Institute of Technology Press，2006：249－251.（in Chinese）