基于去虚二次多项式迭代的射角计算方法

贺 强，霍鹏飞

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

随着数字化技术的发展，战场节奏不断加快，需要缩短发射准备时间以提高快速反应能力，因此对火炮火控系统的实时性要求越来越高[1]。射角计算作为火炮火控系统中的重要部分，其计算效率直接影响了火炮火控系统的实时性能。

目前，射角计算方法主要有两类：一类是不计算弹道的射表迭代类，一类是计算弹道的数值积分类。数值积分类射角计算方法，是给定初始射角，计算射角对应的弹道得到落点，根据落点与目标点的差值不断迭代最终得到射角。因此弹道计算次数(并行计算的记为同一次)越少，射角计算效率越高。

随着计算机技术的发展，学者们提出了许多数值积分类射角计算方法。文献[2]提出采用二分法计算射角，文献[3]对二分法计算射角提出了一些优化措施。二分法虽然方法简单，但其弹道计算次数多，射角计算效率低。文献[4]提出了射角计算效率高于二分法的级数法。二分法和级数法都是串行计算方法。随着多核处理器在火炮火控系统中大量应用，学者们提出了射角计算效率更高的并行计算方法。文献[5]提出了改进遗传算法优化方法计算射角，其射角计算效率高于已有的串行计算方法。文献[6]提出了改进粒子群优化方法计算射角，该方法引入了周氏迭代修正公式，射角计算效率比改进遗传算法优化方法更高，但随着火炮火控系统对射角计算效率要求越来越高，其射角计算效率仍显不足。针对火炮火控系统对射角计算效率要求越来越高的问题，本文提出了基于去虚二次多项式迭代的射角计算方法。

1 改进粒子群优化方法计算射角

1.1 射程与射角关系简介

射程与射角关系示意图见图1。最小射角到最大射程角称为低射界，最大射程角到最大射角称为高射界。在低射界，射角增大，射程随之增大；在高射界，射角增大，射程随之减小。

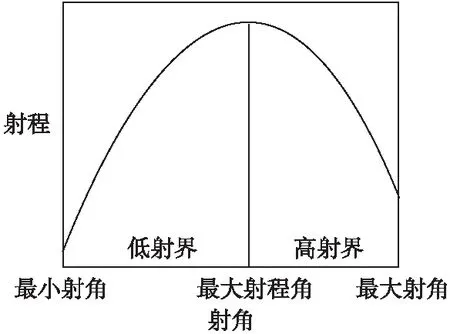
图1 射程与射角关系示意图Fig.1 Schematic diagram of the relationship between range and the angle of fire

1.2 改进粒子群优化方法计算射角简介

下面简单介绍改进粒子群优化方法计算射角的步骤：

1) 初始化

预估计射角θ0，然后在θ0附近随机生成N个粒子。

2) 评价粒子

为满足计算实时性要求，利用相对简单的4D弹道模型计算射程[7]。

计算N个粒子对应的射程，然后计算与目标射程的差值，将射程差作为粒子的适应值。采用周氏迭代修正公式得到修正的射角。根据适应值越小粒子位置越优的原则，更新粒子位置。

3) 粒子状态更新

根据更新公式对N个粒子进行更新。

4) 判断是否结束迭代

判断全局最优射角对应的射程差是否小于迭代截止误差。若小于，则迭代结束，全局最优射角为最终得到的射角。若不小于，返回步骤2) 继续迭代。

改进粒子群优化方法计算射角的具体步骤见文献[2]。

2 基于去虚二次多项式迭代的射角计算方法

观察图1可知射程和射角近似为二次多项式。但如果直接使用二次多项式迭代计算射角，存在数值解可能有虚部导致迭代中断的问题。通过比较发现数值解虚部的模值相对实部的模值很小，从数值迭代来说可以忽略，据此本文提出去除数值解的虚部，进行后续迭代计算射角，即基于去虚二次多项式迭代的射角计算方法。

基于去虚二次多项式迭代的射角计算方法步骤为：

1) 选取射角区间3等分的中间2个等分点和最大射程角θxmax作为初始点。

低射界取为：

(1)

(2)

θ3=θxmax

(3)

高射界取为：

(4)

(5)

θ3=θxmax

(6)

式中，θmin和θmax分别为最小射角和最大射角。

2) 采用并行计算，求出射角θ1，θ2，θ3对应的射程x1，x2，x3。

3) 采用二次多项式拟合，则

p0θ2+p1θ+p2=x

(7)

解得拟合系数为：

(8)

4) 迭代求射角的一元二次方程为：

p0θ2+p1θ+p2-xm=0

(9)

式(9)中，xm为目标射程。

一元二次方程解的判据为：

Δ=p12-4p0(p2-xm)

(10)

若Δ<0，则意味着数值解有虚部，此时令Δ=0即去除数值解的虚部。

5) 解得：

(11)

由于p0<0，式(11)中“±”在低射界取“+”，高射界取“-”。

6) 求出θn对应的射程xn。

7) 判断是否结束迭代。

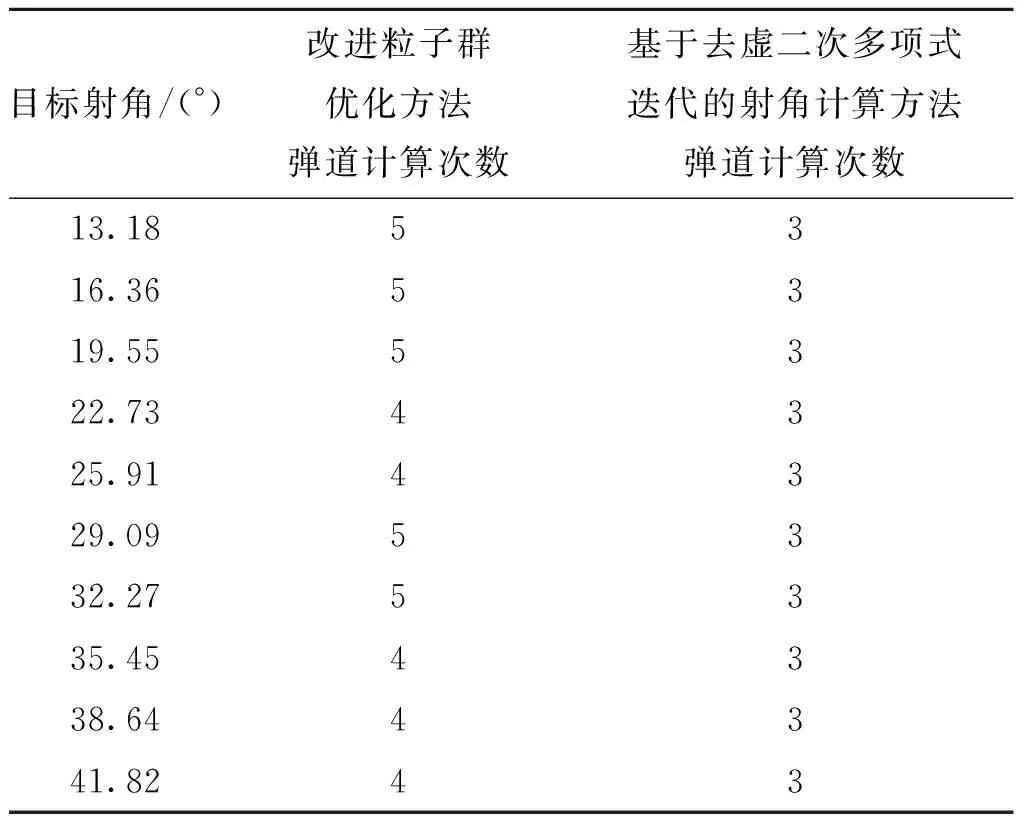
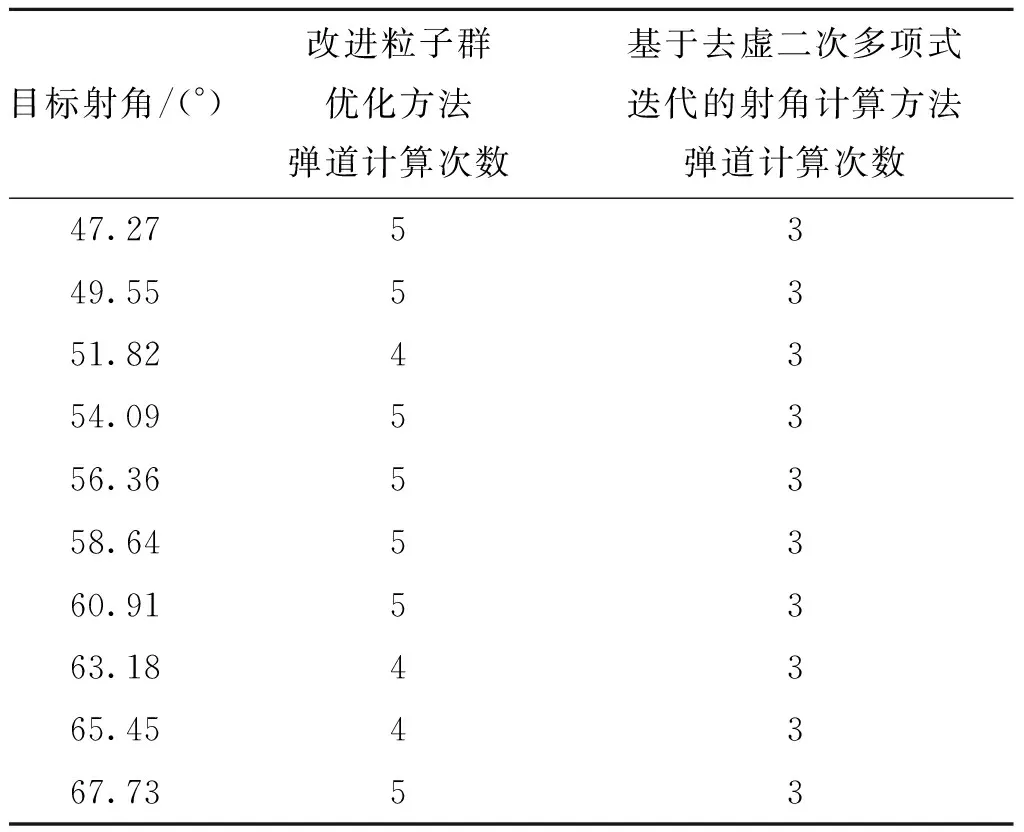
若满足迭代结束条件：|xn-xm|

基于去虚二次多项式迭代的射角计算方法采用并行计算3个初始点对应的射程提高计算效率，通过去除相对较小的数值解虚部，保证二次多项式迭代计算射角持续进行到迭代结束。

3 仿真验证

以122 mm底凹弹为平台，比较改进粒子群优化方法和基于去虚二次多项式迭代的射角计算方法的计算效率。仿真条件如下：处理器：4核i5 6500，内存：8 G，硬盘：500 G，操作系统：Windows7 64位，编程软件：Visud Studio 2010。

仿真模型与参数见表1。

在低射界，从10°～45°中均匀选取10个目标射角。计算出目标射角对应的射程作为目标射距，分别采用改进粒子群优化方法和基于去虚二次多项式迭代的射角计算方法计算射角。低射界弹道计算次数见表2。

表2 低射界弹道计算次数

在高射界，从45°～70°中均匀选取10个目标射角。计算出目标射角对应的射程作为目标射距，分别采用改进粒子群优化方法和基于去虚二次多项式迭代的射角计算方法计算射角。高射界弹道计算次数见表3。

表3 高射界弹道计算次数

弹道计算次数对比图见图2。

图2 弹道计算次数对比图Fig.2 Comparison diagram of trajectory calculation times

改进粒子群优化方法的平均弹道计算次数为4.6次，基于去虚二次多项式迭代的射角计算方法的平均弹道计算次数为3次。基于去虚二次多项式迭代的射角计算方法的射角计算效率在4核处理器硬件平台平均比改进粒子群优化方法高35%。

4 结论

本文提出了基于去虚二次多项式迭代的射角计算方法。该方法采用并行计算3个初始点对应的射程提高计算效率，通过去除相对较小的数值解虚部，保证二次多项式迭代计算射角持续进行到迭代结束。仿真验证结果表明，基于去虚二次多项式迭代的射角计算方法的射角计算效率在4核处理器硬件平台优于改进粒子群优化方法，平均高35%。