基于交错投影的无网格降维DOA估计算法
张子鑫,胡国平,周 豪
(空军工程大学,陕西 西安 710051)
0 引言
众所周知,DOA估计在雷达、通信等领域中起着非常重要的作用。传统的DOA估计算法主要有基于特征分解的多重信号分类(multiple signal classification, MUSIC)算法[1]和子空间旋转不变技术估计参数(estimating signal parameter via rotational invariance techniques,ESPRIT)算法[2]等。随着2006年Candes、Romberg等人提出压缩感知理论[3-6],突破了传统的奈奎斯特采样定理。压缩感知理论只需要少量的观测数据,同时利用信号在空域中的稀疏性,就能够有效进行信号重构,并且在相干信源的情况下,相比于传统DOA估计算法有着更好的性能。
但是传统的压缩感知DOA估计算法仍存在缺陷。即传统的压缩感知DOA估计算法利用了信号在空域中的稀疏性,需要将整个空域按照某种规则进行空间网格划分,将信号用所划分的网格点进行表示。而在实际的DOA估计中,信号在空域中是连续的,信号很可能不会恰好落在网格点内,而是落在两个网格点之间,这样就产生了网格失配的问题,称为基失配(basis mismatch)。在这种情况下很容易能想到通过增大空间网格划分的密度来解决,但是会导致基字典不满足等距约束(restricted isometry property,RIP)准则,导致信号重构的性能下降[7]。
对于此问题,有学者提出了基于偏离格点(off-grid)的DOA估计算法以及网格精炼的自适应网格算法,贝叶斯压缩感知也在这一领域得到了广泛应用。但是这些算法仍然是将空间进行网格划分,在提高测量精度的同时计算量也大大增加。对此,有学者提出了无网格(gird-less)DOA估计算法,此类算法能够利用测量值的原子范数的稀疏性来实现,利用原子范数来刻画信号特征,即通过在连续的空间中寻找最少的原子来表示信号,不需要对空域进行网格划分[8],能够在连续域中实现稀疏重构,因此不会出现基失配的现象。原子范数是由用于稀疏矢量估计的l1范数和用于低秩矩阵恢复的核范数推广而得到。原子范数的求解依赖于半定规划问题[9-11],即一个非光滑的凸优化问题,这使得原子范数可以有效求解。因此,无网格DOA估计可以通过求解秩最小化问题的凸优化进而得到一个半定规划问题来实现。但一般来说,凸优化问题存在复杂度高、收敛速度慢等问题。对此,文献[12]提出了一种可以直接求解半定规划问题的APG算法。该算法利用交错投影的方法将秩最小化问题中的矩阵迭代投影到对应集合当中来直接求解半定规划问题。但是APG算法直接求解的是秩最小化问题中的半正定矩阵,而不是DOA估计所需要Toeplitz矩阵,以至于算法存在收敛速度较慢的问题。本文针对此问题,提出了基于交错投影的无网格降维DOA估计算法。
1 基于无网格DOA估计问题求解
1.1 信号模型
假设有阵元数为M的均匀线阵,阵元间距为d,空域中有K个目标,它们的角度分别为θk,k=1,…,k,那么接收信号Y为:
Y=AX+N
(1)

1.2 无网格DOA估计
无网格DOA估计是通过利用一组测量值的原子范数中的稀疏性来实现的。原子范数最小化(atomic norm minimization, ANM)[13-15]已被广泛应用于各种各样的估计问题,包括DOA估计[16-17],而且在单个或多个快拍数的情况下都适用[18]。基于原子范数最小化的无网格DOA估计使用以连续变量t为特征的导向矢量a(t)作为原子集合:
α={A(t,b)=a(t)bH:t∈[-1,1),‖b‖2=1}
(2)
式(2)中,原子集合定义为所有约束范数的秩为1的矩阵的集合。该集合由一个导向矢量和任意测量值组成。因此,无噪声测量值Y的原子集合可以表示为:

(3)
若测量值中不含噪声,可以精确分解;若包含噪声,可以近似分解。文献[17]中解决了无网格DOA估计的原始非凸l0范数最小化公式,定义为式(4):
(4)
对于式(4)的求解可以转化为秩最小化问题来解决,即:
min rank(Toep(u))
s.t.S≥0
(5)
其中,
(6)
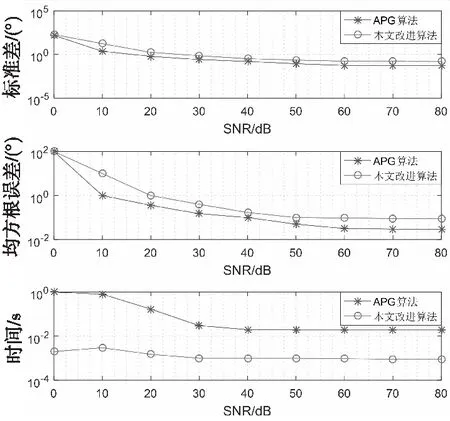
式(6)中,Z为自由变量且是一个共轭对称矩阵。Toep(u)是一个秩为K(K Toep(u)=VDVH (7) 交替投影是一种求两个或多个凸集合交点的基本算法。当所求的每个集合都是封闭的且是凸集时,用APG算法能够收敛到一个解。文献[12]在介绍APG算法之前,首先提出了几个重要的集合及矩阵在集合上的投影。 1) 秩约束集R,定义为: R={A∈CN×N:rank(A)≤K,K≤N} (8) 矩阵在集合R上的投影运算为: (9) 式(9)中,σk,[k=1,…,K]表示最大的前K个奇异值,uk和vk分别为左奇异矩阵和右奇异矩阵。 2) Hermitian Toeplitz矩阵集合H,矩阵在H上的投影是沿对角线元素的平均值参数化的Toeplitz矩阵: (10) 式(10)中,Ai,j和ui分别表示A和u中的元素。 3) 半正定集合P,定义为: P={A∈CN×N:λi≥0,∀i} (11) 式(11)中,λi是矩阵A的第i大的特征值。矩阵在集合R上的投影运算为: (12) 式(12)中,ei矩阵A第i大的特征值对应的特征向量。 4) 给定列空间的矩阵集合M。该集合是由给定K维列空间的N×M维复合矩阵组成。对于任何矩阵B∈M和A∈CM×P,P≥K,矩阵A在集合M上的投影运算为: PM(A)=BB†A (13) 式(13)中,B†为矩阵B的摩尔-彭若斯广义逆矩阵。 无网格DOA估计问题就是式(5)中对秩为K的Toeplitz矩阵的求解。因为一个半正定矩阵的所有子阵也是半正定矩阵且为对称矩阵,所以可得S,T(u),Z∈P,M。此外,还能够知道: rank(T(u))=rank(ADAH)=rank(A)=K (14) 因此,可以将式(5)、式(6)中的矩阵进行归类,具体归类如下: T(u)∈R,H,P (15) APG算法就是通过交错投影的方法将每一个矩阵迭代投影到相应的集合中来直接求解式(5),具体步骤如下: 步骤1 已知观测值Y∈CM×L,目标个数K个,判定收敛的界限ε。随机设定初始值: T0(u)∈CM×M,Z0∈CL×L 步骤5 对所求得的T(u)进行范德蒙分解T(u)=VDVH,求解角度。 在上述算法中并没有考虑噪声,文献[12]指出加入噪声后,最终投影到集合R,H中的T(u)仍然是Toeplitz矩阵,能够完成对半正定矩阵S的构造,能够实现DOA估计。 文献[12]认为,因为矩阵T(u)和矩阵Z是矩阵S的子矩阵,所以不需要将T(u)和Z投影到集合E中,只需要将S投影到集合E即可,求解出S后即可得到T(u),再对T(u)进行范德蒙分解,进而求解角度。本文对APG算法进行改进,通过矩阵在集合H,P和M之间的交替迭代投影来解决式(5)中的半定规划问题,直接求解T(u)而不是S,将问题的维数减少,降低所求矩阵维度,进而降低计算量。 在不考虑噪声的情况下,将式(1)、式(14)代入式(5)可得: (16) 由式(16)可得,A,Y,T(u)具有相同的列空间。由范德蒙分解的唯一性可知,任何具有与A相同列空间的Toeplitz矩阵都可以分解为A和一个对角矩阵D的组合。因此T(u)的最优解属于集合M并且与测量值Y的信号子空间有相同的列空间。可以通过T(u)可以在集合H,P,M中交替迭代投影得到,不需要再求解半正定矩阵S,进而降低所求矩阵的维度,减少了计算量。算法具体步骤如下: 步骤1 已知雷达观测值Y∈CM×L,目标个数K个,判定收敛的界限ε。设定随机初始值T0(u)∈CM×M。 步骤2 根据测量值的协方差矩阵求出信号子空间ES: 其中,ΛS和ES为前K个大的特征值和对应的特征向量;ΛN和EN剩余M-K个特征值和对应的特征向量。 步骤3 将T(u)在集合M,P,H中依次迭代投影: 步骤5 对所求得的T(u)进行范德蒙分解T(u)=VDVH,求解角度。 在仿真实验中,设置雷达为阵元数为M的均匀线阵,阵元间距为发射信号波长的0.5倍,空域中目标个数为K=3,判定收敛的界限ε=0.001。进行200次蒙特卡罗仿真,通过实验将本文算法与APG算法的标准差、均方根误差和时间进行了比较。 实验中将三个目标估计值的标准差累加比较,定义为: (17) 定义均方根误差(RMSE)为: (18) 图1为两种算法在快拍数为L=30,阵元数为M=20,不同SNR条件下标准差、均方根误差和时间的比较。 由图1可知,随着信噪比的增大,两种算法的标准差和均方根误差都逐渐减小,算法精度逐步提高;所用时间逐渐减少,计算量减少。在相同信噪比条件下,本文算法的标准差和均方根误差与APG算法相近,估计精度相近,但本文算法的所用时间明显小于APG算法,实时性更好,性能更优。 图1 不同信噪比时两种算法的均标准差、方根误差和时间Fig.1 Mean standard deviation, square root error and time of the two algorithms under different SNR 图2为两种算法在信噪比为30 dB,阵元数为M=20,不同快拍数条件下标准差、均方根误差和所用时间的比较。由图可知,随着快拍数的增多,两种算法的标准差和均方根误差都逐渐减小,算法精度逐步提高;所用时间逐渐增多,计算量增大。在相同快拍数条件下,本文算法的标准差和均方根误差与APG算法相近,估计精度相近,但本文算法比APG算法的所用时间更少,实时性更好,性能更优。 图2 不同快拍数时两种算法的标准差、均方根误差和时间Fig.2 Standard deviation, root mean square error and time of the two algorithms under different snapshots 图3为两种算法在信噪比为30 dB,快拍数为L=30,不同阵元数条件下标准差、均方根误差和所用时间的比较。由图可知,随着阵元数的增多,两种算法的标准差和均方根误差都逐渐减小,算法精度逐步提高;所用时间逐渐增多,计算量增大。在相同阵元数的条件下,本文算法的标准差和均方根误差与APG算法相近,估计精度相近,但本文算法所用的时间明显小于APG算法,实时性更好,性能更优。 图3 不同阵元数时两种算法的标准差、均方根误差和时间Fig.3 Standard deviation, root-mean-square error and time of the two algorithms under different array Numbers 本文提出了基于交错投影的无网格降维DOA估计算法。该算法在求解无网格DOA估计的半定规划问题时,不再求解半正定矩阵S,而是直接求解Toeplitz矩阵T(u),降低所求矩阵的维度,减少了计算量。仿真结果表明,该算法与APG算法相比,在相同信噪比,快拍数或阵元数的条件下能够保证估计精度,同时减少了计算时间,具有更好的实时性,性能更优。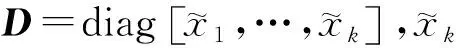
1.3 APG算法

Z,S∈P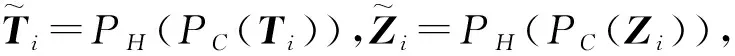
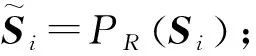
2 降维处理的APG算法
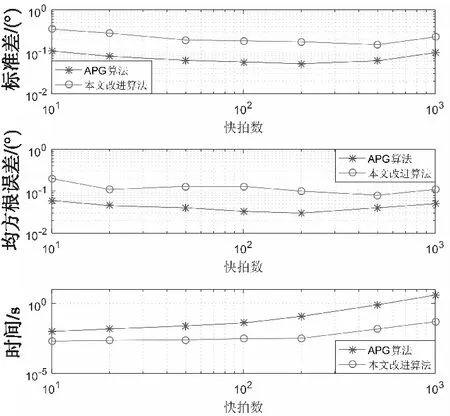
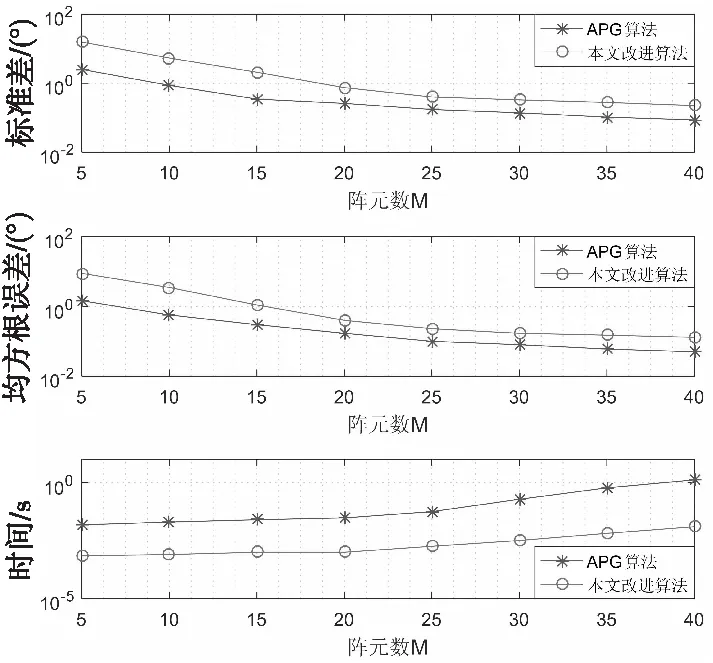
3 仿真验证
4 结论

