基于Adams的供输弹机构运动仿真分析

张勃寅 马 俊

（1.陕西华通机电制造有限公司,陕西 西安 710062；2.陕西普利美材料科技有限公司,陕西 西安 710065)

传统的弹丸发射系统多采用火药作为弹丸的发射动能[2]，但是在某些特殊环境和空间要求下，则需要采用压缩气体代替传统火药燃烧产生的高压气体来完成对弹丸的发射[3]。另外，现有利用压缩轻质气体驱动弹丸发射的装置中，由于需要确保弹丸在发射过程中处于相对密闭的空间，多用于实验室内的高速弹丸运动的毁伤效应试验研究[4]。

根据某些特殊环境和空间要求，本文设计了一款新型动能发射装置，如图1所示。该装置采用轻质压缩气体瞬间释放来产生高压气源，来实现弹丸的动能发射。结合新型弹丸的要求，该款动能发射装置设计了新型的供输弹机构[5]。为了研究该新型供输弹机构的动力学特性，本文利用Inventor软件对其进行了三维建模，采用Adams动力学仿真软件对供输弹机构的关键动力学参数进行了仿真分析[6]，并得到影响弹丸输送性能的因素，进而对其动力学参数进行优化设计。

图1 新型动能发射装置

1 供输弹机构工作原理

为了满足装弹数量、供弹速度以及结构轻量化的要求，该新型供输弹机构的左、右双弹鼓水平对称地安装于供弹段两侧，左、右弹鼓通过供弹球体交替切换供弹。单个弹鼓中弹丸为单圈排列，可满足一定的有效载弹量要求。供输弹机构的三维模型如图2所示。

图2 供输弹机构三维模型

供输弹机构的工作过程如下：首先，在棘轮机构控制下涡卷弹簧将势能传递给推弹杆，从而使推弹杆做手表指针式运动，并将弹丸依次推至弹鼓出弹口；其次，在电机驱动下，供弹段内的供弹球体旋转90°，供弹球体入弹口与弹鼓出弹口对接，在推弹杆的作用下，弹丸被推入供弹球体；最后，供弹球体回转90°，完成供弹动作。

2 初始条件设计

为了保证模型在仿真分析时的精度和效率，考虑到供输弹机构的复杂性，将涡卷弹簧作用力简化为作用到推弹杆中心的恒定转矩，提取弹鼓蜗壳的内表面，将其简化为壳单元模型，去掉供弹球体的外壳、轴承以及棘轮等与分析无关的零件，如图3所示。

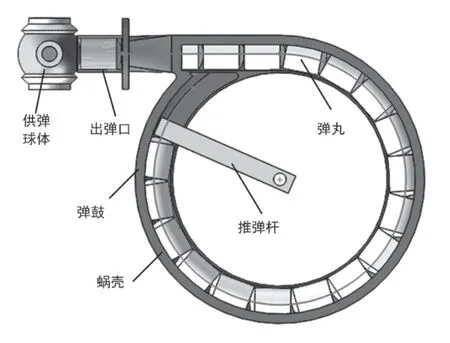
图3 供输弹机构三维简化模型

另外，弹鼓蜗壳、供弹球体、推弹杆为铝合金材料，弹丸为聚碳酸酯材料，其力学属性如表1所示。各零件接触部位的摩擦系数如表2所示。

表1 简化模型材料及力学属性

表2 各运动件的摩擦系数

根据供输弹需求以及机构尺寸，弹丸质量为18 g，其排列分布半径为100 mm，涡卷弹簧转矩为2 N·m，供弹球体转动速度为45°/s（即0.125 r/s），通过改变旋转的启动加速度和停止减速度，对弹丸的供弹、输弹过程的速度、加速度等动力学特性进行分析与优化。

3 不同条件下的仿真结果及分析优化

在机械动力学仿真软件Adams中对转动机构模型进行参数化时，必须确定模型参数化的方式以及变量。在Adams软件中包含4种控制方式，本文选用设计变量的方法对整个机构的变量进行参数化[7]。

由于该供输弹机构是由外部联结的直流电机提供驱动源，由直流电机来控制供弹球体的转动状态，同时涡卷弹簧的输出力矩是在弹丸安装时进行调整，弹丸弹出供弹球体的速度由整个发射系统的发射作用力所决定。因此，将供弹球体启动和停止的加速度、涡卷弹簧输出转矩、弹丸弹出供弹球体的速度等参数设为参数变量，并转化成相应的驱动函数，对整个运动机构进行仿真计算分析。

3.1 条件一：供弹球体以1800°/S2的加速度启动和停止

3.1.1 条件一的参数设计

当供弹球体以加速度为1800°/S2（即5r/S2）进行启动和停止时，为了保证90°的旋转角度和45°/s的最大转速，设计了供弹球体转速随时间变化的规律，如图4所示。

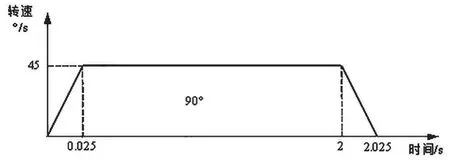
图4 供弹球体转速随时间变化的规律

按照Adams软件操作规范，结合供弹球体转速随时间变化的规律曲线，为涡卷弹簧转矩、供弹球体转速和弹丸弹出供弹球体速度等参数设置了随时间变化的驱动函数。

涡卷弹簧转矩：STEP(time,0,0,0.05,2000)；

供弹球体转速：STEP (time,0,0d,0.05,0d)+STEP (time,0.1,0d,0.125,-45d)+STEP (time,2.1,-45d,2.125,0d) +STEP (time,2.3,0d,2.325,45d)+STEP (time,4.3,45d,4.325,0d)+STEP (time,4.5,0d,4.525,-45d)+STEP (time,6.5,-45d,6.525,0d)+STEP (time,6.7,0d,6.725,45d)+STEP (time,8.7,45d,8.725,0d)；

弹丸弹出供弹球体速度：STEP(time,4.325,0,4.4,-10)，STEP(time,8.725,0,8.8,-10)。

3.1.2 条件一的仿真分析结果

（1）供弹球体转动规律如图5所示。0 s～0.1 s位于0°位置，供弹球体保持静止状态；0.1 s～0.125 s，供弹球体以1800°/S2的加速度顺时针加速至45°/s；0.125 s～2.1 s，供弹球体以45°/s的速度顺时针旋转；2.1 s～2.125 s，供弹球体以1800°/S2的加速度减速至0°/s，此时供弹球体已经顺时针转过90°，旋转到取弹状态；2.125 s～2.3 s，供弹球体保持取弹状态，等待弹丸进入供弹球体；2.3 s～2.325 s，供弹球体以1800°/S2的加速度逆时针加速至45°/s；2.325 s～4.3 s，供弹球体以45°/s的速度逆时针旋转；4.3 s～4.325 s，供弹球体以1800°/S2的加速度减速至0°/s，此过程供弹球体逆时针转过90°，第一发弹丸在发射力作用下从发射身管中射出。第二发弹丸以此往复。

图5 供弹球体角速度变化规律

（2）弹丸1的加速度变化曲线如图6所示。在初期，弹丸在推弹杆的转矩作用下产生加速度，推动弹丸依次进入弹鼓出弹口和供弹球体，而后在发射力作用下加速射出。

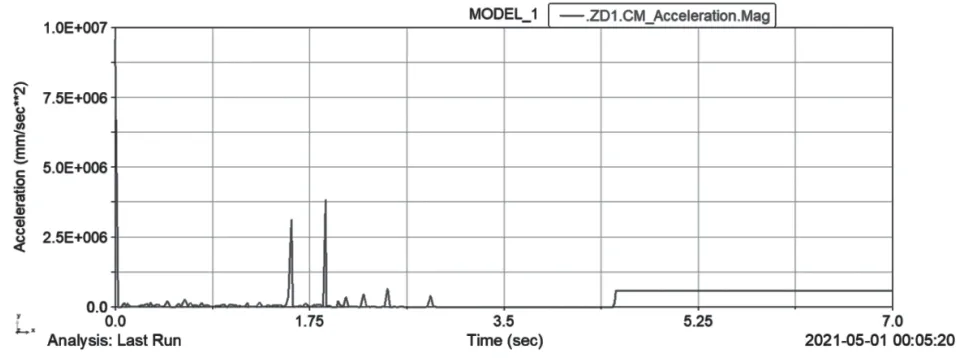
图6 弹丸1加速度变化规律

（3）弹丸2的加速度变化曲线如图7所示。推弹杆的转矩通过弹丸2作用在弹丸1上，使弹丸产生加速度，而当弹丸1在2.3 s左右将要进入供弹球体的时候，弹丸2的加速度会产生突变，待弹丸1完全进入供弹球体后，加速度又恢复至很小，直到6.5 s左右，弹丸2进入供弹球体，待供弹球体逆时针转过90°后，在发射力作用下弹丸2加速发射。

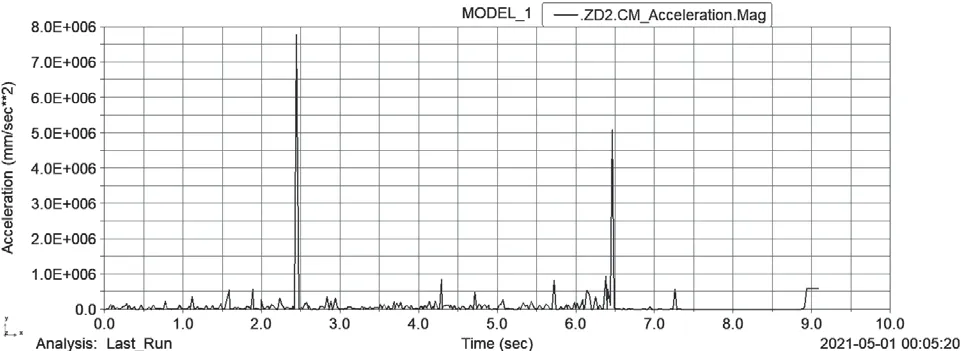
图7 弹丸2加速度变化规律

（4）供输弹过程中，弹丸1、弹丸2的速度变化曲线如图8所示。在推弹杆的作用下，0 s～1.7 s，弹丸一起运动进入出弹口，并压紧供弹球体，等待供弹；2.1 s～2.2 s，弹丸一起运动，进入供弹球体，等待输弹；4.3 s后，弹丸1倍加速射出；弹丸2进入第二个供输弹循环，与弹丸1相同。

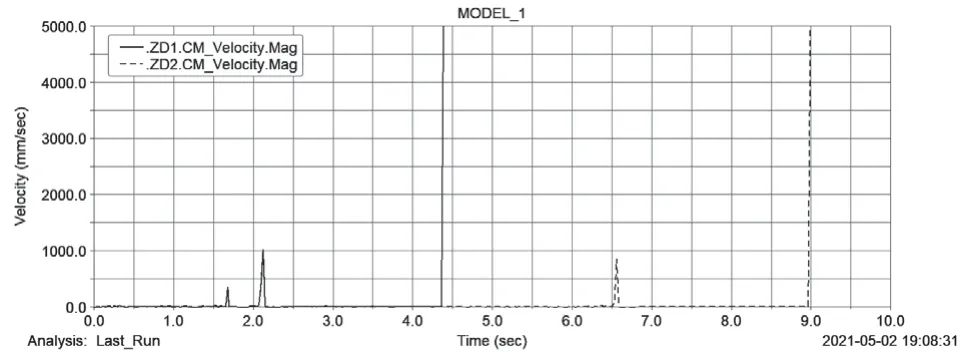
图8 弹丸1、弹丸2的速度变化规律

（5）供弹球体的角加速度如图9所示。在0.1 s～0.125 s，供弹球体由静止到被赋予顺时针加速度，所以加速度发生了突变；0.125 s～2.1 s，供弹球体顺时针匀速转动，加速度为零；2.1 s～2.125 s，供弹球体由匀速运动到被赋予顺时针减速的加速度，供弹球体加速度发生突变；此时，供弹球体已经顺时针转过90°，进入静止状态，等待弹丸进入；2.3 s～2.325 s，供弹球体由静止状态被赋予逆时针加速度，供弹球体加速度产生突变；2.325 s～4.3 s，供弹球体逆时针匀速转动，加速度为零；4.3 s～4.325 s，供弹球体被赋予逆时针减速的加速度，供弹球体的加速度再次发生突变，至此，弹丸1被发射出去；4.5 s～8.725 s是弹丸2被发射出去的过程，与弹丸1相同。

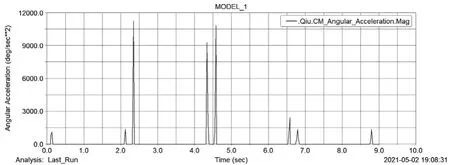
图9 供弹球体角加速度变化规律

（6）供弹球体所受到的转矩如图10所示。在供输弹过程中，由于弹丸的摩擦和碰撞，供弹球体所受到的转矩会出现波动。在供弹球体的转动过程中，转矩峰值出现在供弹球体转至进弹口和弹丸接触时，是由弹丸与供弹球体发生碰撞造成的，但是最大转矩不足80 N·mm，满足1 N·m以内的设计要求。

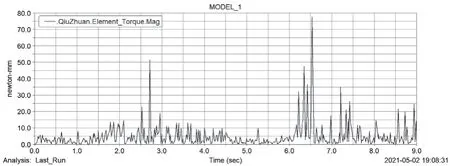
图10 供弹球体转矩变化规律

3.2 条件二：供弹球体以900°/S2的加速度启动和停止、涡卷弹簧转矩输出降低6%

考虑到供弹球体启动加速度过高的稳定性，以及涡卷弹簧输出转矩随弹丸供弹运动逐渐衰减，将供弹球体加速度大小设置为900°/S2（即2.5r/s2），并且将弹丸供弹过程中涡卷弹簧的输出转矩从2 N·m降低6%，对供弹运动进行重新仿真分析。

3.2.1 条件二的参数设计

与条件一类似，为涡卷弹簧转矩、供弹球体转速和弹丸弹出供弹球体速度等参数设置了随时间变化的驱动函数。

涡卷弹簧转矩：STEP(time,0,0,0.05,2000)+STEP(ti me,0.1,2000,8.825,1880)；

供弹球体转速：STEP(time,0,0d,0.05,0d)+STEP(time,0.1,0d,0.15,-45d)+STEP(time,2.1,-45d,2.15,0d)+STEP(time,2.325,0d,2.375,45d)+STEP(time,4.325,45d,4.375,0d)+STEP(time,4.55,0d,4.6,-45d)+STEP(time,6.55,-45d,6.6,0d)+STEP(time,6.775,0d,6.825,45d)+STEP(time,8.775,45d,8.825,0d)；

弹丸弹出供弹球体速度：STEP(time,4.375,0,4.45,-10)，STEP(time,8.825,0,8.9,-10)。

3.2.2 条件二的仿真分析结果

（1）弹丸1的加速度变化规律如图11所示。弹丸在进入供弹球体之前的加速度很小，当供弹球体旋转90°，在推弹杆转矩的推动作用下，弹丸1进入供弹球体时加速度出现突变。

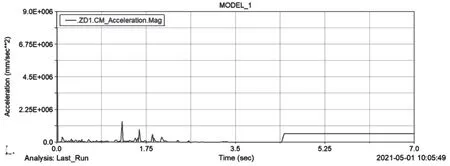
图11 弹丸1的加速度变化规律

（2）弹丸2的加速度变化规律如图12所示。弹丸2的加速度波动比弹丸1明显增大，但是加速度峰值小于弹丸1；另外，与涡卷弹簧转矩变化不同，弹丸2的加速度没有减小的情形，加速度峰值变化不大，且变化规律也相似。

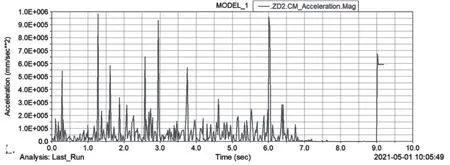
图12 弹丸2的加速度变化规律

（3）供弹球体的角加速度变化曲线如图13所示。由于涡卷弹簧转矩逐渐减小，弹丸和供弹球体之间的作用力也会减小，从而使得供弹球体的加速度大于条件一相应位置的加速度。

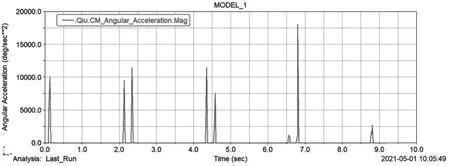
图13 供弹球体的角速度变化规律

（4）供弹球体转矩变化规律如图14所示。与条件一情况类似，由于弹丸的摩擦和碰撞，供弹球体所受到的转矩会出现波动，最大转矩180 N·mm比条件一的最大转矩要大，但满足1 N·m以内的设计要求。

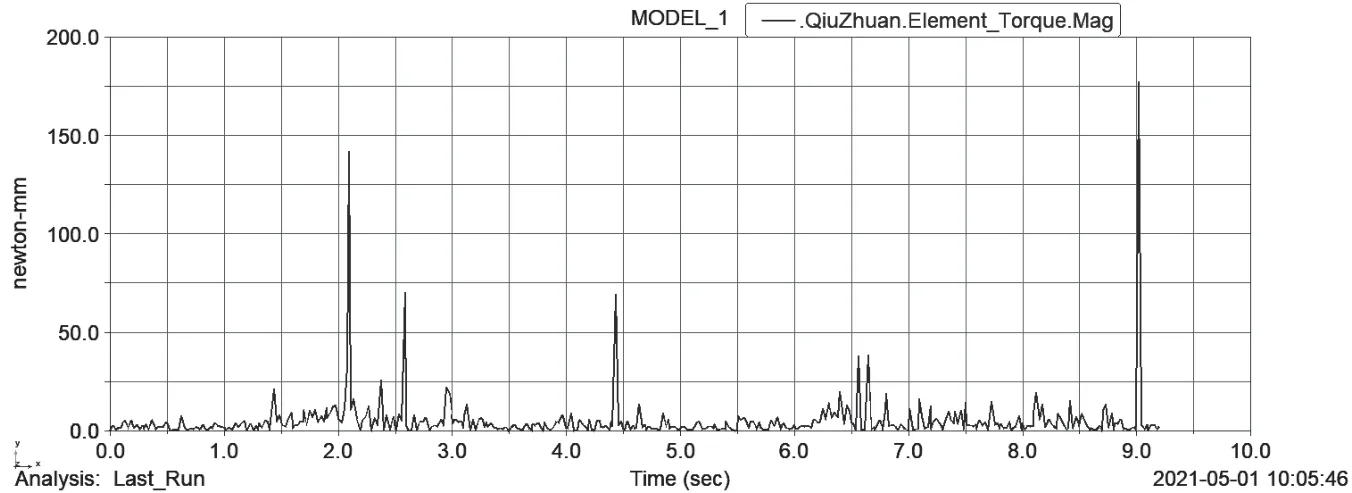
图14 供弹球体转矩变化规律

4 结语

在条件一和条件二下，供弹球体的角加速度输入参数不同，仿真结果显示弹丸1和弹丸2的加速度以及供弹球体的角加速度变化规律也不同。由此可以发现，当供弹球体的角加速度由1800°/S2变为900°/S2时，弹丸在进入供弹球体过程中加速度的变化更加趋于平缓；另外，从仿真结果也可以看出，这一改变也使得供弹球体的角加速度的最大值有明显的下降，但是供弹球体所受转矩的最大值变化不明显。同时，当涡卷弹簧转矩减小，弹丸和供弹球体之间的作用力减小，从而供弹球体受到的阻力转矩减小，所以供弹球体的转矩会增加，但是变化趋势基本不变。

供输弹机构是某新型发射装置的关重部件，其设计和制造的质量，将直接影响整个装置功能的实现。通过利用Adams参数优化设计功能对供输弹机构进行仿真分析，不仅避免了复杂数学模型的建立和推导，还能准确得到供输弹过程的运动规律，结构实际应用时对电机、涡卷弹簧等驱动部件的输出能力，通过不同条件和参数的对比分析，得到优化的参数组合，缩短研制周期，对优化改进其他机构具有一定的参考意义。