最大度为6且不含5-圈和相邻4-圈的平面图是7-全可染的*

张静雯

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

本文所研究的图是有限简单无向图，文中未加定义的术语和记号参阅文献［1］．

如果图G可嵌入到平面上，使得边仅在端点处相交，则称图G是可平面图;可平面图在平面内的一个嵌入叫平面图．对于平面图G，分别用V，E，F，Δ和δ表示平面图G的顶点集、边集、面集、最大度和最小度．k-圈是指长度为k的圈;两个圈相邻是指该两个圈至少有1条公共边．

设平面图G=(V，E)，若映射 φ:V∪E→{1，2，…，k}，使得对任意相邻或相关联的元素 x，y∈V∪E都有φ(x)≠φ(y)，则称G是k-全可染的．显然，给每一个图进行全染色至少要用Δ+1种颜色．文献［2-3］猜想:任何简单图G都是(Δ+2)-全可染的．这一猜想就是著名的全染色猜想(Total Coloring Conjecture)，简记为 TCC．

即使对于平面图，TCC也未得到完整的证明．唯一未解决的困难情形是Δ=6．这方面的一些研究结果可参见文献［4-8］．人们期望得到关于简单平面图全染色的最好结果，即证明平面图是(Δ+1)-全可染的．到目前为止，已经证明了在大多数情况下，简单平面图是(Δ+1)-全可染的．文献［9-11］分别证明了Δ≥11，Δ=10和Δ=9的平面图是(Δ+1)-全可染的;文献［12］证明了Δ≥7且不含4-圈的简单平面图是(Δ+1)-全可染的．本文研究的是关于Δ=6的平面图的全染色问题，得到如下结果:

定理1 设G是Δ=6且不含5-圈和相邻4-圈的平面图，则图G是7-全可染的．

1 定理1的证明

假设定理1不成立，并设图G是定理1的一个使σ(G)=|V|+|E|最小的反例，即Δ(G)=6且不含5-圈和相邻4-圈，它本身不是7-全可染的，但它的每一个真子图都是7-全可染的，则图G有以下几个性质:

断言1［9］图G是2-连通的．

δ≥2，且因为图G是2-连通的，所以G的每个面的边界都是圈．

把度数为k的点叫做k-点;类似地，把度数至少为k的点叫做k+-点;把度数至多为k的点叫做k--点．(i，j)-边是指此边的2个端点的度数分别为 i和 j;(i，j，k)-面是指此 3-面上的点的度数分别为 i，j，k．

断言 2［13］设 xy∈E．若 d(x)≤3，则d(x)+d(y)≥Δ +2=8．

特别地，G中2-点只与6-点相邻，3-点只与5+-点相邻．

断言3［13］图G中所有(2，6)-边的导出子图是一个森林．

断言4 G不含图1所示的结构．其中标记为·的点在G中没有其他邻点．

证明 假设G有如图1(a)所示的子结构．由G的极小性可知，G'=G-u1u3是7-全可染的．假设φ是G'的一个7-全染色，抹去u1和u4的色，则得到图G的一个部分全染色，其中未染的元素是u1u3，u1和u4．易见，当u1u3染好后，u1和u4的色可重染好．所以，以下只需看u1u3是否可染好．S(u)表示在φ

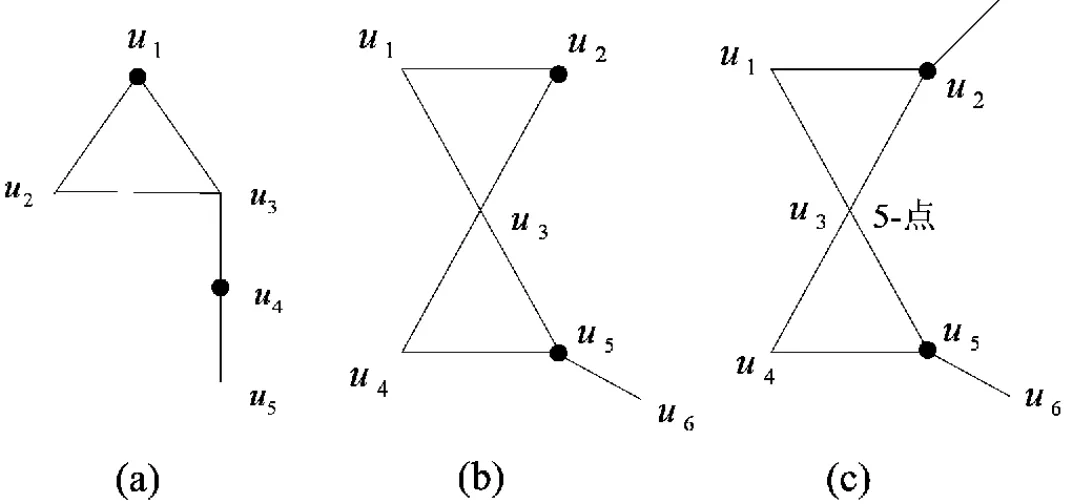
图1 可约构型

若7∈{φ(u4u5)，φ(u5u6)}，则当 φ(u4u5)=7时，如果 φ(u5u6)≠φ(u3u4)，那么交换 u3u4与 u4u5的色，再将φ(u3u4)染给u2u3;如果φ(u5u6)=φ(u3u4)，那么交换u1u2与u1u3的色，再将φ(u1u3)染给u3u5，φ(u3u5)染给 u2u3;当 φ(u5u6)=7 时，则交换 u1u2与 u1u3的色，如果 φ(u4u5)≠φ(u1u3)，那么再将 φ(u1u3)染给 u3u5，φ(u3u5)染给 u2u3;如果 φ(u4u5)=φ(u1u3)，那么交换 u3u4与 u4u5的色，再将φ(u3u4)染给u2u3;最后，重染u2和u5，又得G是7-全可染的，矛盾．

假设G有如图1(c)所示的子结构．由G的极小性可知，G'=G-u2u3是7-全可染的．假设φ是G'的一个7-全染色，抹去u2和u5的色，则得到图G的一个部分全染色，其中未染的元素是u2u3，u2和u5．

若|S(u2)∪S(u3)|≤6，则u2u3可染;再重染u2和u5，则G是7-全可染的，矛盾．

若|S(u2)∪S(u3)|=7，不妨设S(u3)={1，2，…，5}，S(u2)={6，7}，则可断言{φ(u4u5)，φ(u5u6)}={6，7}．否则，若 6∉{φ(u4u5)，φ(u5u6)}，则可将 φ(u3u5)染为 6，φ(u3u5)染给 u2u3;同理可证，7∈{φ(u4u5)，φ(u5u6)}．此时交换u3u4与u4u5的色，再将 φ(u3u4)染给 u2u3;最后，重染 u2和 u5，又得 G是7-全可染的，矛盾．断言4证毕．

2 权转移

以下将运用Discharging方法导出矛盾，完成定理1的证明．首先，给图G的每个顶点v分配初始权

以下将定义一个权转移规则，重新分配点和面的权，设ch'(x)是重新分配点和面的权后元素x∈只是在同一个图的点和面之间进行权转移，则权的总和应保持不变，所以得出 -12≥0的矛盾，完成定理1的证明．

权转移规则如图2所示．

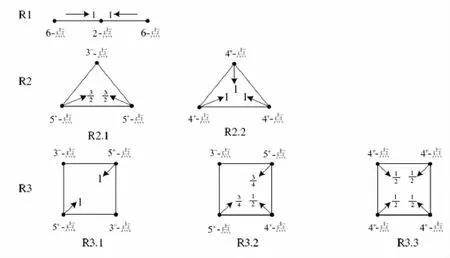
图2 权转移规则

R1:转向2-点的权

与2-点相邻的2个6-点都向2-点转移权1．

R2:转向3-面的权

R2．1:若3-面与3--点相关联，则3-面上的2个5+-点都向3-面转移

R2．2:若3-面不与3--点相关联，则3-面上的3个4+-点都向3-面转移权1．

R3:转向4-面的权

R3．1:若4-面与2个3--点相关联，则4-面上的2个5+-点都向4-面转移权1;

R3．2:若4-面与1个3--点相关联，则与3--点相邻的2个5+-点都向4-面转移的4+-点向4-面转

R3．3:若4-面不与3--点相关联，则4-面上的4个4+-点都向4-面转

首先考察面的新权．

设 f为 3-面．若 f与 3--点相关联，则根据 R则根据 R2．2，ch'(f)≥ch(f)+1 ×3=0．

设 f为4-面．若 f与2 个3--点相关联，则根据 R3．1，ch'(f)≥ch(f)+1 ×2=0;若 f与1 个3--点相

由图G不含5-圈知图G不含5-面，故无需验证5-面的新权．

设f为6+-面．由权转移规则知f既不转出权也不接受权，因此ch'(f)=ch(f)=d(f)-6≥0．

综上所述，对任意的面f∈F，ch'(f)≥0．

其次考察顶点的新权．

设v为2-点．由断言2和R1知，ch'(v)=ch(v)+1×2=-2+2=0．

设v为3-点．由权转移规则知v既不转出权也不接受权，即ch'(v)=ch(v)=0．

下面用t表示与v相关联的3-面的个数．

的4-面，转移权1给与它相邻的2-点．

用n表示与v相邻的2-点个数，显然，n≤6．与6-点相邻的2-点分布情况如图3所示．以下分2种情形讨论:

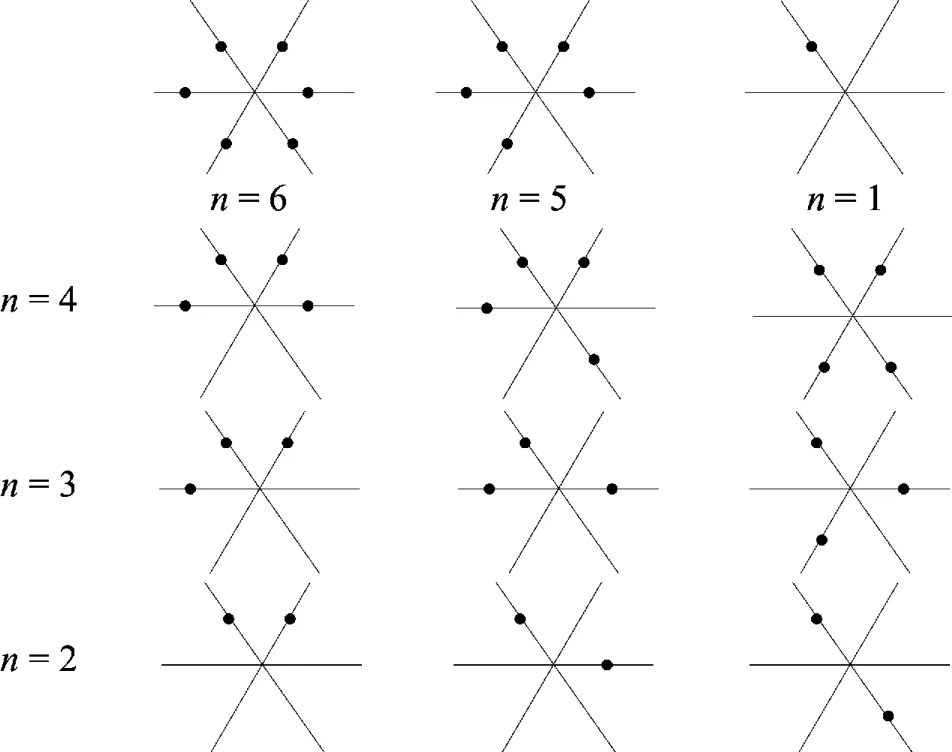
图3 与6-点相邻的2-点分布情况(1≤n≤6)

最复杂的为t=0．用m表示与v相关联的4-面个数，由图G不含5-圈和相邻4-圈知m≤3．

注2 由断言3和图G不含5-圈知，与v关联且关联的2个与v相邻的2-点的面是6+-面．

n=6．由注1和注2知，ch'(v)≥ch(v)-1×6=0．

n=5．由注2和图 G不含相邻4-圈知 v至少关联5个6+-面，且 m≤1，从而根据注1，ch'(v)≥ch(v)-1×5-1=0．

n=4．由注2和图G不含相邻4-圈知m≤2，从而根据注1，ch'(v)≥ch(v)-1×4-1×2=0．

n=3．由注2和图G不含相邻4-圈知m≤3，从而根据注1，ch'(v)≥ch(v)-1×3-1×3=0．

n=2．由注2和图G不含相邻4-圈知m≤3，从而根据注1，ch'(v)≥ch(v)-1×2-1×3≥0．

n=1．由图G不含相邻4-圈知m≤3，从而根据注1，ch'(v)≥ch(v)-1-1×3≥0．

至此，对任意的x∈V∪F，ch'(x)≥0已得到验证．定理1得证．

［1］Bondy J A，Murty U S R．Graph theory with applications［M］．London:Macmillan Press，1976．

［2］Vizing V G．Some unsolved problems in graph theory［J］．Uspekhi Mat Nauk，1968，23(6):117-134．

［3］Behzad M．Graphs and their chromatic numbers［D］．East Lansing:Michigan State University，1965．

［4］Kostochka A V．The total coloring of a multigraph with maximal degree 4［J］．Discrete Math，1977，17(2):161-163．

［5］Kostochka A V．The total chromatic number of any multigraph with maximal degree five is at most seven［J］．Discrete Math，1996，162(1/2/3):199-214．

［6］Rosenfeld M．On the total coloring of certain graphs［J］．Israel J Math，1971，9(3):396-402．

［7］Vijayaditya N．On total chromatic number of a graph［J］．London Math Soc，1971，3(2):405-408．

［8］Yap H P．Total coloring of graphs［M］．Belin:Spring-Verlag，1996．

［9］Borodin O V，Kostochka A V，Woodall D R．Total coloring of planar graphs with large maximum degree［J］．Graph Theory，1997，26(1):53-59．

［10］Wang Weifan．Total chromatic number of planar graphs with maximum degree ten［J］．Graph Theory，2007，54(1):91-102．

［11］Kowalik L，Sereni J S，Škrekovski R．Total coloring of plane graphs with maximum degree nine［J］．SIAM Discrete Math，2008，22(4):1462-1479．

［12］Hou Jianfeng，Liu Guizhen，Cai Jiansheng．List edge and list total coloring of planar graphs without 4-cycles［J］．Theoret Comput Sci，2006，369:250-255．

［13］Borodin O V．On the total coloring of planar graphs［J］．Reine Angew Math，1989，394(1):180-185．