一类4维Lotka-Volterra系统的Hamilton结构及动力学*

赵晓华, 戴灿华

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

一类4维Lotka-Volterra系统的Hamilton结构及动力学*

赵晓华, 戴灿华

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

运用动力系统的方法研究了一类具有Hamilton结构的4维保守型Lotka-Volterra系统.结果显示:这类系统具有很复杂的动力学性质,相空间包含至少3族周期轨道;对一般参数,这个系统是不可积的,会出现Hamilton混沌.

Lotka-Volterra系统;Hamilton结构;周期解;Lyapunov指数;Hamilton混沌

0 引 言

本文涉及的Lotka-Volterra系统是指下面的常微分方程组:

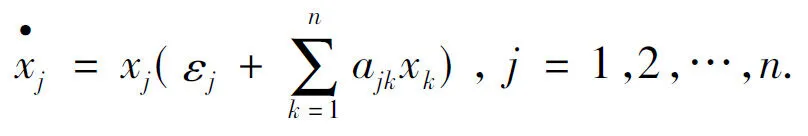
式(1)中:xj表示第j个物种的种群密度;A=(ajk)称为作用矩阵,表示物种间的相互作用关系;εj是与环境相关的参数.

自19世纪20年代Lotka和Volterra分别在研究化学反应和生物问题时提出上述Lotka-Volterra(LV)系统以来,方程组(1)已经被广泛应用于物理、化学、生物、动态博弈论、经济和其他的社会科学中,成为应用数学领域中一个重要的微分方程模型,还被应用于许多热门学科,如神经网络、生物反应、细胞演化和病毒传播等[1-6],LV系统受到数学及其他学科领域的关注越来越多.在过去的80多年里,对LV系统的理论及应用研究成果大量涌现[7-8].

但是,除了2维的Lotka-Volterra系统的动力学性质和一些特殊类型的高维Lotka-Volterra系统已分析清楚外,一般的高维Lotka-Volterra系统的动力学性质还远远没有弄清楚,有待深入研究.

研究表明,Lotka-Volterra系统的动力学性质和它的作用矩阵的代数性质有着密切的关系.根据作用矩阵A的不同性质,Lotka-Volterra系统可分为3类[5](定义1).

定义1具有作用矩阵A=(aij)的Lotka-Volterra系统称为:

1)合作型(或竞争型),如果对任意i≠j,aij≥0(aij≤0);

2)保守型,如果存在一个正对角矩阵D>0,使得AD是反对称的;

3)耗散型,如果存在一个正对角矩阵D>0,使得在二次型意义下AD≤0.

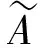
以往的研究主要涉及合作(或竞争)型LV系统,对保守型和耗散型系统的研究相对较少[5-7].其中特别值得注意的是1998年Duarte等在文献[5]中对这两类系统的研究,他们证明:保守型LV系统若存在正平衡点,则它具有广义Hamilton结构,可以表示为Poisson流形上的广义Hamilton系统;而具有正平衡点的稳定耗散LV系统存在一个整体吸引集,其上的动力学控制方程是一个较低维数的具有广义Hamilton结构的保守型LV系统.关于Hamilton和广义Hamilton系统的相关知识可参阅文献[9-10].

根据Duarte等的这些结论可以得出,若这个吸引集是单点集,则原LV系统是全局渐进稳定的;若吸引集不是单点集,则需进一步研究吸引集上的子系统的轨道性质.因此,为了弄清稳定耗散系统在吸引集上的动力学性质,本质上就是要研究具有广义Hamilton结构的保守型LV系统的动力学性质.

本文研究了一类具有广义Hamilton结构的4维保守型LV系统,这个系统包含至少3族周期轨道,而对一般的参数是不可积的,并且会出现Hamilton混沌.进而也表明: 一般而言,稳定耗散LV系统吸引集的结构可能非常丰富而复杂,值得深入系统地研究.

1 Hamilton结构及平衡点稳定性分析

本文考虑如下的4维Lotka-Volterra系统:

对应的作用矩阵为

式(3)中:已被标出的元素aij≠0;aijaji<0.考虑到系统(2)的特殊结构及实际应用背景,只对不变区域R4+={x=(x1,x2,x3,x4)∈R4|xj>0,j=1,2,3,4}上的轨道性质进行研究.

在假设条件aijaji<0下,系统(2)实际上是一个保守型系统,因为可取对角矩阵D=diag(d1,d2,d3,d4)的对角元素为

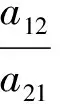
则可使DA为反对称矩阵.进一步,容易验证变换xj→djxj保持系统(2)的形式不变,但作用矩阵变为DA,为反对称矩阵.

因此,不失一般性,直接假定系统(2)的作用矩阵(3)满足以下条件:

容易验证,若参数bj(j=1,2,3,4)满足条件

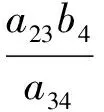
则系统(2)存在唯一正平衡点

另一方面,在光滑函数空间C∞(R4+)上定义Poisson括号{·,·}为

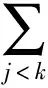
式(8)中,A=(ajk)是满足条件式(5)的系统(2)的作用矩阵.根据辛流形及其上定义的Hamilton系统的理论[9],直接验证可知{R4+,{·,·}}构成一个4维辛流形,并且有命题1成立.

命题1在假设式(5)和式(6)成立的情况下,LV系统(2)是4维辛流形{R4+,{·,·}}上的Hamilton系统,可将系统(2)改写为如下Hamilton形式:

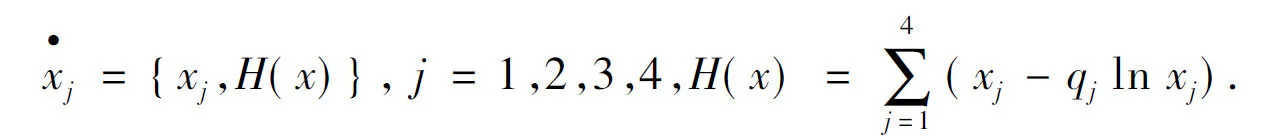
命题2在假设式(5)和式(6)成立的条件下,LV系统(2)的正平衡点q是Lyapunov稳定的.

最后,利用Morse引理[11]得:对任意h>0,水平集Mh={x∈R4+|H(x)-H(q)=h}拓扑等价于一个3维球面S3.

2 周期轨道

为进一步研究系统(2)的周期解,先介绍下面的Lyapunov中心定理[10].

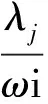
对于系统(2)的唯一正平衡点q,简单计算即可得到其相应的特征方程为

式(10)中:

由式(5)和式(6)知P>0,Q>0,Δ=P2-4Q>0.于是可得命题3.

命题3在式(5)和式(6)成立的条件下,系统(2)在正平衡点q处的特征方程(10)有2对简单共轭纯虚根,分别为:

i.

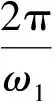
系统(2)除了以上周期解外,还可能存在其他周期解.

容易验证,若系统(2)中的a23=0,但式(5)和式(6)中的其他式子仍满足,则系统变为2个独立的2维LV系统:

此时系统是可积的,并有2个独立的首次积分:

而且在平衡点q处的特征值为2对简单纯虚根:

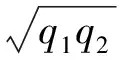
因此,系统(12)的轨道由2个子系统的轨道(均为周期轨道)组合而成,分布于I1(x)和I2(x)确定的水平集上,这个水平集由轨道的初值确定,拓扑等价于2维环面S1×S1,仅当2个子系统解的周期之比为有理数时,对应的4维系统(12)的解才是周期解,否则为拟周期环面解.

特别地,若(φ1(t,I1),φ2(t,I1))和(φ3(t,I2),φ4(t,I2))分别是2个子系统的周期解,则(φ1(t,I1),φ2(t,I1),q3,q4)和(q1,q2,φ1(t,I2),φ2(t,,I2))就是对应4维系统(12)的2个周期解,而且易证它们都是Hamilton系统(2)在参数a23=0时的椭圆型周期解.根据Hamilton系统的性质,当a23≠0充分小时,Hamilton系统(2)仍然存在2个与它们对应的周期解.

定理2在式(5)和式(6)成立的条件下,当a23≠0充分小时,系统(2)存在2族分别对应于(φ1(t,,I1),φ2(t,I1),q3,q4)和(q1,q2,φ1(t,I2),φ2(t,,I2))的周期解.

3 不可积性与Hamilton混沌

根据Hamilton系统中的Liouville完全可积性定义[9-10],若4维系统(2)还存在一个独立于Hamilton函数H(x)的首次积分I(x),则它的解均在H(x)和I(x)确定的水平集上,而这个水平集是紧致的(H(x)的水平集拓扑等价于3维球面).故由完全可积性定理知,该水平集拓扑等价于2维不变环面,其上若存在周期解,则必属于定理1中那两族之一.

另一方面,对充分小的a23≠0,系统(2)在式(5)和式(6)成立的条件下至少有3族非退化的周期轨道.因此,可得定理3.

定理3对充分小的a23≠0,系统(2)在Liouville意义下是不可积的.

下面用Lyapunov指数来数值论证系统(2)是否出现Hamilton混沌.

Lyapunov指数是反映一个动力系统是否存在混沌的主要工具[12].若所考虑的动力系统存在正的Lyapunov指数,则可认为系统是混沌的.

对于系统(2),若取参数a12=a23=a34=1,b1=b3=-1,b2=b4=1,则用数学软件Maple计算该系统的最大Lyapunov指数,结果如图1所示.

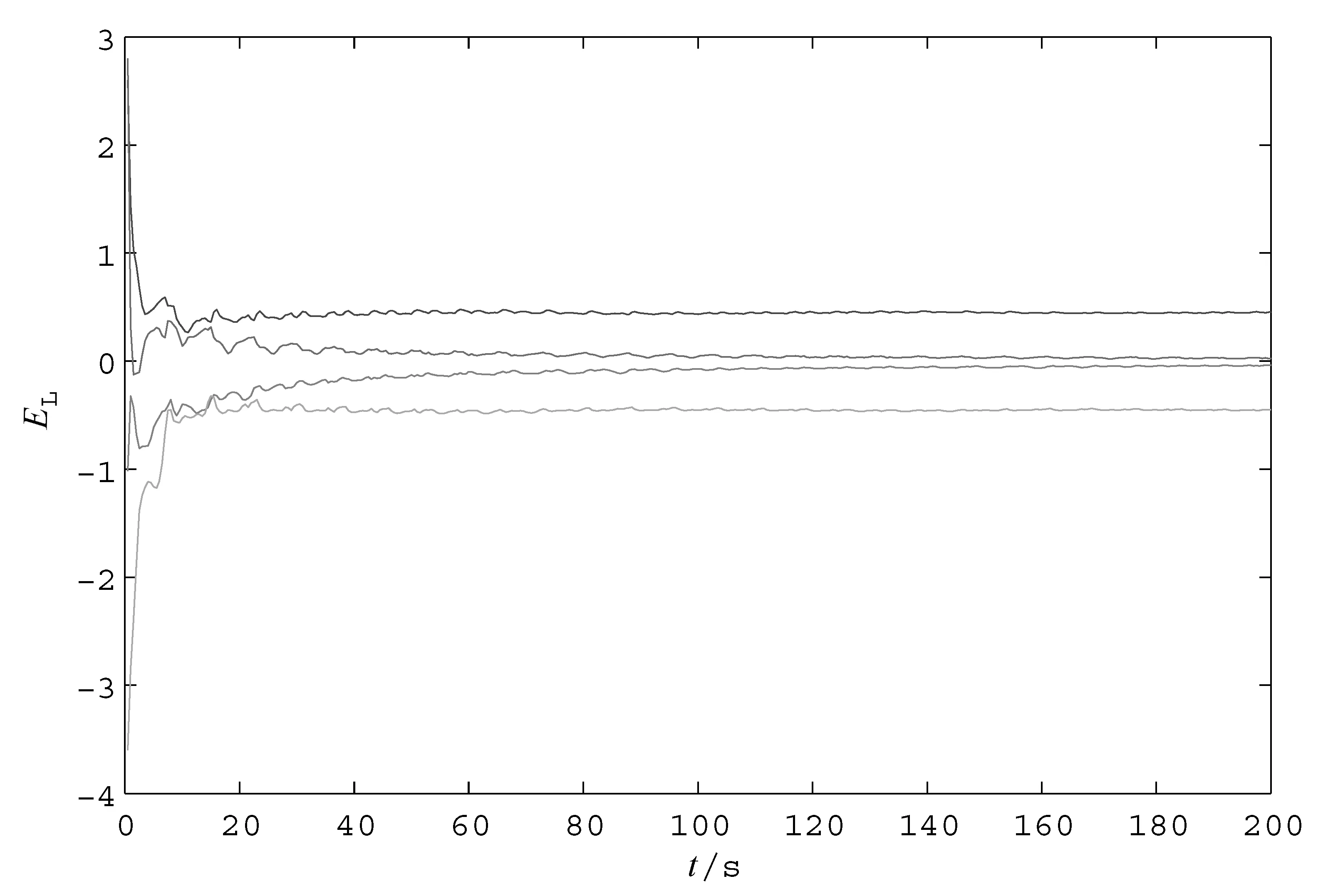
图1 Lyaounov指数

从图1可看到,系统(2)的4个Lyapunov指数中有2个为0,另外2个Lyapunov指数为±0.445.因此,此系统是混沌的.

[1]Hofbauer J,Sigmund K.Evolutionary games and population dynamics[M].Cambridge:Cambridge University Press,1998.

[2]Xia Yonghui.New results on the global asymptotic stability of a Lotka-Volterra system[J].Appl Math Comput,2011,36(1/2):117-128.

[3]Svirezhev Y M.Nonlinearities in mathematical ecology:Phenomena and models:Would we live in Volterra′s world?[J].Ecological Modelling,2008,216(2):89-101.

[4]Upadhyay R K.Observability of chaos and cycles in ecological systems:Lessons from predator-prey models[J].International Journal of Bifurcation and Chaos,2009,19(10):3169-3234.

[5]Duarte P,Fernandes R L,Oliva W M.Dynamics of the attractor in the Lotka-Volterra equations[J].Journal of Differential Equations,1998,149(1):143-169.

[6]Zhao Xiaohua,Luo Jigui.Classification and dynamics of stably dissipative Lotka-Volterra systems[J].International Journal of Nonlinear Mechanics,2010,45(6):603-607.

[7]赵晓华,吴红颖.保守型Lotka-Volterra系统的Hamilton结构与周期解[J].浙江师范大学学报:自然科学版,2007,30(3):246-250.

[8]Picard G,Johnstone T W.Instabillity cascades,Lotka-Volterra population equations,and Hamilton chaos[J].Physical Review Letters,1982,48(23):1610-1613.

[9]李继彬,赵晓华,刘正荣.广义哈密尔顿系统理论及其应用[M].2版.北京:科学出版社, 2007.

[10]Meyer K R,Hall G R,Offin D.Introduction to Hamiltonian dynamical systems and theN-body problem[M].2nd ed.New York:Springer,2009.

[11]Milnor J.Morse theory[M].New Jersey:Princeton University Press,1969.

[12]Ott E.Chaos in dynamical systems[M].2nd ed.Cambridge:Cambridge University Press,2002.

HamiltonianstructureanddynamicsofafourdimensionalLotka-Volterrasystem

ZHAO Xiaohua, DAI Canhua

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

It was studied a four dimensional Lotka-Volterra (LV) system with Hamiltonian structure. The results showed that the LV system had at least three different families of periodic solutions for generic parameters, and it was nonintegrable for smalla23≠0 and Hamiltonian chaos might occur.

Lotka-Volterra system; Hamiltonian structure; periodic solution; Lyapunov exponent; Hamiltonian chaos

1001-5051(2011)03-0241-05

O19;O75.14

A

2010-12-21

国家自然科学基金资助项目(10872183)

赵晓华(1961-),男,云南昆明人,教授,博士.研究方向：动力系统分支与混沌；广义Hamilton系统理论及应用.

(责任编辑 陶立方)