一类新拟移位映射和Möbius带上的吸引子*

俞春叶, 陈凤娟

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

一类新拟移位映射和Möbius带上的吸引子*

俞春叶, 陈凤娟

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

给出了双边符号空间上的一类新拟移位映射,证明它是半符号空间的自同胚,并用这类新拟移位映射刻画了Möbius带上一类映射的混沌动力学性质.

符号动力系统;拟移位映射;Möbius带;吸引子

0 引 言

1967年,Smale[1]构造了著名的马蹄模型,并运用2-符号空间Σ2上的移位映射刻画了它的混沌动力学性质.许多复杂的自映射存在子系统(X,f)与(Σ,σ)拓扑共轭,其中Σ为相应的符号空间,σ为移位映射.

近年来,一些文献给出了不同于传统移位映射的拟移位映射或部分变号移位映射,并用这些拟移位映射刻画了某些自映射的混沌动力学性质[2-4].

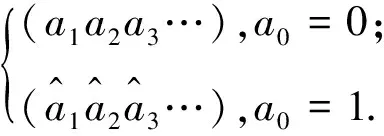
式(1)中

文献[3]用该类映射描述了Cantor集及平面Cantor集上的混沌映射.

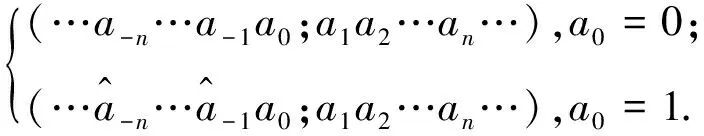
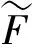
1 一类新的拟移位映射

定义1设集合A={a=(…a-n…a-1;a0a1…an…)∈Σ2|a0=0}⊂Σ2;B={a=(…a-n…a-1;a0a1…an…)∈Σ2|a0=1}⊂Σ2.显然,A∪B=Σ2.称这样的A和B为半符号空间.

定义2D={a=(…a-n…a-2a-1;a0a1a2…an…)∈Σ2|a-1=a0=a1=0}⊂A.

定义3定义一类新的拟移位映射τ3:Σ2→Σ2为：对∀(…a-n…a-2a-1;a0a1a2…an…)∈Σ2,有

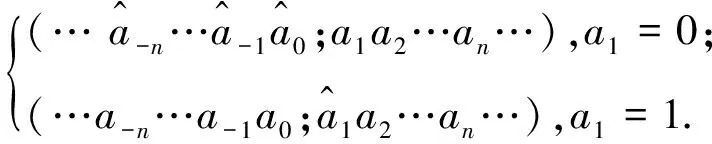
为便于说明，用符号“-1”代替“0”,符号“1”不变.

定义映射ζ:Σ2→Σ2为：对∀a=(…a-n…a-1;a0a1…an…)∈Σ2,有

ζ(a)=(…(a-n×a1)…(a-1×a1)(a0×a1);(-1)a2…an…).

其中，“×”为传统意义上的乘法运算.于是

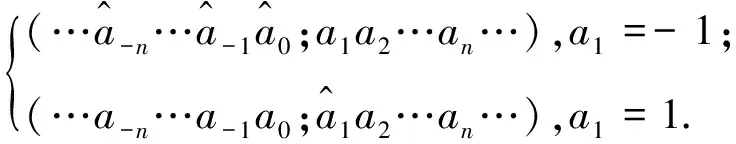
比较式(4)与式(5),得ζ与τ3具有相同的作用.

定理1映射ζ是半符号空间A的自同胚.

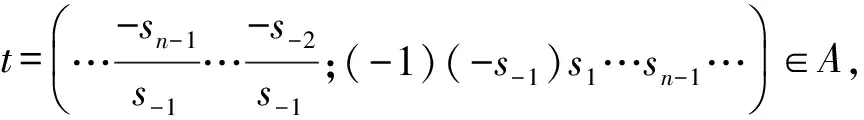
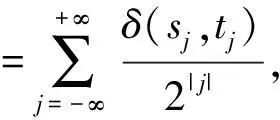
因此，映射ζ在半符号空间A上既是一一映射，又是连续映射，从而映射ζ是半符号空间A的自同胚.定理1证毕.

性质1映射ζ有且仅有不动点a=(…(-1)(-a0)(-1)(-a0);(-1)a0a0a0…),a0∈{1,-1}.

性质2存在同胚映射η:Σ2→Σ2,对∀a∈D⊂A,有σ∘η(a)=η∘ζ(a).

证明 取a=(…a-n…a-2(-1);(-1)(-1)a2…an…)∈D,作同胚映射η满足

η(…a-n…a-1;a0a1…an…)=(…(a-n×a-1)…(a-2×a-1)(a-1×a0);a0a1…an…),

从而

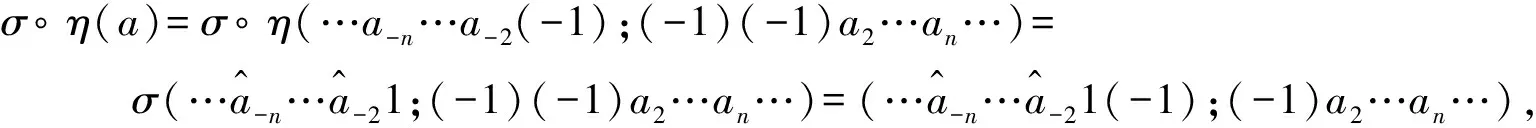
同时

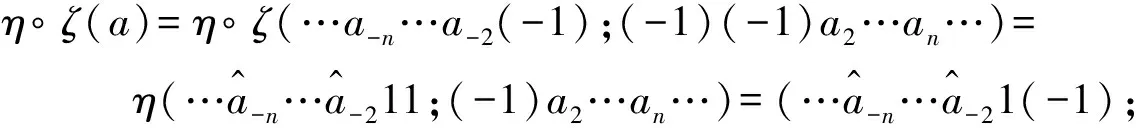
因此,σ∘η(a)=η∘ζ(a).性质2证毕.

2 Möbius带上的奇异吸引子

M={(x,p) |p=reiπ(x+1/2),x∈[-0.5,0.5),r∈[-0.5,0.5)}.

定义

M0={(x,p) |p=reiπx,x∈[0,0.25),r∈[-0.5,0.5)};

M1={(x,p) |p=reiπx,x∈[-0.25,0),r∈[-0.5,0.5)}.

M0与M1为Möbius带M上相接的两部分,如图1所示.

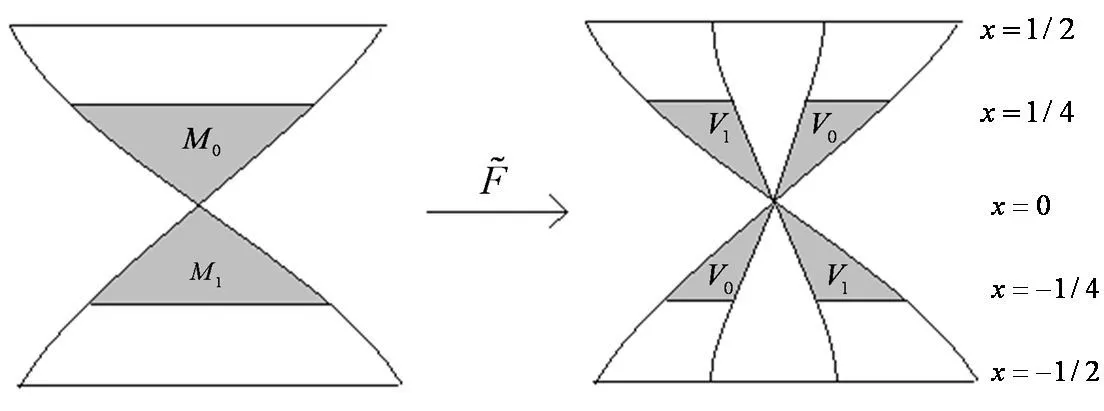
图1 Möbius带及其上映射的作用

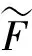
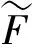
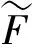
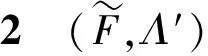
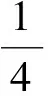
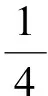
记x0～(s0s1s2…sn…),r0～(…s-n…s-3s-2s-1).类似文献[2]的记法,将三进制展开中的2用1代替,则

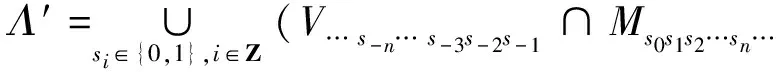
式(7)中:V…s-n…s-3s-2s-1代表r的变化方向;Ms0s1s2…sn…代表x的变化方向.由Λ′的结构及式(7)知,∀q∈Λ′,一定存在唯一的符号序列(…s-n…s-2s-1;s0s1s2…sn…)与之对应,记q～(…s-n…s-2s-1;s0s1s2…sn…).

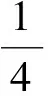
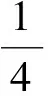
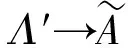
φ(q)=φ(V…s-n…s-3s-2s-1∩Ms0s1s2…sn…)=(…s-n…s-2s-1;s0s1s2…sn…).

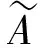
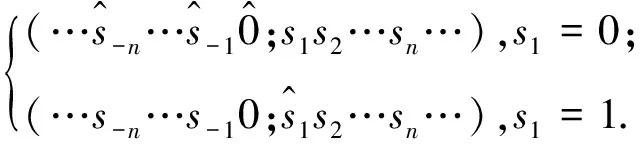
同时

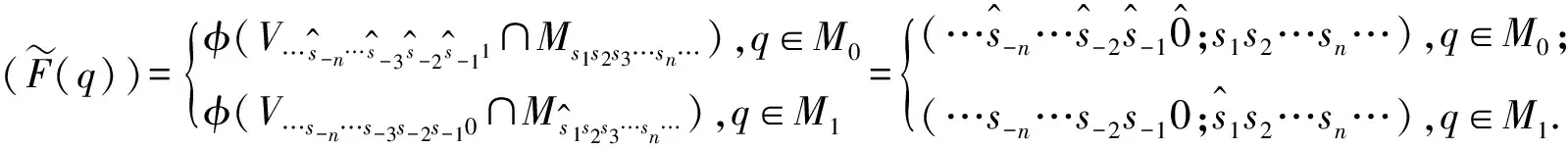
因此,τ3∘φ=φ∘F.定理2证毕.

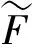
[1]Smale S.Differentiable dynamical systems[J].Bull Amer Math Soc,1967(73):747-817.

[2]陈芳跃,陈凤娟.符号空间的拟移位和Möbius带上的奇怪吸引子[J].应用数学和力学,2003,23(7):747-754.

[3]李明军,李开泰.一类描述混沌映射的符号动力系统[J].高校应用数学学报,1999,14(2):125-129.

[4]麦结华.用5-进制小数描述Smale马蹄映射[J].科学通报,1993,38(21):1432-1435.

[5]韩茂安,邢业朋,毕平.动力系统导论[M].北京:机械工业出版社,2007:310-345.

AclassofnewmodelshiftmapingandattractoronMöbiusstrip

YU Chunye, CHEN Fengjuan

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

A class of new model shift maping was defined in bilateral symbol space. It was showed that the new model shift was a homeomorphism onto itself in a semi-bi-infinite symbolic space. A class of map on Möbius strip corresponding to the model shift was also constructed, and its dynamical behavior was described.

symbolic dynamical system; model shift maping; Möbius strip; attractor

1001-5051(2011)03-0252-04

O189

A

2010-11-17

国家自然科学基金资助项目(10872183)

俞春叶(1986-),女,浙江嘉兴人,硕士研究生.研究方向:微分动力系统.

陈凤娟.E-mail: fjchen@zjnu.cn.

(责任编辑 陶立方)