最大度为6且不含4-圈和7-圈的平面图的边列表和全列表*

姚潇彦

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

本文考虑的图都是简单、有限的无向图．文中未加定义的术语和记号参阅文献［1］．用V(G)，E(G)，F(G)，Δ(G)和δ(G)分别表示平面图G的顶点集、边集、面集、最大度和最小度(在不引起混淆的情况下简记为 V，E，F，Δ 和 δ)．

图G的一个k-边染色是一个映射φ:E(G)→{1，2，…，k}，其中k是整数．若映射φ还满足对于G中的每一对相邻边e和e'，有φ(e)≠φ(e')，则称这个k-边染色是正常的;若G有一个正常的k-边染色，则称G是k-边可染的;G的边色数χ'(G)是使得G是k-边可染的最小的整数k;称映射L为图G的一个边列表，如果它给每条边e∈G一个颜色集合L(e);若有一个正常的边染色φ，使得每一条边e满足φ(e)∈L(e)，则称G是L-边可染的，或称φ是G的一个L边染色;若对任意表L和每条边e∈E(G)，都有|L(e)|≥k，且G是L边可染的，则称G是k-边可选的．G的边列表色数χ'l(G)是使得G是k-边可选择的最小的整数k．类似地，可定义同时染顶点和边的G的全列表色数χ"l(G)．由定义可直接得到χ'l(G)≥χ'(G)≥Δ(G)和 χ"l(G)≥χ"(G)≥Δ(G)+1．

下面是著名的边列表染色和全列表染色猜想:

猜想1 如果G是一个多重图，则:1)χ'l(G)= χ'(G);2)χ"l(G)= χ"(G)．

对于二部重图、奇阶完全图、多重圈、外平面图，已证明猜想1的1)成立．文献［2］证明了对于Δ≥12可嵌入非负特征曲面上的图，猜想1成立;文献［3］证明了对于最大度至少为7且不含4-圈的平面图及最大度至少为6且不含4-圈和6-圈的平面图，猜想1成立．

本文研究Δ≥6的平面图的边列表染色和全列表染色问题，得到以下结果:

定理1 若G是Δ≥6且没有4-圈和7-圈的平面图，则G是6-边可选的和7-全可选的．

1 引理

方便起见，先引进一些定义和记号．把度为k或度不小于k或度不大于k的点(或面)分别称做k-点(面)，k+-点(面)，k--点(面);一个面f的度d(f)，是指关联f的边的条数，其中割边被计算2次．用nv(f)表示任意一个关联f的点v经过f的闭途径的次数．

假设定理1不成立，并设G是定理1的一个使σ(G)=|V|+|E|最小的反例，即G本身不是6-边可选的和7-全可选的，但它的每个真子图都是6-边可选的和7-全可选的，则G有以下几个性质:

引理1 G是连通的．

引理2 设∀e=uv∈E．若6+-点相邻，3-点只与 5+-点相邻．

引理3 G不含2-交替圈．

由G的极小性容易证明引理1，引理2和引理3的证明可参阅文献［4］．

引理4 令G'是G中所有关联2-点的边导出的子图，则G'是一个森林．

设T是G'中的一棵极大树，由引理2知，T的所有叶子都是6+-点，由归纳法容易证明G'中存在一个饱和所有2-点的匹配M．如果给每个极大树配一个极大匹配，并设v是G中任意一个2-点，那么称v的被匹配饱和的邻点为v的master．

引理5 G具有以下性质:

2)每个关联3-面的面是5-面或8+-面;

3)若一个2-点关联一个3-面，则它关联的另一个面是6-面或9+-面;

4)若一个3-点关联一个3-面和一个5-面，则它关联的另一个面是8+-面;

5)设 f1，f2，f3是v关联的面，且依顺时针方向排列，如果f1，f3都是3-面，那么 f2是8+-面．

证明:1)，2)和3)易证，下证4)和5)．

4)设v是一个3-点，f1，f2，f3是v关联的3个面，不失一般性，假设它们是依顺时针方向排列的，且d(f1)≤d(f2)，其中 f1是 5-面，f3是 3-面．用反证法．设 d(f1)=d(f2)=5，且 f1=［vuu1u2u3］，f2=［vuv1v2v3］，若 f1和 f2正常相邻，则会产生一个 7-圈 C=［uu1u2u3v3v2v1u］．事实上，{u1，u2，u3}∩{v1，v2，v3}=Ø．否则，若 u1=v1，则 u 是一个 2-点，与引理 2 矛盾;若 u2=v1，则会产生一个 4-圈 C=［v1(=u2)u3vuv1］;若u3=v1，则会产生一个 4-圈 C=［v1(=u3)u2u1uv1］．所以 v1≠u1(u2，u3)．类似地可验证v2≠u1(u2，u3)，v3≠u1(u2，u3)．所以，f1和f2不可能正常相邻，但 f1和 f2也不可能非正常相邻．不然，u是一个2-点，与引理2矛盾．若d(f2)=6，可类似证明会产生4-圈或7-圈，得到矛盾．所以，若d(f1)=5，则由 d(f1)≤d(f2)可得 d(f2)≥8．

5)设v是f1，f2，f3的公共点，u1，u2和u3，u4分别是f1和f3关联的另外2个顶点，且按顺时针方向排列．对u2，u3分3种情形讨论:

①d(u2)≥3，d(u3)≥3．因为G不含4-圈，所以f2不可能是3-面或4-面．事实上，G也不是5-面或6-面．否则，若 f2=［vu2x1x2u3v］是 5-面，则 C=［vu1u2x1x2u3u4v］是 7-圈;若 f2=［vu2x1x2x3u3v］是 6-面，则C=［vu2x1x2x3u3u4v］是7-圈．但 G 不含7-圈，所以 f2是 8+-面．

②d(u3)≥3，d(u2)=2，或 d(u2)≥3，d(u3)=2．由对称性，不妨考虑 d(u2)≥3，d(u3)=2．由引理4的2)知，f2一定是 5+-面．若 f2=［vu2x1u4u3v］是 5-面，则会产生一个 4-圈 C=［vu2x1u4v］;若 f2=［vu2x1x2u4u3v］是 6-面，由于 G 不含4-圈，所以 u1≠x1且 u1≠x2，则 C=［vu1u2x1x2u4u3v］是7-圈．但 G 不含7-圈，所以 f2是8+-面．

③d(u2)=d(u3)=2．由引理4的2)知，f2一定是5+-面．若 f2=［vu2u1x1u4u3v］是5-面，则会产生一个4-圈 C=［vu2u1u4v］;若 f2=［vu2u1x1u4u3v］是6-面，则会产生一个4-圈 C=［vu1x1u4v］．综上所述，f2是8+-面．引理5证毕．

2 定理1的证明

设G是定理1的一个使σ(G)=|V|+|E|最小的反例．以下将运用Discharging方法导出完成定理1证明所需要的矛盾．首先，给G的任意的x∈V∪F分配初始权ch(x)=d(x)－4，由平面图的欧拉

以下将定义一个权转移规则，重新分配点和面的权，并设ch'(x)是重新分配点和面的权后元素x∈V∪F的新权．将要证明对每个 x∈V∪F都有一方面，由于权的转移只是在同一个图的点和面之间进行，权的总和应该保持不变，因此得到-8≥0，即得到了证明定理1所需要的矛盾．

权转移规则如图1所示．

R3:每个5+-点与其关联的3-面各

R4:每个5+-面向每个关联的点转

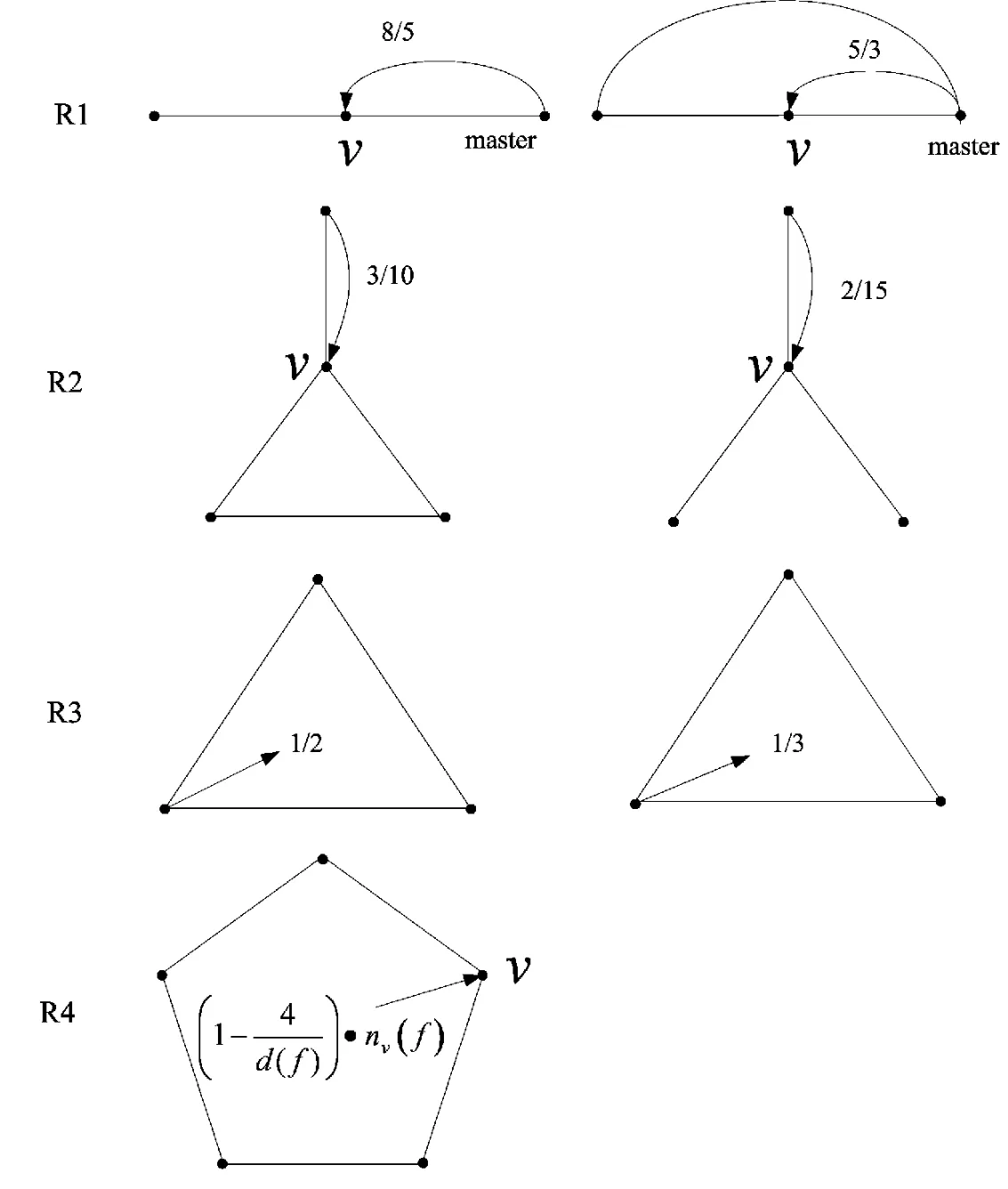
图1 权转移规则图

下面只需验证对于每个x∈V∪F都有ch'(x)≥0．

先考察面的新权．

因为G是简单图，所以对每个面f都有d(f)≥3．又由权转移规则知:若d(f)≥4，则ch'(f)≥0．所以，下面只需验证3-面．

设f为3-面，则ch(x)=-1，由引理2知，f至多关联1个3--点．

若f关联一个3--点，则由引理2知，其余2个均为5+-点，由R3知0．

设v为3-点，则ch(v)=-1，由引理5的1)知，f至多关联1个3-面．

若v关联1个3-面，则由引理4的2)和引理4的4)知，v关联的另2个面要么是5-面和8+-面，要

其次考察点的新权．

设 v为 2-点，则 ch(v)=-2．

若v关联一个3-面，则由引理5的3)知，v关联的另一个面是6+-面，由R1和 R4知，ch'(v)=

设v为4-点，则ch'(v)=0，由引理5的1)知，v至多关联2个3-面．又由权转移规则知，v只向3-面转权．所以，当v关联2个3-面时 ch'(v)最少．由引理5的5)知，v还关联2个8+-面，所以 ch'(v)≥

设t是v关联的3-面的个数．称关联3-面的3-点为坏3-点．用b3(v)表示v相邻的坏3-点的个数．

设v为5-点，则ch'(v)=1，由权转移规则知，v只向3-面和3-点转权，由引理5的1)知，v至多关联2 个3-面．

1)t=0，此时v只向3-点转权，且至多与5个坏3-点相邻，则

3)t=2，此时v至多与1个坏3-点相邻，由引理5的5)知，v至少关联1个8+-面，则ch'(v)≥1-

设v为6-点，则ch(v)=2．下面将根据v与2-点相邻的情形对6-点的新权逐一进行验证．

1)v是一个2-点 u的 master．

①v不与三角形关联，那么v至多关联2个3-面．

②v与三角形关联，由于G不含4-圈，故v至多关联3个3-面．

t=1，此时v至多与4个坏3-点相邻．若b3(v)=0，则v只向正常3-点转权，且至多与4个坏3-点相b3(v)=2，则v至少关联1个8+-面和1个6+-面，此时v至多与2个正常3-点相邻，从而ch'(v)≥2-1个正常3-点相邻，从而少关联3个8+-面，此时v不与正常3-点相邻，从而

t=2，此时v至多与2个坏3-点相邻．若 b3(v)=0，则由引理5知，v至少关联1个6+-面，从而;若b3(v)=1，则由引理5知，v至少关联1个8+-面，此时v至多与1个正常3-点相邻，从而至少关联2个8+-面，从而

t=3，此时v不需要向3-点转权，由引理5的5)知，v至少关联3个8+-面，从而

2)v不是任意2-点的master，此时v至多与3个3-面关联．

①t=0，此时v只向3-点转权，且至多与6个坏3-点相邻，因此

④t=3，此时v不向任何3-点转权，且由引理5的4)知，v至少关联3个8+-面，因此ch'(v)≥2-

至此，对∀x∈V∪F，ch'(x)≥0都已得到验证．定理1得证．

［1］Bondy J A，Murty U S R．Graph theory［M］．Berlin:Springer，2008．

［2］Borodin O V，Kostochka A V，Woodall D R．List edge and list total colorings of multigraphs［J］．J Combin Theory，1997，71(2):184-204．

［3］Liu Bin，Hou Jianfeng，Liu Guizhen．List edge and list total colorings of planar graphs without short cycles［J］．Information Processing Letters，2008，108(6):347-351．

［4］Wang W F，Lih K W．Structural properties and edge choosability of planar graphs without 6-cycles［J］．Combin Probab Comput，2001，10(3):267-276．