条形纳米通道中奇特的钠选择性*
吴林松, 吴锋民, 陆杭军, 何俊霞, 聂雪川, 寇建龙
(浙江师范大学凝聚态物理研究所,浙江金华 321004)
0 引言
纳米孔道的离子选择性一直受到广泛关注[1-7],主要是因为:在生物体系中存在许多具有离子选择性的孔道(离子通道),这些离子通道与很多重要的生命活动过程有关,而其选择机制还没有完全被理解.早期研究是假定在K+通道结构固定不变的条件下,认为通道中的羰基构成的水合壳层很适合K+,而对Na+来说距离太远,不能形成Na+的水合层,因此对Na+来说很不适合,所以K+比Na+的通透率大[8].但是这个假设并不合理,因为这种管壁具有一定程度的柔性,必须考虑热扰动,其残基振动幅度可以达到约0.07 nm[4].现在,有研究认为K+通道的选择性主要是由于羰基配体之间的排斥力所引起的.最近,有研究人员[9]模仿Na+通道,通过在碳纳米管上修饰羰基((9,9)型纳米管),分别实现了K+和Na+的选择.研究发现:米管内存在着一定的离子选择性;同时,离子的选择性行为被认为是与纳米管本身的几何限制结构和离子的第1壳层配体有关[10-16].另外也有科学家[17]运用带电的管道实现了多种离子的选择.尽管离子分离技术已经有了一定的发展,但是仍然有很多难题需要攻克.例如:K+和Na+2种单价离子的分离;如何在保证选择性的前提下提高通透效率等等,这些问题是设计过滤膜的关键基础问题.本文通过对石墨面构成的条形纳米通道的离子选择性行为的研究来探讨纳米孔道的离子选择机制,同时希望设计出具有离子选择性并有高通透效率的纳米通道.条形纳米通道相对于碳纳米管来说离子在通道中的束缚明显减少,但是研究表明它的选择性行为并未出现消退.因此,这种孔道可以让离子的输运速率大大加快.这种纳米通道构成的膜在离子分离与海水淡化中具有更大的优势.
1 计算方法和模型
模拟系统如图1所示.图1中条形纳米通道由上下2块长为2.11 nm、宽为4.97 nm的单层石墨片构建而成,中间的条形纳米通道由2块长为2.11 nm,宽为4.97 nm的单层石墨片构成,嵌在由2块石墨片构成的膜中,膜两边为离子溶液.定义2块石墨片之间的距离为d.本文模拟了4种不同宽度(即不同d值)的条形纳米通道的离子选择性,d分别为:0.88,0.90,0.95,1.00 nm.模拟水盒子大小设定为:Lx=6.00 nm,Ly=5.11 nm,Lz=5.00 nm.把条形纳米通道沿x方向嵌入由石墨片构成的膜中,膜把水盒子分成左右2部分.其两侧充满水分子,水分子采用tip3p[18]模型,水中共加入 30 个 Na+,30 个 K+,60 个 Cl-,构成离子溶液(KCl和 NaCl的浓度约为0.46 mol/L).沿条形纳米通道方向施加0.01 V/nm的电场,其大小与生物系统中的电场相接近.
本文采用分子动力学软件GROMACS 4.0.7[19]进行模拟,采用GROMACS自带的力场和NVT系综,Berendsen控温法,温度设定为T=300 K.为了便于研究问题,在整个模拟过程中条形纳米通道与膜固定不动.其碳原子的范德华参数为:εC-C=0.361 2 kJ/mol,σC-C=0.34 nm.为了减少计算量,短程相互作用势能截断半径rc=1.0 nm.电相互作用采用PME算法[20].本文所有模拟采用周期性边界条件,时间步长为2 fs,每ps保存1次数据,模拟时间为305 ns,模拟数据分析从第6 ns开始.
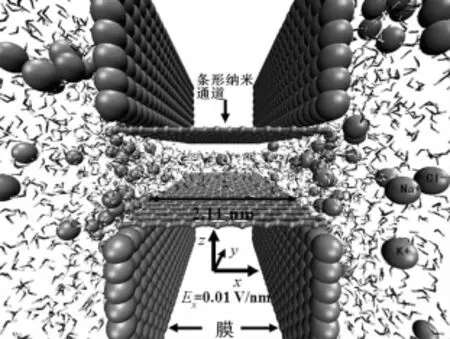
图1 模拟系统示意图
2 结果与讨论
当沿条形纳米通道方向施加电场后,离子会在电场的作用下通过条形纳米通道.分别对不同间距的条形纳米通道的离子通透情况进行模拟研究,其结果如表1所示.表1表示的是后300 ns内阳离子(K+,Na+)沿着x方向的流动情况.其中ΔNa+和ΔK+分别表示Na+和K+在条形纳米通道中朝+x方向通过的个数与朝-x方向通过的个数之差.表1最后一列(ΔNa+/ΔK+)则是2种离子的通过比率.从表1可以看出,除了d=1.00 nm的系统外,Na+比K+更容易通过条形纳米通道,表现出明显的钠选择性.特别是d=0.88 nm这个系统,Na+和K+的通过比率可达到6.当d逐渐增加时,2种阳离子的流量都会增大.同时,2种阳离子通过比率逐渐趋向于1,离子的选择性逐渐减弱.
笔者分析了这4个系统中K+和Na+沿着x方向的概率密度分布(ρ).下面是离子概率密度的计算方法:将条形纳米通道沿着x方向(2.11 nm)分成1 000份,此时离子的概率密度可以通过下面的公式进行计算:
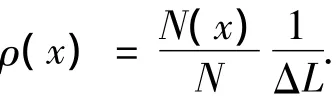
其中:ΔL表示1份的长度;N(x)是指模拟的N帧中在x位置所在的这份出现的离子总数.
2种离子的概率密度分布具体结果如图2所示.由图2可知,4种孔道中Na+的概率密度要高于K+的概率密度.换句话说,Na+更容易进入孔道.所以,这几个系统都有一定的钠选择性.

表1 不同间距的条形纳米通道的离子通透情况模拟结果
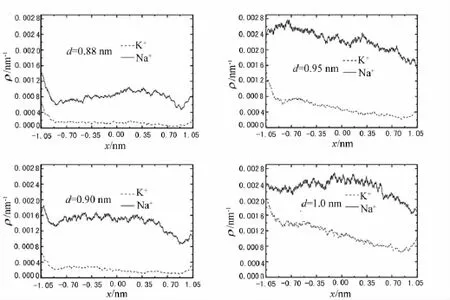
图2 2种离子沿着x方向的离子概率密度分布示意图
K+通道的K+/Na+通过比率高达1 000∶1,而钠孔道的Na+/K+选择比率也能达到500∶1.离子进入生物孔道中将脱去一定的配体数,而第1壳层配体数的变化对通道的选择性有很大的影响.Na+和K+在宏观水相中的第1壳层平均配体数分别为5.72和6.88个.Na+在宏观水相中出现5个配体数的概率约为21%,6个配体数的概率约为69%.另外,K+在宏观水相中配体数分布主要集中在6(约为30%),7(约为41%),8(约为 20%).
K+和Na+在通道中的第1壳层配体数概率分布如图3所示.从图3容易得出d=0.88 nm的系统中,Na+的第1壳层配体数比K+更接近于宏观水相中的分布.需要说明的是,一种离子在孔道中的配体数分布越接近宏观水相中的分布,那么该孔道就越有利于这种离子通过.因此,笔者看到d=0.88 nm的系统中Na+比K+流通量大得多,形成了Na+选择性.同时,从图3中容易发现,随着通道管径的增大,2种离子的第1壳层配体数分布都会越来越接近于宏观水相中的分布.换句话说,孔道的管径增大,2种离子都会比较容易通过.从而得到当d=1.00 nm时孔道的选择性几乎消失.
进一步分析Na+和K+在条形纳米通道内沿着x方向的第1壳层平均配体数概率分布,结果如图4所示,bulk K+和 bulk Na+分别指宏观水相中的第1壳层平均配体数.
由图4 可知,d=0.88,0.90,0.95 nm 这 3 个系统的Na+第1壳层平均配体数分别约为:5.33,5.48,5.56.K+在这 3 个系统中的平均配体数分别约为5.63,5.98,6.47.而宏观水相中Na+和K+的第1壳层平均配体数则分别为5.72和6.88.由这些结果可知,Na+相对于 K+来说更接近于它在宏观水相中的分布.
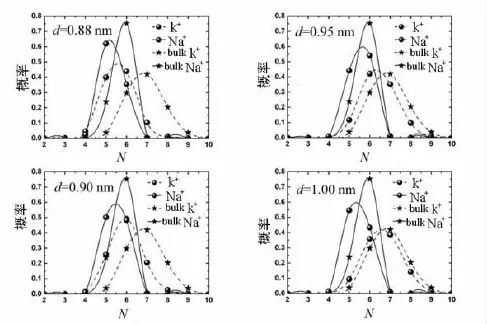
图3 2种离子在4种管内和在宏观水相中的第1壳层配体数概率分布示意图
笔 者 发 现,d=0.88,0.90,0.95 nm 系统存在着Na+选择性.而从 d=1.00 nm开始,发现K+和Na+的平均配体数分别为6.63和5.44,可以说都比较接近宏观水相的配体数.因此该系统没有出现离子选择性.
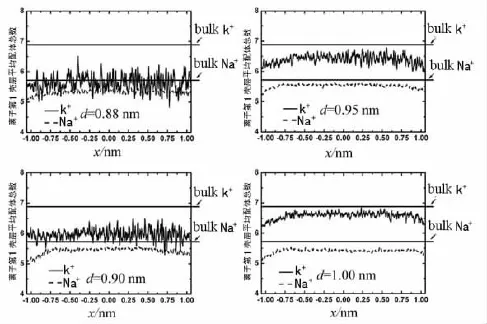
图4 Na+和K+沿着x方向的第1壳层平均配体数分布图
为了更清楚地说明这几种条形纳米通道的选择性,笔者同时探究了电场强度对孔道离子选择性的影响.将选择性最强的系统(d=0.88 nm)通过增大电场来观察其钠选择性行为的变化,具体结果如图5所示.
从图5中容易发现,随着电场强度的增大,条形孔道中的钠选择性行为在逐渐减弱.同时通透比率的变化并不是随着电场增大而线性减小.引起通透比率减小的主要原因是由于电场强度增大,相应离子的驱动力就会增大,当驱动力增大到一定程度后,K+也变得很容易通过,因此,通透比率会逐渐减弱.
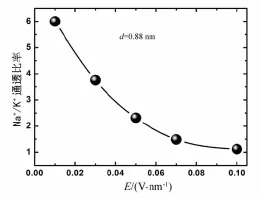
图5 系统在不同电场条件下的通透比率分布
3 结论
通过分子动力学模拟,发现了条形纳米通道中存在离子选择性.而这种选择机制主要是由于2种离子在通道内配体数与它们在宏观水相中第1壳层的配体数分布不一样引起的.另外,通过模拟发现,孔道的钠选择性会随着外加电场的逐渐增大而减小.结果分析认为,这种条形纳米通道具备一定的优势:1)这种孔道相对来说更加简单,也更容易让人们修饰相应的残基;2)d=0.88 nm系统只要施加E=0.01 V/nm的驱动就能驱动离子通过孔道,而且K+和Na+通过比率可以达到6.但是对于柱形无修饰的管道,要达到这个选择比率非常困难,因为柱形纳米通道中要存在这种选择比率的孔道,其管径非常小,需要极大的驱动力才可以让离子通过孔道.因此,有理由相信条形纳米通道的选择性研究对未来离子分离的实验和理论研究都会有帮助.
[1]Benèche S,Roux B.Energetics of ion conduction through the K+channel[J].Nature,2001,414:73-77.
[2]Benèche S,Roux B.A microscopic view of ion conduction through the K+channel[J].Proc Natl Acad Sci USA,2003,100:8644-8648.
[3]Noskov S Y,Roux B.Importance of hydration and dynamics on the selectivity of the KcsA and NaK channels[J].J Gen Physiol,2007,129:135-143.
[4]Noskov S Y,Berneche S,Roux B.Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands[J].Nature,2004,431:830-834.
[5]Dudev T,Lim C.Determinants of K+vs Na+selectivity in potassium channels[J].J Am Chem Soc,2009,131,8092-8101.
[6]Dudev T,Lim C.Effect of carboxylate-binding mode on metal binding/selectivity and function in proteins[J].Acc Chem Res,2007,40:85-93.
[7]Thomas M,Jayatilaka D,Corry B.The predominant role of coordination number in potassium channel selectivity[J].Biophys J,2007,93:2635-2643.
[8]Hille B,Armstrong C,MacKinnon R.Ion channels:From idea to reality[J].Nat Med,1999,5:1105-1109.
[9]Gong X J,Li J C,Xu K,et al.A controllable molecular sieve for Na+and K+ions[J].J Am Chem Soc,2010,132:1873-1877.
[10]Beckstein O,Tai K,Sansom M S P.Not ions alone:barriers to ion permeation in nanopores and channels[J].J Am Chem Soc,2004,126,14694-14695.
[11]Bostick D L,Brooks Ⅲ C L.Selectivity in K+channels is due to topological control of the permeant ion's coordinated state[J].Proc Natl Acad Sci USA,2007,104:9260-9265.
[12]Bostick D L,Arora K,Brooks Ⅲ C L.K+/Na+selectivity in toy cation binding site models is determined by the‘Host’[J].Biophys J,2009,96:3887-3896.
[13]Song C,Corry B.Intrinsic ion selectivity of narrow hydrophobic pores[J].J Phys Chem B,2009,113:7642-7649.
[14]Shao Q,Zhou J,Lu L H,et al.Anomalous hydration shell order of Na+and K+inside carbon nanotubes[J].Nano Lett,2009,9:989-994.
[15]Joseph S,Mashl R J,Jakobsson E,et al.Electrolytic transport in modified carbon nanotubes[J].Nano Lett,2003,3:1399-1403.
[16]Peter C,Hummer G.Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations[J].Biophys J,2005,89:2222-2234.
[17]Sint K,Wang B Y,Kral P.Selective ion passage through functionalized graphene nanopores[J].J Am Chem Soc,2008,130:16448-16449.
[18]Jorgensen W L,Chandrasekhar J,Madura J D,et al.Comparison of simple potential functions for simulating liquid water[J].J Chem Phys,1983,79:926-935.
[19]Spoel D van der,Lindahl E,Hess B,et al.GROMACS:Fast,flexible,and free[J].J Comp Chem,2005,26:1701-1718.
[20]Darden T,York D,Pedersen L.Particle mesh Ewald:An N.log(N)method for Ewald sums in large systems[J].J Chem Phys,1993,98:10089-10092.

