一类4维Lotka-Volterra系统的Hamilton结构及动力学*

赵晓华， 戴灿华

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

本文涉及的Lotka-Volterra系统是指下面的常微分方程组:

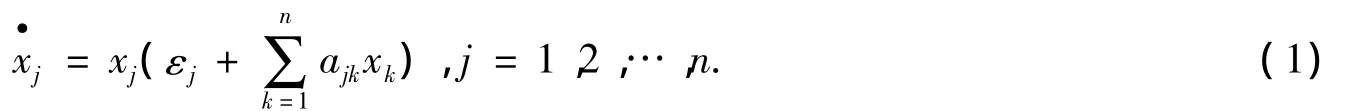
式(1)中:xj表示第j个物种的种群密度;A=(ajk)称为作用矩阵，表示物种间的相互作用关系;εj是与环境相关的参数．

自19世纪20年代Lotka和Volterra分别在研究化学反应和生物问题时提出上述Lotka-Volterra(LV)系统以来，方程组(1)已经被广泛应用于物理、化学、生物、动态博弈论、经济和其他的社会科学中，成为应用数学领域中一个重要的微分方程模型，还被应用于许多热门学科，如神经网络、生物反应、细胞演化和病毒传播等［1-6］，LV系统受到数学及其他学科领域的关注越来越多．在过去的80多年里，对LV系统的理论及应用研究成果大量涌现［7-8］．

但是，除了2维的Lotka-Volterra系统的动力学性质和一些特殊类型的高维Lotka-Volterra系统已分析清楚外，一般的高维Lotka-Volterra系统的动力学性质还远远没有弄清楚，有待深入研究．

研究表明，Lotka-Volterra系统的动力学性质和它的作用矩阵的代数性质有着密切的关系．根据作用矩阵A的不同性质，Lotka-Volterra系统可分为3类［5］(定义1)．

定义1 具有作用矩阵A=(aij)的Lotka-Volterra系统称为:

1)合作型(或竞争型)，如果对任意 i≠j，aij≥0(aij≤0);

2)保守型，如果存在一个正对角矩阵D＞0，使得AD是反对称的;

3)耗散型，如果存在一个正对角矩阵D＞0，使得在二次型意义下AD≤0．

对于耗散型系统，考虑到模型的实际应用，更值得研究的是稳定耗散系统，即作用矩阵A及其对非零元素的小扰动所得的矩阵˜A均为耗散型．

以往的研究主要涉及合作(或竞争)型LV系统，对保守型和耗散型系统的研究相对较少［5-7］．其中特别值得注意的是1998年Duarte等在文献［5］中对这两类系统的研究，他们证明:保守型LV系统若存在正平衡点，则它具有广义Hamilton结构，可以表示为Poisson流形上的广义Hamilton系统;而具有正平衡点的稳定耗散LV系统存在一个整体吸引集，其上的动力学控制方程是一个较低维数的具有广义Hamilton结构的保守型LV系统．关于Hamilton和广义Hamilton系统的相关知识可参阅文献［9-10］．

根据Duarte等的这些结论可以得出，若这个吸引集是单点集，则原LV系统是全局渐进稳定的;若吸引集不是单点集，则需进一步研究吸引集上的子系统的轨道性质．因此，为了弄清稳定耗散系统在吸引集上的动力学性质，本质上就是要研究具有广义Hamilton结构的保守型LV系统的动力学性质．

本文研究了一类具有广义Hamilton结构的4维保守型LV系统，这个系统包含至少3族周期轨道，而对一般的参数是不可积的，并且会出现Hamilton混沌．进而也表明:一般而言，稳定耗散LV系统吸引集的结构可能非常丰富而复杂，值得深入系统地研究．

1 Hamilton结构及平衡点稳定性分析

本文考虑如下的4维Lotka-Volterra系统:

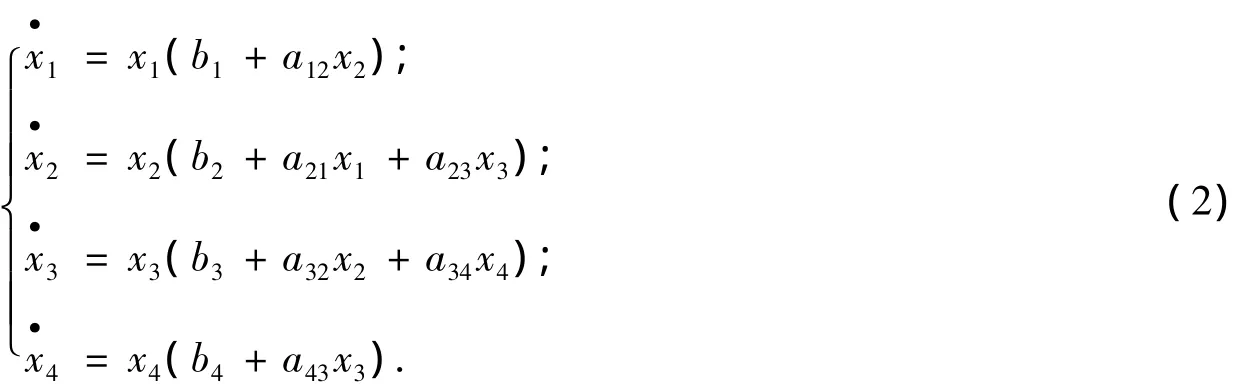
对应的作用矩阵为

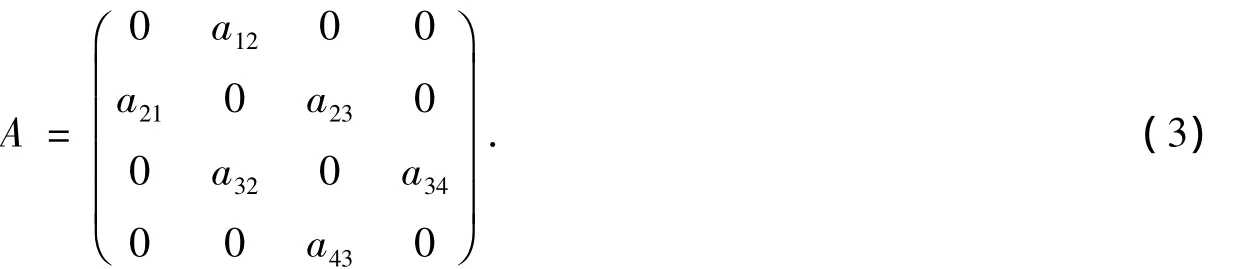
式(3)中:已被标出的元素aij≠0;aijaji＜0．考虑到系统(2)的特殊结构及实际应用背景，只对不变区域

在假设条件aijaji＜0下，系统(2)实际上是一个保守型系统，因为可取对角矩阵D=diag(d1，d2，d3，d4)的对角元素为

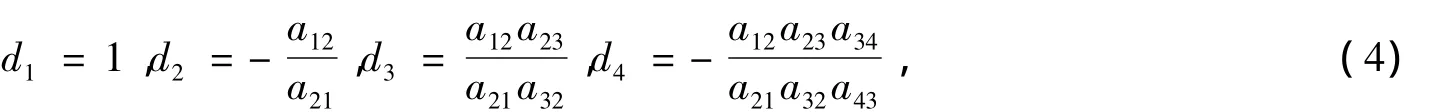
则可使DA为反对称矩阵．进一步，容易验证变换xj→djxj保持系统(2)的形式不变，但作用矩阵变为DA，为反对称矩阵．

因此，不失一般性，直接假定系统(2)的作用矩阵(3)满足以下条件:

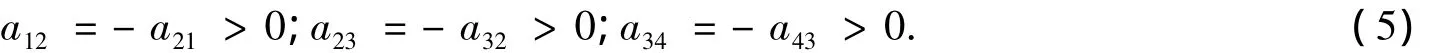
容易验证，若参数 bj(j=1，2，3，4)满足条件

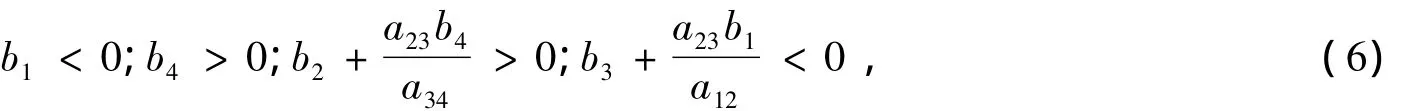
则系统(2)存在唯一正平衡点

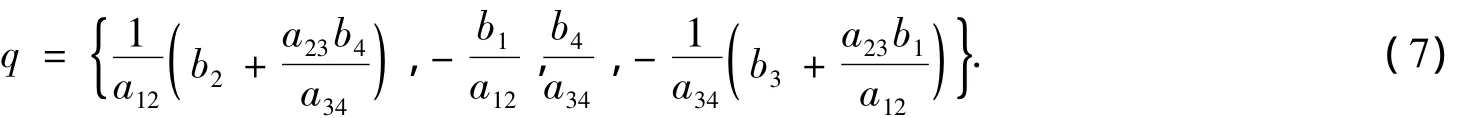
另一方面，在光滑函数空间C∞(R4+)上定义Poisson括号{·，·}为

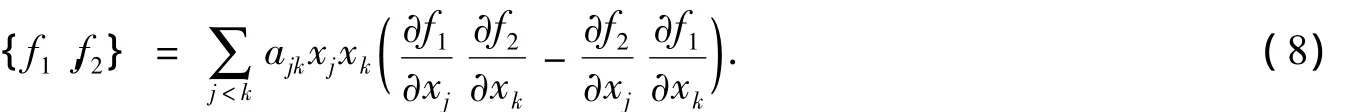
式(8)中，A=(ajk)是满足条件式(5)的系统(2)的作用矩阵．根据辛流形及其上定义的Hamilton系统的理论［9］，直接验证可知{R4+，{·，·}}构成一个4维辛流形，并且有命题1成立．

命题1 在假设式(5)和式(6)成立的情况下，LV系统(2)是4维辛流形{R4+，{·，·}}上的 Hamilton系统，可将系统(2)改写为如下Hamilton形式:

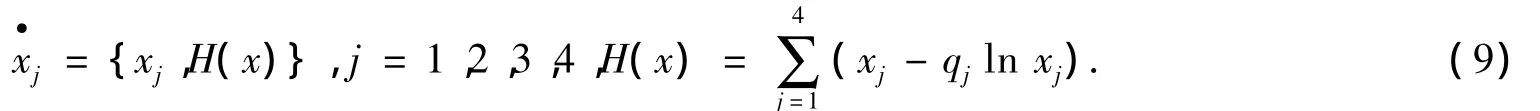
作为Hamilton系统的重要性质之一，Hamilton函数H(x)是LV系统(2)的首次积分，即H沿着系统DH(q)=0，并且Hess矩阵D2H(q)正定，从而根据Dirichlet稳定定理［10］可证得命题2．

命题2 在假设式(5)和式(6)成立的条件下，LV系统(2)的正平衡点q是Lyapunov稳定的．

最后，利用 Morse引理［11］得:对任意 h＞0，水平集 Mh={x∈R4+|H(x)-H(q)=h}拓扑等价于一个3维球面S3．

2 周期轨道

为进一步研究系统(2)的周期解，先介绍下面的Lyapunov中心定理［10］．

引理1(Lyapunov中心定理) 设(M，Ω)是一个2n维辛流形，XH是定义在M上的Hamilton向量数，则存在XH的一个过平衡点q的2维不变流形，其上充满围绕q的周期轨道，它们的周期随着轨道逼

对于系统(2)的唯一正平衡点q，简单计算即可得到其相应的特征方程为

式(10)中:

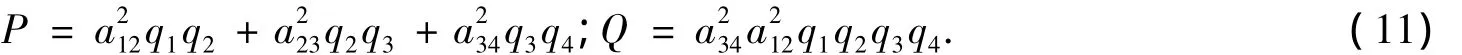
由式(5)和式(6)知 P ＞0，Q ＞0，Δ =P2-4Q ＞0．于是可得命题3．

命题3 在式(5)和式(6)成立的条件下，系统(2)在正平衡点q处的特征方程(10)有2对简单共轭纯虚根，分别为:

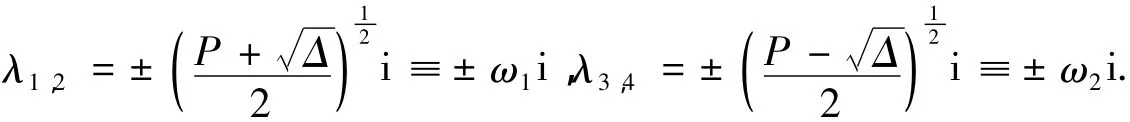
定理1 在式(5)和式(6)成立的条件下，系统(2)至少存在1个过平衡点q的2维不变子流形Π1，数，则存在另一个过q的2维不变流形Π2，其上充满围绕q的周期解，随着这些周期解收缩到q，其相应

系统(2)除了以上周期解外，还可能存在其他周期解．

容易验证，若系统(2)中的a23=0，但式(5)和式(6)中的其他式子仍满足，则系统变为2个独立的2维LV系统:

此时系统是可积的，并有2个独立的首次积分:

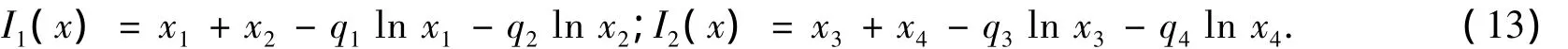
而且在平衡点q处的特征值为2对简单纯虚根:

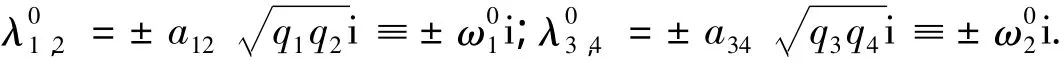
因此，系统(12)的轨道由2个子系统的轨道(均为周期轨道)组合而成，分布于I1(x)和I2(x)确定的水平集上，这个水平集由轨道的初值确定，拓扑等价于2维环面S1×S1，仅当2个子系统解的周期之比为有理数时，对应的4维系统(12)的解才是周期解，否则为拟周期环面解．

特别地，若(φ1(t，I1)，φ2(t，I1))和(φ3(t，I2)，φ4(t，I2))分别是 2 个子系统的周期解，则(φ1(t，I1)，φ2(t，I1)，q3，q4)和(q1，q2，φ1(t，I2)，φ2(t，，I2))就是对应 4 维系统(12)的 2 个周期解，而且易证它们都是Hamilton系统(2)在参数a23=0时的椭圆型周期解．根据Hamilton系统的性质，当a23≠0充分小时，Hamilton系统(2)仍然存在2个与它们对应的周期解．

定理2 在式(5)和式(6)成立的条件下，当a23≠0充分小时，系统(2)存在2族分别对应于(φ1(t，，I1)，φ2(t，I1)，q3，q4)和(q1，q2，φ1(t，I2)，φ2(t，，I2))的周期解．

3 不可积性与Hamilton混沌

根据Hamilton系统中的Liouville完全可积性定义［9-10］，若4维系统(2)还存在一个独立于Hamilton函数H(x)的首次积分I(x)，则它的解均在H(x)和I(x)确定的水平集上，而这个水平集是紧致的(H(x)的水平集拓扑等价于3维球面)．故由完全可积性定理知，该水平集拓扑等价于2维不变环面，其上若存在周期解，则必属于定理1中那两族之一．

另一方面，对充分小的a23≠0，系统(2)在式(5)和式(6)成立的条件下至少有3族非退化的周期轨道．因此，可得定理3．

定理3 对充分小的a23≠0，系统(2)在Liouville意义下是不可积的．

下面用Lyapunov指数来数值论证系统(2)是否出现Hamilton混沌．

Lyapunov指数是反映一个动力系统是否存在混沌的主要工具［12］．若所考虑的动力系统存在正的Lyapunov指数，则可认为系统是混沌的．

对于系统(2)，若取参数a12=a23=a34=1，b1=b3=-1，b2=b4=1，则用数学软件Maple计算该系统的最大Lyapunov指数，结果如图1所示．

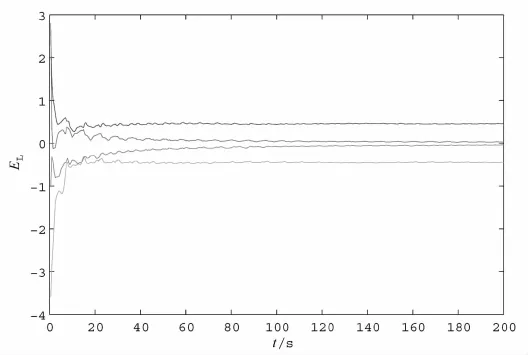
图1 Lyaounov指数

从图1可看到，系统(2)的4个Lyapunov指数中有2个为0，另外2个Lyapunov指数为±0．445．因此，此系统是混沌的．

［1］Hofbauer J，Sigmund K．Evolutionary games and population dynamics［M］．Cambridge:Cambridge University Press，1998．

［2］Xia Yonghui．New results on the global asymptotic stability of a Lotka-Volterra system［J］．Appl Math Comput，2011，36(1/2):117-128．

［3］Svirezhev Y M．Nonlinearities in mathematical ecology:Phenomena and models:Would we live in Volterra's world?［J］．Ecological Modelling，2008，216(2):89-101．

［4］Upadhyay R K．Observability of chaos and cycles in ecological systems:Lessons from predator-prey models［J］．International Journal of Bifurcation and Chaos，2009，19(10):3169-3234．

［5］Duarte P，Fernandes R L，Oliva W M．Dynamics of the attractor in the Lotka-Volterra equations［J］．Journal of Differential Equations，1998，149(1):143-169．

［6］Zhao Xiaohua，Luo Jigui．Classification and dynamics of stably dissipative Lotka-Volterra systems［J］．International Journal of Nonlinear Mechanics，2010，45(6):603-607．

［7］赵晓华，吴红颖．保守型Lotka-Volterra系统的Hamilton结构与周期解［J］．浙江师范大学学报:自然科学版，2007，30(3):246-250．

［8］Picard G，Johnstone T W．Instabillity cascades，Lotka-Volterra population equations，and Hamilton chaos［J］．Physical Review Letters，1982，48(23):1610-1613．

［9］李继彬，赵晓华，刘正荣．广义哈密尔顿系统理论及其应用［M］．2版．北京:科学出版社，2007．

［10］Meyer K R，Hall G R，Offin D．Introduction to Hamiltonian dynamical systems and the N-body problem［M］．2nd ed．New York:Springer，2009．

［11］Milnor J．Morse theory［M］．New Jersey:Princeton University Press，1969．

［12］Ott E．Chaos in dynamical systems［M］．2nd ed．Cambridge:Cambridge University Press，2002．