拓扑空间关于子基的分离性

刘德金

(德州学院数学系,山东德州 253023)

拓扑空间关于子基的分离性

刘德金

(德州学院数学系,山东德州 253023)

在粗糙集理论研究中,覆盖方法的应用越来越受到重视,其中拓扑空间的子集关于子基的内部和闭包两个概念尤为重要.本文在由它们导入的关于子基的开集,闭集的基础上,给出了拓扑空间关于子基的分离性概念,并研究它们的性质,得到分离性公理定义的一般拓扑空间的进一步分类.

子基;β开集;关于子基的正则空间;关于子基的正规空间;关于子基的完全正则空间

1982年波兰人Pawlak在文[1]建立的粗糙集理论为数据挖掘和知识发现领域提供了不同于常规数据库方法的一种有效而新颖的理论,在理论界产生了很大影响,使得粗糙集理论的实际应用与理论探讨成为当前计算机科学中的一个热点问题.粗糙集的研究已有很多出色的工作,文[2-6]研究了粗糙集的代数结构;文[7-8]研究了粗糙集的可测结构;文[9-11]研究了粗糙集与拓扑空间的关系.文[12]将粗糙集理论推广到覆盖广义粗糙集理论,随后吸引了不少学者对覆盖广义粗糙集理论进行了深入的研究[13-18].为了使粗糙集理论和覆盖广义粗糙集理论中的下近似集和上近似集都能分别地对应于某一拓扑空间子集的某种内部和闭包,文[17]定义了拓扑空间的子集关于子基的内部和闭包;文[18]研究了拓扑空间的子集关于子基的连通性概念.本文在文[17]引入的拓扑空间关于子基的开集、闭集的基础上,给出了关于子基的分离性概念,并研究它的性质,得到一般拓扑学中分离性公理所定义空间的进一步分类.

文中关于子基的内部,闭包,开集,闭集,邻域等概念均见文[17-18],Ti空间(i=0,1,2,3,4),正则空间,完全正则空间,正规空间等概念均见文[19],在此不赘述.

设X为非空集合,给定X上的拓扑T,如果β是T的子基,则该拓扑空间记为(X,T,β).

并且如果x的β邻域是β开集,则称其为β开邻域.X的子集A的补集记为～A.

定义1 设(X,T,β)是拓扑空间,若x,y∈X,x≠y,x,y中必有一点存在一个β开邻域不包含另一点,则称该空间为关于子基的T0空间,简称β-T0空间.

因为β开集是开集[18],所以可知,β-T0空间是T0空间.

定理1 (X,T,β)是β-T0空间的充分必要条件是X中任意两个不同的单点集有不同的β闭包.即若x,y∈X,x≠y,则Cβ({x})≠Cβ({y}).

证充分性.设x,y∈X,x≠y,若Cβ({x})≠Cβ({y}),则或者Cβ({x})Cβ({y})≠Ø,或者Cβ({y})Cβ({x})≠Ø.当Cβ({x})Cβ({y})≠Ø时,必有x∉Cβ({y})(因为若x∈Cβ({y}),则{x}⊂Cβ({y}),从而由[18]知Cβ({x})⊂Cβ({y}),于是Cβ({x})Cβ({y})=Ø).这推出x有一个不包含y的β开邻域～Cβ({y}).同理,当Cβ({y})Cβ({x})≠Ø时,y有一个不包含x的β开邻域～Cβ({x}).故X是β-T0空间.

必要性.设X是β-T0空间.若x,y∈X,x≠y,则或者x有一个β开邻域U使得y∉U,或者y有一个β开邻域V使得x∉V.若属于前一种情况,则U∩{y}=Ø,所以x∉Cβ({y}),所以Cβ({x})≠Cβ({y});若属于后一种情况,则V∩{x}=Ø,所以y∉Cβ({x}),所以Cβ({y})≠Cβ({x}).

定义2 设(X,T,β)是拓扑空间,若X中任意两个不同的点中每一个点都有一个β开邻域不包含另一点,则称该空间为关于子基的T1空间,简称β-T1空间.

显然,β-T1空间是β-T0空间,β-T1空间是T1空间.

例1 X={a,b,c,d},β={{a,b},{a,c},{c},{b,d}}.

β开集:Ø,{a,b},{a,c},{c},{b,d},{a,b,c},{b,c,d},{a,b,d},{a,b,c,d}.

易知X是β-T0空间.因为含d的β开集一定含b,所以X不是β-T1空间.

定理2 (X,T,β)是β-T1空间的充分必要条件是X中的每个单点集是β闭集.

证必要性.设X是β-T1空间,x∈X,则y∈X,y≠x,y有一个β开邻域V使得x∉V,即V∩{x}=Ø,所以y∉Cβ({x}),所以Cβ({x})={x}.由文[17]定理3.6知{x}是β闭集.

充分性.设x,y∈X,x≠y,由条件{x},{y}都是β闭集,所以～{x},～{y}分别是包含y和x的β开集,～{x}不含x,～{y}不含y.所以X是β-T1空间.

定义3 设(X,T,β)是拓扑空间,若X中任意两个不同的点各自都有一个β开邻域使得这两个β开邻域互不相交,则称该空间为关于子基的T2空间,简称β-T2空间.

由定义知,β-T2空间是β-T1空间,β-T2空间是T2空间.

例2(非β-T2空间的β-T1空间) 设X是一个包含无限多个点的有限补拓扑空间,则比X仅少一个点的所有子集构成的集族是X的一个子基,即β={X{x}|x∈X}是X的一个子基,因此X的每个单点集是β闭集,所以由定理2,X是一个β-T1空间.显然任意两个非空β开集都有非空的交,所以X不是一个β-T2空间.

注 若X是β-T1空间,点x∈X是X的子集A的β凝聚点[17],则x的β开邻域U中不一定含A的无限多个点.如在本例中,A={a,b},a,b∈X,则x∈X,x≠a,b,x是A的一个β凝聚点,但x的任何β邻域U最多含A的两个点.这与T1空间中子集A与其凝聚点的关系情况不同.

例3 实数空间R,子基β={(∞,b)|b∈R}∪{(a,+∞)|a∈R}.对任意两点x,y∈R,x≠y,不妨设x＜y,取z=(x+y),则(∞,z),(z,+∞)是分别含x和y的两个不交的β开邻域,所以实数空间R是β-T2空间.

定义4 设{xi}i∈Z+是拓扑空间(X,T,β)中的一个序列[19],x∈X,如果对于x的每个β开邻域U,存在M∈Z+使得当i＞M时,xi∈U,则称点x是序列{xi}i∈Z+的一个β极限点(或β极限),也称序列{xi}i∈Z+β收敛于x,记作xi=βx,或xi→βx(i→∞).如果序列至少有一个β极限,则称这个序列是β收敛序列.

定义5[18]设(X,T1,β)与(Y,T2,α)是两个拓扑空间,f∶X→Y.如果Y的每个α开集U的原像f-1(U)是X的β开集,则称f为(β,α)连续映射.

因为Y中每个开集U是Y中子基α的有限个元素交的任意并,所以f-1(U)是α的有限个元素原象的交的任意并,而α的每个元素的原象是X的β开集,从而是开集,所以f-1(U)是X的开集,所以若f为(β,α)连续映射,则f为连续映射.

定理3 设(X,T1,β)与(Y,T2,α)是两个拓扑空间,f∶X→Y是(β,α)连续映射,则{xi}i∈Z+β收敛于x蕴含着Y中序列{f(xi)}i∈Z+α收敛于f(x).

证设V是Y的包含f(x)的任意α开集,因为f∶X→Y是(β,α)连续映射,所以f-1(V)是X的一个β开集,且x∈f-1(V),因为{xi}i∈Z+β收敛于x,所以对于f-1(V)存在M,使得当i＞M时xi∈f-1(V),从而f(xi)∈V.即对Y中包含f(x)的任意α开集V,存在M,使得当i＞M时,f(xi)∈V.所以Y中序列{f(xi)}i∈Z+α收敛于f(x).

定理4 β-T2空间中的任何一个β收敛序列只有一个β极限点.

证设{xi}i∈Z+是拓扑空间(X,T,β)中的一个序列,并且xi=βx,xi=βy.若x≠y,因为X是β-T2空间,则存在β开集U,V使x∈U,y∈V,且U∩V=Ø.因为xi=βx,所以对U,存在M1＞0使得i＞M1时,xi∈U;又因为xi=βy,所以对V,存在M2＞0使得i＞M2时,xi∈V.取N=max{M1,M2},则当i＞N时,xi∈U,xi∈V,这与U∩V=Ø矛盾.

定义6 设(X,T,β)是拓扑空间,如果对任意的x∈X和闭集B,x∉B,存在β开邻域U,V,使得x∈U,B⊂V,且U∩V=Ø,则称X是关于子基的正则空间,简称β正则空间.

显然,β正则空间是正则空间.

定理5 设(X,T,β)是拓扑空间,则(X,T,β)是β正则空间的充分必要条件是对每个x∈X和x的开邻域U,存在x的β开邻域W,使得x∈W⊂Cβ(W)⊂U.

证必要性.设U是开集,x∈U,则～U是闭集,且x∉～U.由β正则空间的定义,存在β开邻域W,V,使得x∈W,～U⊂V,且W∩V=Ø,所以W⊂～V⊂U.因V是β开集,所以～V是β闭集,即Cβ(～V)=～V,而W⊂Cβ(W)⊂Cβ(～V)=～V⊂U,所以x∈W⊂Cβ(W)⊂U.

充分性.设x∈X,B是X的闭集,x∉B,所以x∈～B(X的开集),由条件存在β开集W使x∈W⊂Cβ(W)⊂～B,所以B⊂～Cβ(W),～Cβ(W)是β开集,且～Cβ(W)∩W=Ø,即存在β开集W和～Cβ(W)使x∈W,B⊂～Cβ(W),且～Cβ(W)∩W=Ø,所以X是β正则空间.

定义7 设(X,T,β)是拓扑空间,如果对X的任意两个不交的闭集A,B,存在β开邻域U,V,使得A⊂U,B⊂V,且U∩V=Ø,则称X是关于子基的正规空间,简称β正规空间.

易知,β正规空间是正规空间.例2,例3所给空间不是β正则空间,也不是β正规空间.

例4 X={1,2,3},T={Ø,{1},{2,3},{1,2,3}},β={{1},{2,3}},显然β开集族等于T,可知X是β正则,β正规空间.但X不是β-T0空间,从而不是β-T1,β-T2空间.

定理6 设(X,T,β)是拓扑空间,则(X,T,β)是β正规空间的充分必要条件是对X的任何一个闭集A和A的任何开邻域V,存在β开集U,使得A⊂U⊂Cβ(U)⊂V.

证必要性.设A是X的闭集,V是开集,A⊂V,则～V是闭集,且～V∩A=Ø.因为X是β正规空间,所以存在β开邻域U,W使得A⊂U,～V⊂W,且U∩W=Ø,所以U⊂～W⊂V.因为W是β开集,所以～W是β闭集,即Cβ(～W)=～W,所以A⊂U⊂Cβ(U)⊂Cβ(～W)=～W⊂V.

充分性.设A,B是X的任意两个不交的闭集,即A∩B=Ø,则A⊂～B,～B是开集.由条件存在A的β开集U使A⊂U⊂Cβ(U)⊂～B.取V=～Cβ(U),则V是β开集,且B⊂V,U∩V=Ø.所以X是β正规空间.

定理7 设(X,T1)与(Y,T2)同胚,同胚映射是h.若β是T1的子基,则h(β)={h(A)|A∈β}是T2的一个子基;反之若α是T2的子基,则h-1(α)={h-1(B)|B∈α}是T1的一个子基.

证因为h是同胚映射,所以只证:若β是T1的子基,则h(β)是T2的一个子基.

设B1={S1∩S2∩…∩Sn|Si∈β,1≤i≤n,n∈Z+},则B1⊂T1,B1是T1的基.记B2={T1∩T2∩…∩Tn|Ti∈h(β),1≤i≤n,n∈Z+},则B2⊂T2.若证h(β)是T2的一个子基,只需证B2是T2的一个基.

定理8 设(X,T1)与(Y,T2)同胚,同胚映射是h,若β是T1的子基,则若U是X的β开集,则h(U)是Y的h(β)开集;反之,若γ是T2的子基,V是Y的γ开集,则h-1(V)是X的h-1(γ)开集.

证由定理7和一一映射保并运算以及关于子基的开集的定义可得.

注 由这两个定理可见,两个拓扑空间同胚,则它们的子基对应子基,关于子基的开集对应于关于相应子基的开集.

定理9 设(X,T,β)是拓扑空间,[a,b]是R的闭区间,α是[a,b]的子基.则X是β正规空间的充分必要条件是对X的任意两个不交的闭集A和B,存在一个(β,α)连续映射f∶X→[a,b],使得x∈A时f(x)=a,x∈B时f(x)=b.

证 由于[a,b]同胚于[0,1],所以由上面的注可知对[a,b]=[0,1]证明即可.

我们知道S={(∞,b)|b∈R}∪{(a,+∞)|a∈R}是实数空间R的一个子基,则

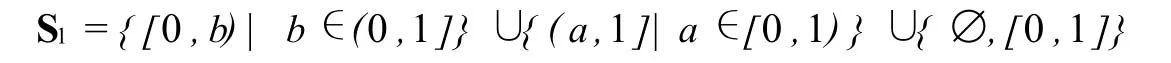
是[0,1]的一个子基,其实易知α={[0,b)|b∈(0,1]}∪{(a,1]|a∈[0,1)}仍是[0,1]的一个子基.

必要性.设X是β正规空间,A,B是X中两个不交的闭集,则存在β开集U,V,使A⊂U,B⊂V, U∩V=Ø.从而可知A∩Cβ(B)=Ø.

令QI=Q∩[0,1],即QI是[0,1]中的全体有理数构成的集合.由于QI是一个无限的可数集,故有一个一一映射r:Z+→QI,因此可记QI={r(1),r(2),r(3),…},不妨设r(1)=1和r(2)=0.我们将每一个有理数r(n)∈QI,对应A的一个β开邻域Ur(n)使得满足条件:

(i)Ur(1)=～Cβ(B);

(ii)如果r(n)＜r(m),则Cβ(Ur(n))⊂Ur(m).

现在按归纳方式定义A的诸β开邻域Ur(n)如下:

首先令U1=Ur(1)=～Cβ(B).因A∩Cβ(B)=Ø,故A⊂～Cβ(B)=Ur(1),据定理6,任意选取U0=Ur(2)为A的一个β开邻域,使Cβ(Ur(2))⊂Ur(1),此时易见Ur(1)和Ur(2)满足以上条件(i),(ii).

对于n＞2,假定A的诸β开邻域Ur(1),Ur(2),…,Ur(n-1)已经定义,并且满足上述条件(i),(ii),下面定义Ur(n):记在诸实数r(1),r(2),…,r(n1)中小于r(n)的各数中最大的一个为s,大于r(n)的各数中最小的一个为b.据定理6,选取Ur(n)为Cβ(Us)的一个β开邻域使得Cβ(Ur(n))⊂Ub.

从Ur(n)的取法可见,A的诸β开邻域Ur(1),Ur(2),…,Ur(n-1),Ur(n)仍然满足上述条件(i),(ii).

根据归纳原则,A的诸β开邻域Ur(1),Ur(2),…,Ur(n)已经全部定义且满足条件(i),(ii).

定义映射f:X→[0,1]使得对任何x∈X,

显然,如果x∈A,则由于x∈U0(=Ur(2)),所以f(x)=0.如果x∈B,因为B⊂Cβ(B),则根据f的定义便有f(x)=1.

下面证f是(β,α)连续的.

要验证f是(β,α)连续的,根据逆映射保并运算和β开集的任意并仍是β开集[18],只需证明α中每个元素的原像是X中的β开集即可.

(i)对任何a∈[0,1),f-1((a,1])是X中的β开集.

定义8 设(X,T,β)是拓扑空间,α是R的子空间[0,1]的子基.如果对任意的x∈X和X的任一闭集A,x∉A,存在(β,α)连续映射f∶X→[0,1],使得f(x)=0,以及对每个y∈A,f(y)=1,则称(X,T,β)是关于子基的完全正则空间,简称β完全正则空间.

易知,β完全正则空间是完全正则空间.

定理10 β完全正则空间是β正则空间.

证设(X,T,β)是β完全正则空间,x∈X,A⊂X,A是闭集,x∉A.由条件存在(β,α)连续映射f∶X→[0,1],使得f(x)=0,以及对每个y∈A,f(y)=1.因为[0,1]的子基是

定理11 每个β正则且β正规的空间一定是β完全正则空间.

证设(X,T,β)是β正则且β正规的空间.对于任意的x∈X,设A是X的一个闭集,且x∉A,所以x∈～A,～A是开集.因X是β正则空间,所以对x和x的开邻域～A,存在x的β开集W使x∈W⊂Cβ(W)⊂～A,所以Cβ(W)∩A=Ø,因β闭集是闭集.所以Cβ(W),A是X中的两个无交的闭集.因X是β正规空间,所以由定理9,存在(β,α)连续映射f:X→[0,1],使得y∈Cβ(W)时,f(y)=0,y∈A时,f(y)=1.因为x∈Cβ(W),所以f(x)=0.故X是β完全正则空间.

定义9 β正则且β-T1的拓扑空间叫做β-T3空间;β正规且β-T1的拓扑空间叫做β-T4空间.

因β-T1空间中的每一个单点集是β闭集,而β闭集是闭集,所以β-T4空间一定是β-T3空间,β-T3空间一定是β-T2空间.并且β-T4空间是T4空间,β-T3空间是T3空间.

定义10 设(X,T,β)是拓扑空间,(Y,T|Y,β|Y)是其子空间.如果Y是β|Y正则(β|Y正规,β|Y完全正则,β|Y-Ti)空间,则称Y是X的β正则(β正规,β完全正则,β-Ti)子空间,或称Y作为X的子空间也是β正则(β正规,β完全正则,β-Ti)空间.其中0≤i≤4.

定理12 β-T4空间(X,T,β)中任何一个β连通子集[18]如果包含着多于一个点,则它一定是一个不可数集.

证设C是β-T4空间(X,T,β)中一个β连通子集,如果C包含不只一个点,任意选取x,y∈C, x≠y.对于β-T4空间X中的两个不交的闭集{x},{y}应用定理9,则存在(β,α)连续映射f∶X→[0,1],使得f(x)=0和f(y)=1.由于C是一个β连通子集,由文[18]定理1.17知f(C)也是[0,1]的α连通子集,由文[18]定理1.18可知f(C)是[0,1]的区间.又0,1∈f(C),所以f(C)=[0,1].因为[0,1]是不可数集,所以C也是不可数集.

定理13 若(X,T,β)是β正则空间,则它的每个子空间是β正则子空间.

证首先,X的β开集与Y的交是Y的β|Y开集.事实上由文[18]知,CβY(A)=Cβ(A)∩Y,所以iβY(A)=～CβY(～A)=～Cβ(～A)∩Y=iβ(A)∩Y,从而可知X的β开集U与Y的交U∩Y是Y的β |Y开集.

设(X,T,β)是β正则空间,Y⊂X.任取y∈Y和Y的闭子集B,y∉B,则存在X的闭子集A使得B=A∩Y,且y∉A.由于X是β正则空间,所以存在X的两个β开集U,V使y∈U,A⊂V,且U∩V =Ø.于是U∩Y,V∩Y是Y的β|Y开集,且(U∩Y)∩(V∩Y)=Ø,y∈U∩Y,B⊂V∩Y.所以Y是β|Y正则的,即Y是X的β正则子空间.

定理14 若(X,T,β)是β完全正则空间,则它的每个子空间也是β完全正则空间.

证设Y⊂X,任取y∈Y和Y的闭子集B,y∉B,则存在X的闭子集A使得B=A∩Y,且y∉A.因为X是β完全正则空间,所以存在(β,α)连续映射f∶X→[0,1],使得f(y)=0,x∈A时f(x)=1.于是f|Y是(β|Y,α)连续映射.f|Y∶Y→[0,1]使得f|Y(y)=f(y)=0,x∈B时,x∈A,f|Y(x)=f(x) =1.所以Y是β|Y完全正则的.即Y作为X的子空间是β完全正则空间.

定理15 若(X,T,β)是β正规空间,则它的每个闭子空间也是β正规空间.

证 设(X,T,β)是β正规空间,Y是X的闭子集,若A,B是Y的两个不交的闭子集,则A,B也是X的两个不交的闭子集.因X是β正规空间,所以存在X的两个β开集U,V使A⊂U,B⊂V,且U∩V =Ø.于是令U1=U∩Y,V1=V∩Y,则U1,V1是Y的两个β|Y开集,且A⊂U1,B⊂V1,U1∩V1=Ø,所以Y是β|Y正规空间,即Y作为X的子空间是β正规空间.

可以证明,β-Ti空间的子空间是β-Ti空间,其中0≤i≤3.β-T4空间的闭子空间是β-Ti空间.

定理16 设(X,T1)与(Y,T2)同胚,同胚映射是h∶X→Y.若β是T1的子基,X是β-T0(β-T1,β-T2)空间,则Y是h(β)-T0(h(β)-T1,h(β)-T2)空间;反之,若γ是T2的子基,Y是γ-T0(γ-T1,γ-T2)空间,则X是h-1(γ)-T0(h-1(γ)-T1,h-1(γ)-T2)空间.

证仅证其中之一:若X是β-T1空间,则Y是h(β)-T1空间,其它几个结论类似可证.

任给y1,y2∈Y,y1≠y2,则存在x1,x2∈X使得h(x1)=y1,h(x2)=y2,且x1≠x2.因为X是β-T1空间,所以存在X的β开集U1,U2,使得x1∈U1,x2∉U1;x2∈U2,x1∉U2.由定理8,h(U1), h(U2)是Y的h(β)开集,且因为x1∈U1,x2∉U1,所以y1=h(x1)∈h(U1),y2=h(x2)∉h(U1);因为x2∈U2,x1∉U2,所以y1=h(x1)∉h(U2),y2=h(x2)∈h(U2).即在Y中,存在两个h(β)开集h(U1), h(U2)分别包含y1,y2,而h(U1)不含y2,h(U2)不含y1.故Y是h(β)-T1空间.

定理17 设(X,T1)与(Y,T2)同胚,同胚映射是h:X→Y.若β是T1的子基,X是β正则空间,则Y是h(β)正则空间;反之,若γ是T2的子基,Y是γ正则空间,则X是h-1(γ)正则空间.

证y∈Y和Y的闭子集B,y∉B,则x=h-1(y)∈X,A=h-1(B)是X的闭集,且x∉A.因为X是β正则空间,所以存在β开集U,V,使得x∈U,A⊂V,且U∩V=Ø.于是由定理8知h(U),h(V)是Y的h(β)开集,且y=h(x)∈h(U),B=h(A)⊂h(V),h(U)∩h(V)=Ø.所以Y是h(β)正则空间.反之,类似可证.

定理18 设(X,T1)与(Y,T2)同胚,同胚映射是h∶X→Y.若β是T1的子基,X是β完全正则空间,则Y是h(β)完全正则空间;反之,若γ是T2的子基,Y是γ完全正则空间,则X是h-1(γ)完全正则空间.

证任取y∈Y和Y的闭子集B,y∉B,则x=h-1(y)∈X,A=h-1(B)是X的闭集,且x∉A,因为X是β完全正则空间,所以存在(β,α)连续映射f∶X→[0,1],使得f(x)=0,x∈A时f(x)=1.取g=f◦h-1∶Y→[0,1],则g是(h(β),α)连续的,且g(y)=(f◦h-1)(y)=f[h-1(y)]=f(x)=0, z∈B时,x=h-1(z)∈A,g(z)=(f◦h-1)(z)=f[h-1(z)]=f(x)=1.所以Y是h(β)完全正则空间.

反之,任取x∈X和X的闭子集A,x∉A.因h是同胚映射,所以y=h(x)∈Y,h(A)是Y的闭集, y∉h(A).因为Y是γ完全正则空间,所以存在(γ,α)连续映射f∶Y→[0,1],使得f(y)=0,z∈h(A)时,f(z)=1.取g=f◦h:X→[0,1],则g是(h-1(γ),α)连续映射,且g(x)=(f◦h)(x)=f[h(x)] =f(y)=0,y∈A时,z=h(y)∈h(A),g(y)=(f◦h)(y)=f[h(y)]=f(z)=1.所以X是h-1(γ)完全正则空间.

定理19 设(X,T1)与(Y,T2)同胚,同胚映射是h:X→Y.若β是T1的子基,X是β正规空间,则Y是h(β)正规空间;反之,若γ是T2的子基,Y是γ正规空间,则X是h-1(γ)正规空间.

证因为h是同胚映射,所以只需证其中一句话,不妨证第二句话.即设γ是T2的子基,Y是γ正规空间,下面证X是h-1(γ)正规空间.

由定理7,h-1(γ)是X的子基.任取X的两个不交的闭子集A,B,则A1=h(A),B1=h(B)是Y的两个不交的闭子集.因Y是γ正规空间,所以存在Y的两个γ开集U1,V1使A1⊂U1,B1⊂V1且U1∩V1=Ø,则U=h-1(U1),V=h-1(V1)是X的h-1(γ)开集,h-1(A1)⊂U,h-1(B1)⊂V,且U∩V=Ø,即A=h-1(A1)⊂U,B=h-1(B1)⊂V,且U∩V=Ø,所以X是h-1(γ)正规空间.

由以上几定理可得:

定理20 设(X,T1)与(Y,T2)同胚,同胚映射是h:X→Y.若β是T1的子基,X是β-T3(β-T4)空间,则Y是h(β)-T3(h(β)-T4)空间;反之,若γ是T2的子基,Y是γ-T3(γ-T4)空间,则X是h-1(γ)-T3(h-1(γ)-T4)空间.

定理16—20说明,在同胚映射下,满足定义1—3,6—9的关于子基分离性的空间一定变到关于某一子基的同种分离性的空间.例如,关于子基的正则空间在同胚映射下一定变到关于一个子基的正则空间等.不满足关于子基分离性的空间在同胚映射下一定不是关于子基分离性的空间.

[1] Pawlak Z.Rough sets[J].International Journal of Computer and Information Sinence,1982,11：341-356.

[2] Biswas R,Nanda S.Rough groups and rough subgroups[J].Bull.Polish Acad.Sci.Math.,1994,42：251-254.

[3] Iwinski J.Algebraic approach to rough sets[J].Bull.Polish Acad.Sci.Math.,1987,35：673-683.

[4] Kuioki N,Wang P P.The lower and upper approximations in fuzzy group[J].Inform.Sci.,1996,90：203-220.

[5] Kuioki N.Rough ideals in semigroups[J].Inform.Sci.,1977,100：139-163.

[6] 祝峰,何华灿.粗集的公理化[J].计算机学报,2000,23：330-333.

[7] 张仕念,刘文奇.可测空间与Pawlak代数[J].模糊系统与数学,2001,15：40-43.

[8] 于剑,程乾生.粗集与不可测集[J].科学通报,2000,45：686-688.

[9] Yao Y Y.Relationl interpretations of neighborhood operators and rough set approximation operators[J].Inform. sci.,4988,111：239-259.

[10] 陈德刚,张文修.粗糙集与拓扑空间[J].西安交通大学学报,2001,35：1314-1315.

[11] 李进金.覆盖广义粗糙集理论中的拓扑方法[J].模式识别与人工智能,2004,17(1)：7-10.

[12] Zakowski W.Approximations in the space(U,R)[J].Demonstratio Matheznatica,1983,16：761-769.

[13] Bryniaski E.acalculus of rough sets of the first order[J].Bulletin of the Polish Academy of Sciences,1989, 37(16)：71-77.

[14] Bonikowski Z,Bryniarski E,Wybraniec-Skardowska U.Extensions and intentions in the rough set theory[J]. Information Science,1998,107：149-167.

[15] Pomykala J A.Approximation operations in approximation space[J].Bulletion of the Polish Academy of Science, 1987,35(9-10)：653-662.

[16] 祝峰,王飞跃.关于覆盖广义粗集的一些基本结果[J].模式识别与人工智能,2002,15(1)：6-12.

[17] 李进金.由子基生成的内部算子和闭包算子[J].数学进展,2006,35(4)：478-484.

[18] 李进金.关于子基的连通性[J].数学进展,2007,36(4)：421-428.

[19] 熊金诚.点集拓扑讲义[M].3版.北京：高等教育出版社,2003.

The Separateness Relative to a Subbase for the Topology

L IU De-jin

(Dept.of Math.,Dezhou University,Dezhou,Shandong 253023,China)

Covering methods are widely used in rough set theory.The interior and the closure of a subset relative to a subbase for the topology are introduced to study the relationships between the rough sets and the topological space.We introduce and study Separateness relative to a subbase for the topology on the basis of open set and closed set relative to a subbase,and some properties are also discussed.We also obtain the further classification for general topological space defined by separation axiom.

subbase;theβopen set;the regular space relative to a subbase;the normal space relative to a subbase; the completely regular space relative to a subbase

O189.1;TP18

A

1672-1454(2011)03-0059-07

2008-08-04