有界模糊数的比较与排序
高德宝
(黑龙江八一农垦大学 文理学院,黑龙江 大庆 163319)
在用模糊数及模糊关系构建的数学优化模型中,对于可行域上的任一点,通过模糊关系运算得到的目标值均是模糊数。这样就存在哪个模糊数较优的问题,依据模糊数的优劣程度进行比较或排序的问题称之为模糊数的排序问题。在模糊优化与决策中,模糊数的比较与排序问题是基本问题。迄今为止,国内外学者相继提出了多种方法[1-6]。但没有一种方法能得到普及,它们均各有优缺点,各有适用范围。
定义 1[7]设A是实数域R上的正规模糊集,且对∀λ∈ [0,1],Aλ均为一闭区间,则称A为一个模糊数。若∀λ∈ (0,1],Aλ有界,则称A为有界模糊数。
定理 1[7]A为有界模糊数的充分必要条件是存在闭区间[al,ar],使得
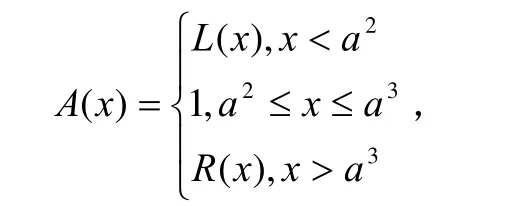
其中L(x)为增函数,右连续,0 ≤L(x ) < 1,且R (x)为减函数,左连续, 0≤R(x)< 1,且
易知L(x)与R(x)均有逆函数,设其分别为L-1(x),R-1(x),则L-1(x),R-1(x)仍是右,左连续且仍是增函数与减函数。
本文所涉及的模糊数 Ai(i = 1,2, … ,n)的隶属函数为:

1 模糊数的排序方法
定义2[8]设E是一个非空集, xy∈E∀, ,给定一个实数ρ(x,y)与之对应,若ρ(x,y)满足如下条件:
(1) ρ( x,y) ≥0,且 ρ( x,y)=0当且仅当x=y;
(2) ρ( x, y)= ρ(y,x);
(3) ρ(x,y)≤ ρ(x,z)+ρ(z,y),( z∈E)。
则称ρ(x,y)是两点x,y之间的距离。
定义3对任意的模糊数 A1,A2,称

为模糊数 A1与A2之间的距离。
易知定义3满足定义2中的所有条件。
距离的几何意义:如图 1所示, A1,A2的距离是指在A( x)=1与A(x)=0之间,L1(x),L2(x)所围面积的p次幂与 R1(x),R2(x)所围面积的p次幂之和的平均值之后开p次方。当 A1,A2为实数时,即它等同于实数的距离公式。

图1 A1与A2之间的距离
定义4[2]设A为一模糊数,若x<0时,A(x)=0,则称A是正模糊数;若x>0时,A(x)=0,则称A为负模糊数;若存在 x1x2< 0,使得 A(x1)A( x2) >0,则称A是变号模糊数。
定义 5若A为正模糊数,称 wA= d(A,0)为A的排序指标;若A为负模糊数,称 wA=- d(A,0)为A的排序指标;若0∈ (a1,a4),取 A= Al∨ Ar,其中

定义6若 wA1< wA2,记作A1< A2,读作A1小于A2;若wA1= wA2,记作 A1=A2,读作A1等于A2。
若要对若干个有界模糊数 Ai(i = 1,2,… ) 进行排序,需先算出对应的 d(Ai,0)(i = 1,2,… ) ,然后再根据对应的wAi的大小对 Ai进行排序。
2 排序效果分析
定理1设 A1,A2为两个LR模糊数。,则有 A1≤A2。
证明分三种情形。
(1)A1(x),A2(x)均为正模糊数
由于A1(x),A2(x)均为凸函数,所以当时有

故A1≤A2。
(2) A1,A2均为负模糊数
综上所述,原命题成立。
特别地,当A1为实数或A2为实数,仍有 A1≤A2。
推论若A2为正模糊数,则 A1≤ A1+ A2;若A2为负模糊数,则 A1+ A2≤ A1。
这些结果与人们的直觉是相符的并且不悖逆于实数的自然序关系。在一定程度上说明了此排序方法的有效性。
本文的排序方法具有以下几方面的合理性:
性质 1对任意的有界模糊数A1与A2, A1≤A2与A2≤ A1至少有一个成立。
性质2对任意的有界模糊数若,则A1≤A2。
性质3对任意的A1(x),A2(x),A3(x),若 A1≤ A2且A2≤ A3,则 A1≤ A3。
性质 4若在集合{ A1, A2}上有 A1≤ A2,则在集合{A1,A2,A3}上也有 A1≤A2。
性质5对任意的A1(x),A2(x),若有 A1≤ A2,则当r为正实数时,有 rA1≤ rA2。
证明性质1~4由序的定义易知,下证性质5。
由定义3知,d (r A,0)= rd(A,0)。从而可知 wrA1=rwA1,wrA2=rwA2。由 A1≤ A2知, wA1≤ wA2。
故rwA1≤ rwA2,从而 rA1≤ rA2。
3 实例分析
下面我们对具有代表性的五组模糊数的排序问题[8]进行分析,图 2(a)~图 2(e)分别对这五组具有代表性的模糊数进行了描述。
在定义3中,我们仅取p=2时。
对于图 2(a)中所示的三个模糊数 A1=(0.4,0.5,0.5,1),A2=(0.4,0.7,0.7,1), A3=(0.4,0.9,0.9,1),易知 A1,A2,A3的支撑区间都相同且它们的峰值区间都为一个点,故其峰值区间越靠右表示的数值越大,即 A1< A2< A3。用本文方法可得:
wA1= 0.6185, wA2= 0.7159, wA3= 0.8139。由此可得: A1< A2< A3。
对于图2(b)中所示的两个模糊数 A1= (0. 2,0.5,0.5,0.8) ,A2= (0.4,0.5,0.5,0.6)易知A1与A2的峰值区间相同,故其支撑区间越小越精确,即 A2< A1。用本文方法可得:
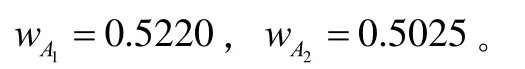
由此可得: A2< A1。

图2 五组模糊数的排序问题
对于图 2(c)所示的三个模糊数 A1= (0.5,0.7,0.7,0.9),A2= (0.3,0.4,0,7,0.9), A3=(0.3,0.4,0,7,0.9),易知A1与A2的峰值区间相同,故其支撑区间越小越精确。即 A2< A1。根据性质4,待序范围扩大后,也应有 A2< A1。A2与A3的支撑区间相同,峰值区间越往右越大,故 A2< A3。用本文方法可得
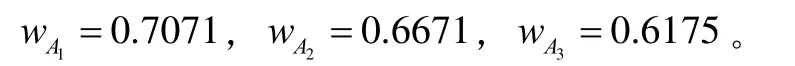
由此可得: A3< A2< A1。
对于图 2(d)中的三个模糊数 A1= (0.3,0.5,0.8,0.9),A2=(0.3,0.5,0.5,0.9)与A3=(0.3,0.5,0.5,0.7),易知A1与A2的支撑区间相同,峰值区间越往右越大,即 A2< A1。根据性质4,待序范围扩大后,也应有 A2< A1,且A2与A3的峰值区间相同都为同一个点,故支撑区间越大越精确。即A3< A2,所以 A3< A2< A1。用本文方法可得

由此可得: A3< A2< A1。
对于图 2(e)中的两个模糊数 A1= (0.3,0.3,0.3,1),A2= (0.1,0.7,0.7,0.8),仅仅从对数值描述的精确程度方面看,两者是相同的,且由 [0 .1,0.8]< [0.3,1]可得 A.1> A2;另一方面,由于 A1的支撑区间小于A2的支撑区间,故有A1<A2。综合两方面考虑就很难确定两者的优越程度,用本文方法可得

虽然能得出 A1<A2,但我们也能看到 wA1与 wA2相差无几,这符合上面的分析结果。
4 结论
给出了度量模糊数间距离的一种新方法的基础上,提出了模糊数的排序指标,进而能够确定模糊数之间的序关系。文中从理论分析与实例分析两个方面说明排序方法的效性与实际可行性。

