改进的DNA遗传算法在指派问题中的应用

李孝忠，任吉栋

(天津科技大学计算机科学与信息工程学院，天津 300222)

改进的DNA遗传算法在指派问题中的应用

李孝忠，任吉栋

(天津科技大学计算机科学与信息工程学院，天津 300222)

提出了一种基于优秀基因片段思想的DNA遗传算法，将这段基因片段提取出来并将它遗传到后代中，可以加快收敛速度．给出了DNA遗传算法的结构，讨论了选择、交叉和变异算子的具体操作，并将其运用到指派问题最优解的求解中，给出了具体的实现方法．仿真实验验证了算法的有效性和实用性．

DNA计算；遗传算法；指派问题

Abstract：A DNA genetic algorithm based on the thought of excellent gene was proposed，extracting the excellent gene and inheriting it to future generations can speed up the convergence. The structure of DNA genetic algorithm was given and its specific operations including select，crossover and mutation operator were discussed. The method mentioned above was applied to the optimal solution of assignment problem and the concrete implementation was given. The effectiveness and practicality of the algorithm were verified by computer simulation at last.

Keywords：DNA calculation；genetic algorithm；assignment problem

遗传算法是近年来迅速发展起来的一种全新的随机搜索与优化算法，它具有不依赖于问题模型、易于并行处理、有较强的全局搜索功能、鲁棒性强等特点，适用于处理传统搜索方法难以解决的复杂和非线性问题[1]．但是，遗传算法也存在早期收敛[2]和微调能力差[3]等不足．

DNA计算是一种新的计算模式．1994年Adelman首次用实验显示了DNA计算的可能性[4].其最大优点是充分利用了DNA分子具有海量存储遗传密码以及生化反应的海量并行性．近年来，一大批科学家投身于DNA计算这一新的研究领域，提出了许多组合优化问题的DNA计算模型[5]．

为了进一步模拟生物的遗传机理和基因调控机理，一些学者提出了基于DNA编码的遗传算法[6]，并将其用到组合优化问题的求解当中[7]．DNA遗传算法既可以提高DNA计算的效率，又可以拓宽遗传算法的应用范围．DNA遗传算法还需要在常规的遗传算法上进行改进．本文基于优秀基因片段思想提出了选择、交叉和变异操作的新方法来提高进化效率和加快收敛速度．

1 DNA遗传算法

1.1 DNA遗传算法的基本概念

1.1.1 DNA

DNA是在DNA计算中起中心作用的分子，是重要的基因物质，携带着生物的遗传信息．DNA的基本元素是核苷酸，由于化学结构的不同，核苷酸的碱基划分为腺嘌呤(A)、鸟嘌呤(G)、胞嘧啶(C)和胸嘧啶(T)四类碱基．碱基之间的配对关系是：A与T配对，C与G配对，这种配对原则称为Watson-Crick互补性原则．DNA通过磷酸二酯键可组成DNA单链，利用互补性原则，单链很容易形成双链分子．

DNA分子具有变性和复性的性质．DNA变性就是指DNA分子中维持双螺旋稳定性的氢键和疏水键的断裂，使稳定的双螺旋结构松解为无规则线性结构的现象．DNA复性是指变形的DNA链在适当条件下，二条互补链全部或部分恢复到天然双螺旋结构的现象．热变性DNA一般经缓慢冷却后即可复性，此过程称之为“退火”．热循环就是利用这两性质使来源不同的DNA片段按碱基互补关系形成杂交双链分子的一个过程．

1.1.2 生物酶

限制内切酶能够识别特定的碱基序列，并在相应的位置切断作分离操作．聚合酶能够在DNA序列的一端上添加核苷酸使序列加长，作复制操作．

1.2 DNA遗传算法的结构

DNA遗传算法的结构与传统的遗传算法相类似，如图1所示．

1.2.1 DNA编码

使用n个具有任意长度的DNA链组成初始编码群体P(t)．一条DNA链由4种碱基A，T，G，C的序列构成．初始化时，待解问题的设计参数是通过4个字母的符号集 Σ(A，T，G，C)编码以形成染色体，即DNA链．DNA编码是一个关键的环节.DNA链的长短将直接影响问题求解的精度和收敛度．

1.2.2 计算适应度

按照编码规则，根据具体问题构造具体的适应度函数．通过这种评价函数决定哪个染色体是适合问题的最佳解，适应度函数值越大，解的质量越好．

1.2.3 选择

与常规遗传算法类似，从初始编码群体P(t)中以一定的概率选出个体来繁殖后代．经常使用的方法有期望法、精华保存法和适应度比例法等．

1.2.4 交叉

交叉操作是将两条DNA链进行互换重组，其效率和精度直接影响到计算结果．

1.2.5 变异

以一定的概率从DNA群体P(t＋1)中随机地选择若干个个体．随机地选取某一基因位进行变异．变异是为了使DNA遗传算法具有局部随机搜索能力，从而来维持群体的多样性，避免出现早熟现象．

1.2.6 倒位

在DNA链中两个随机选择位置之间的某些碱基的顺序进行倒位．它可以使在父代中离得很远的位在后代中靠在一起．相当于重新定义基因块．倒位操作是可选的，根据问题的需要而定．

2 改进的DNA遗传算法

2.1 改进思想

一个适应度高的个体中包含着一段好的基因片段．将这段基因片段提取出来并将它遗传到后代中，可以加快收敛速度．

2.2 改进技术

基于上述思想，本文在传统DNA遗传算法的基础上对DNA遗传算法做了以下几方面的改进：

选择操作改进．采用“轮盘赌法”选择适应度高的个体，其优点是对适应度低的个体也给予选择的机会，这样保证了优秀基因片段来源的多样性．然后在适应度高的个体中根据一定的规则选择出一段优秀的基因片段．确定一个长度L，从选出的每个适应度高的个体中随机选出n个长度为L的子序列，从中选出适应度最高的作为优秀基因片段．

交叉操作改进．丁永生等[8]提出了采用基因转移操作来取代交叉算子．将染色体中某一段好的基因串直接传递给其他染色体，进行信息之间的重组．从而产生更好的个体，来加快搜索速度．本文以此为基础，分两种情况产生新的群体．适应度高的个体按照一定的概率进行优秀基因片段的互换，适应度低的个体分别以优秀基因片段为母体随机产生新的个体．

变异操作改进．为保持种群的多样性和产生新的基因信息，变异操作在所有新个体中进行．文献[9]在研究DNA序列模型时指出在同一个DNA序列的不同位置，存在hot spot和cold spot，位于cold spot的碱基其变异概率远远小于hot spot的碱基．对于DNA遗传算法而言，在进化的不同阶段，不同位置的码位对问题答案的影响是不一样的．基于上述思想，变异概率应该是一个动态变化的过程，变异的方法也与传统的单个基因位的变异不同．从所有DNA链中选出适应度最高的个体，随机地选取该DNA链中的某一段DNA序列，将其传递给其他个体的对应部分．

2.3 算法编码及操作算子

2.3.1 编码

DNA序列采用A、G、C、T四个字母来对长度为L，由腺嘌呤、鸟嘌呤、胞嘧啶、胸腺嘧啶四种碱基组成的DNA序列进行编码．

2.3.2 操作算子

(1),选择算子．根据适应度函数值f，采用“轮盘赌法”定义最好的N/2个个体为中性个体，剩下的为有害个体．为便于计算，设N为偶数．在N/2个中性个体中选出N/2个长度为l0的优秀基因片段，即当前序列的子序列R．

(2),交叉算子．交叉分两种情况：中性个体两两互换优秀基因片段，两个序列与对方子序列R相对应的地方分别被对方的子序列R所替换；有害个体交叉的概率为100%．通过两种情况的交叉操作得到N个子代个体．

(3),变异算子．根据问题的特点选择是否使用动态的变异概率．

3 改进的DNA遗传算法求解指派问题

3.1 指派问题

指派问题的提法是：某单位需完成n项任务，恰好有n个人可承担这些任务．各人完成任务不同，效率也不同.那么，如何进行指派，使总效率最高呢?

设决策变量为xij(i，j＝1，2，…，n)，当指派第i个人去完成第j项任务时，xij＝1；否则，xij＝0．设第i个人完成第j项任务的时间为cij(i，j＝1，2，…，n)，cij＞0．若要求指派后的总时间最小，则最优指派问题的数学模型为

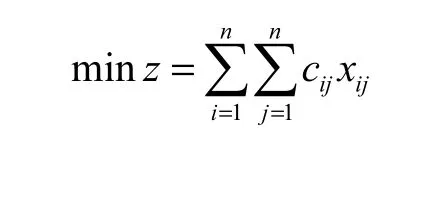
从模型中的约束条件的结构不难看出：设决策变量所组成的矩阵为A＝(xij)n×n，则最优指派问题的解xij(i，j＝1，2，…，n)为可行解的充分必要条件为A中恰有n个数为1，第j列恰有1个数为1(j＝1，2，…，n)，第i(i＝1，2，…，n)行恰有1个数为1．

3.2 算法编码及算法步骤

3.2.1 DNA编码

根据指派问题的特点，对每个人的每项任务进行编码，n项任务n个人来完成总共需要n×n个编码．编码包括3 bp(base pairs)长度的数值序列和10 bp长度的标志序列，分三种情况．第一列的编码先是数值序列，然后是标志序列；最后一列的编码与第一列的正好相反，先标志序列再数值序列；中间列为两个标志序列中间夹一个数值序列．如果有后标志序列，则它唯一地表示了该列，如果有前标志序列，则它是前一列后标志序列的补序列．例如第一列的编码为XXXAACGTGATGC，第二列的编码为TTGCACACGXXXGTAGCTAGTG．其中XXX为数值序列，表示此人完成该任务所需的时间．第一列编码中的后标志序列AACGTGATGC表明该编码为第一列编码．至于编码属于哪一行则通过添加药剂来实现．从编码得出每个序列的长度为13×n－10．

3.2.2 算法步骤

(1)设置最大进化代数G和初始种群数N．将n×n个编码片段放在一起进行热循环，在热循环过程中前一列的后标志序列和与它互补的后一列的前标志序列退火，在聚合酶的作用下形成双链．在聚合前，为每一行的n个片段设置相同的特性标记，为每一列设置不同的特性标记，使得处在相同行不同列的片段互相排斥不能连接，并且这些标记可以叠加，保证已经连接的片段不能再与该片段上已有的处在相同行上的片段相连．在此基础上得到N个DNA序列作为初始种群．

(2)初始种群中每个序列的单链部分就是每个人完成任务所需的时间．根据适应度将N个DNA序列分成两部分．本文的适应度函数设计如下：

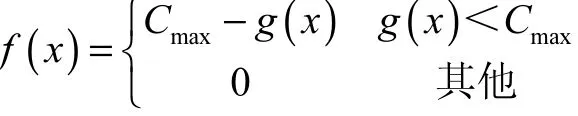
式中：g(x)是相应指派方案中所有人的完成时间和；Cmax为进化过程中g(x)的最大值或当前群体中g(x)的最大值．从公式可以看出，完成时间和小的指派方案相应的适应度值大，所以保留的可能性也较大．采用“轮盘赌法”将适应度高的N/2个个体保存下来，并从这些个体中提取出N/2个优秀片段．从1到[n/2]中随机生成一个数a，在N/2个体中截取N/2个从a列到a＋[n/2]–1列长度为[n/2]的片段，为了满足这个要求，用限制性酶的特殊酶切位点来完成．然后计算每个的时间值，选择时间最短的．重复执行N/2次，产生N/2个优秀片段．

(3)分别以步骤(2)产生的优秀片段为母板，继续与n×n个片段进行热循环，产生N/2个带有优秀片段的新个体，与保存下来的时间短的N/2个个体组成新的N个个体．

(4)由于问题的编码不涉及到高低位，所以不采用动态变异概率．设定一个变异概率p，对每个个体都产生一个随机概率pi，如果pi≤p则进行变异．变异时从1到n中随机生成一个数b，将序列中的第b个片段剪切下来，这样产生两段序列，并将第二段序列的最后一个片段也去掉．然后将剩下的两段序列放在不包含剪切下来的两个片段的试管中进行热循环，将两段序列连接产生新的DNA序列．

将上述步骤产生的种群重复进行步骤(2)、(3)、(4)的操作G－1次，得到最优解．

4 仿真实验

根据上述步骤将DNA编码改成实数编码，所有的生物操作采用编程实现，在Visual C++环境下采用C++语言编写程序进行仿真．设有A、B、C、D、E、F、G、H八项任务由0、1、2、3、4、5、6、7八个人去完成，其完成时间如表1所示．实验参数为：最大进化代数G为20、初始种群N为10、变异概率p为0.1．

表1 8×8指派问题时间数据Tab.1 Tim e data of 8×8 assignm ent problem d

实验表明，平均迭代4.5次就可以收敛到最优方案：7A—3B—6C—0D—1E—5F—4G—2H，而传统的DNA遗传算法平均迭代9.5次才能达到最优解．改进前后的实验对比见表2．可以看出，改进后的方法收敛更快．

表2 改进前后的实验对比Tab.2 Results of com parison experiment

5 结 语

本文在传统DNA遗传算法的基础上，根据优秀基因片段思想，对选择、交叉和变异操作进行改进，给出了具体操作．针对指派问题的最优解求解，提出具体的算法步骤，并进行仿真，初步验证了改进算法的有效性和实用性．但是对于如何选择优秀基因片段本文并没有给出确定的规则，需要根据具体的问题进行具体的分析，还需要在这方面进行进一步的研究．

［1］ 俞国燕，王筱珍. 改进遗传算法的应用研究[J]. 机械制造，2007，45(513)：58–60.

［2］ 蒋腾旭，谢枫. 遗传算法中防止早熟收敛的几种措施[J]. 计算机与现代化，2006，136(12)：54–56.

［3］ 徐丽娜. 神经网络控制[M]. 哈尔滨：哈尔滨工业大学出版社，1999：1–15.

［4］ Adelman L M. Molecular computation of solutions to combinatorial problems [J]. Science，1994，266(5187)：1021–1024.

［5］ 丁永生. 计算智能：理论、技术与应用[M]. 北京：科学出版社，2004：294–303.

［6］ 丁永生，任立红. DNA遗传算法及其函数寻优应用[C]//中国控制与决策学术年会论文集. 沈阳：控制与决策编辑部，2000：235–239.

［7］ 张雷，杨大地，冉戎. 基于DNA遗传算法的曲面最短路径问题[J]. 计算机工程，2007(16)：181–185.

［8］ Ren L H，Ding Y S，Ying H，et a1. Emergence of selflearning fuzzy systems by a new virus DNA-based evolutionary algorithm [J]. Intelligent Systems，2003，18(3)：339–354.

［9］ Neuhauser C，Krone S M. The genealogy of samples in models w ith selection[J]. Genetics，1997(2)：519–534.

Im proved DNA Genetic A lgorithm and Its App lication to Assignment Problem

LI Xiao-zhong，REN Ji-dong
(College of Computer Science and Information Engineering，Tianjin University of Science & Technology，Tianjin 300222，China)

TP18

A

1672-6510(2011)02-0061-04

2010–11–04；

2011–01–11

国家自然科学基金资助项目(61070021)

李孝忠（1962—），男，山东人，教授，博士，lixz@tust.edu.cn．