螺纹旋合长度对钢轨接头螺栓强度的影响分析

李 响，薛 强，苗德华

(天津科技大学机械工程学院，天津 300222)

螺纹旋合长度对钢轨接头螺栓强度的影响分析

李 响，薛 强，苗德华

(天津科技大学机械工程学院，天津 300222)

应用有限元接触分析方法，研究钢轨接头螺栓螺纹旋合长度对螺栓强度的影响．通过改变钢轨接头螺栓和螺母的螺纹旋合长度，并进行相应的接触有限元分析，定量研究钢轨接头螺栓内部的应力分布，为实现钢轨螺栓螺母的轻量化，降低螺栓和螺母的制造成本提供理论依据．

钢轨螺栓；螺纹旋合长度；有限元分析；疲劳强度

Abstract：By using finite element contact analysis method，the influence of the length of thread engagement on the strength of rail bolt was analyzed. Through changing the length of thread engagement of rail bolt and carrying on the finite element contact simulations，the quantitative research of stress distribution w ithin the rail bolt was completed. And through which，a theoretical foundation for the realization of lightweight of rail bolts and nuts，and the reduction of manufacture costs was provided.

Keywords：rail bolt；length of thread engagement；finite element analysis；fatigue strength

铁路运输不断向高速、重载发展，列车的轴重、行车密度和速度不断增加，钢轨的负荷量也不断增加．钢轨接头螺栓是铁路钢轨联接的重要零件，其强度决定着铁路钢轨联接的安全性和可靠性．我国铁路发展很快，里程不断增加，高速铁路里程已居世界第一位，高强度接头螺栓和螺母用量巨大．研究螺纹旋合长度对钢轨接头螺栓强度的影响，在保证联接强度的前提下适当减少螺纹旋合长度，实现钢轨螺栓螺母的轻量化非常重要．国内对钢轨螺栓联接强度的研究，主要集中在改变螺栓螺纹根部的圆角半径[1]、螺栓螺母的结构[1–2]等，有关螺栓螺纹旋合长度对螺栓强度的影响，目前还未见有非常详细的定量分析和研究．

本文应用有限元接触分析方法，研究钢轨接头螺栓螺纹旋合长度对螺栓强度的影响．通过改变钢轨接头螺栓和螺母的螺纹旋合长度，并进行相应的接触有限元分析，定量研究钢轨接头螺栓内部的应力分布，为实现钢轨螺栓螺母的轻量化，降低螺栓和螺母的制造成本提供理论依据．

1 钢轨螺栓联接结构及螺栓主要参数

钢轨螺栓联接由钢轨、螺栓、螺母、缓冲垫等组成，如图1所示．

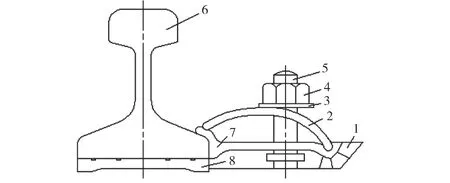
图1 钢轨螺栓联接示意图Fig.1 Joint schematic diagram of the rail bolt

采用适用于无缝线路、钢轨间距55,cm、60,kg/m钢轨接头联接用的螺栓和螺母作为计算模型．螺栓为10.9级高强度绝缘接头螺栓，材料采用20,MnTiB，其抗拉强度为1 040,MPa，屈服强度为940,MPa；材料的泊松比为0.28，弹性模量为210,GPa；采用普通三角螺纹，基本牙形参见文献[3]．钢轨螺栓的基本结构如图2所示，螺栓长度为150,mm，螺纹长度为60,mm，公称直径为24,mm，螺距为3,mm，螺纹中径为22.051,mm．螺栓联接的其他结构参数参见文献[4]．

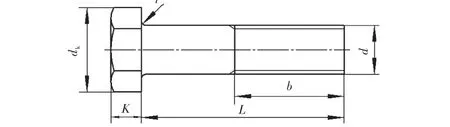
图2 钢轨螺栓主要参数Fig.2 M ain parameters of rail bolt

2 螺栓联接有限元模型建立

2.1 几何模型

选取旋合长度为3～10个螺距的8种螺栓联接形式，建立其几何模型．图3所示为其中的部分几何模型(局部)．

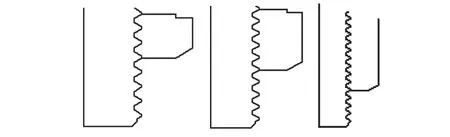
图3 不同旋合长度的联接几何模型Fig.3 Geometric m odels of different length of thread Fig.3草 engagement

2.2 单元网格划分

采用两自由度四边形轴对称平面单元进行网格划分，网格划分原则参考文献[1]．为了控制单元划分质量，四边形角度限制为70°～110°，单元边长的最大长度为0.02,mm，不同旋合长度螺栓联接的单元数和节点数见表1．图4为其中一种螺栓联接形式的有限元网格模型(局部)．

2.3 接触模型建立

由于螺栓和螺母相互接触，不能把它们看作同一个物体进行有限元分析计算，应该按接触分析处理．由于接触问题是一种高度非线性行为，需要很大的计算资源，为了实现高效率、高精度和稳定性的计算，必须建立合理的有限元接触模型．本文采用两维面–面接触单元建立接触对，接触求解算法采用增广拉格朗日(Augmented Lagrangian)方法，材料的摩擦因数为0.15．

表1 不同旋合长度的网格划分数据Tab.1 M esh data of different length of thread engagement

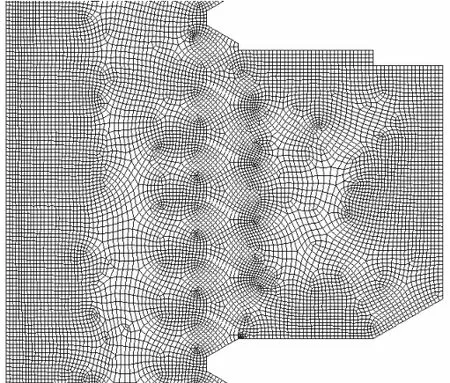
图4 网格划分实例Fig.4 M eshing model exam p le

2.4 载荷及边界条件

螺栓联接的加载方式及边界约束条件[1–2]参见图5．根据螺栓联接的特点，按照轴对称方法进行加载和约束，即在OX处加轴向约束，使其Y方向位移为0；在OY上施加径向约束，使其X方向位移为0；在螺母与被联结物体接触面上施加5 MPa的轴向载荷．

图5 加载方式Fig.5 Loading way

3 计算结果及分析

3.1 计算结果

在螺栓联接有限元模型建立后，采用ANSYS对8种旋合长度的联接进行有限元接触分析计算．

不同旋合长度螺栓联接形式的最大工作应力(Von M ises stress)及其位置见表2．表中最大工作应力位置为YO方向距螺栓端部的距离．不同旋合长度螺栓联接形式的应力云图如图6所示．图中螺栓联接的方位为OY方向，即螺母的上面位置为支承面，螺栓联接承受的载荷施加在该支承面上．

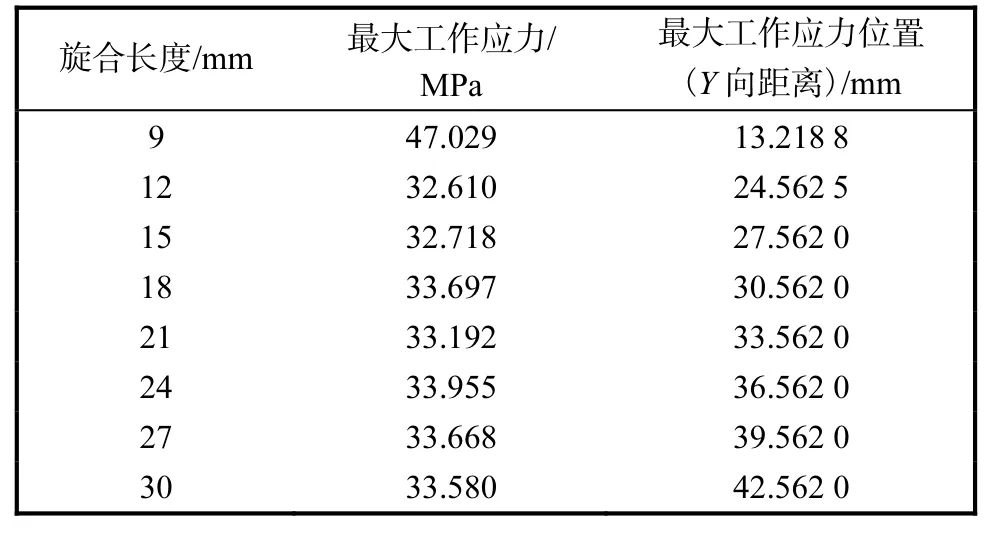
表2 最大工作应力及其位置Tab.2 M aximum Von M ises stress and their positions

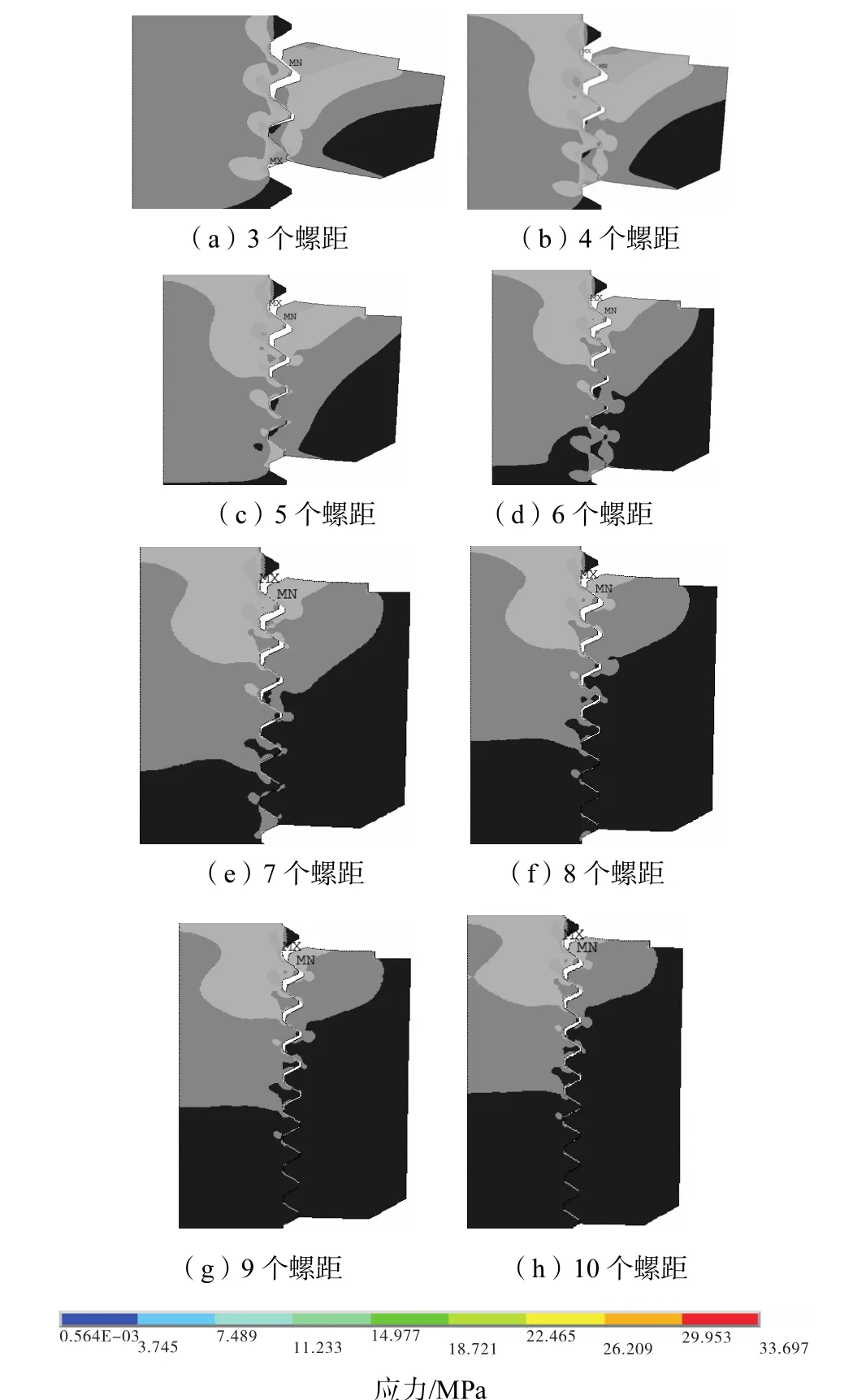
图6 不同旋合长度螺栓的应力云图Fig.6 Stress contours of different length of thread engagement

3.2 不同旋合长度螺栓的应力分布

从表2所示的螺栓最大工作应力及其位置，以及图6所示的螺栓联接应力云图可知：旋合长度为3个螺距时，最大工作应力出现在从螺栓联接支承面开始的第3圈，且数值较大；其他旋合长度的螺栓最大工作应力均出现在第1圈．根据已有的文献和实验可知[5–7]，螺栓联接的失效一般是由螺栓的疲劳断裂造成的，而且断裂通常发生在从螺栓联接支承面开始的第1圈．因此，从计算结果分析，旋合长度在4个螺距及以上时，结果是比较合理的．而对于3个螺距的旋合长度，其应力的不同状态和数值应该是因为较短的螺纹旋合长度所致．

旋合长度为4～10个螺距时，其第2圈的最大工作应力分别为26.077、23.815、22.621、22.727、22.012、22.364、22.080,MPa．可以看出，从旋合长度为6个螺距开始，其第2圈的最大工作应力基本相同，而且第2圈的最大应力值与相应的螺栓联接最大工作应力值(第1圈处)的差也基本相同．通过分析可知，螺栓联接其他位置的应力也有这种趋势．说明螺栓联接的应力分布有一定规律．因而，从螺栓联接应力分布来看，旋合长度为6～10个螺距的变化不大，其联接的疲劳强度基本相同．

从图6所示的螺栓联接应力云图可知，螺栓所受到的拉应力主要集中在从螺栓联接支承面开始的第1至第7圈，而从第8至第10圈，螺栓所受到的拉应力较小，其对螺栓疲劳强度的影响也较小．

4 结 论

(1)钢轨螺栓联接的最大工作应力出现在从螺栓联接支承面开始的第1圈接触面处，考虑到已有的文献、实验结果[5]和本文所做有限元分析，螺纹旋合长度最少应该是4个螺距．

(2)计算结果表明，螺栓所受到的拉应力主要集中在从螺栓联接支承面开始的第1至第7圈，而从第8到第10圈，螺栓所受到的拉应力较小，其对螺栓疲劳强度的影响也较小．因此，减小螺栓和螺母的旋合长度，以节省材料降低成本，而螺栓的疲劳强度并不会明显改变．

(3)目前铁路上实际使用的联接螺栓和螺母的旋合长度为27,mm(9个螺距)，标准上规定的旋合长度是24,mm．从本文有限元接触分析的结果看，钢轨螺栓螺纹旋合长度推荐采用6个或7个螺距，这样可以使材料得到充分利用，螺纹旋合长度可以减少，螺栓的长度也可以降低，从而实现钢轨螺栓联接的轻量化．

(4)在螺栓长度减小后，可能会造成螺栓刚度的增加，从而造成螺栓应力幅度的增大，疲劳强度减小．可以通过改变螺栓的结构，如减小螺栓的直径，或采用中空螺栓，增加螺栓的柔性来解决这个问题．这样还可以进一步实现钢轨螺栓联接的轻量化．

(5)文献[5]进行了钢轨螺栓的疲劳实验，其实验结果与本文有限元分析的结果基本吻合．考虑到钢轨螺栓在使用时受到的冲击和振动，在后续的研究中可以进一步考虑这种情况，以提高有限元分析的精度．

［1］ 薛强，苗德华，汪文颖. 钢轨螺栓螺纹根部圆弧半径对螺栓强度的影响[J]. 天津科技大学学报，2004，19(1)：52–54.

［2］ 薛强，苗德华. 钢轨接头螺栓的有限元应力集中分析[J]．铁道标准设计，2004(4)：70–72.

［3］ 全国螺纹标准化技术委员会. GB/T 192—2003普通螺纹·基本牙型[S]. 北京：中国标准出版社，2003.

［4］ 铁道部标准计量研究所. TB/T 2347—1993 钢轨用高强度接头螺栓与螺母[S]. 北京：中华人民共和国铁道部，1993.

［5］ 白卫卫. 钢轨螺栓结构优化设计及其疲劳特性的研究[D]. 天津：天津科技大学机械工程学院，2005.

［6］ 濮良贵，纪名刚. 机械设计[M]. 北京：高等教育出版社，2001.

［7］ 马履中. 机械原理与设计[M]. 北京：机械工业出版社，2009.

Influence of the Length of Thread Engagement on the Strength of Rail Bolt

LI Xiang，XUE Qiang，M IAO De-hua
(College of Mechanical Engineering，Tianjin University of Science & Technology，Tianjin 300222，China)

TH13.3

A

1672-6510(2011)02-0045-04

2010–11–12；

2010–12–23

李 响（1983—），男，天津人，硕士研究生；通信作者：薛 强，教授，qxue@tust.edu.cn．