内禀正则半群的新刻画

林秀萍，谢祥云

（五邑大学 数学与计算科学学院，广东 江门 529020）

内禀正则半群的新刻画

林秀萍，谢祥云

（五邑大学 数学与计算科学学院，广东 江门 529020）

介绍了内禀正则半群上的区间值模糊集，探讨了它们之间的一些运算性质，并用区间值模糊左（右，双）理想给出了内禀正则半群的新刻画.

内禀正则半群；区间值模糊集；区间值模糊左（右，双）理想

1965年Zadeh首先提出了模糊集的概念，1975年Zadeh[1]提出了模糊集的另一个重要概念：区间值模糊集. 进一步地，很多数学家讨论了直觉模糊子集[2-6]以及它们上的算子[3,7-8]. 1994年，Biswas[9]在Rosenfeld模糊子群的基础上类似地定义了区间值模糊子群，讨论了它们的有关性质. 在半群和序半群研究的基础上[10-12]，近来，Narayanan等[13]引入了半群的区间值模糊左（右，双，内禀）理想并讨论了一个区间值模糊左（右，双，内禀）理想的生成问题，2008年Shabir等[14]将该结论进一步推广到序半群的情况. 本文讨论了内禀正则半群上的区间值模糊左（右，双）理想并通过它们给出了内禀正则半群的新刻画.

本文设S是半群. S称为正则的，如果(∀x∈S)(∃y∈S)x=xyx. 设A≠∅，A⊆S，A称为S的左理想，如果SA⊆A；A称为S的右理想，如果AS⊆A. 一个非空子集A既是S的左理想又是S的右理想，则称之为S的理想. S的子半群B如果满足BSB⊆B，则称B为S的双理想. 半群S称为内禀正则的，如果(∀a∈S)(∃x,y∈S)a=xa2y ，即(∀a∈S)a∈Sa2S . 半群S的模糊子集f称为模糊子半群，如果(∀x,y∈S)f(xy)≥min{f(x),f(y)}. f称为S的模糊左（右）理想，如果(∀x,y∈S)f(xy)≥f(y)(或f(xy)≥f(x)). 如果f既是模糊左理想又是模糊右理想，称f为S的模糊理想[13]，即(∀x,y∈S)f(xy)≥max{f(x),f(y)}.

本文涉及的其他术语或概念参见文献[12,15].

1 区间值模糊子半群

用D[0,1]表示[0,1]的所有闭子区间集，为了方便，将[c,c]，∀c∈[0,1]也归入D[0,1]. 设=[a-,a+]，，∀i∈I均为D[0,1]中的元素，D[0,1]集上规定的大小及相等关系如下：

设S是半群，S的区间值模糊子集（interval valued模糊子集，简称i-v模糊子集）是一个从S到D[0,1]的映射. 设f为S的i-v模糊子集，则对任意x∈S,f(x)=[f-(x),f+(x)],f-(x)≤f+(x)，这里f-和f+分别是f诱导的2个S的模糊子集. 设A⊆S,A≠∅，则

是S的i-v模糊子集.

设S为半群，f,g是S的2个i-v模糊子集，规定它们之间的大小关系及运算如下：

1）(∀x∈S)f≤g当且仅当f(x)≤g(x).

2）(f∪g)(x)=rmax{f(x),g(x )}.

3）(f∩g)(x)=rmin{f(x),g(x )}.

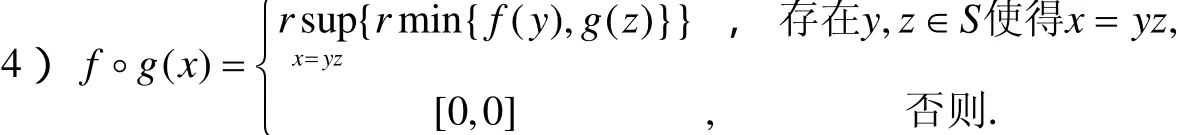
定义1[13]456设S为半群. S的i-v模糊子集f称为S的i-v模糊半群，如果

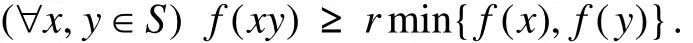
定义2[13]456设S为半群. S的i-v模糊子集f称为S的i-v模糊左理想（右理想），如果

如果f既是i-v模糊左理想又是i-v模糊右理想，则称之为S的i-v模糊理想.

定理1 S的i-v模糊子集f是i-v模糊理想当且仅当

证明 必要性. 因为f是i-v模糊理想，所以

因此f(xy)≥rmax{f(x),f(y)}.

充分性. 如果f(xy)≥rmax{f(x),f(y)}，显然，f(xy)≥f(x)且f(xy)≥f(y).

定义3[11]5设S是半群. S的i-v模糊子集f称为S的i-v模糊双理想，如果

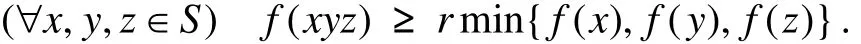
因此，S的每个i-v模糊左（右）理想一定是S的i-v模糊双理想.

定义4[15]设S是半群. S的i-v模糊子集f称为S的i-v模糊内禀理想，如果

注意到S本身的特征函数，即fS(x)=[1,1]，∀x∈S是S的i-v模糊理想，我们仍然记之为S.

2 主要定理

首先给出以下引理.

引理1[15]106设S为半群，下列各款等价：

1）S是内禀正则的.

2）对S的每个左理想L和每个右理想R，R∩L⊆LR ．

引理2[13]设S为半群，下列各款等价：

1）S是正则和内禀正则的.

2）对S的每个双理想B，B2=B.

3）对S的任何2个双理想A、B，A∩B⊆A◦B .

4）对S的每个双理想B和每个左理想L，B∩L⊆LB∩BL .

5）对S的每个双理想B和每个右理想R，R∩B⊆BR∩RB.

6）对S的每个左理想L和每个右理想R，R∩L⊆LR∩RL .

定理2 设半群S的非空子集A是S的左（右，双）理想当且仅当fA是S的i-v模糊左（右，双）理想．

证明 设S为半群，A为S的左理想，则SA⊆A．设∀x,y∈S，若xy∈SA，则xy∈A，即fA(xy)=[1,1]≥fA(y). 若xy∉SA，则xy∉A，且y∉A，所以fA(xy)=[0,0]≥[0,0]=fA(y). 综上所述，∀x,y∈S均有fA(xy)≥fA(y). 所以fA是S的i-v模糊左理想．反之，显然. 同理可以证明i-v模糊右理想和双理想这两种情况.

定理3 设S是半群，f是S的i-v模糊左理想当且仅当S◦f≤f.

证明 设S为半群，f是S的i-v模糊左理想，∀x,y∈S，如果存在∀y,z∈S使得x=yz，则

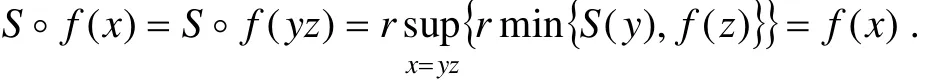
否则S◦f(x)=0≤f(x). 因此，S◦f≤f. 反之，如果S◦f≤f，则对∀y,z∈S，

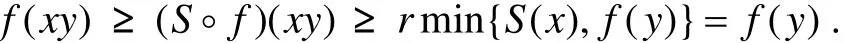
同理可以证明下面的对偶情形.

定理4 设S是半群，f是S的i-v模糊右理想当且仅当f◦S≤f.

定理5 设S为半群，S是内禀正则的当且仅当对每个i-v模糊理想f均有f(a)=f(a2),∀a∈S .

证明 设f是S的i-v模糊理想，a∈S. 设S是内禀正则的，则存在x,y∈S使得a=xa2y，因此

故f(a)=f(a).

反之，设a∈S，则a2生成的理想是(a2)，由定理2，f(a2)为S的i-v模糊理想，根据假设，f(a2)(a)=f(a2)(a2)=[1,1]，因此a∈(a2)={a2}∪Sa2∪a2S∪Sa2S . 由此推出a∈Sa2S，所以S是内禀正则的．证毕．

推论1 设S是内禀正则半群，则对于每个i-v模糊理想f，f(xy)=f(yx)，∀x,y∈S.

证明 由定理5，

因此，f(xy)=f(yx).

定理6 设半群S，则S是内禀正则的当且仅当对S的每个i-v模糊左理想f和每个i-v模糊右理想g，f∩g≤f◦g．

证明 设S是内禀正则半群且f,g分别是S的i-v模糊左、右理想. 对任意a∈S，存在x,y∈S使得a=xa2y，且

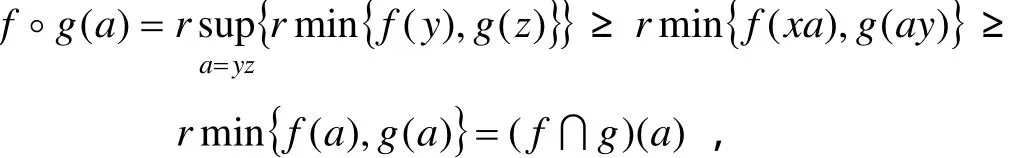
因此，f∩g≤f◦g.

反之，如果f∩g≤f◦g，设R,L分别是S的右理想和左理想. 由定理2，则fR,fL是S的i-v模糊右理想和左理想. 设a∈R∩L，则，

因此存在x∈R,y∈L使得a=xy，即a∈RL. 由引理1，S是内禀正则的.

引理3[15]103一个半群是正则的当且仅当对S的每个右理想A和每个左理想B，A∩B=AB.

引理4 一个半群是正则的当且仅当对S的每个i-v模糊左理想f和每个i-v模糊右理想g，f∩g=f◦g.

证明 设S是正则的，因为f为i-v模糊左理想，所以f◦g≤f◦S≤f. 因为g为S的每个i-v模糊右理想，所以f◦g≤S◦g≤g，因此f◦g≤f∩g. 另一方面，对任意a∈S，因为S为正则半群，所以存在x∈S使得a=axa. 因此，

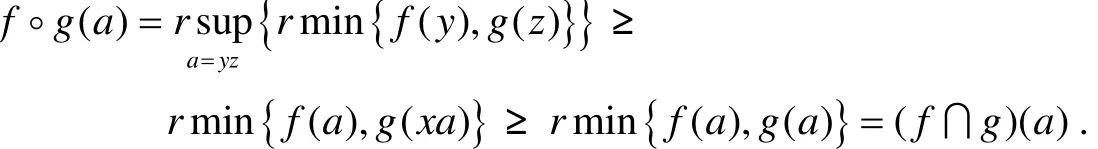
综上证明，有f∩g=f◦g.

反之，设A为S的左理想，B为S的右理想，则fA,fB分别是S的i-v模糊左理想和右理想，由假设，fA∩fB=fA◦fB. 取a∈A∩B，则[1,1]=(fA∩fB)(a)=fA◦fB(a). 因此，故a∈AB. 显然AB⊆A∩B.

因此，AB=A∩B. 由引理3，S是正则的.

定理7 设S是半群，下列各款等价：

1）S是正则和内禀正则的.

2）对S的每个i-v模糊双理想f，f◦f=f.

3）对S的任意i-v模糊双理想f,f1，f∩f1≤(f◦f1)∩(f1◦f).

4）对S的每个i-v模糊双理想f和每个i-v模糊左理想h，f∩h≤(f◦h)∩(h◦f).

5）对S的每个i-v模糊双理想f和每个i-v模糊右理想g，f∩g≤(f◦g)∩(g◦f).

6）对S的每个i-v模糊右理想g和每个i-v模糊左理想h，g∩h≤(g◦h)∩(h◦g).

证明 显然3）⇒4），4）⇒6），3）⇒5），5）⇒6），3）⇒2）.

1）⇒3）. 任意a∈S. 因为S是正则的，则存在x∈S使得a=axa=axaxa，又因为S是内禀正则的，则存在y,z∈S使得a=ya2z. 所以

因为f,f1是S的i-v模糊双理想，所以

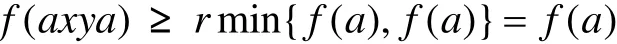
且

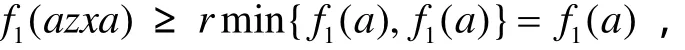
所以

所以，f◦f1≥f∩f1．同理可证f1◦f≥f∩f1，因此

6）⇒1）. 设6）成立. 设g,h分别是S的任意2个i-v模糊右理想和左理想，由题意知：

由定理6可得S是内禀正则的. 另一方面，根据定理4和定理5，g∩h≤g◦h≤g◦S≤g，g∩h≤g◦h≤S◦h≤h，得g∩h≤g◦h≤g∩h，即g◦h≤g∩h. 由引理4，S是正则的.

2）⇒1）设B是S的任意双理想，则fB是S的i-v模糊双理想，显然B2⊆B. 取∀a∈B，因为fB◦fB=fB，所以

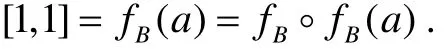
因此Ω={(b,c)∈B×Ba=bc}≠∅，故a∈B2，即B=B2. 由引理2，S是正则和内禀的.

[1] ZADEH L A. The concept of a linguistic variable and its application to approximate reason[J]. Inform Control, 1975, 18: 199-249.

[2] ATANASSOV K, GARGOV G. Interval valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1989, 31: 343-349.

[3] ATANASSOV K. Operations over interval valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1994, 64: 159-174.

[4] BUSTINCE H, BURILLO P. Correlation of interval-valued intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1995, 74: 237-244.

[5] BURILLO P, BUSTINCE H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets[J]. Fuzzy Sets and Systems, 1996, 78: 305-316.

[6] DESCHRIJVER Glad, KERRE Etienne E. On the relationship between some extensions of fuzzy set theory[J]. Fuzzy Sets and Systems, 2003, 133: 227-235.

[7] DESCHRIJVER Glad. Arithmetic operation in interval-valued fuzzy set theory[J]. Inform Sci, 2007, 177: 2906-2924.

[8] PARK Jinhan, LIM Kimoon, PARK Jongseo, et al. Distances between interval-valued intuitionistic fuzzy sets[J]. Journal of Physics (Conference Series), 2008, 96: 12-89.

[9] BISWAS R. Rosenfeld’s fuzzy subgroups with interval-valued membership functions[J]. Fuzzy Sets and 1 Systems, 1994, 63: 87-90.

[10] HONG Yongfa, FANG Xianwen. Characterizing intraregular semigroups by intuitionistic fuzzy sets[J]. Mathware Soft Computing, 2005, 12: 121-128.

[11] XIE Xiangyun, TANG Jian. Regular ordered semigroups and intraregular ordered semigroups in terms of fuzzy subsets[J]. IJFS, 2010, 7(2): 121-140.

[12] 谢祥云. 序半群引论[M]. 北京：科学出版社，2001.

[13] NARAYANAN AL, MANIKANTAN T. Interval-valued fuzzy ideals generated by an interval-valued fuzzy subset in semigroups[J]. J Appl Math Computing, 2006, 20(1/2): 455-464.

[14] SHABIR M, ISRAR All Khan. Interval-valued fuzzy ideals generated by an interval-valued fuzzy subset in ordered semigroups[J]. Mathware Soft Computing, 2008, 15: 263-272.

[15] 谢祥云，吴明芬. 半群的模糊理论[M]. 北京：科学出版社，2005.

A New Characterization of Intra-regular Semi-groups

LIN Xiu-ping, XIE Xiang-yun
(School of Mathematics and Computation Science, Wuyi University, Jiangmen 529020, China)

The concept of intraval valued fuzzy sets on intra-regular semi-groups is introduced. Moreover, the operations with interval valued fuzzy sets are discussed. Finally, some theorems are given to characterize intra-regular semigroups in terms of interval valued fuzzy left (resp. right, bi-) ideals of semigroups.

intra-regular semi-groups; interval valued fuzzy sets; interval valued fuzzy left (right, bi) ideal

O152. 7

A

1006-7302（2011）01-0010-06

2010-08-20

国家自然科学基金资助项目（10961014）；广东省自然科学基金资助项目（0501332）

林秀萍（1984—），女，广东阳江人，硕士研究生，研究方向：模糊代数；谢祥云，教授，博士，硕士生导师，通信作者，研究方向为序半群的代数理论、模糊代数、粗糙集理论.