光滑函数芽的无限相对决定性

贺文青，徐沈新

（保险职业学院 金融保险系，湖南 长沙 410114）

光滑函数芽的无限相对决定性

贺文青，徐沈新

（保险职业学院 金融保险系，湖南 长沙 410114）

在(Rn,0)中一般代数集芽S上，讨论了光滑函数芽在右等价群ℜ的子群ℜS作用下其无限相对决定性的条件，所得结果推广了Wilson的有关定理.

函数芽；代数集；无限决定性

无限决定性研究了光滑函数芽在平坦芽扰动下的稳定性. 国内外有大量关于光滑映射芽无限决定性的研究，Brodersen等[1]研究了映射芽的无限决定性和拓扑C0决定性，C.T.C.Wall[2]研究了等变映射芽的无限决定性，L.C. Wilson[3-4]研究了映射芽关于左右等价群和右等价群的无限决定性，Sun B.等[5]研究了实孤立线奇点芽在右等价群子群ℜL作用下的无限决定性，刘恒兴等[6]讨论了分支问题的无限决定性. 本文就函数芽在右等价群ℜ的子群ℜS作用下的无限相对决定性做了一些讨论.

记εn={f:(Rn,0)→R∈C∞}为光滑函数芽环，为ε的极大理想. 对于nf∈εn，记，εn为芽f的雅可比理想，jrf可表示f在0∈Rn处的r阶 Taylor多项式. 记ℜ表示右等价群，f◦ℜ={f◦φ|φ∈ℜ}表示f在群ℜ作用下的轨道，Tf(f◦ℜ)表示f◦ℜ在f处的轨道切空间. 考虑由所有平坦芽构成的理想

定义1 设f∈εn，称f是无限ℜ-决定的（简称为∞-ℜ-决定的），如果对于∀u∈，都存在光滑微分同胚φ∈ℜ使得f+u=f◦φ.

定理1[3]70-72设f∈μn，则下面的条件等价：

1 定义和结果

假设S为(Rn,0)中包含原点的代数集芽，考虑右等价群ℜ的子群ℜS={φ∈ℜ|φ|S=idS}.

定义2 设f∈εn，如果对于∀u∈IS∩，都存在光滑微分同胚φ∈ℜS使得f+u=f◦φ，则称f相对于ℜS是∞-ℜS-决定的，其中IS={f∈εn|f |S≡0}是εn的理想.

显然f是∞-ℜS-决定的当且仅当f+IS∩⊂f ◦ℜS.

定义3 设I是环εn的一个理想．令S=z(I)={x∈Rn|f(x)=0,∀f∈I }并假设0∈S．令radI={f∈εn|f|S≡0}，如果I=radI，则称I是εn的一个根式理想．设S⊂(Rn,0)且存在R[x]的理想I使得S=z(I)，则称S是代数集芽.

定理2 设f∈μn，S⊂(Rn,0)为一代数子集芽，则f是∞-ℜS-决定的当且仅当IS∩⊂Tf(f ◦ℜS).

注：若S={0}，则IS=μn，Tf(f◦ℜS)=μnJ(f )，定理2退化为定理1的结果．

2 定理2的证明

引理1 如果S⊂(Rn,0)是一个代数集芽，则理想IS={f∈εn|f |S≡0}是εn的根式理想．

证明 由代数集的定义，则存在理想I⊂R[x]使得S=z(I)且I⊂IS⊂μn．由理想的根的定义，则radIS={f∈μn|f |z(IS)=0}，故我们只需证S=z(IS)．

以下证明定理2.

证明 充分性. 假设f是∞-ℜS-决定的，则由定义2有

由于f+IS∩是εn的R-向量子空间，对式（1）两边在f取轨道切空间即可.

必要性. 设g∈εn满足g-f∈IS∩，只需证明g与f是ℜS-等价的．

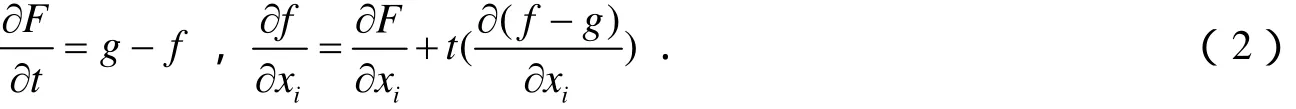
下面证明对于任意的t0∈[0,1]和∀t∈(R,t0)，Ft和Ft0是ℜS-等价的．因证明过程与t0的选取无关，不妨设t0=0．

考虑εn+1有限生成的子模N=J(f)εn+1和．由式（2），若u∈N，则，其中ui(x,t)∈εn+1．由引理1知理想IS是根式理想，则，故N⊂K+μn+1ISN ．从而由Nakayama引理，N⊂K．

于是由假设条件Tf(f◦ℜS)=ISJ(f)可推出

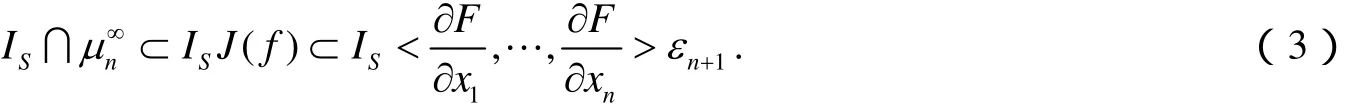
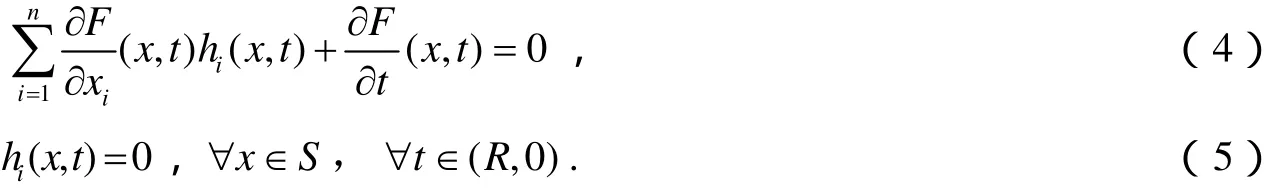
类似地，考虑如下带初始条件的微分方程：

对于任意固定的(n,0) x∈R，由常微分方程基本理论，存在唯一解φ(x,t)满足

将式（4）中的x替换为φ，则有

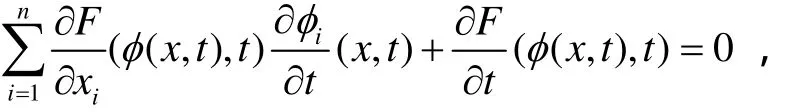
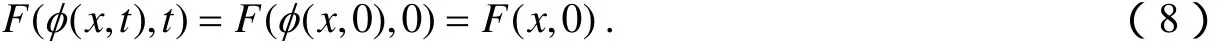
由式（5），显然h(x,t)|S=0,∀t∈(R,0)，于是式（6）的解必满足

令φt(x):=φ(x,t )，则由式（7）、（9）容易推出所得到的芽φt属于ℜS．再由式（8），有Ft◦φt=F0．因而对于t∈(R,0)，Ft与F0是ℜS-等价的．从而证明了∀t0∈［0,1］，存在t0的开邻域Ut0⊂［0,1］，使得对于．由于区间[0,1]是紧的，故必存在φ∈ℜS使得F0◦φ=F1．因此f和g是ℜS-等价的．

证毕.

[1] BARODERSEN H. A note on infinite determinacy of smooth map germs[J]. Bull of London Math Soc, 1981, 13: 397-402.

[2] WALL C T C. Infinite determinacy of equivariant map-germs[J]. Math Ann, 1985, 272: 67-82.

[3] WILSON L C. Infinitely determined map germs [J]. Canada J Math, 1981, 33: 671-684.

[4] WILSON L C. Map germs infinitely determined with respect to right-left equivalence[J]. Pac J Math, 1982, 102: 235-245.

[5] SUN B, WILSON L C. Determinacy of smooth germs with real isolated line singularities[J]. Proc Amer Math Soc, 2001, 192: 2789-2797.

[6] 刘恒兴. 分支问题的无限决定性[J]. 湛江师范学院学报, 1999, 20(2): 1-4.

The Infinite Relative Determinacy of Function Germs

HE Wen-qing, XU Shen-xin
(Insurance Finance Department of Insurance Professional College, Changsha 410114, China)

Infinite determinacy is a way to express the stability of smooth function-germs under flat perturbations. In this paper, we discuss the infinite relative determinacy of smooth function germs with respect to the subgroups ℜSof ℜ, where S is an algebraic set germ in(Rn,0). The result developed the Wilson Theorem.

function germ; algebraic set; infinite determinacy

O189

A

1006-7302（2011）01-0020-03

2010-09-18

贺文青（1982—），男，湖南长沙人，讲师，硕士，研究方向为奇点理论及其应用.