船舶碰撞过程中带板梁结构剪切破坏机理初探
郭 君,朱 枫,崔 杰,姚熊亮
(1.哈尔滨工程大学 船舶工程学院,哈尔滨 150001;2.State Marine Technical University of St.Petersburg,3,Lotsmanskaya Str.,St.Petersburg,190008 Russia;3.中国船舶科学研究中心,江苏 无锡 214082)
近年,船舶碰撞事故频发,所造成的灾害也日益引起人们对船舶安全的重视,美国和欧洲都出台了相应的法律和规划,敦促大型油轮的双壳化[1]。而在学术界,船舶碰撞研究近年来也逐渐成为研究热点,专门的船舶碰撞与搁浅国际会议(ICCGS)也将在赫尔辛基迎来第5届。
若以研究对象划分,可将现有成果划分为如下几类:整船研究,比如附连水质量研究,碰撞外部动力学研究[2];半整船研究,这是指以碰撞区为主要研究对象,远离碰撞区的结构使用某种简化方法代替,这类研究多见于仿真数值领域[3,4];舱段研究,多用于检验、设计和优化目标舱段的耐撞能力[5];板架研究,实验与仿真均比较适合[6];梁研究,几乎是最基础的结构单元,较适合机理研究[7]。本文的研究对象为舷侧纵桁或强肋骨与外板形成的具有高腹板的带板梁,此类结构变形时剪切变形占优,本文对其极限载荷计算、破坏过程中应力分布及其变化过程、吸能成分作了探讨。
1 研究对象
本文的研究对象为长1.2 m的两端刚性固定的带板梁结构,理论计算所用的载荷为跨中对称分布的均布载荷,梁的横截面左右对称。(见图1)。
中和轴与带板中面的距离为z0=9.39 cm,截面惯性矩I=2.12 ×104cm4,翼缘抗弯模量WCP=8.52 ×102cm3,带板的抗弯模量WPP=2.25×103cm3横截面面积ωc=44.5 cm2,翼缘发生屈服时的截面最大弹性弯矩Me=σT·WCP=272.8×103Nm。
带板梁材料特性:弹性模量E=200 GPa,屈服极限σT=320 MPa。

图1 带板梁横截面及载荷示意图Fig.1 Diagram of the cross-section and load of the beam with band plates
2 带板梁极限载荷的理论分析
2.1 变形成分分析
为了研究弯曲变形和剪切变形所占总变形的比例,进行如下推导。
跨中处弯曲挠度为:

跨中处剪切挠度为:
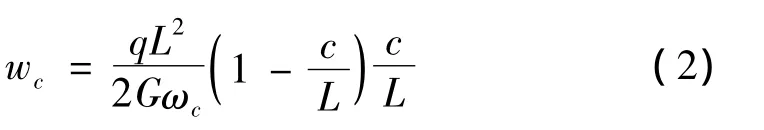
总的挠度为:


k=4.123,我们称之为梁截面系数,主要反映了梁的几何和截面信息;而K=0.9236,称之为载荷系数,主要反映了载荷宽度信息。
2.2 极限载荷分析
根据弯曲变形确定的最大弹性均布载荷和总载荷分别为:

根据剪切应力确定的最大弹性均布载荷和总载荷分别为:
其中,b为腹板厚度,Somc为中和轴一侧截面相对中和轴的静矩,τT为材料剪切屈服极限。

2.2.1 应用表征弯曲破坏模式的极限平衡理论计算梁的极限载荷
该理论[8,9]主要思想为,在极限状态下中和轴位置发生改变,即产生了塑性中和轴,它将梁的截面分成面积相等的受拉和受压的两部分,截面的极限抗弯模量按下式计算:

使梁两端刚性固定处产生塑性铰所需要的均布载荷和总载荷为:
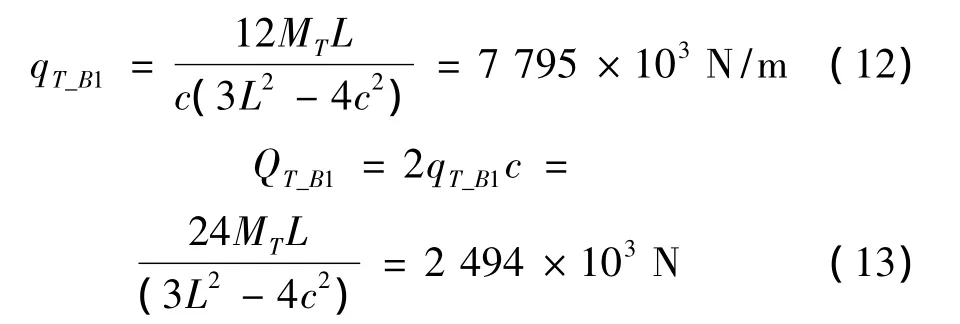
使梁两端刚性固定处和跨中处同时产生产生塑性铰所需要的均布载荷和总载荷为(此时即为弯曲模式的极限载荷)


2.2.2 表征剪切塑性模式的极限状态
梁所能承受的最大剪切力为:

因此极限均布载荷和总载荷为:

各阶段和不同破坏模式的极限载荷和挠度值列于表1。

表1 极限载荷和挠度汇总表Tab.1 Summary of ultimate loadings and deflection
为了验证理论分析的准确性,和更加深入地研究理论分析难以触及的达到极限载荷之后梁的变形和承载特性,将用有限元方法继续分析。
3 极限载荷和达到极限状态后梁的承载特性的有限元分析
3.1 基于ANSYS的极限载荷和剪切应力、变形发展过程分析
在ANSYS有限元分析中带板梁的腹板用壳单元模拟,而翼缘和带板用杆单元模拟,因为二者主要承受拉压应力。有限元网格尺寸限制在20 mm以内,计算中对腹板的变形被限制在腹板平面之内,即不考虑它的失稳(图2)。图3给出了仿真所用的材料特性曲线。仿真将在ANSYS中进行。
求解过程中使用了步进加载的方法,可以跟踪载荷增加引起的响应变化,直到到达载荷极限值。在ANSYS中施加的载荷为与理论计算一样的均布载荷。

图2 带板梁有限元模型(1-带板,2-腹板,3-翼缘)Fig.2 Finite element model of the beam with band plates
得到的载荷、吸能和最大剪切塑性变形曲线见图4。当求解发散时认为载荷已经达到极值,该极值为1655 kN,仅仅与极限平衡理论相差0.8%。此时得到的最大挠度为8.09 mm,远大于理论值1.53mm,这是因为在极限状态,变形量对于载荷的变化已经高度敏感,微小的载荷增加都可能引起很大的变形。从图4(a)可以看到,当载荷为1589 kN时,挠度已经达到2.04 mm,而挠度为理论极限值1.53 mm时,对应的载荷为1420 kN,小于理论值14%。
吸能曲线呈现了双线性特征,在挠度从0 mm到1 mm的区间内,载荷随挠度增加快速上升,此时吸能曲线应是一条二次曲线,只是挠度区间很窄,近似看成线性的;另一条斜率较大的直线在挠度1 mm~8 mm区间,此时结构逐渐进入塑性阶段,载荷增加很小,可近似看成常数,吸能曲线为线性(图4(b))。
图5给出了合成应力、正应力和剪应力随着载荷增加的分布变化。
最大合成应力首先出现在带板加载区域的边缘(图5(a));然后高应力值向腹板深处扩展到中和轴附近(图5(b));最后在极限载荷作用时,除了均布载荷施加处的正下方,其余整个腹板全部处于高合成应力区(342 MPa~370 MPa)(图5(c))。


轴向的最大拉应力首先在跨中翼缘附近,而最大压应力则分布在刚性固定端的翼缘附近,而且压应力最大值是拉应力最大值的1.35倍(图5(d))。随着载荷继续增加,该比值发生变化,到极限载荷1655 kN时,其值为0.91。此时最大压应力值已从固定端转移至跨中载荷施加处的带板附近(图5(f))。
而剪应力最大值在加载初期分布在带板载荷施加处的边缘(图5(g));然后和合成应力类似,高剪应力区也向中和轴附近移动(图5(h));最后达到极限载荷时,除了均布载荷施加处的正下方,其余整个腹板全部处于高剪应力区(144 MPa-185 MPa)(图5(i))。

图5 应力分布汇总结果Fig.5 Summary results of stress distribution
为了更加清晰地观察剪应力τxy随载荷大小及梁长度方向不同位置的变化,图6给出了在5个大小不同载荷作用下(0.6,0.7,0.8,0.9,1.0)×1.655 MN,在沿梁长度方向上的4个横截面上,剪应力沿腹板高度方向上的分布情况。在极限载荷1.655 MN作用时,所有的选取的横截面剪应力均达到了自己的极限值184.6 MPa(即)。

图6 剪应力沿腹板高度方向的分布(图中每条曲线对应一个载荷,从左至右分别为0.993 MN,1.158 MN,1.324 MN,1.490 MN,1.655 MN)Fig.6 Distribution of shear stress along web height
中和轴上的剪切塑性变形的随载荷增加的发展过程(见图7)。首先剪切塑性变形发生在加载区域的边缘,然后逐渐向两边的刚性固定端扩展,而达到极限载荷时最大剪切塑性变形为3.1%,并且依然位于加载区域的边界处。

图7 整个梁长度方向上中和轴上的剪切塑性变形分布Fig.7 Distribution of shear plastic deformation at neutral axis along the beam direction
3.2 基于LS-DYNA的带板梁碰撞破坏分析
在实际的碰撞过程中,带板梁所受的来自撞击物的载荷虽然也应是分布式载荷,但很难是均布的。为了更加准确地模拟带板梁受撞击直至破坏的过程,载荷从均布载荷换成撞击物,利用LS-DYNA的接触功能实现梁的加载。
刚性撞击物速度恒定为10 m/s,撞击接触的区域与理论计算的均布载荷区域大小和位置一致。带板梁结构用体单元模拟,而刚性撞击物用壳单元模拟,所有单元最大尺寸不超过17.5 mm。边界条件依然为梁两端刚性固定,与ANSYS不同的是允许腹板失稳。梁材料特性如前所述。
梁在受撞击变形过程中的关键情景在图9中给出。由于大的塑性变形在腹板上出现了褶皱状失稳,而断裂最先发生在撞击接触区的带板边缘,这与图7中隐式静态分析得到了一致的结果。断裂时的挠度为179 mm,为腹板高度的52%。


图10给出了接触力和吸能随挠度变化的曲线。撞击中接触力最大值变化范围大致为1300 kN~2200 kN,均值1760 kN,大于理论预测值7.2%。应该指出,无论理论预测还是ANSYS中的静力分析,所涉及的挠度都在10 mm内的微小区间,远远低于梁实际破坏时的挠度,梁在大挠度时轴向力和变形显然是不能够被忽略的,正因如此,LS-DYNA的最大载荷结果远大于其它两种方法,表2给出了上述三种方法的计算结果。关于轴向力的影响分析将在下面的吸能分析中进行。结构吸能与最大挠度可认为是线性关系(图10(b))。

图10 LS-DYNA给出的带板梁撞击计算结果Fig.10 LS-DYNA results of the beam with band plates collision

表2 各种方法计算的极限载荷及其对应挠度的对比Tab.2 Contrast of ultimate loadings and deflection calculated from different methods
4 带板梁受撞吸能的成分分析
吸能的成分应包含弯曲能、剪切能和轴向变形引起的膜应变能。在计算吸能成分时,认为剪切极限状态从挠度为零开始到腹板失稳结束,腹板失稳后能量吸收仅由膜应变完成。做这样的假设是基于如下考虑:
第一,极限承载状态之前的挠度相对破坏时的挠度很小;另外,失稳之后完全不计剪切能的贡献所引起的误差可由忽略掉的这部分剪切能做某种补偿。
第二,从仿真结果观察到,腹板失稳之后,仅仅带板完全随着撞击物在移动,而翼缘和大部分的腹板垂向位移很小(图11)。显然,带板的变形完全可认为是膜应变,即便是仍然随着撞击物运动的部分失稳腹板,其变形也应主要为膜应变。

图11 带板梁吸能成分计算Fig.11 Energy-absorbing composition of the beam with band plates
相应的计算公式为:
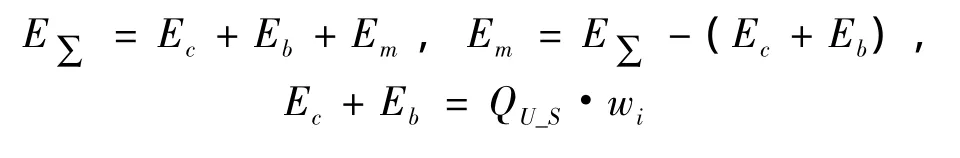
这里E∑-挠度为wi时梁的总吸能;Ec-剪切能;Eb-弯曲能;Em-膜应变能。
E∑从LS-DYNA的结果可直接获得,(Ec+Eb)由理论分析获得的各阶段的载荷对挠度积分获得:。吸能成分计算结果见图12,随着挠度的增长膜应变能从零开始增加,特别是在腹板失稳之后(挠度59.6 mm),它的增加很快,并且最终在梁破坏时(179 mm)超过了弯曲能和剪切能之和达到总吸能的60.6%。

图12 吸能成分随挠度变化曲线Fig.12 Curve of energy-absorbing composition versus deflection
5 结论
(1)对本文所研究的带板梁,根据剪切应力所确定的极限载荷远小于弯曲应力确定的极限载荷,并且比弯曲应力确定的最大弹性载荷还小13%,因此可以确定该梁的基础塑性变形为剪切变形。
(2)极限平衡理论所计算的极限载荷与ANSYS中均布载荷静力分析得到的极限载荷接近,略小于LSDYNA中撞击动力分析得到的大变形条件下的最大载荷。
(3)发生腹板失稳之后,剪切变形对吸能的影响迅速下降,膜应变能逐渐上升为主导吸能方式。
[1]胡志强,崔维成.船舶碰撞机理与耐撞性结构设计研究综述[J].船舶力学,2005,2,131 -142.
[2]Pedersen P T,Zhang S M.On impact mechanics in ship collosions[J].Marine Strucntures,1998,11:429 -449.
[3]王自力,顾永宁.船舶碰撞数值仿真的一种组合模型[J].华东船舶工业学院学报,2001,6:1-6.
[4]王自力,蒋志勇,顾永宁.船舶碰撞数值仿真的附加质量模型[J].爆炸与冲击,2002,4:321-326.
[5]Ozguc O,Das P K,Barltrop N.A comparative study on the structural integrity of single and double side skin bulk carriers under collision damage[J].Marine Strucntures,2005,18:511-547.
[6]朱新阳,吴 梵.加筋板在横向撞击下的吸能特性研究[J].海军工程大学学报,2008,3:25 -30.
[7]刘敬喜,叶文兵,胡紫剑.单壳船舷侧结构的碰撞分析[J].中国造船,2008,49:124 -133.
[8]Малинин Н.Н. Прикладная теория пластичности и ползучести.[М].Машиностроение,1975.

