索牵引并联机器人中变长度柔索的动力学分析

杜敬利，保 宏，宗亚雳，崔传贞

(西安电子科技大学 电子装备结构教育部重点实验室，西安 710071)

正在筹建的500 m大射电望远镜中的索支撑系统是一典型的6索牵引并联机器人，由6根大跨度柔索拖动装有精调机构的馈源舱体实现空间扫描运动［1］，如图 1 所示。

索牵引并联机器人结合了并联机构和柔索驱动的特点，已形成比较完整的体系。文献［2］研究了索牵引并联机器人的工作空间，并给出了一种求解工作空间边界的解析方法。文献［3］采用神经网络复合策略研究了索牵引并联机器人的正解问题。文献［4］建立了一种6自由度索牵引并联机器人的动力学模型，采用反馈线性化+PD控制的方法研究了其轨迹跟踪问题。文献［5］探讨了7索牵引时的索张力优化与控制问题，利用非线性前馈+PD控制来实现系统的运动控制。以上研究中，由于系统的工作空间较小，均将柔索简单地处理成仅能承受张力的索杆单元，没有考虑柔索弹性变形、自身振动等力学特性。

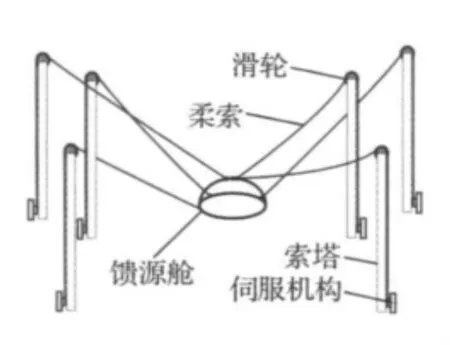
图1 索支撑系统示意图Fig.1 Schematic of the cable-supporting system

对于大射电望远镜的索支撑系统，由于柔索跨度巨大且运行精度要求较高，力学分析时文献［1，6，7］均认为必须考虑柔索垂度的影响，但因系统运动缓慢，可忽略柔索的动态特性，基于静力学模型进行运动控制。

从已有文献来看，现阶段研究中，当系统的工作空间较小，柔索的垂度可忽略不计时，均采用索杆单元来模拟柔索;当柔索跨度较大必须考虑垂度影响，且系统运动缓慢时，则忽略其动态特性而采用静态悬链线对柔索建模。但当柔索跨度较大，运行精度要求较高时，能够考虑到柔索自身动态特性影响的索牵引并联机器人动力学模型却尚未见刊载。

柔索本身的柔性较大，系统运行过程中必然导致动态运动轨迹偏离其静平衡位置。同时因为索牵引并联机器人的刚度较小，即使索长变化非常缓慢，甚至保持不变时，在外界扰动作用下末端执行器也会出现绕其平衡位置的振动。随着对索牵引并联机器人运行精度和速度要求的不断提高，研究更为精确的、适用于时变索长的动力学模型具有重要的现实意义。本文的目的是对索长缓慢变化时的索牵引并联机器人的动力学特性进行探讨，此时可将其视为一个平衡位置不断变化的结构振动问题。

本文将结合大射电望远镜的索支撑系统，对其精确动力学建模问题进行研究。文中首先建立了变长度柔索的偏微分动力学方程，并采用中心差分法进行求解。然后，根据柔索与末端执行器之间的动力学耦合关系得到索牵引并联机器人的动力学模型。最后，给出两个数值算例来证明本文模型的有效性。

1 变长度柔索的动力学分析

索支撑系统中的任一柔索j(j=1，2，…，6)，从执行机构输出后绕过定滑轮与末端执行器相连，见图1。为简洁起见，本节推导中省略了柔索的下标j。以柔索的无应变状态为参考，对于长度为L的柔索，设其上任一点P距原点的曲线坐标为s∈［0，L］，受力后对应的长度为se。这样柔索的轴向应变可表示为:

柔索应满足的几何约束为:

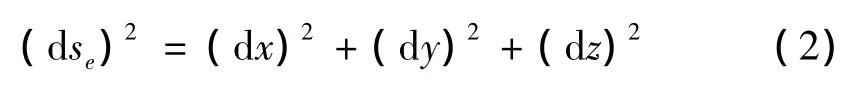
式(2)两边同除以 d s，并将式(1)代入，得(1+ε)2=，略去二次小项后有［8，9］:

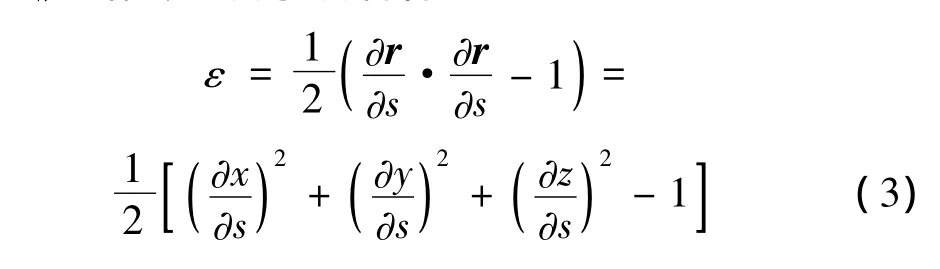
在任意时刻 t，设点 P对应的位置矢量为 r(x，t):［t0，∞)×［0，L］→R3，且柔索在该处的切线方向为:

其中，r(s，t)=［x(s，t)，y(s，t)，z(s，t)］T。

于是，柔索的动力学方程可以表示为:

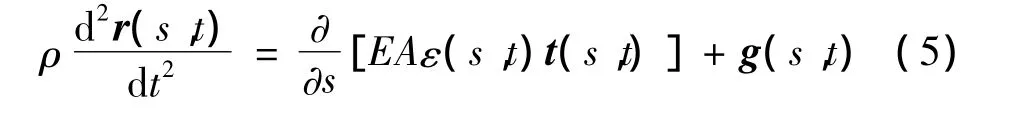
式中，ρ为柔索单位无应变长度的重量，ε(s，t)为柔索的应变，EA为柔索的抗拉刚度，g(s，t)为柔索单位无应变长度上的外力，本文中仅考虑柔索自重的影响。

柔索上曲线坐标为s处点P的速度为:

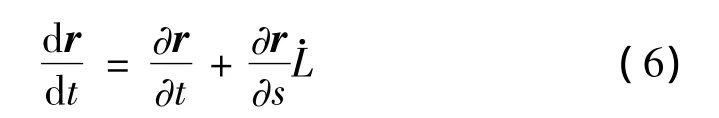
加速度为:

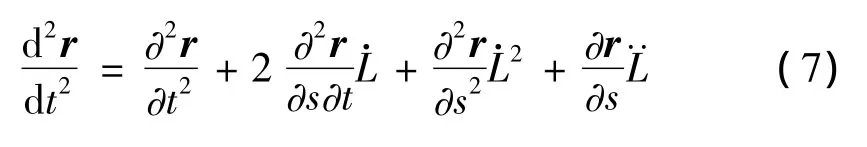
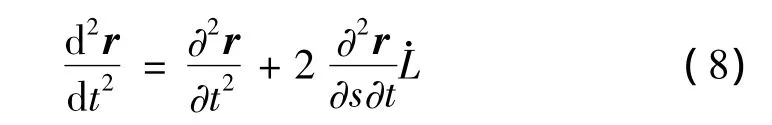
将式(3)、式(4)和式(8)代入式(5)即为柔索的动力学方程，为一关于s和t的偏微分方程。

2 动力学模型的空间离散化求解

采用有限差分法对式(5)进行空间离散化，每根柔索均划分为n个等长单元，见图2，有:l=L(t)/n (9)其中，L(t)为柔索当前时刻的无应变长度。

图2 柔索的空间离散化Fig.2 Spatial discretization of a cable

采用中心差分法，柔索上曲线坐标为si的第i(i=1，2，…，n－1)个节点的x分量关于s的一阶和二阶偏微分可分别表示为:

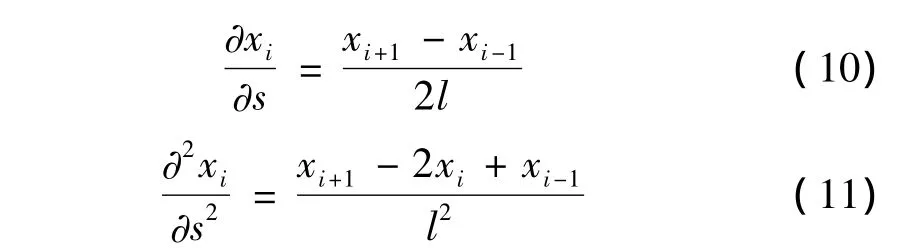
于是，第i个节点沿x方向的速度和加速度分别为:

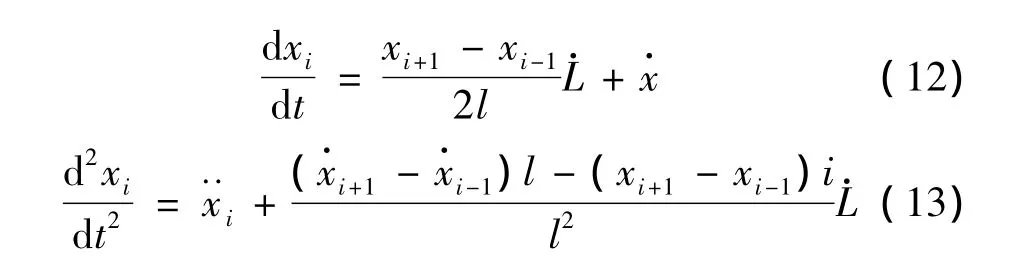
同理，可得节点i沿y轴和z轴的加速度。将相关各式代入式(5)得:

式中，pix(xi－1，…，zi+1)为柔索内力项，是节点坐标xi－1，…， zi+1的非线性函数，gix为重力项沿x方向的分量，分别对应于式(5)右边的第一项和第二项。限于篇幅有限，不再给出pix的具体表达式。

柔索沿y和z方向的动力学方程与式(14)类似。于是，第i个节点的动力学方程可以写成如下形式:

其中:

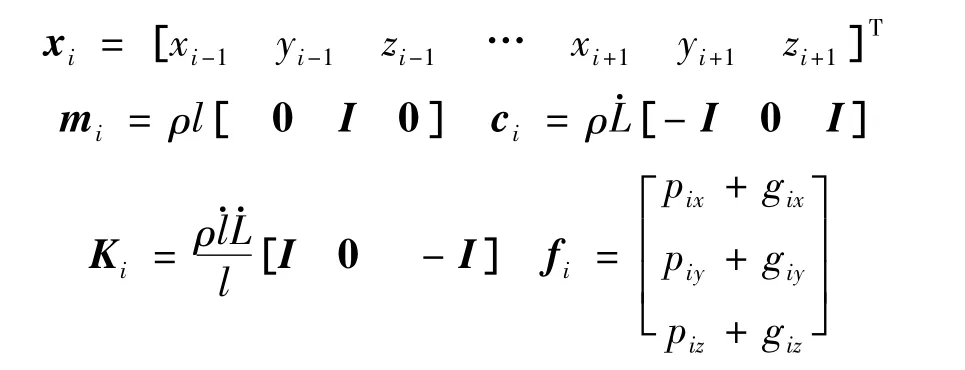
这里，I和0分别为3×3阶单位阵和0矩阵。对于整根柔索，记:

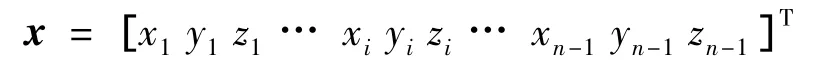
采用有限元装配操作对式(15)中的矩阵mi、ci、ki和fi进行装配操作得到相应的全局矩阵mc、cc、kc和fc。于是可得变长度单根柔索的动力学方程为:

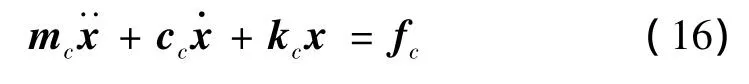
这是一个共3(n—1)个变量的二阶微分方程组。需要指出的是，这里fc为节点等效力向量，cc和kc是与索长收放速度相关的系数矩阵，不同于普通有限元中的阻尼阵和刚度阵。普通有限元中的阻尼项和刚度项体现在式(16)右端的等效力向量fc中。

3 索牵引机器人的动力学模型

在末端执行器上建立与其固连的局部坐标系{B}，将末端执行器位置和姿态坐标取为:

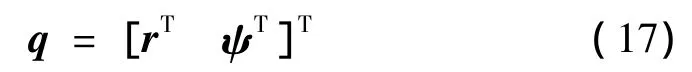
其中，r=［x y z］T为末端执行器的位置向量，ψ=［α β γ］T为姿态向量。

柔索作用在末端执行器上的合力fr和合力矩mr可分别表示为:

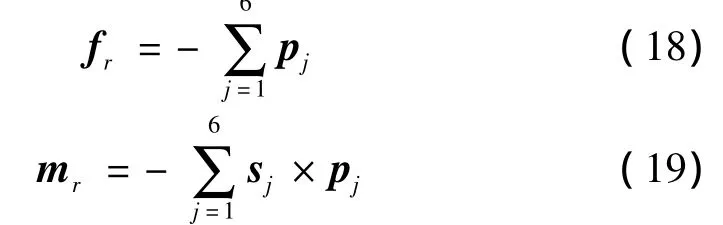
其中，pj为第j(j=1，2，…，6)根柔索对末端执行器的牵引力。

末端执行器的动力学方程可以表示为［10］:

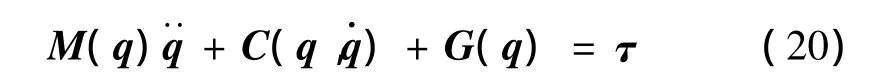
柔索连接末端执行器的6个索连接点在其局部坐标系{B}中的位置向量记为bj(j=1，2，…，6)。将其转换到全局坐标系中，有:

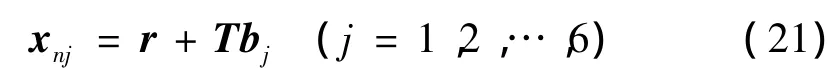
其中T为从局部坐标系{B}到全局坐标系的坐标变换矩阵，可由末端执行器的姿态向量ψ确定。xnj为式(16)求解时第j根柔索的末端节点n的当前位置。

式(16)、式(20)与式(21)联立即为索牵引并联机器人的动力学模型。

4 索牵引并联机器人数值算例

针对本文提出的时变索长索牵引并联机器人动力学模型，首先给出一平面两索牵引并联机构的算例，并与多体系统动力学分析软件DADS的分析结果进行对比来验证本文算法的有效性，然后再给出6索牵引并联机器人的分析结果。

4.1 平面两索牵引并联机构

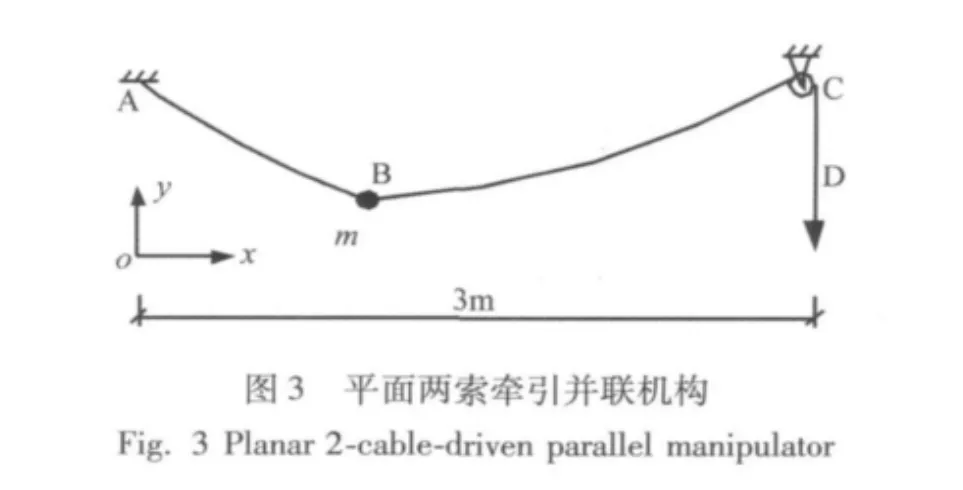
图3所示的平面两索牵引并联机构中，柔索AB与BC共同牵引B点处的质量m进行平面运动。柔索AB的A端固定不动，柔索BC的C端绕过定滑轮后在点D处施加运动即可改变BC段的长度，从而拖动质量m运动。各点位置坐标为 A(– 1.0，1.0)，C(2.0，1.0)，(单位 m，下同)。初始平衡时 B点坐标为(0.00177，0.50529)。柔索抗拉刚度 EA=6.5973 ×104N，单位长度重量 ρ=2.0 N/m，质量 m=1.37kg。此处ρ值取得较大而EA和质量m的值较小是为了能够突出柔索自身动态特性对质量m运动的影响。

需要指出的是，点C为系统处于初始平衡状态时，柔索BC与定滑轮的切点，采用本文算法时认为该点固定不动。仿真时柔索AB划分为7个单元，BC划分为10个单元。

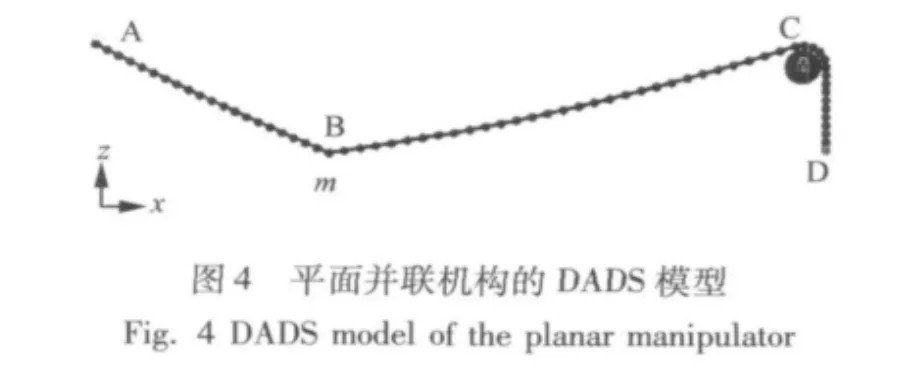
为了验证模型的正确性，对图3所示机构采用DADS软件建立了如图4所示的弹簧－质量系统来模拟两索牵引并联机构的动力学行为。在点D处施加位移驱动以改变柔索BC段的长度，每个质量点用一刚性小球来表示，小球与滑轮间处理为接触，用DADS的接触副建模，滑轮半径为0.08 m。

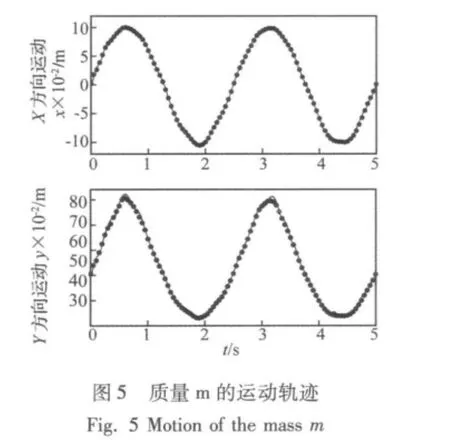
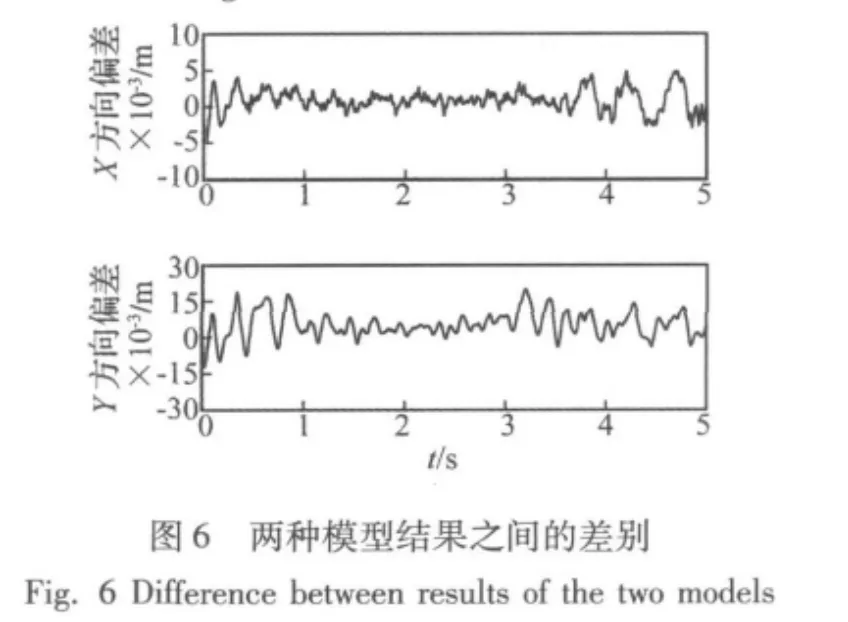
柔索AB长度不变，柔索BC端点D处的收放规律为 ΔL(t)=0.15sin(0.8πt)，仿真时间为 5 s。此时，质量m沿x轴和y轴的运动规律如图5所示。图5中，实线为本文算法结果，圆点(·)为DADS仿真结果。图6给出了本文结果相对于DADS结果之间的差别。由图5和图6可知，质量点在x方向的运动幅度约为0.10 m，两种模型之间的差别在5 mm以内;y方向的运动幅度约为0.30 m，相应的差别在15 mm内。可以看出，本文结果与DADS仿真结果之间吻合得很好，由此可以证明本文提出的柔索动力学模型是非常有效的。考虑到DADS模型中切点C的位置是略有变化的，两模型间存在一些差别，仿真结果稍有不同也是合理的。

应当指出的是，为了保证柔索与滑轮之间连续且光滑接触，两质量点间的距离应小于滑轮半径。为此，将柔索BC划分为30个弹簧－质量元。由于工程应用中滑轮半径远远小于柔索长度，采用DADS软件分析时必须将柔索划分成大量的弹簧－质量元。同时采用接触副时求解步长必须足够小。因此，与本文提出的求解模型相比，采用DADS软件分析时由于引入柔索节点与滑轮间的接触，求解过程是非常耗时，而且使用接触容易出现数值计算上的失败，极大限制了这种方法的应用。

4.2 6索牵引并联机器人

图1所示的大射电望远镜索支撑系统中，6个塔顶定滑轮的高度均为21 m，均匀分布在直径为50 m的圆上。柔索抗拉刚度EA=2.39×106N，单位长度重量ρ=1.37 N/m。作为末端执行器的半球壳形馈源舱体半径为 0.50 m，质量为 400kg，惯量矩阵为 diag(33.97，33.97，54.34)(kg·m2)，这里 diag表示对角阵。6个索连接点均位于舱体表面上，其中3个距舱底面的高度为0.10 m，另外3个的高度为0.48 m。空间离散化时每根柔索划分为20个单元。

给定末端执行器初始位姿为 q0=(2.00，1.00，16.0，0.0889，－ 0.1756，3.108)T，其中长度单位为m，角度单位为rad，下同。要求末端执行器在10 s内沿直线轨迹运动到终点 q1=(2.50，1.50，16.2，0.135，－0.263，3.121)T，运动过程中每个坐标分量的轨迹均为直线。文［1，6］认为由于运动缓慢，在轨迹上任一点处系统均处于静平衡状态。本文将这种运动称为静态运动。

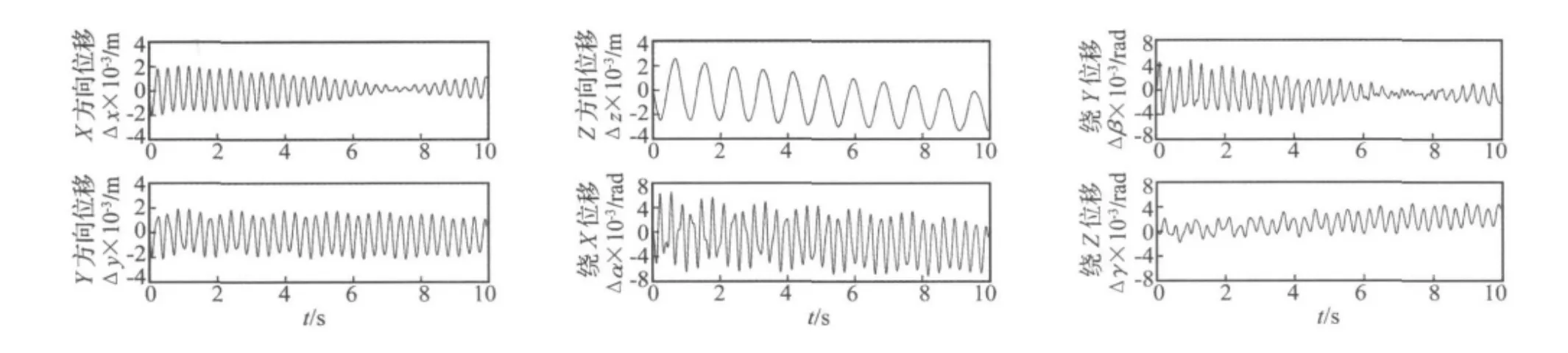
图7 末端执行器的动态位移Fig.7 Dynamic displacement of end-effector

本文模型结果相对于静态运动的位移偏差如图7所示。可以看出，系统运动过程中会出现围绕其静平衡位置的振动。振动导致的总体位置误差((Δx2+Δy2+Δz2)1/2)为3.5 mm，总体姿态误差为 8.25 ×10–3rad(0.47°)。由此可见，在理想情况下，文献［1，6］认为系统处于静平衡状态是合理的。

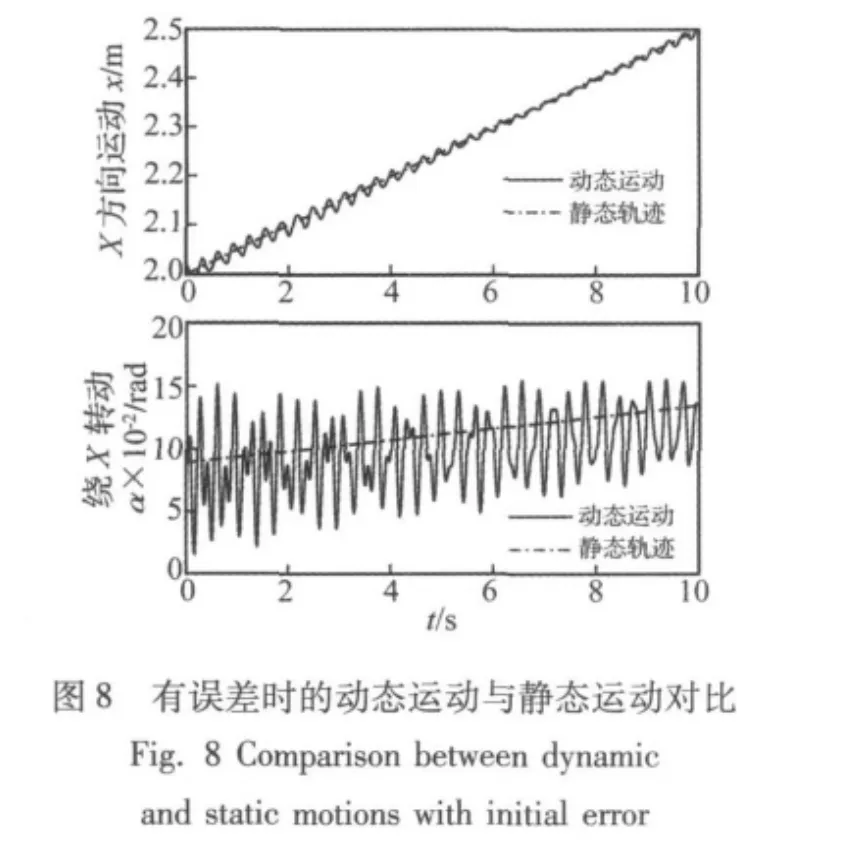
但当系统中存在误差时，柔索动态特性的影响会显著增加。例如，由于设备的测量误差，导致给定的末端执行器初始位置沿3个坐标轴方向各有20 mm的位置误差时，系统沿x轴平动和绕x轴转动的运动轨迹如图8所示，相对于静态运动的位移偏差在图9中给出。可以看到，初始误差导致的振动始终存在，沿x轴的平动振幅接近于20 mm;绕x轴的转动振幅接近6.0×10–2rad(3.4°)。其他方向上的运动与此类似。此时，振动导致的总体位置误差为32 mm，总体姿态误差为8.2 ×10–2rad(4.7°)。而且，运动过程中振幅衰减很慢，这是由于柔索系统的阻尼很小造成的。

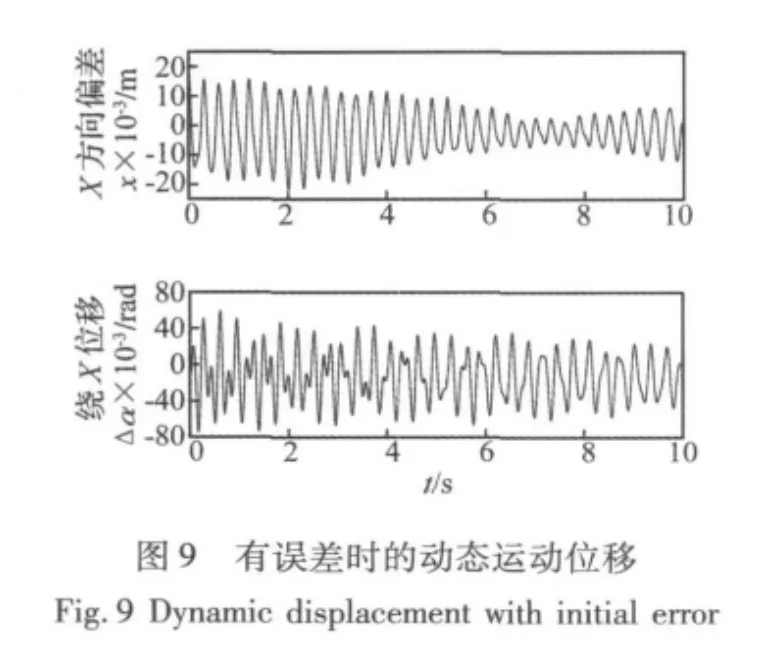
计算中发现，系统的运动速度增大时，动态特性的影响也会相应增大，导致动态运动轨迹远离其静平衡位置。因此，当系统的运动速度较大或运动精度要求较高时，考虑柔索动态特性的影响是必要的。

5 结束语

本文首先推导了索长慢速变化时柔索的动力学方程，在此基础上根据柔索与末端执行器之间的耦合关系推导出索长变化时索牵引机器人的时变结构动力学模型，为评估柔索动态特性对末端执行器定位精度的影响提供了参考。

计算过程中发现，当柔索长度变化很慢时，含索长变化速度L·(t)的相关各项均可忽略不计。此时系统转变为一个平衡位置不断变化的结构振动问题。工程中对柔索进行动力学分析时大多只需考虑其前一、二阶振动模态的影响，因此，仅需将柔索划分为少数几个单元就可以很好地考虑到这些模态的影响。

随着索长收放速度的加快，末端执行器偏离其静态平衡位置的程度越来越大，系统的非线性动力学特性更加复杂。此时分析时必须依据不同索长及索长收放速度，采用不同的建模方法。控制器的设计与系统的动力学模型直接相关。只有多方面因素综合考虑，才能精确控制其未端执行器的定位精度。

应当指出的是，根据不同的索长变化速度来确定与索长变化速度和加速度相关各项的取舍以及柔索划分单元数目的合理确定仍是需要进一步讨论的一个重要问题。

［1］Duan B Y，Qiu Y Y，Zhang F S，et al.On design and experiment of the feed cable-suspended structure for super antenna［J］.Mechatronics，2009，19(4):503 －509.

［2］Bosscher P，Riechel A T，Ebert-Uphoff I.Wrench-feasible workspace generation for cable-driven robots［J］.IEEE Transactions on Robotics，2006，22(5):890 －902.

［3］Parikh P J，Lam S S.A Hybrid strategy to solve the forward kinematics problem in parallel manipulators［J］.IEEE Transactions on Robotics，2005，21(1):18－25.

［4］Oh S R，Agrawal S K.A reference governor based controller for a cable robot under input constraints［J］.IEEE Transactions on Control Systems Technology，2005，13(4):639－645.

［5］Fang S，Franitza D，Torlo M，et al.Motion control of a tension-based parallel manipulator using optimal tension distribution［J］.IEEE/ASME Transactions on Mechatronics，2004，9(3):561－567.

［6］Kozak K，Zhou Q，Wang J.Static analysis of cable-driven manipulators with non-negligible cable mass.IEEE Transaction on Robotics，2006，22(3):425 －433.

［7］杜敬利，段宝岩，保 宏，等.一种缓慢运动索牵引并联机器人的跟踪控制［J］.振动与冲击，2008，27(11):173－176.

［8］Ni Y Q，Lou W J，Ko J M.A hybrid pseudo-force/laplace ransform method for non-linear transient response of a suspended cable［J］.Journal of Sound and Vibration，2000，238(2):189－214.

［9］金栋平，文 浩，胡海岩.绳索系统的建模、动力学和控制［J］.力学进展，2004，34(3):304 －313.

［10］訾 斌，段宝岩，杜敬利.柔索驱动并联机器人动力学建模与数值仿真［J］.机械工程学报，2007，43(11):82－88.