电磁阀试验台的流体脉动及其消减措施的研究
郭北涛 ,柳洪义
(1.东北大学 机械工程与自动化学院,沈阳 110004;2.沈阳化工大学,沈阳 110142)
传统的电磁阀综合性能检测劳动强度大、效率和测试精度都较低,本课题是与中国电磁阀国家标准起草单位共同研制合作开发的电磁阀自动化检测试验台。该试验台可实现电磁阀综合性能的各项自动化检测试验,可大大提高检测精度和效率并降低检测成本,并被应用于实际生产检测以及新产品研发测试中。因此该试验台的开发对推动合作企业电磁阀的生产乃至电磁阀行业的发展都起着重要的作用。因泵源脉动和阀门启闭等因素造成流体压力冲击和脉动诱发的谐振会对电磁阀试验台的正常工作带来非常不利的影响:轻者会降低效率、增加能耗、缩短元件寿命和使高精度传感器失灵,致使检测工作精度无法保证;重者会因振动和噪声使流体管路或容器的联结部位发生松动或破裂而酿成事故。因此,本文的研究内容主要包括分析诱发电磁阀试验台流体脉动和冲击的机理并对流体系统尤其是主测试管路的谐振特性进行研究。在此研究基础上采取合理的消振和滤波措施,从而有效地衰减流体脉动和冲击引起的谐振对电磁阀试验台流体系统和主测试管路的影响[1]。
1 电磁阀试验台流体系统脉动源分析
因电磁阀试验台用于实际生产检测以及新产品研发测试,每天需测试大量电磁阀并对其进行各项性能试验,因此具有频繁使用且间歇动作的特性,使管路内流体经常以非恒定流状态频繁振荡。因各主测试管路均刚性固定在流体试验台架上,故只讨论由于非恒定流动诱发流体冲击和脉动导致的谐振。首先探讨引起电磁阀试验台流体系统产生脉动的脉动源,并对引起主测试管路发生谐振的主激振源进行了重点分析。
1.1 脉动源
容积式液压泵的工作原理是密闭的工作容积发生周期性变化,完成吸油和排油过程,因此造成其瞬时流量脉动从而形成液压泵出口流量的脉动。对于电磁阀试验台来说泵源脉动对系统的影响最大,当泵源脉动的脉动频率与主测试管路的固有频率一致或接近时,将会出现振幅不稳定的共振现象,使系统在刚启动管路通流时即无法工作,更无法保证后续测试工作的顺利进行。因此,泵源的脉动对电磁阀试验台的振动影响最大,故将其作为主激振源重点加以分析[2]。
(2)液压管路中因液流方向改变产生的压力脉动
当方向控制阀或执行元件在迅速停止、变速或换向时,管道内液流的流速或方向将会改变,但由于惯性的作用仍保持原有的运动状态则会使压力突增,并一层层沿系统反方向传播,而且又遇到液压泵输出的压力脉动,从而使管道内的压力升高,产生大的压力脉动[3]。
电磁阀的动作试验、响应时间试验和寿命试验均依靠被测电磁阀的多次启闭动作完成,这将会带来不可避免的压力冲击和脉动。但流体在运动过程中因为流体的粘性摩擦和流体及管壁的变形作用,能量不断损失,因而压力冲击波在管道中的传播并不是一个振幅不变的持续振荡,而是不断快速衰减并最终消失的振荡。可通过人为加以控制即设置阀动作节奏的快慢和加装蓄能器组等措施最大程度的消减因压力冲击波对试验台流体系统的影响[4]。
(3)液压控制阀产生压力脉动
基坑与斜拱桩基承台边缘净距不同时,斜拱桩基产生的水平推力对深基坑的影响是不同的。分析边缘净距L对邻近深基坑围护桩的影响时,斜拱桩基先于深基坑施工,即基坑开挖前斜拱已经对承台施加荷载。边缘净距L分别取为5 m、10 m、15 m、20 m、25 m、30 m。图6和图7分别为不同边缘净距下围护桩桩身最大水平位移分布图和围护桩最大水平位移变化曲线图。
引起液压阀阀口处压力脉动的主要因素是阀芯位移x、固有频率ωn和弹簧刚度k等。在有源压力脉动激励下,如果弹簧刚度变低(如弹簧折断或变软),该阀固有频率将降低并产生激励振动。此外,如果阀芯处关闭不严将会产生泄漏,使流体产生低频率和低幅值的压力脉动。因此,应定期对试验台液压控制阀进行检修和维护使其处于正常运行状态[5]。
1.2 主激振源激振频率的计算
凡利用容积变化原理工作的泵源,如柱塞泵、齿轮泵等,其输出的瞬时流量均可用周期函数来描述。也可认为瞬时流量是在泵的直流流量上叠加高频脉动流量而成。当高频脉动流量遇到液压系统管路的阻抗时又形成压力脉动。奇数柱塞泵产生的流量脉动要比偶数柱塞泵小很多,考虑到泵源是产生压力和流量脉动的主要因素之一,为了减少流量固有脉动生产上优先选择奇数柱塞泵。其中,奇数柱塞泵脉动频率公式为:f=nZ/30。
电磁阀试验台选用的泵为奇数7柱塞泵,转速为1000 r/min ~1600 r/min,额定转速为 1250 r/min,按照上述分析计算得流量脉动频率范围为233.3 Hz~373.3 Hz,额定频率为 291.7 Hz。
2 主测试管路的频率特性研究和消减脉动措施
引起谐振的另一因素也就是系统阻抗。如果系统阻抗满足谐振条件,即使振动源的干扰很小也会在流体系统内产生谐振,引起流体压力或流量的剧烈振荡。采用调整系统阻抗的方法也就是调整流体系统的谐振点以避开振动源流量或压力脉动的主频率,从而避免发生谐振。所以在设计试验台流体系统时要先对系统进行阻抗计算后再选取最佳的结构和元件参数,可有效地减少和消除流体系统可能出现的压力脉动并避开谐振现象的发生[6]。
2.1 流体传输管道动态特性的基本方程
当一个瞬变或脉冲压力信号在管内传递时,由于管道分布参数效应,将会使信号产生时延,随频率增加的相移、信号幅值放大或衰减和波形畸变等现象。通过与电传输线模型进行类比,可以得到流体传输管道动态特性的基本方程如式(1)所示[7]:
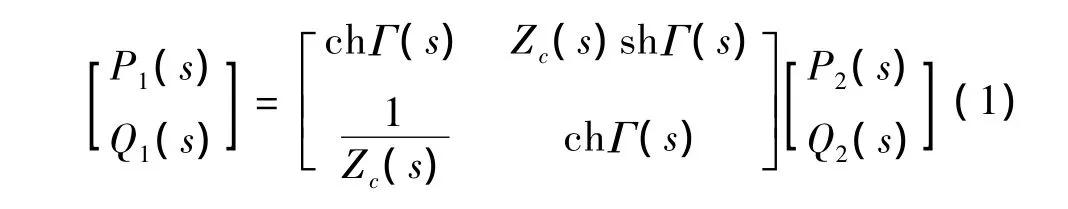
其中:P1(s)、Q1(s)和P2(s)、Q2(s)分别为管道入口和出口压力、流量;Γ(s)=γ(s)l为传播算子;Zc(s)=为特征阻抗;γ(s)=为传播常数;Z(s)为串联阻抗;Y(s)为并联导纳。
2.2 主测试管路频率特性的研究
频率特性分析法是指研究流体管道内的非恒定流即流体管道的动态特性时在频率域内对管内流体频率特性进行分析的方法。其主要内容包括对流体管道输入端(源端)和输出端(负载端)的边界元件的压力-流量特性进行分析,得到相应的源阻抗和负载阻抗的表达方法,并据此研究管道系统产生流体谐振的条件以及管道在频率域内的压力传递特性。

图1 流体管道Fig.1 Fluid pipeline
如图1所示的简单管道中,定义其自身的特性阻抗为ZC(s),定义其输入端边界元件输入的压力与流量的比值为源阻抗,即 Zs(s)=;定义管道输出端边界元件为负载,管道输出端压力与流量的比值为负载阻抗,即。源阻抗Zs(s)和负载阻抗ZR(s)的特性主要取决于边界元件的性质,可以是集中参数元件,也可以是分布参数元件,电磁阀试验台主测试管路的输出端负载为电动节流阀,可以简化为节流孔这一常见负载。
管道的压力比频率特性反映了管道输出端压力与输入端压力的频率域内的传递特性,它主要取决于管道的自身阻抗特性和负载阻抗特性。由流体管道动态特性基本方程式(1)可得到管道的压力比频率特性为:
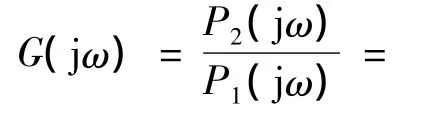

2.3 流体管道的压力比频率特性的算法实现
在式(2)中含有复杂的贝赛尔函数,不易于直接计算,人们一直试图在满足一定精度要求的情况下,采用各种近似表达方法以简化计算。其中,一阶惯性近似模型相比于其它近似计算方法,具有形式简单、适用于整个频率段且为线性近似的特点,便于理论分析,由于当取较少的项数时,浙江大学蔡亦钢博士所得到的一阶惯性近似系数优于其它研究方法选取的系数而起到简化模型的作用,因此本文采用蔡亦钢博士的模型系数[7]。
可以根据以下公式进行计算:
令 Γ(jω)=α +jβ,则:


由一阶惯性近似模型为:
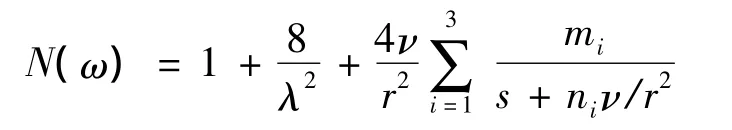
其中mi、ni采用浙江大学蔡亦钢博士的系数取值,即:m1=86.67212;m2=13.3725;m3=4.994301;m4=1.776146;n1=20202.905;n2=1825.3688;n3=257.91872;n4=35.766688;
令 s=jω,可得:
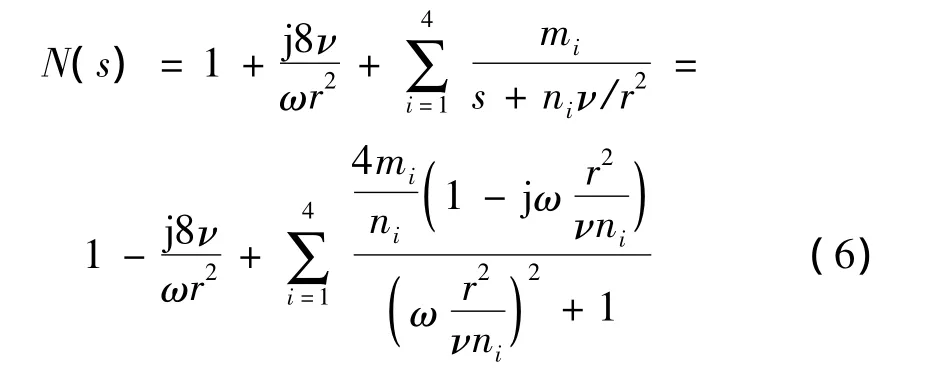
则:
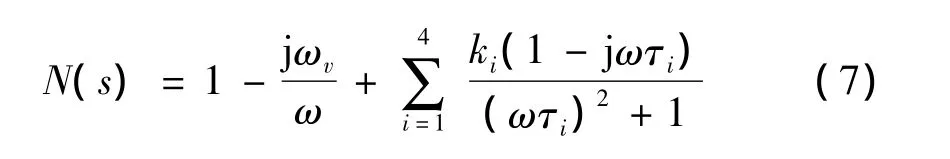
由此可得:

以上推导中所用到的符号定义如下:Γ(jω)为传播算子;γ(jω)为单位长度传播算子;l为管道长度;A为管道横截面积;ν为介质的运动粘度;c0为介质的传播速度;Vc为空腔体积;r为管道半径;ων为粘性频率。
2.4 主测试管路谐振频率的仿真研究
通过仿真研究在计算机上分析与研究实际系统的各种工作状况,确定最佳的控制方案和最佳的参数匹配,加深对系统的了解[8]。本文在MATLAB软件的m文件中编制程序计算主测试管路的压力比频率特性P2/P1,经数学运算将式(2)中的 G(jω)写成 G(jω)=A(ω)ejφ(ω)形式,取对数后可以画出以 20lg A(ω)为纵坐标,以ω为横坐标的对数幅频特性。经仿真得到主测试管路的压力比频率特性如下图所示。
① 通径为10 mm但管路长度不同的主测试管路压力比频率特性仿真曲线的比较:
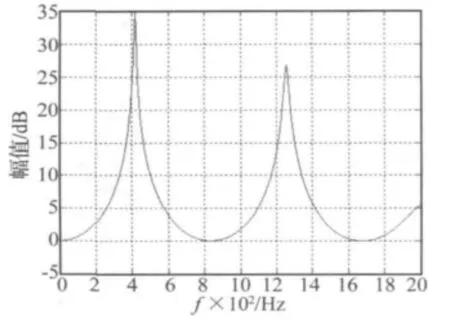
图2 管长4.5 m管路的压力比频率特性Fig.2 The frequency of pressure ratio about the 4.5 m pipeline

图3 管长5.5 m管路的压力比频率特性Fig.3 The frequency of pressure ratio about the 5.5 m pipeline
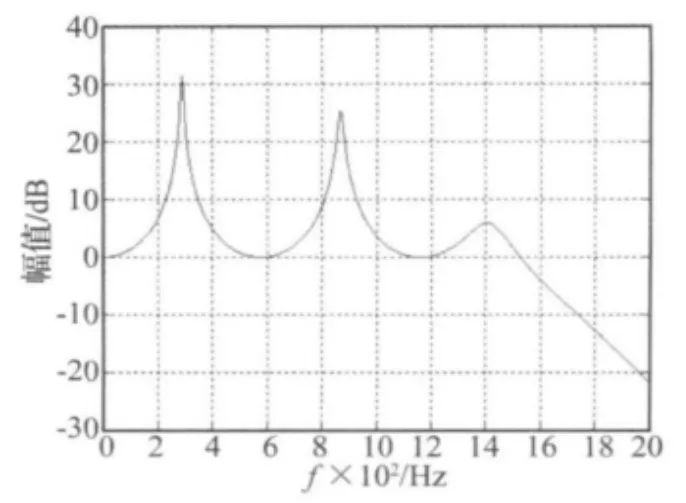
图4 管长6.5 m管路的压力比频率特性Fig.4 The frequency of pressure ratio about the 6.5 m pipeline

图5 管长4.5 m管路的压力比频率特性Fig.5 The frequency of pressure ratio about 4.5 m pipeline

图6 管长5.5 m管路的压力比频率特性Fig.6 The frequency of pressure ratio about5.5 m pipeline

图7 管长6.5 m管路的压力比频率特性Fig.7 The frequency of pressure ratio about6.5 m pipeline
② 通径为25 mm但管路长度不同的主测试管路压力比频率特性仿真曲线的比较:
以上仿真表明:在图2至图4中通径为10 mm的仿真和图5至图7中通径为25 mm的仿真中,管长分别为 4.5 m、5.5 m、6.5 m 的主测试管路发生最大共振的最小频率值随长度的增加逐渐降低。长度相同而通径分别为10 mm和25 mm的主测试管路随着管路直径的增加,发生共振的振幅也增大。
在对泵源作为主激振源的分析中,泵源的脉动频率是以291.7 Hz的倍频传播,故主测试管路发生最大共振处的频率应避开泵源的脉动频率即291.7 Hz及其相近值,由图2至图7的仿真中可知若管长设计为6.5m时则管路的固有频率与泵源脉动频率一致,故管长设计应避开6.5 m及其相近值的长度。
3 其它消减脉动和冲击的措施
通过对脉动源激振频率的分析和主测试管路避免谐振的相关研究,在实际的流体系统中调整系统的阻抗特性(如改变管长和元件结构等)会避免主测试管路的谐振。但采用调整系统的阻抗特性的措施要受到系统合理设计的限制(如系统正常运行工况、元件安装空间方位等),虽将泵源脉动频率和主测试管路发生最大谐振的主频率避开,若二者相差值不是很大时则其距谐振频率附近处的压力幅值仍较大,特别是大通径管路会出现更大压力幅值的可能性,因此,还应采取相关的技术措施:如在设计电磁阀试验台泵站时可根据测试工作条件选择低压大流量齿轮泵和高压小流量柱塞泵的组合,从而避免高压大流量柱塞泵带来的大流量脉动值;在泵源处加入分水缸起到缓冲泵源脉动的作用;考虑到蓄能器作为消振元件是利用介质的压缩性来吸收压力脉动和冲击[9],其作用效果明显且在工程应用上有显著的经济效益,故电磁阀试验台流体系统采用由三只不同参数的蓄能器构成的蓄能器组的措施以有效地衰减或吸收压力脉动和冲击[10]。
4 电磁阀试验台的实验运行
整个电磁阀试验台水流体系统的结构设计是以通径为50 mm和100 mm测试支路居中,10 mm、25 mm测试支路和150 mm、300 mm测试支路分别居于两侧。根据系统结构、各类流体设备尺寸和厂房的布置并结合泵源的脉动频率的分析,为避免谐振发生的主测试管路不同通径支路相应的管长设计如表1所示[11]。进一步结合其它削减冲击和脉动的措施,经现场施工安装完毕后的流体台架如图8所示。选取其中一条测试支路的液压系统原理图如图9所示。
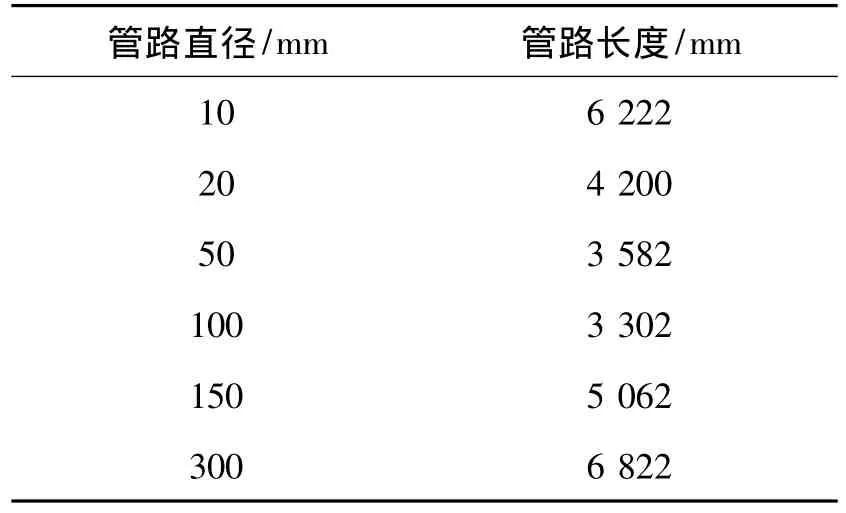
表1 电磁阀试验台主测试管路的参数Tab.1 The parameters of main pipeline for testing in solenoid test-bed

图8 水介质电磁阀试验台Fig.8 Soleoid valve test-bed in water medium
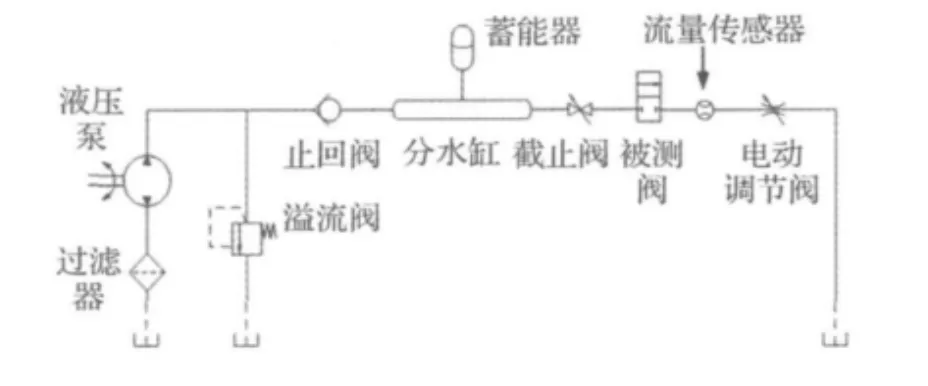
图9 水介质系统试验回路Fig.9 Fluid circuit in the testing system for water medium
电磁阀试验台测试系统采用虚拟仪器软件Labview8.2编程来实现试验系统的监控界面、数据处理、存储与显示以及智能算法等功能。图10中为通径25 mm测试支路开泵通流时在数据采集子程序界面中实时显示地流量、压力曲线及其测量值。可看到压力曲线稳定,没有出现压力剧烈变化而发生管路谐振现象。图11中为进行寿命试验的试验曲线,可看出阀的多次启闭在理论上会带来剧烈的压力冲击和脉动,但因采取相应的削减措施可得到较好的实际测试效果。45(9):1198-1201.

图10 管路通流时的流量和压力曲线Fig.10 The flow and pressure cure as the pipeline flow passage
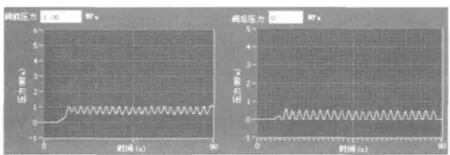
图11 寿命试验曲线Fig.11 The curve of life- span test
5 结论
经理论分析和试验台的实际运行验证说明:在流体试验台的结构设计时对主测试管路谐振特性进行研究是非常必要的;所采取的消减冲击和脉动的相关工程措施是合理的。该电磁阀试验台现已应用于实际生产检测以及新产品研发测试中且运转正常,说明在研发过程中所采用的流体控制理论被成功应用于工程实际项目使得本课题的研究具有一定的理论和工程应用价值,并且普遍适用于相关流体控制和测试系统中。
[1]陈 彬,刘 阁.化工管路系统的耦合振动主动控制研究[J].振动与冲击,200929(8):158-162.
[2]俞继印,金 松,阮 健,等.轴向柱塞泵流量脉动的分析[J].机床与液压,2005,19:22-25.
[3]万五一,练继建,李玉柱.阀门系统的过流特性及其对瞬变过程的影响[J].清华大学学报(自然科学版),2005,
[4]Zhao M,Mohame S.Solutions for water hammer flows[J].Journal of Hydraulic Engineering,2004,4:341 -348.
[5]谭 平,徐 蕾,凌晓聪,动力管道水锤激振分析[J].南京理工大学学报,2006(2):182-185.
[6]景思睿,张鸣远.流体力学[M].西安:西安交通大学出版社,2001.
[7]蔡亦钢.流体传输管道动力学[M].杭州:浙江大学出版社,1989.
[8]张 慧.武器压力测试中传压管道的动态特性研究[D].南京:南京理工大学,2006.
[9]谢坡岸.蓄能器对管道流体脉动消减作用的研究[J].噪声与振动控制,2000(2):2-5.
[10]姚荣康,朱昌明,詹永麒.带皮囊式蓄能器的油压缓冲器仿真与试验[J].系统仿真学报,2005,17(11):2741 -2744.
[11]黄益民,刘 伟,刘永寿,等.充液管道模态的参数灵敏度及其共振可靠性分析[J].振动与冲击,2010,29(1):193-195.

