横向补给系统高架索在一重和双重内共振下的面内振动

张良欣，何学军，任爱娣

(海军工程大学 后勤指挥与工程系，天津 300450)

高架索在横向干货补给过程中，由于受到集中质量(货物)在高架索上的位置的变化、高架索两端高度差以及船舶运动引起的索端的激励等因素的影响，使得高架索系统的动力学行为异常复杂。目前对于横向干货补给系统的高架索研究还主要局限于静力学、结构计算及优化设计等方面［1－4］，对于作为横向补给高架索系统的控制设计基础的动力学特性的研究还很少。横向补给高架索系统的动力学模型可以近似简化为具有集中质量的倾斜悬索，其动力学特性研究可借鉴类似悬索的动力学研究成果。陈自力，唐驾时［5］针对工程客、货运索道系统，利用δ函数来体现集中载荷对悬索的影响，建立了外激励作用下、具有移动集中载荷的两端固定的水平悬索的动力学模型;通过利用Galerkin离散与多尺度方法对系统进行渐近分析，得到了系统主共振/次共振分岔点的解析解、分岔点位置以及相应分岔图，还分析了系统的分岔和稳定性。Lin和Perkins［6］建立了具有若干集中质量悬索的三自由度线性振动模型，提出了可用于求解任意垂度悬索特征解的半解析半数值的方法，拓展了以往分析悬索—质量系统动力学受限于模态阶数的理论方法。Rega等［7］对倾斜悬索的动力学特性进行深入研究，研究表明其面内振动的模态频率与水平悬索存在本质区别，倾斜悬索不存在对称和反对称模态，其模态形式为混合型(非对称)模态。模态频率与弹性—几何参数关系也不象水平悬索那样对称与反对称模态频率存在交叉点，而是各阶模态频率曲线分离。Takahashi［8］参照Irvine［9］水平悬索线性频率计算公式，考虑悬索倾斜角度的影响，推导出用于计算倾斜悬索频率的改进的Irvine公式，并与Galerkin离散结果、Irvine理论结果比较，结果表明，改进的Irvine公式具有很高的精度。本文综合上述文献的建模思想，考虑到集中质量等因素的影响，建立了高架索的面内振动理论模型。利用Galerkin方法对系统进行了离散，得到了高架索系统的前3阶模态振动的标准控制方程。借助Mathematica软件，分析了集中质量在高架索上的位置对系统各阶模态频率的影响;同时，利用数值方法对1∶1∶2双重内共振及1∶2内共振两种情况下系统的面内振动特性进行分析。

1 控制方程建立及简化

综合文献［4］－文献［9］，考虑到集中质量在高架索上的位置对系统的动力学行为的影响，高架索系统平面内振动的动力学模型为:

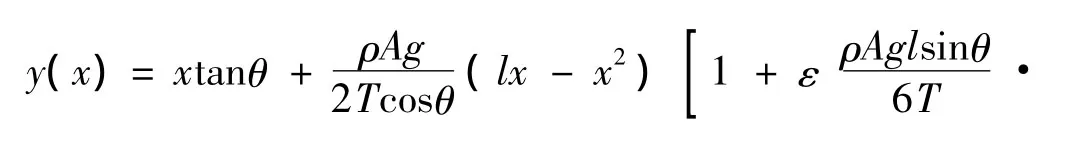
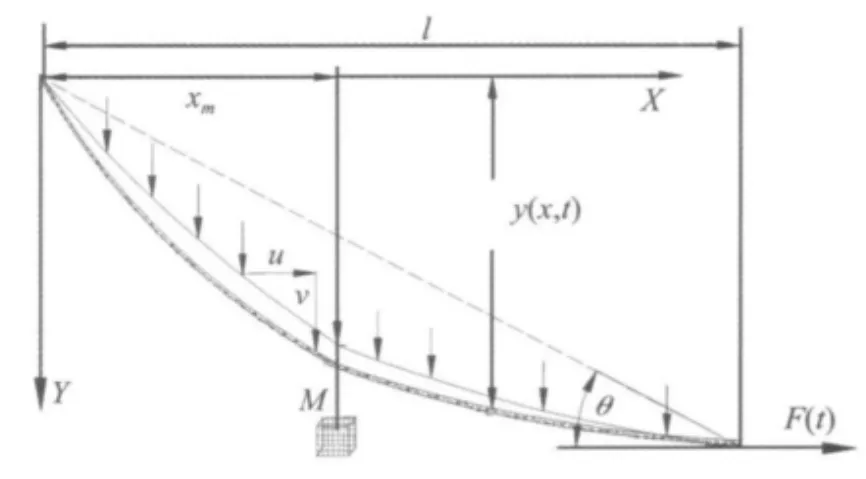
图1 高架索系统的示意图Fig.1 The schematic model of highline cable

为了研究高架索系统的面内横向振动，将高架索的轴向运动做为激励简化高架索面内控制方程。考虑参数激励情况，根据边界条件［10］u(0，t)=0，u(l，t)=lF(t)，对方程(1a)分别进行边界积分，得:

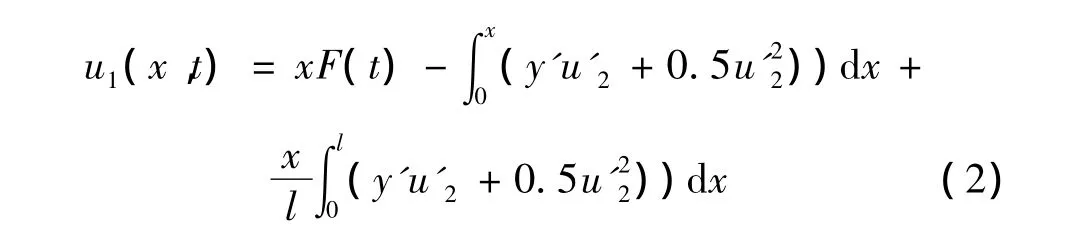
将式(2)代入式(1b)，可得高架索系统的面内横向振动的控制方程:

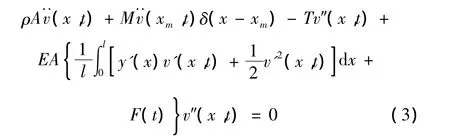
式中F(t)=f sin(Ωt)为高架索的索端无量纲参数激励，f为无量纲常数，Ω为激励频率。

其中λn为材料弹性－几何参数，考虑到集中质量及高架索倾角的影响［8］，其具体表达式为:

由式(7)可见，高架索系统的材料弹性－几何参数与集中质量的位置、模态振型因素有关，这也是高架索系统与无集中质量的悬索的重要区别之一。通过上述各表达式可见，集中质量对高架索系统的动力学行为的影响，不仅仅体现在对系统惯性质量的影响，同时还与高架索系统的频率方程、振型方程中的系数有关，进而影响系统的模态振型和模态频率，这种强耦合特性，大大增加高架索系统的动力学行为研究的难度。

2 高架索系统面内振动的模态频率分析

由上述初步分析可见，高架索系统的模态频率、振型将随集中质量的在高架索上的位置变化而变化，只有明确了系统模态频率、振型的变化趋势，才能更好地为后续的高架索系统的动力学研究的开展铺平道路，因此，必须首先确定系统模态频率与集中质量的位置的关系。

由式(5)、式(6)以及式(7)可见系统模态振动的振型及模态频率是相互关联的，表达式εn、λn中均含有集中质量在高架索上的位置xm这一基本参数。但是，即使给定xm的值，也无法确定系统振动模态振型及频率，因此称xm为局部参数。φn(xm)对应特定集中质量位置的n阶模态振型幅值，体现了集中质量对系统质量的贡献，如果先不考虑 xm的取值，直接给定φn(xm)的值，就可以确定参数εn、λn及高架索系统振动的模态振型和模态频率，因此称之为系统的全局参数。

本文通过待定局部参数 xm，而给定全局参数φn(xm)的方式来确定参数 εn、λn，进而由式(5)、式(6)得到高架索系统振动的n阶模态频率ωn及模态振型φn，再由式(5)反过来确定局部参数xm的值。通过改变φn(xm)的值，重复上述步骤，即可以得到高架索系统面内振动的n阶模态频率与集中质量位置的关系，为系统后续的动力学行为研究提供基础。其中，φn(xm)的取值范围为(0，1)。借助Mathematica程序，得到了高架索系统的前3阶模态频率与集中质量位置的关系曲线，如图2所示

图2 高架索系统的前3阶模态频率与集中质量的位置的关系及各阶模态振型(xm=5 m)Fig.2 The first three modal frequencies influenced by the lumped mass of highline cable and modal shapes when xm=5 m

由图2可见，高架索系统各阶模态频率受集中质量的位置变化的影响很大，当xm≈4 m～6.6 m时，高架索系统的第1、3阶模态频率存在类似滞回非线性的特性，即同一位置对应多个模态频率、振型。说明集中质量在特定位置时，系统将会存在几种不同的振动形式。此外，数值分析表明，当xm≈4.5 m ～5.5 m 时，系统的第1、2、3阶振动存在1∶1∶2双重内共振情况;图2给出了xm=5 m时，系统发生1∶1∶2双重内共振及1∶2内共振情况的振型图，后续的数值分析就是针对该情况进行的。本文通过选取不同的第1阶模态频率产生1∶1∶2 双重内共振及1∶2 内共振情况。系统发生1∶1∶2双重内共振时，第1阶模态振型(O1(r))、3阶模态振型(O3(u/r))呈现近似的反对称特征，第2阶模态振型(O2(u/r))为典型的混合(非对称)模态;而发生1∶2内共振时，系统的第1阶模态振型(O1(u))为近似的对称模态，第2、3阶模态振型与双重共振情况相同。

3 数值分析

参照实际情况，高架索系统的基本参数取值如下:

E=1.8 × 1011Pa;A=4.9 × 10－4m2;ρ≈7800kg/m3;l=50 m;xm=5 m;M=600kg;T=20 kN;f=0.01;θ=π/6。

Ω为高架索的索端激励频率，选取Ω=2ω1，为一类典型参激共振情况。下面就针对1∶1∶2双重内共振(ω3=2ω1≈2ω2)及 1∶2 内共振情况，对高架索系统在平面内的横向振动的动力学特性进行数值分析。

情况1 1∶2 内共振情况(ω3≈2ω1)

由上述的高架索系统的模态频率的计算，发生1∶2内共振时系统的各阶模态频率及小参数取值为:ε1=0.0461;ε2=0.0578;ε3=0.1505;ω1=5.3707 rad/s;ω2=6.3252 rad/s; ω3=12.5482 rad/s;

由图3、图4可见，对于1∶2内共振情况，高架索系统面内振动以第1阶模态振动为主的周期运动;高架索系统的第2、3阶模态振动的振幅迅速衰减，与第1、2阶模态振动相比，系统的第3阶模态振动完全可以忽略不计。

情况2 1∶1∶2 双重内共振情况(ω3=2ω1≈2ω2)

系统各阶频率及小参数取值为:

ε1=0.0818;ε2=0.0578;ε3=0.1505;ω1=6.2745 rad/s;ω2=6.3252 rad/s;ω3=12.5482 rad/s。

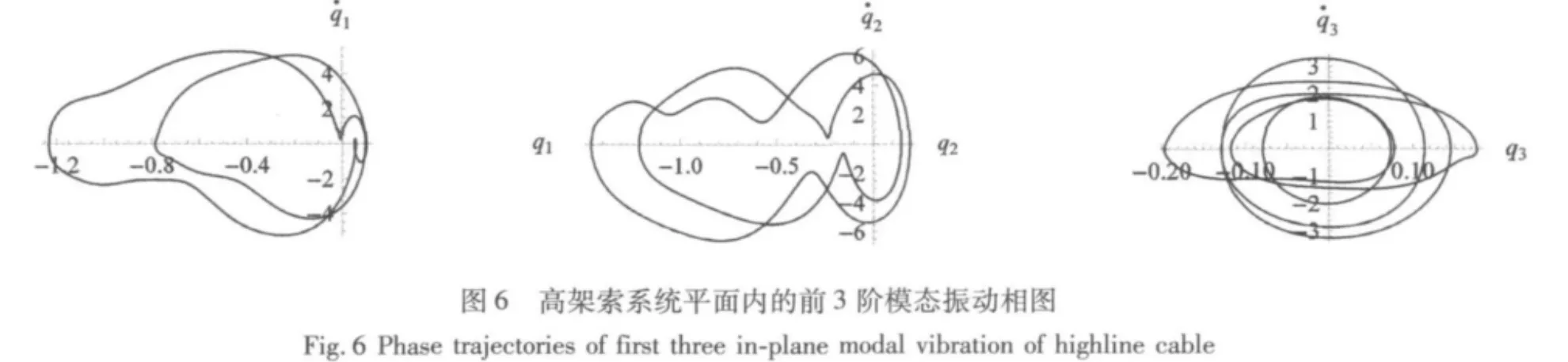
由图5、图6可见，对于1∶1∶2双重内共振情况，高架索系统的振动以前两阶模态振动为主，第2、3阶模态振动的振幅比1∶2内共振情况大得多。由于此时系统的前两阶模态振动频率十分相近，使得系统第1、2、3阶模态发生1∶1∶2双重内共振时，第2阶模态也处于近共振状态，从而导致系统的振动出现第2阶模态振幅较大的情况。同时，系统的各阶模态振动也不再是简单的周期运动，高架索系统的第1、2阶振动为周期2运动，而第3阶振动更为复杂，为周期5运动。

综上所述，当 xm≈4.5 m ～5.5 m 时，高架索系统将存在1∶1∶2双重内共振及1∶2内共振两种振动形式，系统在扰动下可能会在这两种振动之间跳跃，从而影响到系统的作业效率，甚至导致系统的稳定性。因此，对于该高架索系统而言，在该区间作业时，应尽量保持高架索系统张力及货物运行速度的恒定，避免在该区域内调节货物输送的速度。

4 结论

考虑集中质量在高架索上的位置变化对系统动力学特性的影响，建立了横向补给系统的高架索面内振动的连续体模型，利用Galerkin方法将连续模型离散为标准的动力学控制方程。引入全局和局部参数的概念，分析了集中质量的位置对系统的前3阶模态频率的影响，得到了他们的关系曲线。对1∶1∶2双重内共振和1∶2内共振情况下高架索系统的参激振动的动力学行为进行研究，结果表明，高架索系统在发生1∶1∶2双重内共振时，系统振动的第2、3阶振幅值较1∶2内共振情况大得多，且存在复杂的周期2、周期5运动现象。

［1］卢永锦.海上横向补给高架索道系统数学模型研究［J］.中国造船，1996，37(1):17－22.

［2］余建星，李红涛.高架索海上补给装置在小型船舶补给上的应用［J］.海洋技术，2005，24(2):59－62.

［3］严梅剑.海上航行横向补给装置选型设计［J］.船舶，2004，31(1):51－53.

［4］杨 军，徐岩山，任爱娣，等.海上补给仿真训练系统中高架索形态模型研究［J］.海军工程大学学报，2006，18(4):90－95.

［5］陈自力.集中荷载作用下悬索的面内运动非线性分析与应用［D］.长沙:湖南大学，2006.

［6］Lin H P，Perkins N C.Free vibration of complex cable/mass systems:theory and experiment［J］.Journal of Sound and Vibration，1995，179(1):131－149.

［7］Rega G，Srinil N.Nonlinear hybrid-mode resonant forced oscillations of sagged inclined cables at avoidances［J］.Journal of Computational and Nonlinear Dynamics，2007，2(4):324－336.

［8］Wu Q，Takahashi K，Nakamura S.Formulae for frequencies and modes of in-plane vibrations of small-sag inclined cables［J］.Journal of Sound and Vibration，2005，279(3 － 5):1155－1169.

［9］Irvine H M. Cable structures［M］.Cambridge:The Massachusetts Institute of Technology Press，1981.

［10］Nayfeh A H，Mook D T.Nonlinear oscillations［M］.New York:Wiley-Interscience，1979.

附 录