快速多极子边界元法在吸声材料声场计算中的应用

崔晓兵，季振林

(哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001)

自 Rokhlin［1］于 1983年提出快速多极子法则(FMA)以来，FMA在分子动力学、电磁学、声学、流体力学等领域得到了迅速发展［2－7］。在声学方面，将其与边界元法(BEM)相结合，形成了快速多极子边界元法(FMBEM)，鉴于其在求解声场问题中计算速度快，精度高，节约内存等优势，使其成为处理大尺度声场问题的有效工具，为边界元法的发展带来了新曙光。

目前FMBEM的应用多局限于空气介质的单区域声场计算，其在多区域多介质复合声场问题中的应用成为声学FMBEM发展的新方向，将子结构技术应用于FMBEM中，发展形成子结构FMBEM［8］，能有效地解决多区域复合声场问题，使带有薄壁结构的声场计算(如内插管消声器，穿孔管消声器等)成为可能。然而，对于FMBEM在吸声材料介质或多介质复合的声场中的应用，由于复数形式波数的影响，其多极子展开式的适用性及求解精度还有待考察，复波数条件下展开式数值计算的参数选取仍需进一步研究与分析。

鉴于此，本文对复波数及实波数下的格林函数及其法向导数多极子展开式进行数值研究，建立四点单级和多极传递关系模型，通过与理论值比较，考察其计算精度，分析其误差的影响因素及来源，并找到解决此问题的方法。最后以膨胀腔阻性消声器传递损失计算为例，比较FMBEM与BEM的求解精度，验证本文方法的有效性与可行性。

1 复波数条件下的多极子展开式

1.1 边界积分方程

图1为边界平滑的三维内部声场示意图，包含刚性边界、振动边界、吸收边界三种边界。假设稳态声场声压随时间变化是简谐的，取时间项为exp(－ jωt)，其中 j=，则该声场满足三维Helmholtz方程，边界上P点处声压可由Kirchhoff-Helmholtz边界积分方程［9］得到:

图1 平滑边界内部声场示意图Fig.1 Illustration of an interior sound field with smooth boundary

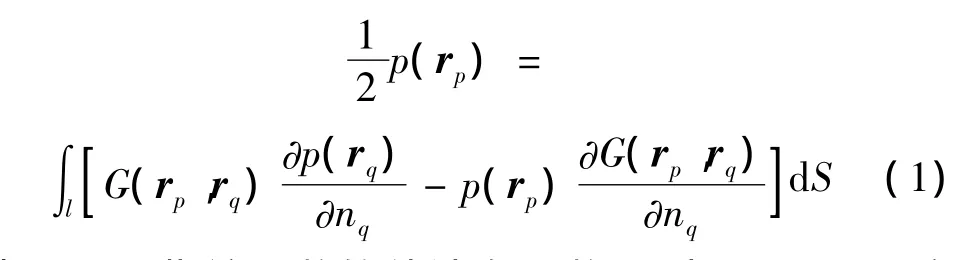
其中，∂/∂n指该函数的外法向导数，G为Helmholtz方程的基本解，形式如下:

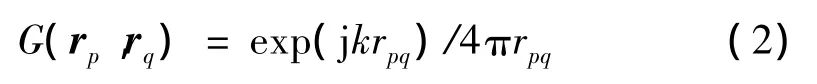
众所周知，式(1)即为传统BEM的核心控制方程，将该控制方程离散，通过某特定方法(1/8子组划分法，1/2子组划分法等)对边界节点进行分组，分级，按照每级中各组集的远近关系将声场分为近场与远场，在近场仍用传统BEM法求解，远场则采用快速多极子方法加速求解［2］，最后将两部分结果相加即可得到整个声场的系数矩阵和向量积。此种求解声场问题的方法即为FMBEM(具体实现过程可参考文献［10］)。

1.2 Helmholtz方程基本解的多极子展开式

为了在远场应用 FMA求解，需将边界积分方程等效为多极子展开式进行计算，而Helmholtz方程基本解即格林函数的多极子展开是FMBEM顺利实施的前提，其展开式的计算精度尤其成为FMBEM成功的关键。

如图2所示四点关系，M为多极子展开点，L为本地展开点。根据Gegenbauer附加定理［11］及平面波展开公式［12］，格林函数可展开成:

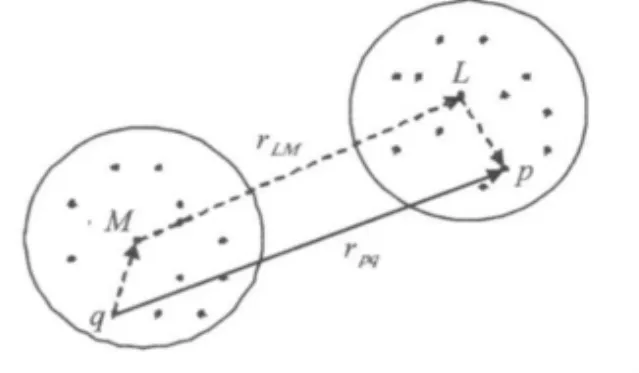
图2 四点关系图Fig.2 Geometry of the four points

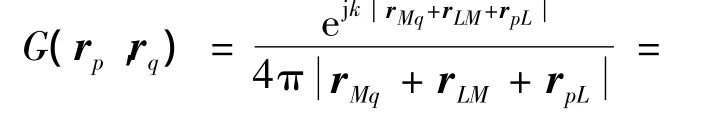
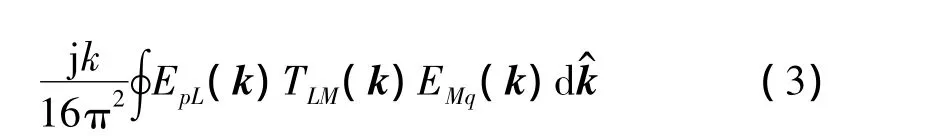
其中:

为保证式(3)成立，要求 rpL＜rLM且 rMQ＜rPM。，为波数矢量是单位球面积分向量为第一类球汉克函数，pl为勒让德多项式。声传播介质为空气时，k=2πf/c0为实波数，当传播介质为吸声材料时，假设吸声材料介质分布均匀，且声波以简谐波的形式传播，则在该介质中，密度与声速均可等效为复数形式的声参数，从而波数k=kr+j ki为复波数，代入式(3)可得:

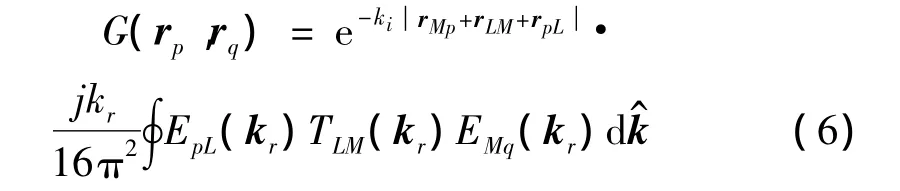
格林函数外法向导数为:

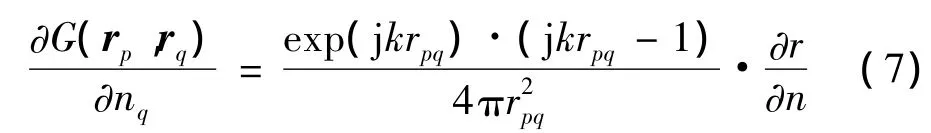
由于:

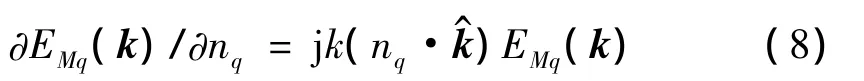
其外法向导数可展开为:

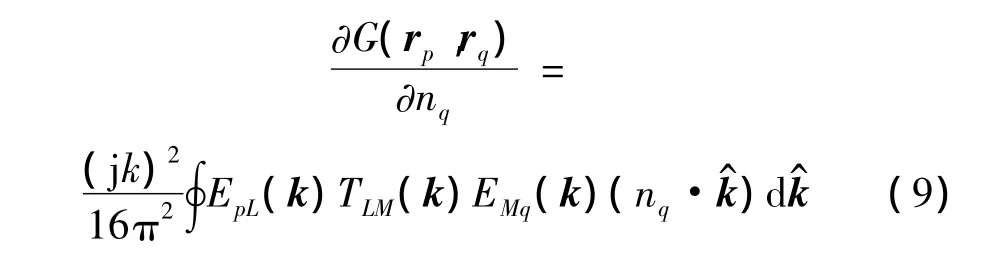
在进行远场多级影响系数计算时，根据快速多极子算法，格林函数需由下式计算:

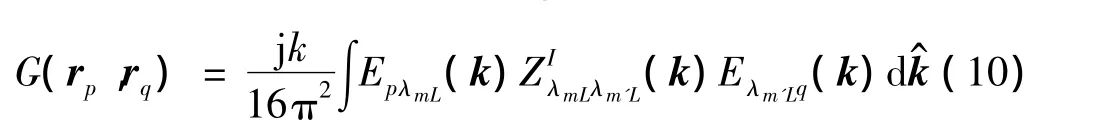
式中:

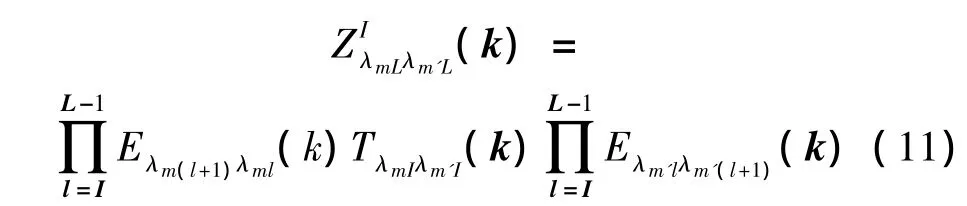
其中，L为最低级级数(级数最高)，λmL为L级m组的中心点;λm'L为L级m组的某交互组的中心点(关于近场组、交互组等概念参见文献［10］);级数I由p点、q点位置关系决定。由于2级之后才有交互组出现，因而上述两式适用于L≥3的情况。同理格林函数法向导数的多极表达式为:

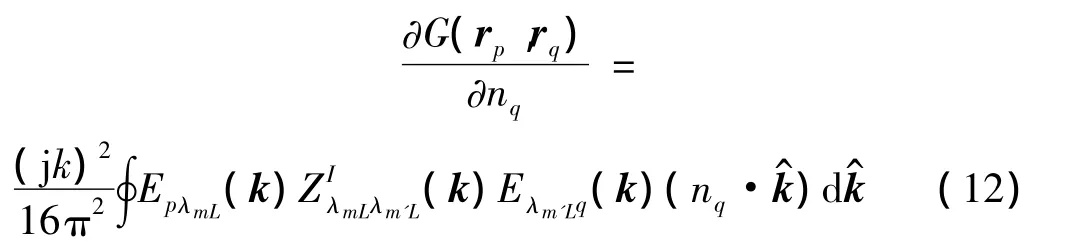
1.3 多极子展开式的数值计算

为了进行有效的数值计算，式(5)需用前Nc项和近似，考虑到复波数的影响，为使展开式在各种情况下得到足够的精度，Nc可由下式计算:

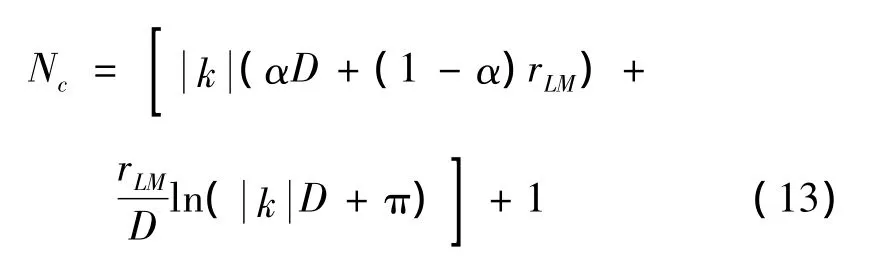
可见，Nc及Nθ的取值直接影响着多极子展开式的求解精度。在空气介质条件下，即实波数条件下，Yasuda和Sakuma［14］对 Nc及 Nθ等参数的选取做了详细的数值研究与论证，并提出了恰当的经验公式以保证展开式的计算误差在允许的范围。然而，当声波在吸声材料介质中传播时，复波数的介入对展开式计算精度的影响，以及经验公式在复波数环境下的适用性等许多问题仍需进一步研究与讨论。

2 复波数下多极子展开式的数值研究

在复波数条件下，考虑到格林函数值若按式(6)计算，衰减项ki的介入会使其随着多极子点间距离与ki的增大而迅速衰减，而若按式(3)计算，多项式的求和可能会使其衰减效应大大减小，从而产生误差。鉴于此，为了考察复波数对格林函数及其法向导数展开式计算精度的影响，取L点、M点、p点、q点各自之间距离最远的情况，针对图3所示单级和多极传递关系，数值计算各展开式值并与理论值比较，分析讨论其计算误差及产生原因。

以1/8子组划分法为例，如图3所示四点三维关系图，(a)图为单级传递关系图，由于其最低级为2级，其格林函数及其法向导数的展开式值可直接由(3)式和(9)式计算。(b)图为多级传递关系图，由p、q点位置关系可知级数I为2，其最低级为4级，因而其格林函数及其导数的展开式值由式(10)和式(12)计算。图中 q1即 λm4，q2即 λm3，M 即 λm2，L 即 λm2'，p2即 λm3'，p1即λm4'。吸声材料为长纤维玻璃丝绵，实验测得该吸声材料的特性阻抗Zb和波数kb的表达式为:

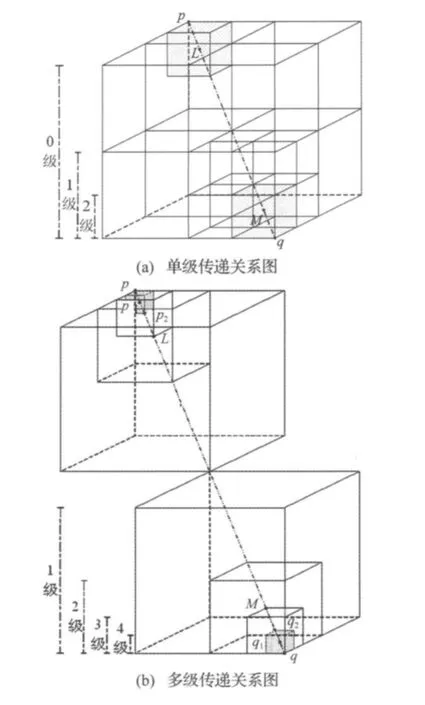
图3 四点三维关系图Fig.3 Geometry of the four points in three dimensions

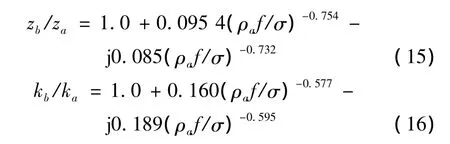
其中:za和ka分别为空气的特性阻抗与波数，ρa为空气密度，当材料的填充密度为200 g/L时，测得此材料的流阻率σ为17378 Rayls/m。吸声材料流阻率的测量方法可参考文献［15］。

2.1 单级传递

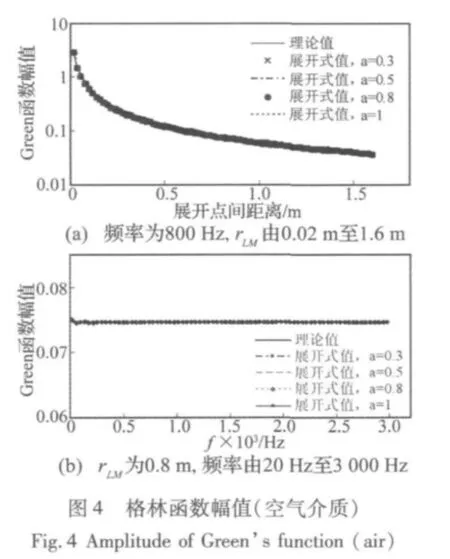
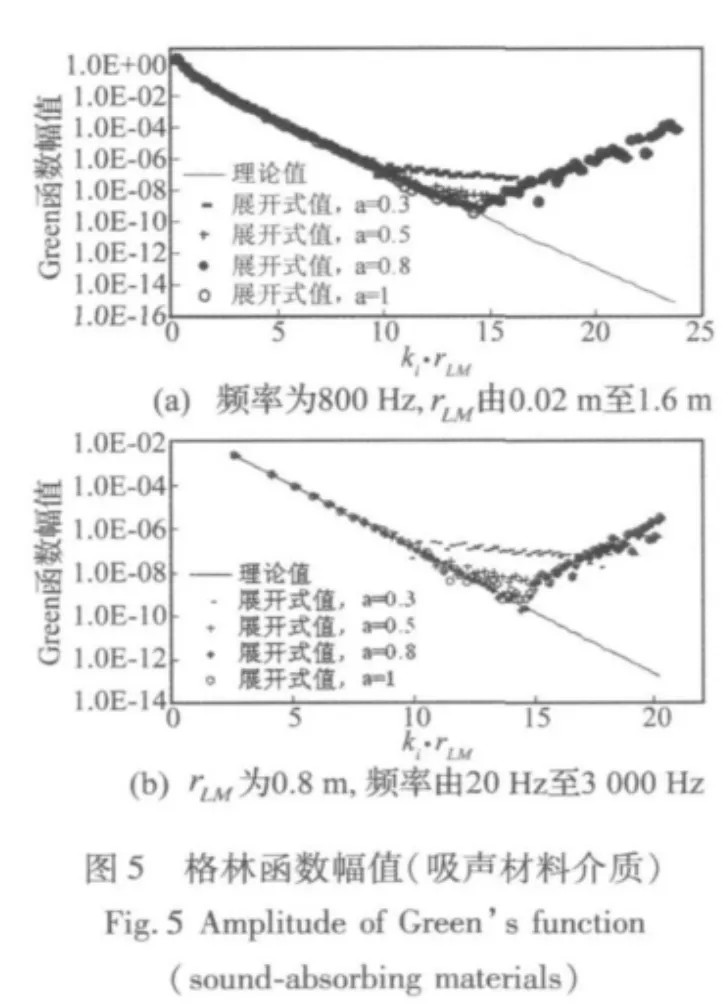
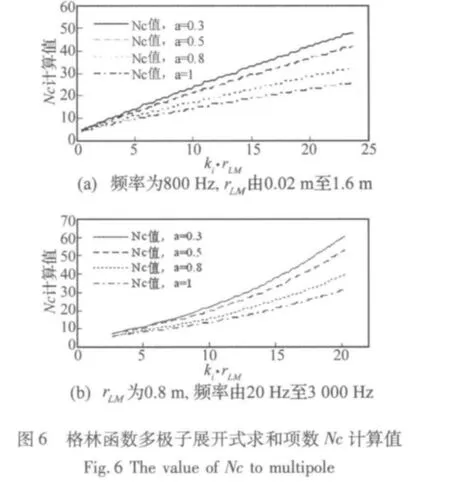
以图3(a)所示四点单级传递关系为例，计算式(2)格林函数理论值与式(3)展开式值，得到图4至图6。观察图4和图5发现，在空气介质中，无论式(13)中α取何值(0～1)，格林函数展开式值均能保证较高的计算精度，而对于吸声材料介质，当ki·rLM达到某值后，其展开式值会随着ki·rLM的增大而与理论值愈发背离。图5展示了当α取不同值时，展开式值与理论值的吻合情况，可见在两种变化方案中(定频率，变rLM;定rLM，变频率)，α取0.8时吻合情况最好，失真范围最小。而且，无论是改变rLM还是改变频率，展开式值与理论值的分歧点均与ki·rLM值密切相关，约为13。图6为在两种变化方案中，α取不同值时Nc随ki·rLM值的变化曲线，结合图5可知，在ki·rLM小于13时，只有α=0.8的Nc值对复波数展开式求解最为合适，过大或过小均会对其计算精度产生影响。

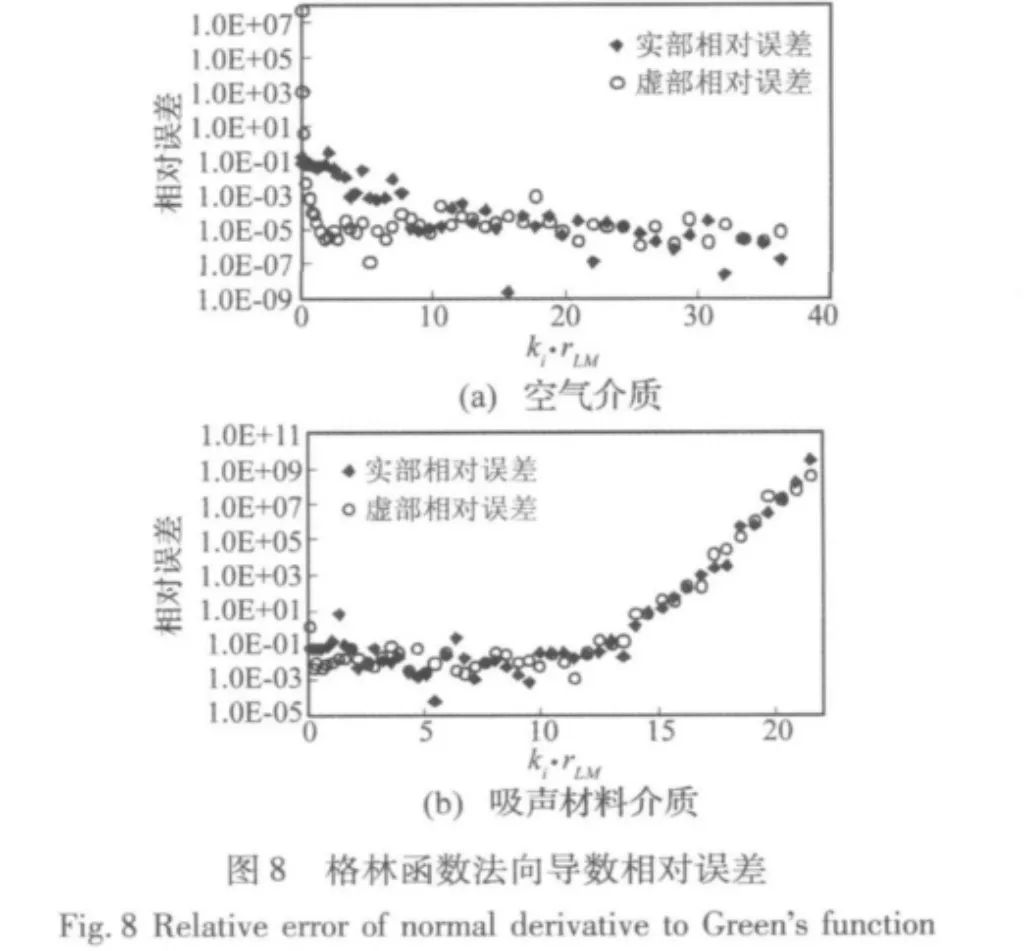
取式(13)中α=0.8，同时变化频率与rLM值，计算式(9)格林函数法向导数展开式，并与式(7)所示理论值比较，得到图7和图8。观察图7可见，在空气介质中，法向导数展开式值与理论值基本吻合，具有较高的计算精度，而对于吸声材料介质，则在ki·rLM约大于13后，开始与理论值相背离。图8展示了两种介质下计算值实部和虚部的相对误差，可见对于实波数，除了在k·rLM很小时相对误差较大外，在其他范围均有较高的精度。而对于复波数，只有在ki·rLM小于13时的误差基本在允许范围。

2.2 多级传递

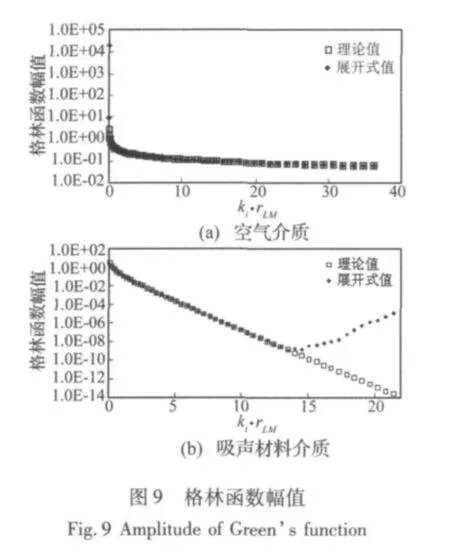
以图3(b)所示四点多级传递关系为例，取式(13)中α=0.8，同时变化频率与rLM值，计算式(2)格林函数理论值与式(10)远场展开式值，得到图9和图10。观察两图发现，多级传递关系并未增加展开式在复波数条件下的失真范围，均在ki·rLM约大于13时与理论值发生背离，其与单级传递具有相似的误差精度。由此可断定，式(3)中E(k)项的计算在实波数和复波数条件下均能保证较高的计算精度，误差主要集中在TLM(k)项的计算中，分析其误差原因为:由于TLM(k)叠加项中h(1)l(krLM)的幅值随着l的增大而逐渐增大，且其相位交替变化，由于Nc值随着ki·rLM的增大而不断增高，过大的求和次数使函数幅值得以积累，导致最终解向极大值发散。

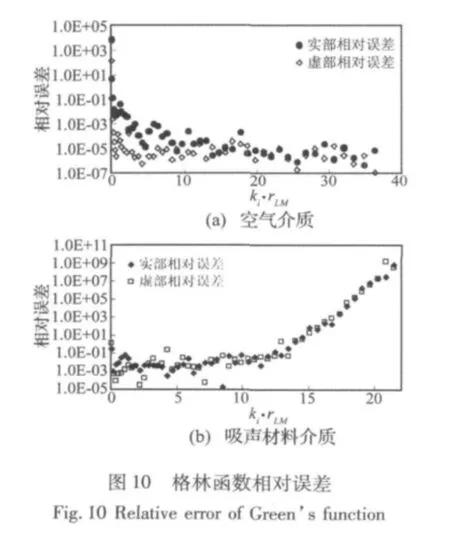
总之，实波数条件下，格林函数及其法向导数展开式的计算只在频率或rLM值极低时有较大误差，其余范围具有较高的计算精度，而且其对求和项数Nc的选取适应性强。复波数条件下，当ki·rLM超过某值时，展开式计算误差会越来越大，展开式的计算精度对Nc值的选取比较敏感，过大或过小均对求解精度及可信值范围有较大影响。

所以，对于FMBEM在吸声材料中的应用，可选取α =0.8时的Nc值，当ki·rLM大于13时，不可再用原展开式计算，鉴于此时格林函数及其法向导数值为10－9或10－8的数量级，且会随着ki·rLM的增大而越来越小，为了实现FMBEM的编程计算及满足工程应用的精度要求，可将展开式中TLM(k)的值近似为0。除此方法外，应用子结构FMBEM，将大尺寸结构模型划分为若干小尺寸结构分别计算，即可有效的避免产生过大的ki·rLM值，保证展开式有较高的计算精度。

3 计算实例

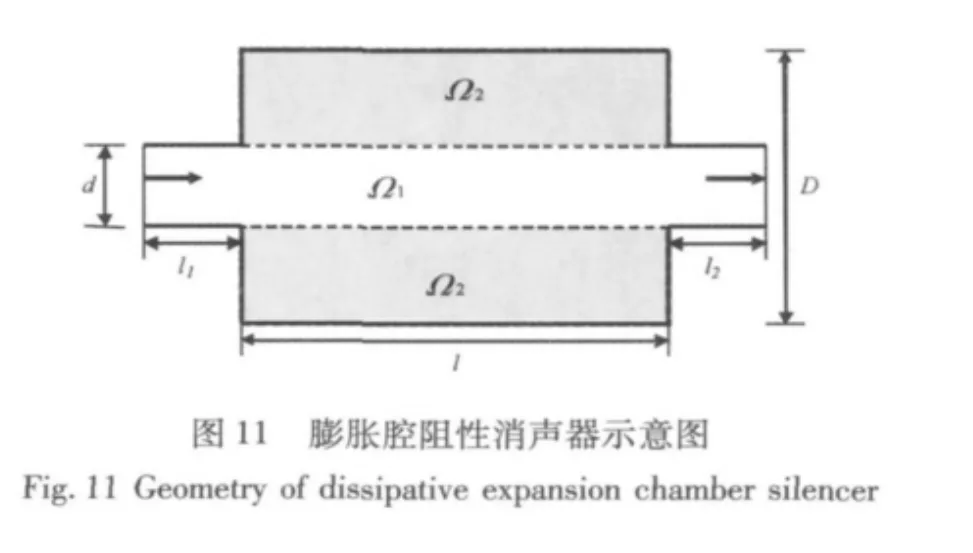
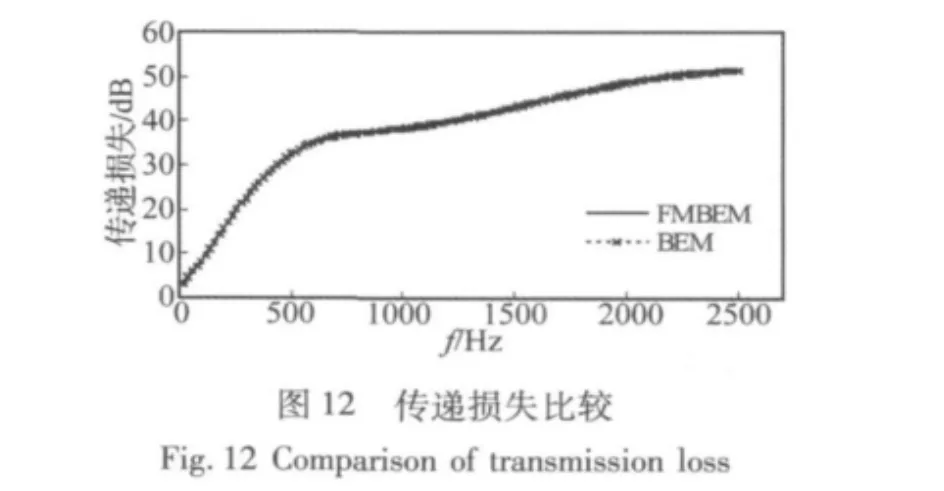
图11所示为某膨胀腔阻性消声器示意图，其尺寸为 d=0.1 m，D=0.3 m，l=0.47 m，l1=l2=0.1 m，空气中声速c=344 m/s，吸声材料为长纤维玻璃丝绵，材料填充密度为200 g/L，穿孔管只考虑其支撑吸声材料的作用。若应用FMBEM计算，则其根组边长b至少为0.67 m，在2级交互组中，约为 0.87 m，可知当ki约大于15时，即频率大于820 Hz时，展开式的计算将进入错误值范围，选用上节中提到的办法，取α=0.8时的 Nc值，当 ki·rLM大于13时，将展开式中TLM(k)的值近似为0。为了实现FMBEM在多介质复合声场中的计算，应用子结构FMBEM将此模型按传播介质分为如图Ω1与Ω2两子结构，计算其传递损失，并与子结构BEM［16］比较其求解精度。图12展示了应用子结构FMBEM与BEM计算其传递损失曲线，可见，当频率大于820Hz时，二者计算结果仍吻合良好，证实了该方法的有效性与可行性。

4 结论

本文通过对格林函数及其外法向导数展开式的数值计算与研究，发现吸声材料介质对FMBEM展开式的计算精度有重要影响，由四点单级传递和多极传递关系的计算，揭示了误差的大小与复波数的虚部值和展开点间距离的乘积有重要关系。通过与空气介质中展开式的计算比较发现，复波数环境下展开式的计算对Nc值的选取十分敏感，取式(13)中α=0.8时的Nc值能保证较大范围的求解精度，但当ki·rLM大于13时，展开式值开始与理论值相背离。

鉴于此，对于FMBEM在吸声材料声场中的应用，本文提出了两种解决办法:(1)当ki·rLM大于13时，将展开式中TLM(k)项的贡献视为0。(2)利用子结构FMBEM，将大尺寸结构划分为若干小结构分别计算，即可有效的避免产生过大的ki·rLM值，保证展开式有较高的计算精度。最后，通过对某膨胀腔阻性消声器的传递损失计算，证实了本文所述方法与技术的有效性与可行性。

［1］Rokhlin V.Rapid solution of integral equations of classical potential theory［J］.Journal of Computional Physics，1983，60:187－207.

［2］Nishimura N.Fast multipole accelerated boundary integral equation methods［J］.American Society of Mechanical Engineers，2002，55(4):299 －324.

［3］王雪仁，季振林.快速多极子声学边界元法及其应用研究［J］.哈尔滨工程大学学报，2007，28(7):752－757.

［4］Zhao J S，Chew W C.Three-dimensional multilevel fast multipole algorithm from static to electrodynamics［J］.Microwave Opt.Technol.Lett.，2000，26:43 －48.

［5］Liu Y J，Nishimur N，Otani Y，et al.A fast boundary element method for the analysis of fiber-reinforced composites based on a rigid-inclusion model［J］.ASME Journal of Applied Mechanics，2005，72(1):115－128.

［6］Liu Y J.A new fast multipole boundary element method for solving 2-D stokes flow problems based on a dual BIE formulation［J］. Engineering Analysis with Boundary Elements，2008，32(2):139 －151.

［7］Fukui T，Kozuka M.Analysis of sound reflection and diffraction in half space by fast multipole boundary element method［R］.Proc of 17th Japan Natl Symp on Boundary Element Methods，2000.

［8］Yasuda Y，Sakamoto S，Sakuma T.Application of the fast multipole boundary element method to sound field analysis using a domain decomposition approach［C］.Proceedings of INTER-NOISE 2006(Honolulu)，2006:624.

［9］Pierce A D.Acoustics:an introduction to its physical principles and applications［M］. McGraw-Hill:New York，1981.

［10］Sakuma T，Yasuda Y.Fast multipole boundary element method for large-scale steady-state sound field analysis.part I:setup and validation［J］.Acta Acustica United with Acustica，2002，88:513－525.

［11］Abramowitz M，Stegun I A.Handbook of mathematical functions［M］.Dover:New York，1965.

［12］Rokhlin V.Diagonal forms of translation operators for the Helmholtz equation in three dimensions［J］.Applied and Computational Harmonic Analysis，1993，1(1):82 －93.

［13］Koc S，Chew W C.Calculation of acoustical scattering from a cluster of scatterers［J］.The Journal of Acoustical Society of America，1998，103:721 －734.

［14］Yasuda Y，Sakuma T.Fast multipole boundary element method for large-scale steady-state sound field analysis.Part II:examination of numerical items［J］.Acta Acustica United with Acustica，2003，89:28－38.

［15］Standard test method for airflow resistance of acoustical materials［R］.American Society for Testing and Materials ASTM C 522－87，1993，Philadelphia PA.

［16］季振林.穿孔管阻性消声器消声性能计算及分析［J］.振动工程学报，2005，18(4):453－457.