船用柴油发电机组非线性隔振系统动态特性分析
高浩鹏,黄映云
(海军工程大学 船舶与动力学院,武汉 430033)
柴油发电机组作为舰船电站系统的原动力仍在广泛运用,为舰船的武器系统、导航系统、指挥系统等提供动力源,所以其经常性的使用是必不可少的。柴油机其本身作为一种机械系统,在将化学能转化为机械能时,其动力传递组件的复杂机械运动使得发电机组本身成为船体的一个重要激励源[1]。考虑到舰船的隐身性,对柴油发电机组安装隔振系统亦被广泛使用。目前对非线性隔振系统特性分析大都通过数学模型进行求解[2],而这种方法主要分析隔振系统自身的特性并且应用于工程实际较为繁琐,对产生激励的机械与隔振系统综合起来分析较少。本文对TBD234V6柴油机发电机组及其线性隔振系统进行多体动力学建模,并通过实验验证了模型的正确性;在此基础上建立了发电机组非线性隔振系统,综合考虑到激励源与隔振系统的相互影响,对系统的动态特性进行分析研究。
1 线性隔振系统的建模与实验验证
1.1 多体动力学模型的建立
本文对柴油发电机组进行三维实体建模,并通过CAE技术建立机组的多体动力学模型;该模型的多体动力学边界条件较为复杂[3],主要包括柴油机发火顺序及间隔角、气缸压力、各个刚体之间的约束(如图1所示)、刚体之间的力元等。模型利用柴油机调速器原理合理实现了柴油机启动工况和稳定工况的模拟,为隔振系统的动态特性分析奠定了基础。

图1 组件间的约束关系Fig.1 The constrain relation of subassembly
在多体动力学模型建立的基础上,本文通过衬套力来建立线性隔振系统;为了以便通过实验验证模型的正确性,文中隔振器的参数选取与实物EA400隔振器的参数一致,动刚度横向、纵向、垂向[4]分别为1700 N/mm、5000 N/mm、6500 N/mm,阻尼比取 ζ=0.1。柴油发电机组整机的多体动力学及线性隔振系统模型如图2所示(为了便于观察,图中隐藏了机体以及一些外挂件等)。

图2 机组及隔振系统实体模型Fig.2 The model of diesel and vibration isolation system
1.2 实验验证
柴油发电机组的建模过程相当复杂,然而模型的正确性直接影响计算结果的正确性,所以应对模型的正确性进行实验验证。机组零部件众多,多体系统复杂,运动方式多样,对单个零件的某个参数来验证,其可测性与可验证性是很难保证的。本文选取了柴油机发电机组的振动烈度作为实验验证的参数,主要原因有:多体系统模型的建立相对于实际柴油机来讲边界条件简化了很多,对于高频信号就较难评价,而振动烈度以速度信号作为参数能较好的反应机组的中低频段特性,所以模型中易于反映出来;另外振动烈度易于测量并且反映隔振系统的性质。
GJB中评估振动烈度用的是振动速度,而实际的采样信号为加速度,所以需要采用数值积分方法得到速度信号。文中实验用的测量仪为杭州亿恒科技有限公司生产,型号是AvantLite;加速度传感器为扬州科动电子有限责任公司生产,型号是KD1005LS的ICP式三向加速度计。作者对多个测点的加速度测量并与计算结果进行对比分析(其中测点1位于柴油机B侧自由端机脚附近,测点2在B侧输出端机脚螺栓上,测点3在B1缸缸盖输出端侧面,测点4在A侧自由端机脚附近的机体上,各测点测得的振动速度有效值如表1所示),发现:多体动力学计算得到三个方向振动速度幅值由大到小依次是横向、垂向、纵向,这与实验结果一致;多体动力学计算结果的频谱图中对振动速度贡献量最大的频率是37.5Hz,这与实验结果一致;多体动力学计算结果中对结果贡献量较大的频率还有25Hz,而实验结果中这个频率对振动速度贡献量较小。对于出现25Hz,作者通过去掉气缸压力而利用运动驱动等方法发现,柴油机动力传递组件在运动时为变惯量系统,导致模型的动平衡性不是很好,所以多体动力学计算结果中25Hz对振动速度的影响较大。作者列出了额定工况下测点1实测以及对应位置计算得到的垂向速度频谱图,如图3和图4所示。
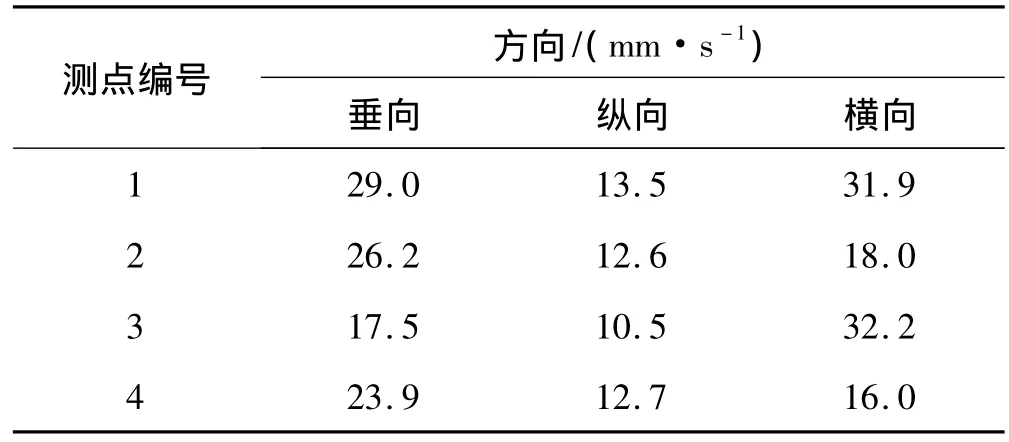
表1 实验得振动速度值Tab.1 The result of actual measurement vibration velocity


1.3 线性隔振系统特性分析
从隔振器性能的评价角度考虑,传递率是其中一个重要评价指标,其主要与系统的自然频率和激励频率有关[5]。对于柴油发电机组来讲,其正常工作时转速为1500 r/min,故其激励力的频率主要与动力传递组件的一次惯性力与气缸爆压有关,即激励频率基本为固定值,文中主要对隔振系统的自然频率进行重点分析。
本文计算的理论基础是计算多体系统动力学[6],分析得柴油发电机组对外共有7个自由度(包括机组的6个自由度和动力传递组件的1个旋转自由度)。文中利用多体动力学分析软件的振动模块对机组隔振系统性能进行分析;通过扫频的方式得到系统的固有频率和振型(如表2所示);另外分析得到动力传递组件扭转自由度的固有频率为15.1 Hz。由系统的固有频率、振型、机组的工作基频(25Hz)以及激励频率(37.5Hz)发现,系统绕垂向转动、垂向平动和绕横向转动的频率都处于非隔振区间,故判断该隔振器的选型是不合理的。

表2 线性隔振系统的固有频率和振型Tab.2 Natural frequency and mode shape of linear vibration isolation system
2 非线性隔振系统的建模
通过对线性隔振系统特性分析发现,EA400隔振器对该柴油发电机组的隔振效果不是很好,考虑到气动隔振器固有频率低、可靠性高、稳定性好等[7]特点,文中以空气弹簧为实物,根据气动隔振器的结构特性,利用三个一维弹簧来模拟空气弹簧,从而建立非线性隔振系统。文中隔振器的刚度以实验结果为基础,通过数据拟合的方式得到刚度与隔振器变形的关系曲线,如图5和图6所示;由图5中可以看出,隔振器压缩稍大于10 mm的变形开始具有明显的非线性[8],这主要是因为气囊的连接板同囊内的橡胶金属接触的这种结构所决定,这种结构在冲击载荷作用下压缩时具有很强的抵抗变形的能力。
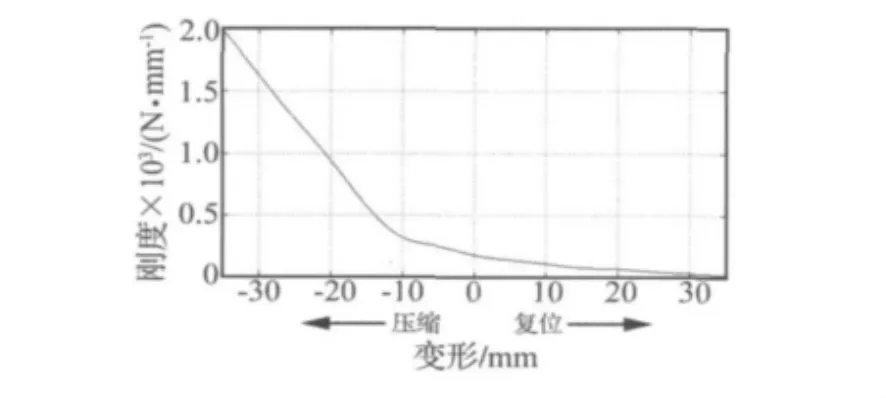
图5 隔振器垂向动刚度-变形曲线Fig.5 The vertical dynamic stiffness-deformation curve of the vibration isolators

图6 隔振器纵向动刚度-变形曲线Fig.6 The longitudinal dynamic stiffness-deformation curve of the vibration isolators
由于气囊隔振器的横向刚度特别小,故本文在建模时隔振器以30°角倾斜安装[9],使得隔振器在柴油发电机组的横向上也具有较大刚度。在多体动力学软件分析时,非线性隔振器的模拟是以力与变形的关系来添加的,其力与变形的历程曲线是通过对实验得到的刚度与变形的拟合曲线进行数值积分得到。
3 非线性隔振系统的动态特性分析
在非线性隔振系统模型建立的基础上,作者通过振动模块对系统的固有频率及振型进行分析,具体结果见表3;由表中可以发现空气弹簧的固有频率较低,远离柴油机工作的激励频率。

表3 非线性隔振系统的固有频率和振型Tab.3 Natural frequency and mode shape of non-linear vibration isolation system
3.1 与线性隔振系统的对比分析
柴油机在启动过程中由于转速的变化使得自身激励的频率逐渐递增,在启动过程中隔振器的变形量较大。柴油发电机组在静态时,线性隔振器和非线性隔振器的垂向变形分别是1.87 mm和10.23 mm;由于非线性隔振器的刚度值较线性小,故其静态变形量较大。文中在对非线性隔振器选型时主要使得隔振器动态工作在非线性区域,当柴油机工作在额定工况时(1500 r/min,186 kW),分别对线性和非线性隔振器的动态变形量(即隔振器变形最大值和最小值之差)进行分析,其数据如表4所示;虽然非线性隔振器的刚度值较线性隔振器小,但由表4可以发现非线性隔振器的横向和纵向动态变形都小于线性隔振器,说明非线性隔振器的振动传递率小于线性隔振器;图7和图8为机组额定工况时线性和非线性隔振器垂向变形的时间历程曲线。作者在对隔振器纵向变形分析时发现,由于机组的重心不在几何型心处,柴油机工作时在纵向会产生耦合振动。

表4 隔振器动态变形Tab.4 The dynamic deformation of vibration is olation


柴油机自身作为振源,对其隔振属于主动隔振问题;评价主动隔振系统的好坏就是看振源传递给基础力的大小,故本文对线性和非线性隔振系统下柴油机传递给船体的力的历程曲线进行分析,发现柴油机额定工况时传递给船体的垂向力的幅值在线性隔振系统和非线性隔振系统下分别为1694 N和282 N。为了进一步分析力的特性,作者对其进行傅里叶变换,线性和非线性隔振系统传递给船体垂向力的幅频特性如图9和图10所示。由图9和图10对比发现,非线性系统对25 Hz和37.5 Hz的激励力有很好的隔振作用。另外由图10中可以发现,在气缸压力激励频率的1/3、2、3、4次谐频处都有较明显的波峰,说明柴油机激励响应中包括高次谐波、次谐波;图10中3次谐波的幅值大于2、4次谐波的幅值,即激励响应的振幅会出现跳跃现象;这两点特性也是非线性系统区别与线性系统的特点,从反面也论证了非线性隔振系统建模的正确性。


3.2 冲击条件下非线性隔振系统动态特性分析
当船舶在冲击条件下为防止船体的振动传至柴油发电机组的问题属于被动隔振问题,由于主动隔振与被动隔振的传递率在表达式上完全相同,故文中建立的非线性系统较线性系统有良好的被动隔振效果。下面主要建立船舶虚拟冲击平台,并分析柴油发电机组工作在额定工况时冲击条件下的特性。
文中冲击条件主要模拟船体在受到水下爆炸时的冲击,根据联邦德国1985年颁布的BV043/85标准,对船体施加双重半正弦的沿柴油机横向加速度冲击,文中使用的函数为三重IF函数;其中施加冲击的开始时间是1.6 s;对基础施加的加速度时域曲线如图11所示,图中的毛刺是由于软件分析的精度以及IF函数本身易导致跳变。

图11 虚拟冲击加速度曲线Fig.11 The emulational impact curve of acceleration

图12 冲击条件下非线性隔振器横向动态变形曲线Fig.12 The transverse dynamic deformation curve of non-linear vibration isolators under impact loads
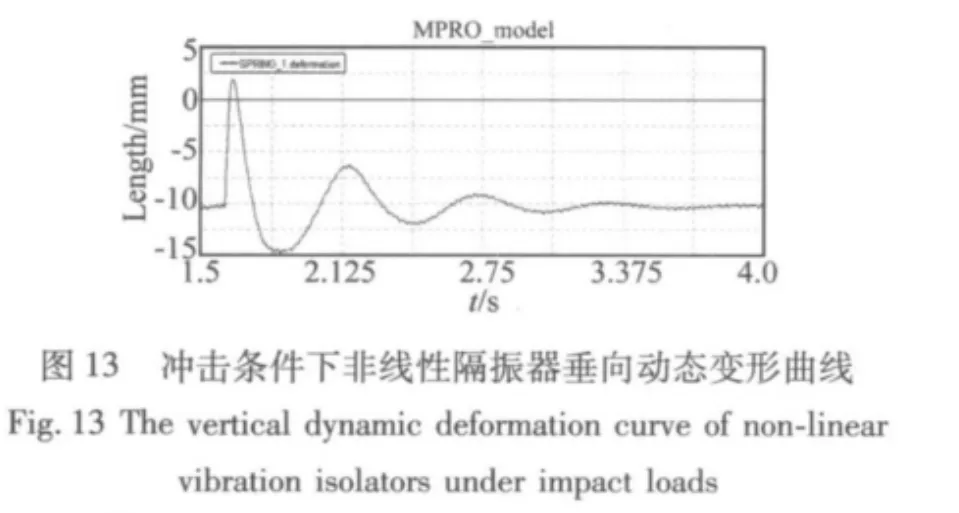
图12是柴油发电机组额定工况时隔振器横向变形曲线,由图中发现在冲击峰值时刻隔振器变形瞬间产生大的跳跃,在恢复稳定状态时又遇到柴油机动不平衡的一次惯性力,可见在冲击条件下隔振器横向变形较大,特别是机组上端的一些与船体有连接的外挂件(如烟囱),故在空间位置允许的情况下应在柴油发电机组的上端部位安装限制横向位移的气动减振器。图13是耦合作用下隔振器垂向变形曲线,由于阻尼设置较小其衰减时间较长,在衰减过程中由于隔振器非线性因素其峰峰值对应的时间差不相等。图14是柴油发电机组公共底座的横向加速度时间历程曲线,其幅值约是双重半正弦波幅值的1/10,表明气动隔振器有良好的隔振效果。

4 结论
本文主要建立了柴油发电机组多体动力学以及线性隔振系统模型,并通过实验验证了模型的正确性;在此基础上构建了非线性隔振系统模型,分析了非线性隔振系统在柴油机正常工作时的动态特性,并与线性隔振系统特性进行对比;另外构建了船舶冲击条件下的虚拟模型,并对冲击条件下非线性隔振系统的动态特性进行分析;结果表明非线性隔振系统较线性隔振系统有良好的隔振效果,特别是当船舶受到瞬时高强度脉冲激励时强非线性隔振系统的被动隔振效果较好。
柴油发电机组是船舶噪声的一个主要激励源,要对其隔振系统特性分析就首先对机组进行正确的建模,文中运用计算多体动力学方法对整个柴油机的运动机构进行系统建模,在论证模型正确性的基础上以气动减振器为实物建立非线性隔振系统并对其进行动态分析,分析结果较为可靠。文中的建模以及分析过程可应用于船舶其它机械设备,工程上可以简单实现船舶隔振系统的选型和参数优化。另外文中建立的船舶冲击条件下的虚拟模型为船舶各种机械设备甚至电子设备的抗冲击研究提供了一定的基础。多体动力学中非线性隔振系统可以简单的实现参数化设计与控制,与MATLAB等数值计算软件相结合,若能在工程运用上实现混沌控制,就可以更好的改善隔振系统的性能,具有重要的应用价值。
[1]朱孟华.船舶内燃机动力学[M].北京:国防工业出版社,1979.
[2]黄映云,吴善跃,朱石坚.囊式空气弹簧隔振器的特性计算研究[J].振动工程学报,2004,17(2):249 -252.
[3]高浩鹏,黄映云,王雪山.船用柴油机运动机构动力学动态分析方法研究[J].振动与冲击,2009,28(8):84 -87,200.
[4]何 琳,束立红,王 强.舰船用隔振器系列型谱[M].北京:中国人民解放军海军装备部,2005.
[5]师汉民.机械振动系统分析·测试·建模·对策[M].武汉:华中科技大学出版社,2004.
[6]张国庆,黄伯超,浦狄强,等.汽车发动机曲轴系动态仿真[J].系统仿真学报,2006(8):2293 -2295.
[7]Ravindra B,Mallik A K.Performance of non-linear vibration isolators under harmonic excitation[J].Journal of Sound and Vibration,1994,170(3):325 -337.
[8]朱石坚,何 琳.船舶减振降噪技术与工程设计[M].北京:科学出版社,2002.
[9]陈志敏,黄映云,彭 敏,等.基于ADAMS的船舶隔振系统性能研究[J].振动与冲击,2007,26(8):101 -103.

