小波包变换和隐马尔可夫模型在轴承性能退化评估中的应用

肖文斌，陈 进，周 宇，王志阳，赵发刚

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240;2.上海卫星工程研究所，上海 200240)

轴承是旋转机械中的关键部件，其故障是造成旋转机械故障的重要原因之一。因此，轴承一直都是设备状态监测与故障诊断领域的热门研究对象［1］。针对轴承，传统的和现有的状态监测与故障诊断技术侧重于发现故障并及时修复，是基于被动的维修模式;与此不同的是，性能退化评估技术作为一种主动的维护模式，侧重于对其性能退化全过程走向的分析，而并不局限于对其某时刻的状态的诊断。通常，轴承要经过一系列的不同的性能退化状态直至完全失效。因此，如果能在轴承性能退化的过程中监测到其性能退化的程度，那么就可以有针对性地制定维护计划，从而有效地防止因轴承故障而引起的设备意外失效。

轴承振动信号是一种典型的非平稳信号［2］。小波包变换是一种典型的非平稳信号的处理方法，已广泛应用于轴承振动信号的处理中［3］。隐马尔可夫模型(HMM)能够有效地描述随机过程的统计特性，是一种强有力的模式识别方法。因此，本文提出了一种基于小波包变换和HMM的轴承性能退化评估方法。该方法使用小波包变换对轴承振动信号进行分析，并提取节点能量及其总能量作为特征，仅使用正常状态下的数据训练HMM，建立性能退化评估模型，然后以待测数据对应的模型输出，即对数似然概率值作为轴承的性能指标，从而实现对轴承退化程度的定量评估。最后，通过对轴承加速疲劳寿命试验的研究，验证了所提出的方法的可行性和有效性。

1 理论基础

1.1 小波包变换

小波包变换是小波变换的推广，它对小波变换中没有分解的高频部分进行了进一步的细分。因此，与小波变换相比，小波包变换在高频频带具有更高的频率分辨率，是一种更精细的信号处理方法。

在使用小波包变换对信号进行分解时，每个节点的信号都被分解为近似部分(低频)与细节部分(高频)，它们的分析带宽降为原节点信号的分析带宽的一半。图1所示为一个三层小波包分解树。图中，S代表原始信号，A代表近似部分，D代表细节部分。在第三层分解中，信号被分解成 AAA3、DAA3、ADA3、DDA3、AAD3、DAD3、ADD3、DDD3八个部分，它们的分析频带分别为0－Fs/16、Fs/16－2Fs/16、2Fs/16－3Fs/16、3Fs/16－4Fs/16、4Fs/16－5Fs/16、5Fs/16－6Fs/16、6Fs/16－7Fs/16、7Fs/16－8Fs/16。其中，Fs为原始信号的采样频率，Fs/2为其分析带宽。

图1 三层小波包分解树Fig.1 A 3-level wavelet packet decomposition tree

在进行模式识别前，通常还要对分解后的各节点信号进行进一步的特征提取，以减小特征向量的维数。小波包能量就是其中一种常用的特征提取方法［4］。第j层上节点k的小波包能量定义为:

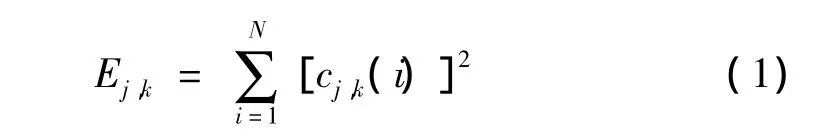
式中，cj，k(i)是第 j层上节点k的第i个小波包系数。

1.2 隐马尔可夫模型

HMM是一个双重随机过程，即不仅状态之间的转移是随机的，而且各状态下产生的观测值也是随机的。一个具有离散观测值的HMM可以用以下参数来描述［5－7］:

(1)模型状态数目N。记N个状态为S={S1，S2，…，SN}，t时刻的状态为 qt。显然，qt∈S。

(2)各状态下的观测值数目M。记M个观测值为V={V1，V2，…，VM}，t时刻的观测值为 ot。显然，ot∈V。

(3)状态转移概率矩阵A={αij}。其中:

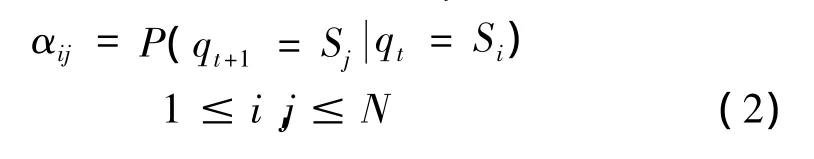
(4)观测值概率矩阵B={bj(k)}。其中:

(5)初始状态概率分布π={πi}。其中:

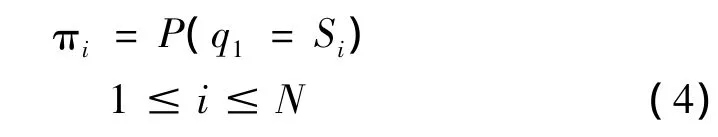
因此，一个HMM可以用N、M、A、B和π五个参数表示。为了方便，可简记为:

上面我们讨论的是离散观测值的情况，但是在实际应用中，我们常常遇到观测值是连续值的情况。虽然连续信号可以通过编码转化成离散点，但是这种编码过程可能引起信息的丢失［6］。因此，与具有离散观测值的HMM相比，具有连续观测值的HMM更具有优势。

在具有连续观测值的HMM中，通常使用高斯混合模型来拟合观测值概率分布［6］

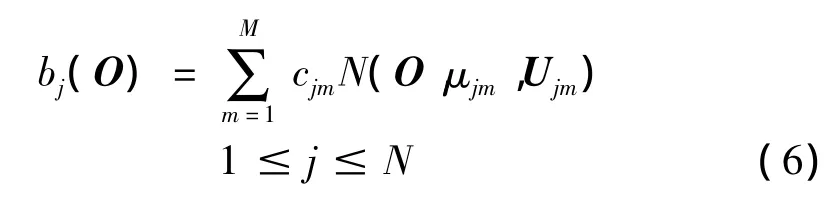
式中，M是高斯元数目，cjm是第j个状态第m个高斯元的混合系数，μjm、Ujm分别是第j个状态第m个高斯元的均值向量和协方差矩阵。因此，一个观测值概率分布为混合高斯分布的HMM可表示为:

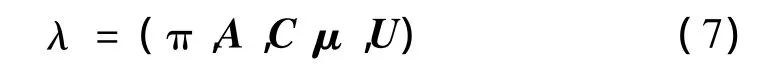
其参数可使用期望最大(EM)算法来估计，详见文献［6－7］。

1.3 性能退化评估方法

随着轴承性能的不断退化，轴承振动信号的小波包能量将偏离正常值。选取轴承正常状态下的数据训练HMM，得到正常状态下的模型λ，然后利用该模型的输出概率)来描述待测数据O偏离正常值的程度。应用小波包变换和HMM进行轴承性能退化评估的主要步骤如下(流程图如图2所示):

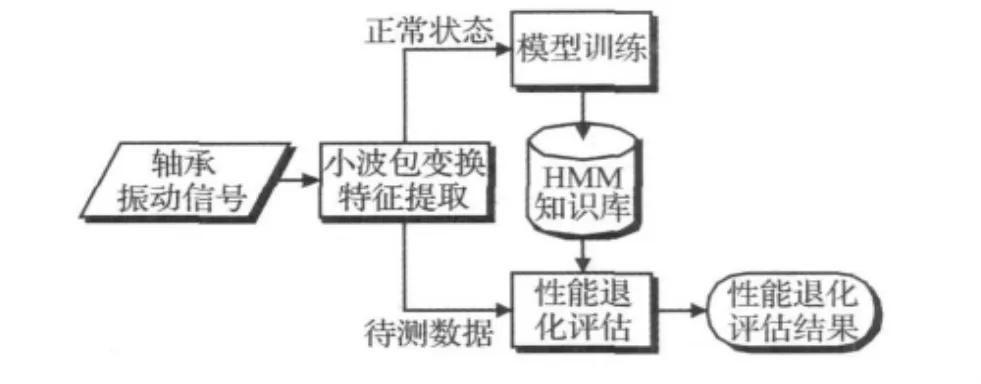
图2 性能退化评估流程图Fig.2 Performance degradation assessment scheme

(1)使用小波包变换对轴承振动信号进行分解，并提取各节点能量及其总能量组成特征向量。

(2)选取轴承正常状态下的数据作为训练数据，训练HMM，得到模型λ，建立HMM知识库。

(3)将待测数据O输入已训练好的模型λ中，计算该模型的输出概率。因为模型λ是根据正常状态下的数据训练而得的，所以)表征了正常轴承运行时产生数据O的概率，也可以说，数据O由正常轴承产生的概率。越大，则数据O由正常轴承产生的概率越大，那么，实际产生数据O的轴承处于正常状态的概率就越大;反之，轴承处于失效状态的概率就越大。因此，P(Oλ)可以用来描述轴承的性能。

2 实验研究

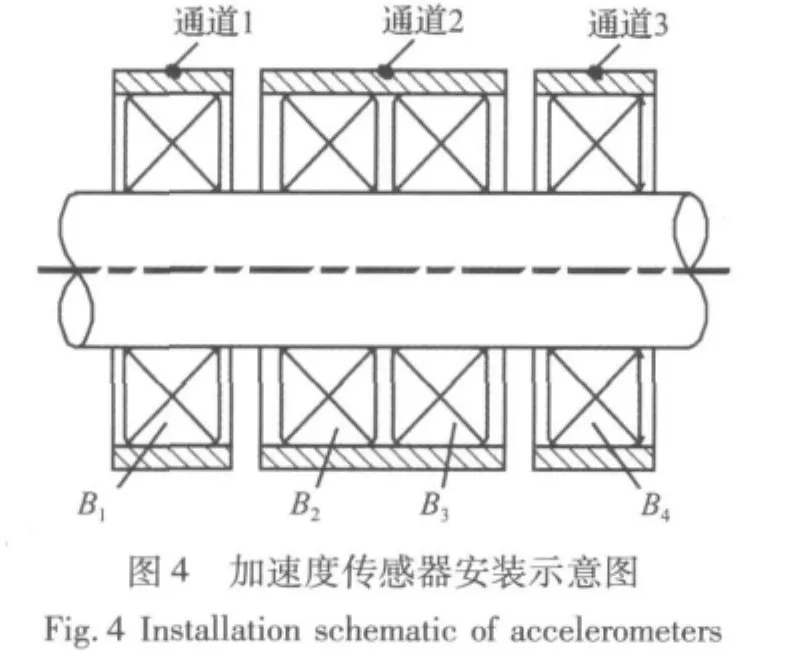
为验证所提出的方法的可行性和有效性，我们进行了轴承加速疲劳寿命试验。实验装置如图3所示。该实验装置主要由两部分组成:① 由杭州轴承试验研究中心提供的ABLT－1A型轴承寿命试验机;② 自开发的数据采集系统。该试验机最多可同时安装四个轴承进行加速疲劳寿命试验，并装有四个热电偶和一个加速度传感器，分别用于测量四个试验轴承的外圈温度和整个试验机的振动。为了分别获得各轴承的振动信号，我们还特别安装了一套自开发的数据采集系统。该系统主要包括三个加速度传感器、两个NI SCXI－1531信号调理模块、两张NI PCI－6023E多功能数据采集卡和一套基于LabVIEW 7.1开发的数据采集软件。三个加速度传感器安装示意图如图4所示。由于轴承2与轴承3共用一个轴承盖，所以此处只安装了一个加速度传感器。

在该实验中，采用6307深沟球轴承作为试验轴承。将四个正常的试验轴承安装在试验机上，加载12.744 kN，并采用油润滑。试验机转速为 3000 r/min。采样频率为 25.6 kHz，每分钟记录0.8 s的数据，即每组数据包含20480点。从开始采集直到报警停机，一共运行了2469 min，采集到了2469组数据。经检测，发现第四个轴承的内圈出现大面积的点蚀，如图5所示。因此，使用第三通道的数据进行分析。

首先，对第三通道的数据进行小波包分析。为了更详细地分析数据随时间的变化规律，先对数据进行前处理，将每组数据等分成40段，即每段512点，再对每段数据进行小波包分析。在进行小波包分析时，为了能在一个节点中监测到轴承的2～3倍故障频率的调制作用，应使最后一层各节点的分析带宽大于三倍轴承内圈故障频率，即分解层数应满足［3］

图5 试验轴承失效形式Fig.5 Failure mode of the test bearing

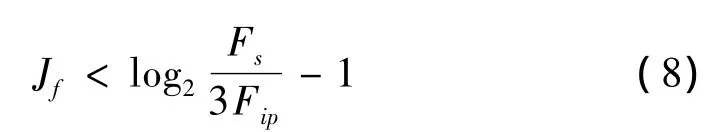
式中，Fs为采样频率，Fip为轴承内圈故障频率。6307深沟球轴承的理论内圈故障频率为246 Hz，因此，Jf＜4.12。这里采用db4小波对每组数据进行四层小波包分解，并根据式(1)提取第四层分解的各节点能量作为特征。各节点能量反映了信号在不同频带上的能量大小，其总能量反映了信号的总能量大小。因此，除各节点能量外，还将第四层分解的节点总能量作为特征。即特征向量由第四层分解的各节点能量及其总能量组成。因此，每组数据可用一个17×40的特征矩阵表示。

然后，选取轴承正常状态下的数据作为训练数据，训练HMM。取模型状态数目 N=4，高斯元数目M=2，选取前200组数据作为训练数据。以从每组数据提取出来的特征矩阵构成一条观测值序列，再用这200条观测值序列对模型进行训练。这里，为了便于推理，假设这些观测值序列之间相互独立。因此模型训练的目标是调整模型参数，使式(9)取得最大值。

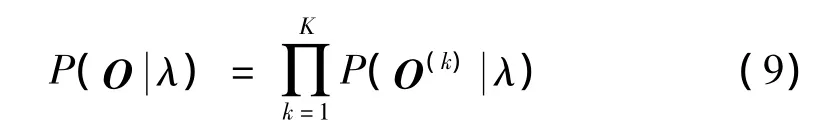
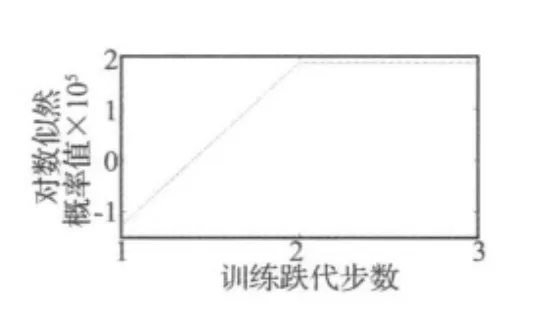
图6 训练曲线Fig.6 Training curve

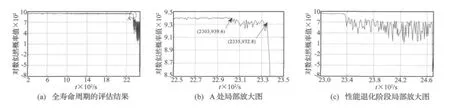
图7 性能退化评估结果Fig.7 Perfromance degradation assessment results

3 结论

鉴于小波包变换和HMM的优点，本文提出了一种基于小波包变换和HMM的轴承性能退化评估方法。最后，为了验证所提出的方法的可行性和有效性，采用6307深沟球轴承进行了加速疲劳寿命试验。轴承一共运行了2469 min，共采集了2469组数据。将每组数据等分成40段，然后对每段数据进行四层小波包分解，并提取小波包能量和其总能量组成特征向量。选取前200组数据训练HMM，然后对待测数据计算模型输出概率，并以此作为轴承的性能指标，对轴承进行性能退化评估。实验结果表明，所提出的方法能够很好地反映轴承性能的退化过程，可以为维护计划的制定提供重要的依据。

［1］Patil M S，Mathew J，RajendraKumar P K.Bearing signature analysis as a medium for fault detection:a review［J］.Journal of Tribology，2008，130(1):014001－1－7.

［2］Antoni J.Cyclic spectral analysis of rolling-element bearing signals:facts and fictions［J］. Journal of Sound and Vibration，2007，304(3－5):497－529.

［3］Nikolaou N G，Antoniadis I A.Rolling element bearing fault diagnosis using wavelet packets［J］.NDT＆E International，2002，35(3):197－205.

［4］Ekici S，Yildirim S，Poyraz M.Energy and entropy-based feature extraction for locating fault on transmission lines by using neural network and wavelet packet decomposition［J］.Expert Systems with Applications， 2008， 34(4):2937－2944.

［5］Rabiner L R，Juang B H.An introduction to hidden Markov models［J］.IEEE ASSP magazine，1986，3(1):4 －16.

［6］Rabiner L R.A tutorial on hidden markov models and selected applications in speech recognition［J］.Proceedings of the IEEE，1989，77(2):257－286.

［7］冯长建.HMM动态模式识别理论，方法以及在旋转机械故障诊断中的应用［D］.杭州:浙江大学，2002.