基于状态监测的设备寿命预测与预防维护规划研究进展

孟 光，尤明懿

(上海交通大学 机械系统与振动国家重点实验室，上海 200240)

设备能否持续高效、安全地工作，维护能否及时、有效地开展，都与一个机构、公司乃至国家的竞争力息息相关。如今，越来越复杂精巧的设备使其有效运行的可靠性成为突出问题;另一方面，竞争激烈的市场又要求设备能更可靠高效地工作。由此，高效、经济的维护策略的重要性就显而易见了。1981年，美国国内工厂针对重要设备的维护费用为6000亿美元。20年内，这一数字翻了20倍。一个更惊人的事实是，由于无效、低效的维护，有1/3至1/2的维护费用被浪费了［1］。因此，就需要不断发展与改进现有的维护策略。如今，设备维护策略已由事后维护(corrective maintenance)，基于时间的预防维护(time-based preventive maintenance)，逐步发展为基于状态的维护(conditionbased maintenance(CBM))［2］。对于维护费用的分析显示，设备失效后维护的费用往往数倍于采用CBM策略的维护费用［3］。另一份调查显示，对状态监测投入1万美元－2万美元，每年有望节省50万美元的维护费用［3］。CBM的益处不仅是维护费用的降低，还包括:设备失效时间的减少(设备可用度的提高)，库存的削减，和后勤与供应链的改善［4］。例如:美国“智能维护系统”中心(center for intelligent maintenance systems)估计，仅在美国国内，若采用CBM策略，仅因设备可用度提高这一项，每年就可节省50亿美元［5］。

CBM对维护决策的支持主要有两方面:诊断(diagnostics)与预测(prognostics)。Diagnostics致力于失效发生后的发现、隔离与鉴定;Prognostics致力于预测、防止失效的发生。虽然无法完全代替diagnostics，prognostics在预防失效发生方面更为有效。然而，相对diagnostics而言，prognostics方面的研究较少［2］。

Prognostics主要有两大方面的研究:寿命预测与预防维护规划［2］。文献［1］总结了至2008年寿命预测方面的一些工作，文献［2］总结了至2005年寿命预测和预防维护规划两大方面的主要研究。然而，一方面prognostics的研究日新月异，新的方法、模型不断涌现，需要及时总结;另一方面需要对prognostics的各种方法、模型进行分类和归纳，将有助于掌握各类方法的特点及其适用性，并发现新的研究方向。本文对目前为结、分类和简单的比较，进而探讨一些必要的、有价值的研究方向。

1 基于状态监测的寿命预测方法

基于状态监测的设备寿命预测，具体而言，是在设备A运行的某一时刻t，根据监测的(至时刻t的)设备A的运行状态和/或同类设备的历史数据，预测设备A由当前至失效的剩余寿命(residual life)(或剩余有效寿命(remaining usefullife))。这里，历史数据可以是同类设备从运行到失效过程中的状态监测数据(condition monitoring data)，可以是失效时间数据、维护时间数据等事件数据(event data)，也可以是两者的综合。Jardine等［2］将剩余寿命表述为:

式中，T为表示失效时刻的随机变量，t为当前时刻，向量Z(t)为至当前的状态数据。更全面地，可将式(1)拓展为:

式中，向量Zhj(v)为同类设备j在运行时刻ν的状态监测数据，向量Ehj为同类设备j的事件数据(尤其是失效时间，预防维护时间等数据)，u∈［0，t］，ν∈［0，Thj］，j=1，2，…，L，L表示可获得历史数据的同类设备的个数，Thj为同类设备j的最终失效或不再服役的时刻。寿命预测，既指预测变量T－t的分布，有时也指预测T－t的期望［2］，即:

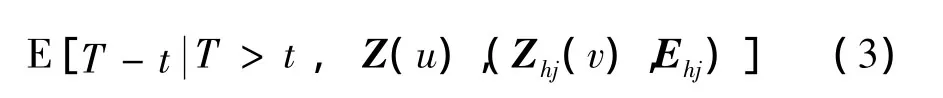
文献中，设备寿命预测的方法主要可以分为［1，2］:基于物理(第一原理)的方法和基于经验的方法，下文1.1节和1.2节总结近年来关于这两类方法的主要工作。

1.1 基于物理(第一原理)的方法

基于物理的方法试图结合:①设备特定的机械动力学知识(如:损伤增长模型);②设备在线状态监测数据，以预测设备的剩余寿命。文献中常见的基于物理的方法主要使用裂纹扩展模型，碎裂增长模型等。

Ray与Tangirala［6］提出了裂纹扩展的非线性随机模型，结合实测传感器信号估计裂纹长度、裂纹扩展速率及材料的剩余寿命。

Li等［7］提出了一个滚动轴承寿命预测的框架，该框架包括一个确定性损伤扩展模型，一个诊断模型和一个自适应算法。其中，诊断模型用于从传感性信号中估计缺陷尺寸;由此估计，损伤扩展模型可计算得缺陷扩展率，并预测下一时刻的损伤尺寸;自适应算法根据预测值和实际值的偏差在线更新损伤扩展模型的参数，这就抓住了损伤扩展的动态特性。可是，诊断模型并未予以详细讨论，在文献［7］的实验中，直接使用了实测的损伤尺寸。在后续的工作中，Li等［8］将确定性损伤扩展模型推广到随机损伤扩展模型。

Glodez等［9］提出了一个齿轮寿命的确定性计算模型，该模型以应变－寿命方法计算裂纹萌生所需的应力循环数，以Paris方程模拟裂纹扩展过程，以位移相关法计算应力强度因子与裂纹长度的函数关系，最后估计齿轮的寿命。

基于振动响应分析和损伤力学，Qiu等［10］提出了一个基于刚度的轴承系统预测模型。在文献［10］中，轴承系统作为单自由度振动系统，因此其固有频率和加速度幅值可与系统刚度相关联。另一方面，通过损伤力学，可将失效时间，服役时间和刚度变化联系起来。这样，一个轴承系统的固有频率和加速度幅值便可与失效时间和服役时间联系起来。因此，可以通过振动测量在线预测轴承系统的失效时间。

Oppenheimer和 Loparo［11］提出了一个基于物理的转轴裂纹诊断与预测方法，该方法包括监测器和寿命模型。假设可由实测信号计算轴端速度和轴端力，根据转轴的动力学模型，监测器可估计裂纹的长度。而后，寿命模型基于线弹性断裂力学Forman裂纹增长原理计算转轴的剩余寿命。

基于简化的齿轮动力学方程，Wang［12］提出了在线估计、更新齿轮啮合刚度、啮合系数的方法。而后，根据齿轮啮合刚度和啮合系数的变化就可判断齿轮的健康状态，并预测其剩余寿命。不过，文献［12］指出仍需要一个裂纹扩展模型来预测齿轮的剩余寿命。

针对飞机发动机的油湿部件，Orsagh等［13］讨论了信息融合框架，融合方法等一系列有关故障诊断和预测的概念。文献［13］中以轴承为例讨论了轴承接触失效情况下的寿命预测方法，在碎裂(spall)萌生前使用Yu-Harris模型，在碎裂萌生后则使用碎裂扩展模型。同时，文献［13］也讨论了将Yu-Harris模型和碎裂扩展模型随机化的方法，该方法考虑了载荷、不对中、润滑和制造过程中的不确定因素。

Chelidze和 Cusumano 等［14－16］将失效过程视为分级动态系统，其中损伤扩展的过程远慢于可观测的系统动态特性，并假设快速的、可观测的系统动态特性由某常微分方程控制，但并不需要知道该方程的具体模型。另一方面，若需进行寿命预测，则需要知道损伤扩展的数学模型。这方面类似的研究还有文献［17］。文献［17］可视为对文献［14－16］的进一步扩展，将状态监测数据与具体的物理模型结合以提高寿命预测的精确度。

以H－60直升机中级齿轮箱的主动齿轮为例，文献［18］将疲劳失效分为裂纹形成与裂纹扩展阶段。在裂纹形成阶段，用Neuber原理估计裂纹萌生的循环数;在裂纹扩展阶段，则使用Paris公式计算裂纹扩展至失效的循环数。(这样的思路与文献［13］中相似。)文献［18］中建议，当基于状态监测数据的裂纹长度估计模型建立后，可用该模型取代Paris公式以估计裂纹扩展至失效长度的概率分布。

Li和Lee［19］提出了一个直齿轮寿命预测方法，该方法包括一个基于有限元法的齿轮裂纹长度估计模型，一个齿轮动力学仿真器(以估计齿轮载荷)，一个计算应力强度因子的仿真器，和一个基于Paris公式的寿命预测模型。文献［19］中方法考虑了在裂纹扩展过程中，齿轮刚度变化造成的动态载荷。试验证明，该方法具有较高的预测精度。若事先将齿轮载荷与应力强度因子在各种情况下的值制成查询表，文献［19］中的方法则适用于现场应用。

Marble和Morton［20］就轴承碎裂扩展进行了一系列实验研究，他们指出碎裂形成的过程是多个小裂纹萌生和聚结的结果，而非单一主裂纹扩展的过程。因此，传统的裂纹扩展模型(例如Paris公式)并不适用于轴承。文献［20］中提出了碎裂扩展公式，结合有限元方法计算公式中需要的碎裂周围的应力，进而预测轴承寿命。同时，文献［20］也讨论了根据在线诊断结果更新模型的方法。

Ramakrishana 和 Pecht［21］根据线性损伤理论(Palmgren－Miner理论)估计印刷电路板上焊点在振动和温度载荷下的损伤累计，并以同样的方法估计焊点仅在热循环(thermal cycling)下的剩余寿命。试验结果表明，线性损伤理论能较好地估计一批样本的剩余寿命均值，但文献［21］中未讨论如何对单个样本的剩余寿命做出较好地预测。类似地，Gu等［22］用应变计检测振动载荷下印刷电路板的响应(弯曲曲率)，以解析模型进一步计算焊点的应变，然后以Miner原理估计焊点损伤的累积并预测焊点的剩余寿命。类似的研究还有文献［23］。

基于物理的寿命预测方法，由于具备设备特定的物理学模型，往往不需要大量同类设备的历史数据即可获得较精确的预测结果。但是，该方法有时需要进行停机检查［7］，这往往是不经济的甚至为生产所不允许。更重要的是，对于复杂设备，建立完备的物理学模型往往非常复杂［17］。这就催生了直接基于设备的状态监测数据，而不使用具体的物理学模型的方法:基于经验的方法。

1.2 基于经验的方法

基于经验的方法，又称数据驱动的(data-driven)方法，试图直接从状态监测数据(及同类设备的历史数据)在线预测设备的剩余寿命。对基于经验的方法，在一些文献中有进一步的分类［1］，但往往各小类之间有所重叠，如:基于状态外推的方法和基于人工智能的方法。我们认为，按照“监测状态－失效/剩余寿命”之间的不同联系，可将目前主要的基于经验的方法进一步分为:基于状态预测/外推的方法，基于统计回归的方法，和基于相似性的方法。

(1)基于状态预测/外推的方法

基于状态预测/外推的方法，认为设备失效可直接定义于状态空间，即可用确定性的失效阀值(单变量情况［24］)或失效面(多变量情况［25］)定义设备失效。在设备A运行的当前时刻t，基于状态预测/外推的方法试图预测其状态的进一步发展，并将预测的未来状态与失效阀值(或失效面)进行比较以预测设备的剩余寿命分布，并估计剩余寿命。

以一个附有张力的钢带为例，Swanson等［26］以Kalman滤波器跟踪钢带的固有频率。给定一个固有频率的失效阀值，Swanson等进而给出了预测失效时间及计算预测不确定性的模型。

Engel等［27］以多项式模型外推特征变量以预测直升机齿轮箱的剩余寿命。文献［27］中提出了以寿命预测为目标，评估多个特征变量的一种方法，而目前文献中大多数评估的方法则以故障的早期发现或故障诊断为目标。文献［27］中也指出，一个有效的寿命预测方法，不仅需要考察预期剩余寿命，也需考虑该预测的不确定性(以置信区间表达)。

Cheng和Pecht［28］讨论了将基于物理的方法和基于经验的方法融合的预测框架。其中基于物理的方法主要用于确定关键参数，确定潜在的失效机制并为其排序，确定失效模型，定义失效;基于经验的方法主要用于从监测变量中提取特征，建立健康基准，异常监测，预测参数的变化趋势等。从寿命预测的角度讲，文献［28］中的方法主要还是基于经验的。

Vachtsevanos和Wang［29］介绍了基于动态小波神经网络(dynamic wavelet neural network)的预测方法，并以一个滚动轴承为例展示了该方法的可行性。示例中，以轴承振动信号的功率谱密度(PSD)为特征变量。在预测剩余寿命时，需假设基于PSD的失效阀值。

Chinnam和Baruach［30］指出在一些情况下无法在特征变量空间定义失效(即找到确定性的失效阀值或失效面)，却可以根据专家知识(expert knowledge)或操作经验来定义失效。这样的情况下，他们建议采用focused time－lagged feed－forward神经网络预测特征变量，采用Sugeno模糊推理模型来定义失效，进而预测设备的性能可靠性。文献［30］中以钻头为例描述了其方法的可行性，但是限于其神经网络的预测步长较短而无法估计剩余寿命。但是，文献［30］中对失效定义的处理方法仍有借鉴意义，结合能进行长程预测的预测模型，可以继续探讨在此失效定义下，剩余寿命预测的精确性。

给定失效阀值，Orchard和 Vachtsevanos［31］使用粒子滤波方法预测行星载板的剩余寿命，并给出该预测的置信区间。试验结果显示文献［31］中的方法具有对系统加载条件和特征变量信噪比的“鲁棒性”。

文献［32，33］中，Gebraeel等以 Bayes方法在线更新指数衰退模型的参数，结合失效阀值得到设备剩余寿命分布的封闭形式，并将该方法应用于轴承的加速寿命试验中监测的振动幅值数据。文献［32，33］中方法的推广、改进有文献［34－36］。Gebraeel和 Pan［34］考虑了设备运行环境是时变的情形。Gebraeel等［35］考虑了同类设备历史数据中失效时间数据可得，但没有失效过程中的状态监测数据的情形。Chakraborty等［36］考虑了设备性能衰退模型的随机参数不呈正态分布的情形，发展了性能衰退模型的随机参数符合更普遍分布形式时设备剩余寿命分布的预测方法。

由以上文献可见，基于状态预测/外推的方法往往采用各类时间序列的预测方法。因此，文献中大量其他的时间序列预测方法(例如，在线支持向量回归方法，指数平滑算法等)也可以在类似的框架下应用，并可能取得更好的预测效果。

(2)基于统计回归的方法

基于统计回归的方法，认为监测的状态是影响设备失效概率的因素。该方法往往需根据同类设备的历史数据建立起“设备失效概率，设备监测状态及设备运行时间”之间的函数(简称函数B)。在设备A运行的当前时刻t，基于统计的方法一般也需预测设备状态的进一步发展，并将该预测代入函数B，进而以设备失效概率分布的期望值预测设备A的剩余寿命。相比于基于状态预测/外推的方法，基于统计回归的方法往往无需定义确定性的失效阀值。

Goode等［37］指出许多设备(如:热轧钢厂的水泵［37］)的失效过程可分为稳态过程和非稳态过程。其中，稳态过程对应于设备正常运行的阶段，而非稳态过程对应于发现故障到设备最终失效的阶段。Goode等建议用统计过程控制的方法区分这两个过程。在稳态过程，文献［37］中使用可靠性数据(即稳态过程和非稳态过程长度的分布)进行寿命预测。进入非稳态过程，文献［37］假设设备的状态监测数据呈指数型增长，并同时利用状态监测数据和可靠性数据进行寿命预测。当然，文献［37］中方法的有效性很大程度上取决于模型的假设是否成立，以及状态检测数据的质量。

Wang等［38］将专家建议(关于水泵是否需要维护)分为四等，同时假设水泵轴承与造纸机轴承的寿命分布具有相同的形状函数(shape parameter)和不同的尺度函数(scale parameter)，并以此计算水泵中关键轴承的风险函数，进而对单个水泵进行寿命预测。

Kwan等［39］提出了一个基于隐马尔科夫模型(HMM)的诊断与预测框架，并以轴承实验数据验证该框架的有效性。但是，文献［39］中认为预测主要是失效后对设备状态变化过程的估计，而并未讨论如何在设备失效前预测其剩余寿命的方法。在文献［39］的基础上，Zhang等［40］提出了轴承失效诊断与预测的集成方法，该方法包括主成分分析，HMM，和一个自适应随机预测模型。其中，用PCA提取监测信号的主要特征，用HMM诊断轴承当前的状态(即:失效类型和当前处于HMM中最终失效状态的概率(健康指标))，用自适应随机预测模型预测并更新健康指标的发展趋势，在此基础上进行寿命预测。

Baruach 和 Chinnam［41，42］也建议使用 HMM 进行诊断与预测，对设备失效过程中的每个健康状态都单独建立一个HMM，再估计每个样本的状态转变点，进而估计状态转变点的条件分布，但文献［41，42］中并未具体讨论如何预测剩余寿命。Camci和 Chinnam［43，44］将分级HMM(hierarchical HMM)视为动态贝叶斯网络进行诊断和预测。相比于文献［41，42］的方法，文献［43，44］中的方法可以直接估计设备健康状态之间的转移概率。文献［43，44］中假设每个健康状态的区间为指数分布，采用Monte Carlo仿真的方法估计设备的剩余寿命及其置信区间，并以钻头为例展示了其方法的有效性。类似的研究还有文献［45］。

Dong 和 He［46，47］指出传统的 HMM 的不足在于隐含地以指数分布刻画各健康状态的区间长度，而这往往并不符合实际。因此，就有必要明确刻画各状态的区间长度。文献［46，47］使用隐半马尔科夫模型(hidden semi－Markov model(HSMM))以克服此不足之处。在水泵试验中，HSMM较传统的HMM取得更优的状态识别率。Peng和Dong在［48］的基础上进一步考虑了状态区间长度与设备老化相关的情况，在HSMM中引入老化因子以刻画不同时刻各状态区间长度的分布。在水泵试验中，在接近水泵失效时，文献［48］中的方法较文献［46，47］中的方法能更精确地预测水泵的剩余寿命。

Yan等［49］建议使用logistic regression来建立设备的特征变量与其失效概率之间的联系，同时建议采用ARMA模型对特征变量进行预测，将预测值输入经训练的logistic模型进行剩余寿命预测。但是，文献［49］中仅给出剩余寿命预测的示意图，并未给出具体的方法。

Volk 等［50，51］建议使用比例强度模型(proportional intensity model，PIM)预测设备的寿命，并以此评价预防维护的效果。文献［51］中同时介绍了可修系统与不可修系统寿命预测的PIM。

Banjevic和 Jardine［52］使用比例风险模型(proportional hazards model，PHM)预测设备的可靠性函数与剩余寿命。文献［52］中将内部和(或)外部协变量的发展过程刻画为Markov过程，以此在某一时刻对协变量未来的发展趋势进行预测，并结合PHM预测设备的剩余寿命。文献［52］中以运输机的转动机构为例展示了方法的主要概念。但是，将协变量发展过程刻画为Markov过程往往需要对一“连续”的协变量进行区间划分，进而以有限个数的“状态”描述协变量的发展过程。区间划分的得当与否将很大程度上决定文献［52］中模型的预测效果。因此，在实际应用中，必须仔细寻找适当的区间划分方案(区间个数，各区间范围)。

以轴承为例，Liao等［53］比较了 Logistic regression方法和PHM模型在预测单个设备剩余时的表现。文献［53］中以监测振动信号的均方根值和翘度值作为PHM中的协变量进行寿命预测，试验结果表明PHM的预测精度好于Logistic regression模型。

Ghasemi等［54］认为PHM的协变量应为系统的真实状态，他们假设在一CBM计划中系统的状态不直接可见，但可以观察到一些特征信号，这些特征信号与系统状态随机相关。于是，隐马尔科夫模型(HMM)便可用于描述特征信号－系统状态的映射。在此基础上，将系统状态作为PHM的协变量用于估计系统的条件可靠性函数和预测剩余寿命。

Wang［55］假设设备的状态监测信号是其剩余寿命的函数(而与之前的状态监测信号无关)，在此基础上利用随机滤波方法(stochastic filtering)建立设备剩余寿命的概率密度函数。文献［55］中以滚动轴承为例比较了真实的剩余寿命与预测的剩余寿命分布，结果较佳。根据文献［55］的方法，Carr和 Wang［56］继而考察了系统有多个失效模式时的情况。文献［56］中指出，在系统存在多种失效模式时，识别系统的失效模式，进而根据具体失效模式建立相应的寿命预测模型相对于不考虑失效模式的广义模型能去的更高的预测精度。

Tian等［57］建议同时利用失效和删失样本的数据来训练神经网络，进而预测设备的剩余寿命。文献［57］中的神经网路，以设备的寿命(运行时间)和状态监测信号为输入，以设备的寿命百分比为输出。文献［57］中以水泵轴承的振动信号数据验证了其方法较传统的不使用删失样本的神经网络能取得更精确、可靠的预测结果。

(3)基于相似性的方法

基于相似性的方法，认为某正在服役的设备A的剩余寿命可预测为同类设备(又称参考设备)在某一时刻剩余寿命的“加权平均”。其中，权值根据设备A与各参考设备之间的相似性计算，而相似性则需进一步根据各设备在失效过程中的状态监测数据确定。相比于基于状态预测/外推的方法和基于统计回归的方法，基于相似性的方法有时无需进行状态预测。

Zio和Maio［58］提出了一个基于相似性的寿命预测方法。文献［58］中以基于模糊逻辑的“距离值”刻画①正服役系统的特征变量与②参照集中系统的特征变量之间的相似程度，进而计算权重值，并以参照集中系统的剩余寿命的加权平均预测正服役系统的剩余寿命。文献［58］以一核电系统的应用展示了改方法的有效性。试验显示，该方法具有较高的预测精度。类似的研究还有文献［59］，但文献［59］中使用了不同的刻画相似程度和加权平均剩余寿命的方法。

以上两篇文献根据监测状态直接计算相似性，也有一些文献以监测状态估计设备当前运行时间等参数，进而根据估计值与实际值之间的误差计算相似性和权重值，总结如下。

Gebraeel等［60］采用轴承的损伤频率及其六次谐波处的振动幅值为特征变量，提出两种基于神经网络的寿命预测方法，取得较佳的预测精度。两种方法中，均以历史数据(训练集)为基础建立起多个前馈反向传播神经网络，估计某正服役轴承的服役时间，进而根据各神经网络对服役时间的预测误差确定权重值。不同的是，第一种方法将正服役轴承的寿命计算为训练集中各轴承寿命的加权平均;第二种方法则以加权平均的方法估计服役轴承指数性能衰减模型的参数，以进一步计算轴承寿命。文献［60］中以一振动幅值的阀值来定义轴承失效。

Huang等［61］提出了一个基于自组织映射(self－organizing map)的振动信号特征提取方法，在此基础上以文献［61］中的神经网络方法预测球轴承的服役时间，进而预测其剩余寿命。

Gebraeel和 Lawley［62］使用前馈反向转播神经网络估计轴承特征变量指数衰退模型的参数，结合失效阀值预测轴承的失效时间。同时，文献［62］中以Bayes方法依据某轴承的在线特征变量更新剩余寿命的分布。与其他两类不使用更新的基准方法比较，文献［62］中方法的平均预测误差较小。

2 基于状态监测的预防维护规划模型

Prognostics的目的就是要为维护方案的制定提供决策支持(decision support)［2］。因此，很自然地，需要在设备状态预测的过程中考虑下一步的维护方案。上一部分中总结的设备寿命预测的方法提供了设备剩余寿命的估计，而维护规划主要是在此基础上进一步确定恰当的执行维护的时间。可见，比起寿命预测，维护规划更直接地决定了维护策略的有效与否，更直接地影响了一个企业的产能。但是，维护规划问题往往较寿命预测更为复杂。总结目前相关文献，一个预防维护规划模型一般包含五大因素，即:

① 目标，如:维护费用最小化，维护费用率最小化，系统平均可用度最大化等;

② 维护方案，刻画了维护执行的特点(框架)，如:周期性(periodic)维护，顺序型(sequential)维护，控制限度(control－limit)维护等;

③ 维护质量(或维护效果)，刻画了维护行动将设备性能提升的程度，有:修复如新(perfect maintenance)，修复非新(imperfect maintenance)，修复如旧(minimal maintenance)等;

④ 退化模型，刻画了设备退化的过称，有:传统的寿命分布(lifetime distribution)，Gamma过程，马尔科夫过程等;

⑤ 维护限制，如:部件间的维护冲突，维护零件有限等。

下面总结近年来主要的相关模型。基于状态监测的维护规划模型分类方法多样，例如，Jardine等［2］将之分为完全可见系统和部分可见系统。其中，对于完全可见系统，状态监测变量完全体现了系统的真实状态;对于部分可见系统，状态监测变量不能完全体现系统的真实状态，但与之相关。我们将各种维护规划模型分类为离线预防维护规划模型和在线预防维护规划模型。

2.1 离线预防维护规划模型

离线预防维护规划模型指依据反映系统群体特征的衰退信息建立的维护模型。维护策略一旦确定(如:确定最优维护状态阀值)，并不随某一实际运行设备的实时监测数据改变。在应用离线预防维护规划模型时，某一实际运行设备的状态监测数据往往用于观测其状态值是否达到了先前确定的最优维护状态阀值。若未达到，则允许设备继续运行;一旦达到，则执行预防维护。目前文献中的离线预防维护规划模型，主要使用的估计设备失效概率的衰退模型有:PHM，几类随机衰退/损伤累计模型，马尔科夫衰退过程等。

(1)基于PHM的离线预防维护规划模型

Makis和Jardine［63］假设系统的失效概率不仅依赖于其工作时间(age)也依赖于一诊断随机过程(diagnostic stochastic process)，并使用PHM描述系统的失效概率，在此基础上建立了一个替换策略以最小化长期期望费用率。文献［63］中，Makis和Jardine假设只在离散时刻可以观察到系统诊断随机过程的值，并以阶跃函数近似计算离散观测点间的随机过程。

Kumar和 Westberg［64］提出了一个基于状态监测的替换策略。其中，用PHM确定系统失效是否与监测变量有关，进一步使用PHM估计系统的可靠性，在此基础上建立系统的预防维护模型以求取最优替换时刻。值得指出的是，文献［64］中的监测变量指的是压力等常值环境变量。

Banjevic等［65］考察了一个基于状态监测的控制限度替换策略，以最小化长期期望费用率。文献［65］中以PHM估计系统的失效率，同时假设监测的状态符合非齐次Markov过程，进而估计系统的失效概率以估计长期期望费用率，最后求得最优维护限度。文献［65］中也讨论了收集、预处理和使用实际油样、振动信号的一些经验。类似的基于PHM的替换策略及其应用还有文献［66－69］。

Ghasemi等［70］提出了一个基于周期状态监测的替换模型以最小化长期期望费用率。文献［70］中考察了监测变量不能直接反映系统真实状态，但与系统状态随机相关的情况，以PHM估计系统的失效概率，进而建立系统费用率模型。Ghasemi等［71］在文献［70］的基础上进一步考察了非周期监测的情况。

(2)基于随机衰退/损伤累计模型的离线预防维护规划模型

Barbera等［72］提出了一个基于状态检测的预防维护模型，以最小化长期期望费用。在该模型中，预防维护在系统状态值达到某一阀值时进行，并且预防维护可完全恢复系统的状态。文献［72］中假设系统的状态为非减函数，在任一时刻，系统损伤的增长为一与累计损伤无关，且概率密度函数已知的随机变量，同时系统的可靠性为系统状态的指数函数。在文献［73］中，使用与文献［72］中类似的建模方法，Barbera等又考查了一个由两个串联部件组成的系统级维护模型。Shahanaghi等［74］在文献［72］的基础上考察了修复非新的情况，认为修复后系统的状态随机地处于全新与修复前的状态之间。

Aven［75］以计数过程方法建立了一个基于状态监测的替换策略，以最小化长期期望费用率。在文献［75］的模型中，预防维护在系统失效率达到某一阀值时进行，替换之后系统恢复全新的状态。文献［75］中假设在某一时刻系统的失效率是其状态的确定性函数，但并未做具体的讨论。

Hontelez等［76］考察了漂移衰退过程的基于状态监测的维护策略以最小化一段时间内的平均维护费用。文献［76］中将漂移衰退过程分成(N+1)段，并建模成马尔科夫过程。文献［76］中使用控制控制限度维护策略，假设维修之后系统恢复全新的状态，确定了最优监测时间间隔与最优维修时间。类似的研究有文献［77］。

Wang［78］提出了一个基于状态监测的替换模型。文献［77］中基于随机参数增长模型估计系统在某一时刻的失效概率，在此基础上进行建模，进而确定最优监测区间和最优维护限度，以优化系统的长期期望费用率，失效时间率或可靠性。

Grall等［79］提出了一个针对随机衰减系统的基于状态监测的替换模型，求取最优维护阀值和最优监测时间间隔，以最小化系统的长期期望费用率。文献［79］中假设系统的状态衰退在任一时刻非负，且状态衰退增长程度的概率密度函数已知，同时系统的确定性失效阀值已知，在此基础上估计系统在某一时刻的失效概率。值得指出的是，文献［79］中考虑了监测时间间隔非常数的情况，根据系统的状态实时地确定下一个最优监测时间间隔。类似的研究还有文献［80－83］。文献［79］的基础上的进一步的研究有文献［84］。Deloux等［84］考察了单部件系统存在两种失效形式的情况，其中一种为累计损伤失效，另一种为应力环境下的冲击失效，进而优化系统长期期望费用率。Zhao等［85］考察了系统状态非单调衰退且受环境因素影响的情况下的最优监测、替换策略，以最小化长期期望费用率。文献［85］中以类似PHM的方式刻画环境因素对系统状态衰退的影响。

Nakagawa和Ito［86］考察了多部件系统的情况，他们假设系统受到的外界的随机冲击(各冲击间隔长度符合同一概率函数，各冲击造成的损伤大小而造成损伤累积符合同一概率函数)，当累积的损伤超过一定值时系统失效。在次基础上，他们建立了系统预防维护模型，计算最优维护阀值(累积损伤值)以最小化长期期望费用率。

Wang等［87］提出一个基于状态监测的订货－替换模型，考虑了维修部件需提前预定的情况。文献［87］中假设系统衰退符合随机衰退模型，衰退增量单调递增，各时刻增量互相独立且符合同样的统计分布。文献［87］中考察了系统的长期期望费用率，预防替换率和系统平均可用度指标，根据这些指标以优化订货限度，预防替换限度和监测周期长度。Wang等［88］考察了基于马尔科夫衰退过程的预防替换模型及另一种库存机制。Wang等［89］在文献［87］的基础上考察了系统失效阀值不确定的情况。

Liao等［90］提出了一个连续监测的单部件系统的预防维护模型，寻找最优控制限度(定义于系统的状态空间)以最大化系统平均可用度。文献［90］中基于随机衰退模型(如Gamma过程)计算系统的失效概率，认为系统在预防维护后的状态分布于全新与修复前的状态之间，且其密度符合某概率函数。

(3)基于马尔科夫衰退过程的离线预防维护规划模型

Marseguerra等［91］考察了一个多部件串并联系统的基于状态监测的维护模型。该模型以同时优化系统利润与可用度为目标，在系统的马尔科夫衰退模型中考虑了非完全维护因素，以遗传算法确定各部件的最优维护状态阀值。为了描述更复杂的情况，如系统衰退与外界载荷相关，维护人员有限等情况，文献［91］又建议使用Monte Carlo仿真的方法。在系统马尔科夫衰退模型已建立的情况下，文献［90］中模型针对的主要是系统设计阶段，而未考虑实际运行中对某一个系统的实时维护。类似的研究还有文献［92］，但文献［92］中采用最小化一段时间内的期望费用为目标，并采用随机衰退模型。

基于一个连续 －离散随机衰退模型，Makis和Jiang［93］提出了一个基于状态监测的优化框架以最小化长期期望费用率。文献［93］中，隐藏的设备状态发展由连续马尔科夫过程描述，监测变量与设备状态有关且由离散随机过程描述。

(4)其他

Zhou等［94］提出了一个基于状态监测的单部件系统可靠性限度维护策略，以最小化长期期望费用率。文献［94］通过混合概率模型刻画修复非新的预防维护效果。但文献［94］中未详述如何刻画系统的衰退过程以求取其在某一时刻的失效概率，未考虑到实时运行系统失效概率的动态特性。

Camci［95］提出了一个多部件系统的基于状态监测的维护模型，考虑了一些维护限制(如部件之间的维护冲突，维护资源有限等)，以最小化一段时间内的系统期望维护费用。文献［95］指出，由于系统各部件之间的联系，优化各部件的维护策略不一定导致最优系统维护策略，因此就有必要进行系统级的维护时序规划。但是，文献［95］中假设系统的失效概率已知，并未考虑实际运行系统不断变化的状态。类似的研究还有文献［96］。

2.2 在线预防维护模型

与离线预防维护模型不同，在线预防维护模型依据某一实际运行系统的在线状态监测数据不断更新最优预防维护策略，并在恰当的时机执行预防维护。在线预防维护模型针对每个设备制定不同的预防维护策略，而在离线预防维护模型中所有设备均使用同一预防维护策略。

Christer等［97］发展了一个感应电炉的感应器的替换策略。文献［97］中，由于感应电炉的结构限制，感应器裂纹的尺寸无法直接测量，文献［97］使用可以测量的“传导率”为特征变量，通过状态空间模型估计实际裂纹尺寸。文献［97］中采用卡尔曼滤波方法预测和更新感应器的失效概率，在此基础上计算最优替换时间，以最小化期望费用率。

Pedregal和 Carnero［98］描述了一个案例研究，对一个石油厂的离心压缩机进行基于状态监测的维护，以最小化长期期望费用率。文献［98］中考虑修复如新的情况，对离心压缩机上两个位置的振动信号进行状态空间建模，并以循环算法(如卡尔曼滤波器，固定区间平滑(fixed interval smoothing))预测振动信号，估计系统的失效概率，进而建立系统的费用率模型。类似的模型有文献［99］。

Kaiser和 Gebraeel［100］以文献［32］中的衰减模型为基础，提出了一个在线预测维策略文献，根据系统在线衰减信号不断更新衰减模型进而更新对系统剩余寿命的预测。文献［100］中假设维护后系统状态恢复全新，提出了一个基于系统在线可靠性的更新停止指标，从而实时地确定进行预防维护的时间。在一个制造工厂仿真试验中，Kaiser和Gebraeel比较了① 文献［100］中提出的维护策略;② 传统的基于可靠性的预防维护策略;③ 基于群体衰退模型(未根据某一系统在线衰退信号进行更新)的预防维护策略，结果表明在文献［100］中的策略下，预防维护的总费用最低。但是，文献［100］中并未考虑维护策略的优化。类似的研究有文献［101］，文献［101］中使用神经网络在线估计设备的失效概率。

3 研究方向讨论

在总结当前主要的寿命预测方法和预防维护规划模型的基础上，我们提出以下几点有必要的、有价值的研究方向:

(1)基于相似性的寿命预测方法是新近兴起的寿命预测方法。该方法可以进行长程预测，同时不需要对设备衰退信号本身进行建模，是一种简便、有效的寿命方法。但是，相关的研究还很少，针对该方法核心因素(如:相似性测度函数，权重函数)的研究很少。因此，可开展针对该方法各核心因素的比较、优化研究。

(2)总结当前基于状态监测的预防维护模型，可以看出，大多数模型是离线模型，并不随某一实际运行系统的实时信号相应更新，在线模型很少。文献［100］中的研究指出，相比于离线模型，在线模型可以取得更好的表现(如:更低的维护费用)。因此，深入开展在线预测维护模型的研究很有必要，特别是当前在线预测维护模型均未考虑常见的修复非新的预防维护效果(不完全修复)。此外，多部件复杂系统在线预测模型更少。

(3)目前寿命预测和预防维护规划的研究比较独立，作为prognostics的两个方面，两者间的结合也是值得研究的方向，如:寿命预测方法与传统的基于寿命分布的预防维护规划模型的结合，寿命预测方法与在线预测维护模型的结合等。

(4)在寿命预测和预防维护规划研究中，考察环境因素(如:温度，湿度，外界压力等)对设备衰退特性的影响(进而对寿命预测方法和预防维护规划模型的影响)是近来逐步引起重视的一个问题。然而，这方面的研究还处在初步阶段［34，85，102，103］。因此，开展这方面的研究，特别是结合试验数据定量地刻画环境因素对设备性能衰退的影响并进行建模，是很有价值的。

(5)无论是离线维护模型，还是在线维护模型［97，98］，针对基于状态监测的预防维护规划模型和传统的基于寿命分布的预防维护规划模型的比较研究很少。然而，这样的比较研究对论证基于状态监测的预防维护策略的有效性很重要。因此，很有必要开展基于一个实际系统的，针对上述两类维护策略的比较研究。

4 结束语

CBM的研究方兴未艾，作为其重要部分的prognostics的研究更是层出不穷。本文对近年来主要的寿命预测方法和预防维护规划模型进行总结、分类和简单的比较，并探讨了一些潜在的研究方向。目前，对prognostics中各方法定量的比较研究尚较缺乏，大型、复杂系统的案例研究很少。要真正将prognostics的各种方法和模型运用到实践之中，从中受益，尚需做大量的工作。

［1］Heng A，Zhang S，Tan A C C，et al.Rotating machinery prognostics:state of the art，challenges and opportunities［J］.Mechanical Systems and Signal Processing，2009，23(3):724－739.

［2］Jardine A K S，Lin D，Banjevic D.A review on machinery diagnostics and prognostics implementing condition-based maintenance ［J］. Mechanical Systems and Signal Processing，2006，20(7):1483－1510.

［3］Saranga H，Knezevic J.Reliability prediction for conditionbased maintenance systems［J］.Reliability Engineering and System Safety，2001，71(2):219 －224.

［4］Camci F.Process monitoring，diagnostics and prognostics using support vector machines and hidden Markov models［D］.Detroit:Wayne State University，2005.

［5］Harbor Research Pervasive Internet Report.Approaching zero downtime:the Center for Intelligent Maintenance Systems［R］.2003.

［6］Ray A，Tangirala S.Stochastic modeling of fatigue crack dynamics for on-line failure prognostics ［J］. IEEE Transactions on Control System Technology，1996，4(4):443－451.

［7］Li Y，Billington S，Zhang C，et al.Adaptive prognostics for rolling element bearing condition［J］.Mechanical Systems and Signal Processing，1999，13(1):103－113.

［8］Li Y，Kurfeess T R，Liang S Y.Stochastic prognostics for rolling element bearings［J］.Mechanical Systems and Signal Processing，2000，14(5):747－762.

［9］Glodez S，Sraml M，Kramberger J.A computational model for determination of service life of gears［J］.International Journal of Fatigue，2002，24(10):1013 －1020.

［10］Qiu J.Damage mechanics approach for bearing lifetime prognostics［J］.Mechanical Systems and Signal Processing，2002，16(5):817－829.

［11］Oppenheimer C H，Loparo K A.Physically based diagnosis and prognosis of cracked rotor shafts［J］.Proceedings of SPIE.2002:122－132.

［12］Wang W.Towards dynamic model-based prognostics for transmission gears ［J］. Proceedings of SPIE，2002:157－167.

［13］Orsagh R F，Sheldon J，Klenke C J.Prognostics/Diagnostics for gas turbine engine bearings［J］.ASME，International Gas Turbine Institute， Turbo Expo(Publication)ICTI，2003:159－167.

［14］Chelidze D，Cusumano J P，Chatterjee A.A dynamical systems approach to damage evolution tracking，part 1:description and experimental application［J］.Journal of Vibration and Acoustics，Transactions of the ASME，2002，124(2):250－257.

［15］Cusumano J P，Chelidze D，Chatterjee A.A dynamical systems approach to damage evolution tracking，part 2:model-based validation and physical interpretation ［J］.Journal of Vibration and Acoustics，Transactions of the ASME，2002，124(2):258－264.

［16］Chelidze D.A dynamic systems approach to failure prognosis［J］.Journal of Vibration and Acoustics，Transactions of the ASME，2004，126(1):2－8.

［17］Luo J，Pattipati K R，Qiao L，et al.Model-based prognostic techniques applied to a suspension system ［J］.IEEE Transactions on Systems，Man，and Cybernetics-Part A:Systems and Humans，2008，38(5):1156－1168.

［18］Kacprzynskl G J， Sarlashkar A， Roemer M J， et al.Predicting remaining life by fusing the physics of failure modeling with diagnostics［J］.JOM，2004，56(3):29－35.

［19］Li C J，Lee H.Gear fatigue crack prognosis using embedded model，gear dynamic model and facture mechanics ［J］.Mechanical Systems and Signal Processing，2005，19(4):836－846.

［20］Marble S，Morton B P.Predicting the remaining life of propulsion system bearings［J］.Proceedings of the 2006 IEEE Aerospace Conference，2006.

［21］Ramakrishnan A，Pecht M G.A life consumption monitoring methodology for electronic systems［J］.IEEE Transactions on Components and Packaging Technologies，2003，26(3):625－634.

［22］Gu J，Barker D，Pecht M.Prognostics implementation of electronics under vibration loading［J］.Microelectronics Reliability，2007，47(12):1849－1856.

［23］Musallam M，Johnson C M，Yu C，et al.In-service life consumption estimation in power modules［J］.200813thInternational Power Electronics and Motion Control Conference，2008:76－83.

［24］Lu H， Kolarik W J， Lu S S. Real-time performance reliability prediction ［J］.IEEE Transactions on Reliability，2001，50(4):353－357.

［25］Lu S， Lu H， Kolarik W J. Multivariate performance reliability prediction in real-time［J］.Reliability Engineering and System Safety，2000，72(1):39－45.

［26］Swanson D C，Spencer J M，Arzoumanian S H.Prognostic modeling of crack growth in a tensioned steel band ［J］.Mechanical Systems and Signal Processing，2000，14(5):789－803.

［27］Engel S J，Gilmartin B J，Bongort K，et al.Prognostics，the real issues involved predicting life remaining［J］.IEEE Aerospace Conference Proceedings，2000，6:457 －470.

［28］Cheng S，Pecht M.A fusion method for remaining useful life prediction of electronic products ［J］. 2009 IEEE International Conference on Automation Science and Engineering，2009:102 －107.

［29］Vachtsevanos G，Wang P.Fault prognosis using dynamic wavelet neural networks［J］.Autotestcon(Proceedings)，2001，857－870.

［30］Chinnam R B， Baruah P. A neuro-fuzzy approach for estimating mean residual life in condition-based maintenance systems［J］.International Journal of Materials and Product Technology，2004，20(1－3):166－179.

［31］Orchard M E， Vachtsevanos G J. A particle filtering approach for on-line failure prognosis in a planetary carrier plate［J］.International Journal of Fuzzy Logic and Intelligent Systems，2007，7(4):221－227.

［32］Gebraeel N Z，Lawley M A，Li R，et al.Residual-life distributions from component degradation signals:a Bayesian approach［J］.IIE Transactions，2005，37(6)，543－557.

［33］Gebraeel N Z.Sensory-updated residual life distributions for components with exponential degradation patterns［J］.IEEE Transactions on Automation Science and Engineering，2006，3(4):382－393.

［34］Gebraeel N Z，Pan J.Prognostic degradation models for computing and updating residual life distributions in a timevarying environment［J］.IEEE Transactions on Reliability，2008，57(4):539－550.

［35］Gebraeel N Z，Elwany A，Pan J.Residual life predictions in the absence of prior degradation knowledge［J］.IEEE Transactions on Reliability，2009，58(1):106－116.

［36］Chakraborty S，Gebraeel N Z，Lawley M，et al.Residual-life estimation for components with non-symmetric priors［J］.IIE Transactions，2009，41(4)，372－387.

［37］Goode K B，Moore J，Roylance B J.Plant machinery working life prediction method utilizing reliability and conditionmonitoring data ［J］.Proceedings of the Institution of Mechanical Engineers，2000，214(2):109 －122.

［38］Wang W，Scarf P A，Smith M A J.On the application of a model of condition-based maintenance［J］.The Journal of the Operational Research Society， 2000， 51(11):1218－1227.

［39］Kwan C，Zhang X，Xu R，et al.A novel approach to fault diagnostics and prognostics［J］.Proceedings of the 2003 IEEE International Conference on Robotics＆ Automation，2003:604－609.

［40］Zhang X，Xu R，Kwan C，et al.An integrated approach to bearing fault diagnostics and prognostics［J］.Proceedings of the American Control Conference，2005，4:2750－2755.

［41］Chinnam R B， Baruah P.Autonomous diagnostics and prognostics through competitive learning driven HMM-based clustering［J］. Proceedings of the International Joint Conference on Neural Networks，2003，4:2466 －2471.

［42］Chinnam R B， Baruah P. HMMs for diagnostics and prognostics in machining processes［J］.International Journal of Production Research，2005，43(6):1275－1293.

［43］Camci F，Chinnam R B.Hierarchical HMMs for autonomous diagnostics and prognostics［J］.2006 International Joint Conference on Neural Networks，2006:2445 －2452.

［44］Camci F， Chinnam R B. Health-state estimation and prognostics in machining processes［J］.IEEE Transactions on Automation Science and Engineering，to be published.

［45］Chinnam R B，Baruah P. Autonomous diagnostics and prognostics in machining processes through competitive learning driven HMM-based clustering［J］.International Journal of Production Research， 2009， 47(23):6739－6758.

［46］Dong M， He D. Hidden semi-Markov model based methodology for multi-sensor equipment health diagnosis and prognosis［J］.European Journal of Operational Research，2007，178(3):858－878.

［47］Dong M，He D.A segmental hidden semi-Markov model(HSMM)based diagnostics and prognostics framework and methodology ［J］. Mechanical Systems and Signal Processing，2007，21(5):2248－2266.

［48］Peng Y，Dong M.A prognosis method using age-dependent hidden semi-Markov model for equipment health prediction［J］.Mechanical System and Signal Processing，to be published.

［49］Yan J，Kog M，Lee J.A prognostic algorithm for machine performance assessment and its application［J］.Production Planning＆ Control，2004，15(8):796－801.

［50］Volk P J.Dynamic residual life estimation of industrial equipment based on failure intensity proportions［D］.Pretoria:University of Pretoria，2001.

［51］Volk P J，Wnek M，Zygmunt M.Utilising statistical residual life estimates of bearings to quantify the influence of preventive maintenance actions［J］.Mechanical Systems and Signal Processing，2004，18(4):833 －847.

［52］Banjevic D，Jardine A K S.Calculation of reliability function and remaining useful life for a Markov failure time processes［J］.IMA Journal of Management Mathematics，2006，17(2):115－130.

［53］Liao H，Zhao W，Guo H.Predicting remaining useful life of an individual unit using proportional hazards model and logistic regression model［J］.Proceedings-Annual Reliability and Maintainability Symposium，2006:127－132.

［54］Ghasemi A，Yacout S，Ouali M S.Evaluating the reliability function and the mean residual life for equipment with unobservable states［J］.IEEE Transactions on Reliability，2010，59(1):45－54.

［55］Wang W.A model to predict the residual life of rolling element bearings given monitored condition information to date［J］.IMA Journal of Management Mathematics，2002，13(1):3－16.

［56］Carr M J，Wang W.Modeling failure modes for residual life prediction using stochastic filtering theory ［J］. IEEE Transactions on Reliability，to be published.

［57］Tian Z，Wong L，Safaei N.A neural network approach for remaining useful life prediction utilizing both failure and suspension histories［J］.Mechanical Systems and Signal Processing，2010，24:1542－1555.

［58］Zio E，Maio F D.A data-driven fuzzy approach for predicting the remaining useful life in dynamic failure scenarios of a nuclear system ［J］.Reliability Engineering and System Safety，2010，95(1):49－57.

［59］Wang T， Yu J， Siegel D， et al. A similarity-based prognostics approach for remaining useful life estimation of engineered systems［C］. International Conference on Prognostics and Health Management，2008.

［60］Gebraeel N Z，Lawley M，Liu R，et al.Residual life predictions from vibration-based degradation signals:a neural network approach ［J］.IEEE Transactions on Industrial Electronics，2004，51(3):694 －700.

［61］Huang R，Li L，Xi L，et al.Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods［J］.Mechanical Systems and Signal Processing，2007，21(1):193－207.

［62］Gebraeel N Z，Lawley M A.A neural network degradation model for computing and updating residual life distributions［J］. IEEE Transactions on Automation Science and Engineering，2008，5(1):154－163.

［63］Makis V，Jardine A K S.Optimal replacement in the proportional hazards model ［J］.INFOR Journal，1992，30(2):172－183.

［64］Kumar D，Westberg U.Maintenance scheduling under age replacement policy using proportional hazards model and TTT-plotting ［J］.European Journal of Operational Research，1997，99(3):507－515.

［65］Banjevic D，Jardine A K S，Makis V，et al.A control-limit policy and software for condition-based maintenance optimization［J］.INFOR Journal，2001，39(1):32 －50.

［66］Jardine A K S，Banjevic D，Makis V.Optimal replacement policy and the structure of software for condition-based maintenance ［J］. Journal of Quality in Maintenance Engineering，1997，3(2):109－119.

［67］Jardine A K S，Banjevic D.Optimizing a mine haul truck wheel motor's condition monitoring program:use of proportional hazards modeling［J］.Journal of Quality in Maintenance Engineering，2001，7(4):286－301.

［68］Lin D，Wiseman M，Banjevic D，et al.An approach to signal processing and condition-based maintenance for gearboxes subject to tooth failure［J］.Mechanical Systems and Signal Processing，2004，18(5):993－1007.

［69］Lin D， Banjevic D， Jardine A K S. Using principal components in a proportional hazards mode with applications in condition-based maintenance［J］.Journal of Operational Research Society，2006，57(8):910－919.

［70］Ghasemi A，Yacout S，Ouali M S.Optimal condition based maintenance with imperfect information and the proportional hazards model［J］.International Journal of Production Research，2007，45(4):989－1012.

［71］Ghasemi A，Yacout S，Ouali M S.Optimal replacement policy and observation interval for CBM with imperfect information［J］.Proceedings of the World Congress on Engineering and Computer Science，2007.

［72］Barbera F， Schneider H， Kelle P. A condition based maintenance model with exponential failures and fixed inspection intervals［J］.Journal of Operational Research Society，1996，47(8):1037－1045.

［73］Barbera F，Schneider H，Watson E.A condition based maintenance model for a two-unit series system ［J］.European Journal of Operational Research，1999，116(2):281－290.

［74］Shahanaghi K，Babaei H，Bakhsha A，et al.A new condition based maintenance model with random improvements on the system after maintenance actions:optimizing by Monte Carlo simulation ［J］.World Journal of Modelling and Simulation，2008，4(3):230－236.

［75］Aven T.Condition based replacement policies-a counting process approach［J］.Reliability Engineering and System Safety，1996，51(3)，275－281.

［76］Hontelez J A M，Burger H H，Wijnmalen D J D.Optimum condition-based maintenance policies for deteriorating systems with partial information［J］.Reliability Engineering and System Safety，1996，51(3):267－274.

［77］Maillart L M.Maintenance policies for systems with condition monitoring and obvious failures［J］.IIE Transactions，2006，38(6):463－475.

［78］Wang W.A model to determine the optimal critical level and the monitoring intervals in condition-based maintenance［J］.International Journal of Production Research，2000，38(6):1425－1436.

［79］Grall A， Berenguer C， Dieulle L. A condition-based maintenance policy for stochastically deteriorating systems［J］.Reliability Engineering and System Safety，2002，76(2):167－180.

［80］Castanier B，Berenguer C，Grall A.A sequential conditionbased repair/replacement policy with non-periodic inspections for a system subject to continuous wear［J］.Applied Stochastic Models in Business and Industry，2003，19(4):327－347.

［81］Castanier B，Berenguer C，Grall A.A condition-based maintenance policy with non-periodic inspections for a twounit series system ［J］.Reliability Engineering and System Safety，2005，87(1):109 －120.

［82］Dieulle L，Berenguer C，Grall A，etal.Sequentialconditionbased maintenance scheduling for a deteriorating system［J］.European Journal of Operational Research，2003，150(2)，451－461.

［83］Grall A，Dieulle L，Berenquer C，et al.Continuous-time predictive maintenance scheduling for a deteriorating system［J］.IEEE Transactions on Reliability，2002，51(2):141－150.

［84］Deloux E，Castanier B，Berenguer C.Predictive maintenance policy for a gradually deteriorating system subject to stress［J］.Reliability Engineering and System Safety，2009，94(2):418－431.

［85］Zhao X，Fouladirad M，Berenguer C，et al.Condition-based inspection/replacement policies for non-monotone deteriorating systems with environmental covariates ［J］.Reliability Engineering and System Safety， 2010， 95:921－934.

［86］Nakagawa T，Ito K.Optimal maintenance policies for a system with multiechelon risks［J］.IEEE Transactions on Systems， Man， and Cybernetics-Part A:Systems and Humans，2008，38(2):461 －469.

［87］Wang L， Chu J， Mao W. A condition-based orderreplacement policy for a single-unit system ［J］.Applied Mathematical Modelling，2008，32(11):2274－2289.

［88］Wang L，Chu J，Mao W.An optimum condition-based replacement and spare provisioning policy based on Markov chains［J］.Journal of Quality in Maintenance Engineering，2008，14(4):387－401.

［89］Wang L，Chu J，Mao W.A condition-based replacement and spare provisioning policy for deteriorating systems with uncertain deterioration to failure［J］.European Journal of Operational Research，2009，194(1):184－205.

［90］Liao H， Elsayed E A， Chan L Y. Maintenance of continuously monitored degradation systems［J］.European Journal of Operational Research， 2006， 175(2):821－835.

［91］Marseguerra M，Zio E，Podofillini L.Condition-based maintenance optimization by means of genetic algorithms and Monte Carlo simulation［J］.Reliability Engineering and System Safety，2002，77(2):151－166.

［92］Barata J，Soares C G，Marseguerra M，et al.Simulation modeling of repairable multi-component deteriorating systems for on condition'maintenance optimization［J］.Reliability Engineering and System Safety，2002，76(3):255－264.

［93］Makis V，Jiang X.Optimal Replacement under partial observations［J］.Mathematics of Operations Research，2003，28(2):382－294.

［94］Zhou X，Xi L，Lee J，Reliability-centered predictive maintenance scheduling for a continuously monitored system subject to degradation［J］.Reliability Engineering and System Safety，2007，92(4):530－534.

［95］Camci F.System maintenance scheduling with prognostics information using genetic algorithm［J］.IEEE Transactions on Reliability，2009，58(3):539－552.

［96］Yang Z，Djurdjanovic D，Ni J.Maintenance scheduling in manufacturing systems based on predicted machine degradation ［J］.Journal of Intelligent Manufacturing，2008，19(1):87－98.

［97］Christer A H，Wang W，Sharp J M.A state space condition monitoring model for furnace erosion prediction and replacement［J］. European Journal of Operational Research，1997，101(1):1－14.

［98］Pedregal D J，Carnero M C.State space models for condition monitoring:a case study.Reliability Engineering and System Safety，2006，91(2):171－180.

［99］Lu S， Tu Y C， Lu H. Predictive condition-based maintenance for continuously deteriorating systems［J］.Quality and Reliability Engineering International，2007，23(1):71－81.

［100］Kaiser K A， Gebraeel N Z. Predictive maintenance management using sensor-based degradation models［J］.IEEE Transactions on Systems，Man，and Cybernetics-Part A:Systems and Humans，2009，39(4):840 －849.

［101］Wu S J，Gebraeel N Z，Lawley M A，et al.A neural network integrated decision support system for conditionbased optimal predictive maintenance policy［J］.IEEE Transactions on Systems，Man，and Cybernetics-Part A:Systems and Humans，2007，37(2):226 －236.

［102］Kharoufeh J P，Cox S M.Stochastic models for degradationbased reliability ［J］. IIE Transactions， 2005， 37:533－542.

［103］Kharoufeh J P，Solo C J，Ulukus M Y.Semi-Markov models for degradation-based reliability ［J］.IIE Transactions，2010，42:599－612.