楔形阻尼层复合梁式吸振器设计及实验研究
肖和业,盛美萍,刘儒林
(西北工业大学 航海学院,西安 710072)
梁式动力吸振结构模态丰富,可以等效为多个动力吸振器,能够对弹性薄板结构振动进行宽带控制,以降低飞机、汽车壁板振动对零件、仪表的危害[1-4]。国内外已有很多学者开展这方面的研究,其中,杨智春[5]提出了用梁式动力吸振器来抑制夹层壁板颤振,分析了带吸振器夹层壁板的振动特性、频率响应特性和颤振特性。Eiichi Nishida[6]设计了一种梁式宽带动力吸振器用于结构的振动与噪声控制,并通过实验验证了吸振器宽带吸振特性。上述梁式吸振器都由梁及其末端质量块组成,梁的作用相当于经典吸振器中的弹簧,其本身不作为一种连续吸振结构,如果将梁作为一种新的吸振结构对弹性薄板进行吸振,梁式动力吸振器结构将更为简单,工程应用更为方便。对于梁本身作为吸振结构用于振动控制,宛敏红[7]等开展了梁式动力吸振器用于抑制薄板振动的研究,但该种结构不含阻尼结构,对吸收能量耗散能力较差,进而影响吸振效果。本文在该种结构上复合变截面阻尼层,作为一种新型吸振结构,用于控制薄板结构的振动。该吸振结构相比传统的集中质量吸振器,具有吸振效果好、可控制频带宽、结构简单、安装方便等优势,但阻尼层性能不确定给设计带来不便。
整个新型吸振结构属于复合阻尼结构,对复合阻尼结构振动分析,有限元方法不仅成熟,而且运用广泛[8,9],因此,本文运用有限元方法设计吸振器的参数,研究该新型结构的吸振效果,得到一致性规律,并通过实验进行了验证,使得变阻尼层复合梁式动力吸振器在实际工程中应用成为现实。
1 复合梁吸振有限元模型
本文采用的变阻尼层复合梁结构如图1所示。吸振结构采用在钢质基底梁上粘贴变截面阻尼层的方式获得。图中h1为复合梁阻尼层初始高度,h2为阻尼层末端的高度,H为基底层厚度,阻尼层的厚度随着长度呈线性变化。在L型连接处中心开小孔用以与主振系统进行平行安装。
本文的控制对象为长 0.5 m、宽 0.5 m、厚 0.002 m、四边简支的薄板,在板(0.1 m,0.2 m)处施加一个激励力F,将复合梁与板用螺栓连接,运用ANSYS有限元软件建立梁板振动耦合有限元模型,如图2所示。在建模过程中,假设梁板连接面完全接触,结合处合并为一体,梁与板可简化为通过短杆进行连接,在有限元模型中,变截面阻尼梁通过壳单元shell99来模拟,板,短杆运用shell63单元进行描述。
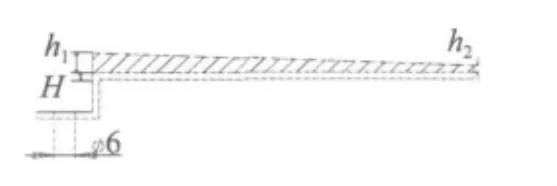
图1 复合梁反L型连接结构示意图Fig.1 L-shape connection of composite beam
吸振器对主振系统不同区域的吸振效果不同,为了衡量吸振器对整个被控制结构平均的吸振效果,需要对安装吸振器前后结构振动的平均振动能量进行计算,在本文分析模型中,板结构的平均振动能量为:
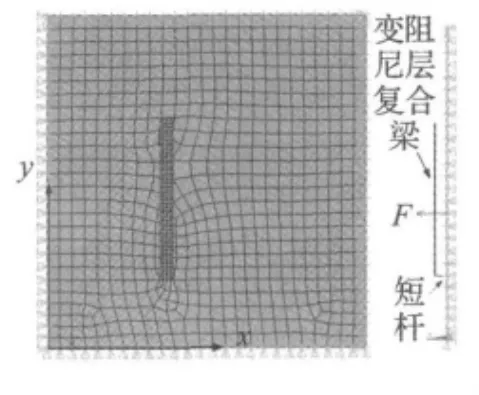
图2 梁板耦合有限元模型Fig.2 Finite element model of beam and plate coupling system

其中m为板的质量,n为板上节点的个数,Vi为板第i个节点的振动速度。
通过对安装吸振器前后的模型分析计算,可得板结构平均振动能量大小,吸振器的吸振量为[10]

E前为不安装吸振器板平均振动能量;E后为安装吸振器板平均振动能量。
2 复合梁参数设计及吸振效果分析
按照吸振理论,当吸振器固有频率与主振系需要控制的模态频率相等时,吸振器吸振效果才最好。因此,本文根据被控制结构模态,设计复合梁的参数,使其固有频率与板的模态相对应,确保复合梁的吸振效果。首先分析获得板前四阶模态频率如表1所示。

表1 板的固有频率Tab.1 Model frequencies of plate
在复合梁所有结构参数中,梁长度的改变对其模态影响最大[11],因此可通过改变梁长度来调节复合梁的固有频率,使之与主振系统需控制模态频率相对应。设定阻尼层材料密度为 ρ2=1600kg/m3,杨氏模量 E2=4.2 ×108N/m2,初始厚度 h1=0.004 m,末端厚度 h2=0.002 m;基底梁为钢质,密度 ρ1=7800kg/m3,杨氏模量 E1=2.1 ×1011N/m2,厚度 H=0.001 m。通过ANSYS分析获得复合梁前三阶模态频率随其长度变化的曲线如图3所示。依据板前四阶模态频率结合图3可以反推出梁的长度,具体数值如表2所示。

图3 ANSYS计算的梁固有频率随长度变化曲线Fig.3 Model frequencies of beam various with its length

表2 不同复合梁的固有频率及其吸振量Tab.2 Model frequencies and absorption of different beam
将这些长度的梁与板相连,在ANSYS中建模进行分析,在后处理模块中,通过式(1)、式(2)可计算获得梁不同阶模态对板前四阶模态频率的吸振效果,如表2所示。复合梁用不同阶模态对板同一阶模态进行吸振,复合梁用于吸振的模态阶数越高,吸振效果越差。不同长度的复合梁使用同一阶模态控制板的不同模态频率的振动,随着板模态阶数增加,复合梁吸振量上升,结合表2中复合梁长度的数值可知,吸振量越高,梁的长度越短。这是由于梁长度越短,模态个数越少,等效吸振器个数越少,每个等效吸振器质量越大,吸振效果越好。随着梁的长度增加,梁模态个数在分析频率内增加,等效吸振器的个数增多,吸振频带变宽,但等效吸振器的质量下降,导致吸振效果下降。为了说明该问题,分别分析了长度为0.335 m和0.2 m的复合梁,在板上(0.07 m,0.17 m)安装的吸振效果,结果如表3所示。

表3 不同梁长度的吸振量Tab.3 Absorption of beam with different length
由于加工中存在偏差,加工成型的复合梁的长度与设计的结果有一定的偏差,这使得梁模态频率与理论分析不同,影响其吸振效果。为了分析梁长度的加工误差对吸振效果的影响,确定具有吸振效果梁长度的可变范围,以固有频率与主振系统模态频率相同的梁的长度为中心,增加或者减少梁长度,改变其固有频率,研究吸振频率扰动对吸振效果的影响,结果如图4所示。随着复合梁用于吸振的模态阶数增加,复合梁具有吸振效果的固有频率范围缩小,吸振效果变差。设定安装吸振器板平均振动能量下降5 dB以上,吸振器才具有吸振效果,通过图4并结合梁长度与固有频率之间的关系,可以获得具有吸振效果复合梁长度的可变范围,具体数值如表4所示。随着复合梁用于吸振的模态阶数降低,具有吸振效果的梁长度可变范围增大。

图4 梁模态频率变化对板各阶模态吸振效果影响Fig.4 Absorption of different mode of plate various with beam model frequencies

表4 具有吸振效果的梁长度可变范围Tab.4 The length variable scale of beam used to control vibration of plate

图5 吸振器安装位置变化对板各阶模态频率吸振量的影响Fig 5 Absorption of different mode of plate with different beam location
由于不同频率下在板上不同位置点安装吸振器,吸振效果不同,为了获得安装吸振器位置对吸振性能影响的一般规律,分析在板不同位置安装复合梁对板前四阶模态频率吸振效果,结果如图5所示,图中圆点代表激励位置。板第一阶模态频率吸振效果最好的区域在板中心靠激励点附近。第二阶模态频率吸振效果最好的区域分为两片且中心对称,其中一片在激励点附近。第三阶模态频率吸振效果最好的区域也中心对称,不过分为4片区域,其中一片区域也在激励点附近。第四阶模态频率吸振效果最好的区域也为两片且轴对称,其中一片分布就在激励点附近。总结以上结果可得,虽然在不同模态频率下,吸振效果较好的区域分布不同,但在激振点附近区域,其吸振效果都比较显著。
3 实验方案
为了验证仿真分析获得的结论,对复合梁式动力吸振器的吸振效果进行实验测量。测试中的主振系统尺寸与仿真分析中相同,变截面复合梁的参数如表5所示。将板均匀划分25个网格,在每个网格内任意取点拾振,获得网格内振动响应,根据式(1),式(2)可获得吸振器吸振效果。
测试中激励点位置与仿真分析中激励点位置相同,坐标为J(0.1 m,0.2 m)。为了验证图5中吸振器安装位置不同对其吸振效果影响的规律,首先在激励点附近选择一安装点 x1(0.07 m,0.17 m),依据图5中各阶模态吸振效果差异较大的区域进一步选择x2(0.20 m,0.35 m),x3(0.25 m,0.25 m),x4(0.35 m,0.17 m),x5(0.4 m,0.4 m)作为安装点,其具体分布如图6所示,图中五个△分别表示吸振器的五个不同安装位置,○表示激振位置。

表5 变阻尼层复合梁参数列表Tab.5 Parameters of composite beam
实验时将试件与板通过螺栓进行连接,用信号发生器产生20 Hz~500 Hz白噪声,通过功率放大器,输入到激振器,激励板振动。用加速度传感器采集信号,通过电荷放大器,输入到采集分析仪,对数据进行分析,整个测试系统结构如图7所示。

图6 板上激振点、拾振区域、吸振器安装点分布示意图Fig 6 Distribution of driving point,dynamic vibration absorber location and Accelerometer position in plate

图7 测试系统结构图Fig.7 Experiment measurement system

图8 安装位置不同对吸振效果的影响Fig.8 Absorption of the plate
4 实验结果
实验中首先分析吸振效果最好的安装位置,在x1~x5位置分别安装试件1、2,对板的第二、三阶模态进行吸振,效果如图8所示。对板第二阶模态进行吸振,只有x1位置处的吸振效果好,x2、x3位置吸振效果较最差。对板第三阶模态进行吸振,x3位置吸振效果最差,x2、x4位置、x1、x5位置吸振效果接近。结合图 5、图 6 可知,对于板不同模态频率下,吸振效果较好的区域在激振点附近区域,实验与仿真分析结论一致。

图9 安装试件1前后板的平均振动能量Fig 9 The average energy of plate fitted with and without sample 1
为了分析梁长度对复合梁吸振性能影响,实验中在x1位置分别安装试件1、2,板上平均振动能量与不安装吸振器的情况对比如图9、图10所示。安装试件1对板第二、七阶模态具有良好的吸振效果;安装试件2对板第一、二、三阶模态都具有好的吸振效果,吸振量具体数值如表6所示。随着梁的长度增加,吸振频带变宽,吸振效果下降。结合表3的结果可知,复合梁的实际吸振效果小于理论计算值,这是由于梁板通过螺栓进行连接,连接面未完全接触,传递到梁的振动能量较理论计算数值小,吸振量降低。实验中0.2 m的梁控制板的第二、七阶模态,而数值仿真计算结果为吸收板的第二、五阶模态的振动,这是由于实际加工中,阻尼层与基底层粘贴过程中粘贴剂形成粘贴层,影响梁模态频率,导致吸振频率偏移。结合表2、表6可知,0.2 m,0.33 m的复合梁分别运用其第二、第三阶模态对板第二阶模态进行吸振,随着梁用于吸振模态阶数增加,对板的吸振效果下降。

表6 实验测得不同长度复合梁的吸振效果Tab.6 Experimental absorption of different length beam
5 结论
本文以简支板为控制对象,运用有限元方法设计了复合梁长度,研究了复合梁不同阶模态、不同长度及不同安装位置对板吸振效果影响,并最后通过实验验证了仿真获得规律,得到以下结论:
(1)复合梁用于吸振的模态阶数越高,对板的吸振效果越差,运用复合梁同一阶模态控制板的不同模态频率振动,随着板模态阶数增加,吸振量增大。
(2)复合梁用于吸振的模态阶数越低,梁具有吸振效果的长度可变范围越大。
(3)随着长度增加,用于吸振模态个数增加,复合梁式动力吸振器吸振频带变宽,但每个吸振频率的吸振量下降。
(4)对于板不同模态,吸振效果显著的区域分布不同,但是在激振点附近区域,其吸振效果在不同频率下都比较显著。
[1]王彦琴,盛美萍,孙进才.变截面梁式动力吸振器的宽带吸振机理[J].振动工程学报,2004,17(4):473-476.
[2]杨 飞,杨智春,王 巍.吸振夹层壁板颤振抑制的吸振器频率设计[J].振动与冲击,2009,28(7):65 -68.
[3]De Espindola J,Bavastri C A,Lopes E M O.On the passive control of vibrations with viscoelastic dynamic absorbers of ordinary and pendulum types[J].Journal of the Franklin Institute,2010 ,347:102 -115.
[4]Jang S J,Choi Y J.Geometrical design method of multidegree-of-freedom dynamic vibration absorbers[J].Journal of Sound and Vibration,2007 ,303:343 -356.
[5]杨智春,杨 飞,张玲凌.动力吸振器用于夹层壁板颤振抑制的研究[J].振动与冲击,2009,28(2):25-71.
[6]Eiichi Nishida G H.Koopmann.A method for designing and fabricating broadband vibration absorbers for structural noise control[J].Journal of Vibration and Acoustics,ASME,2007,129:397-405.
[7]宛敏红,王敏庆,行晓亮,等.梁式动力吸振器用于抑制薄板振动的研究[J].噪声与振动控制,2007,27(1):27-30.
[8]郭亚娟,李惠清,孟 光,等.粘弹性自由层阻尼管的有限元建模与试验研究[J].振动与冲击,2008,27(5):99-102.
[9]刘利军,王贡献,张志谊,等.绕定轴转动的主动约束层阻尼板的振动控制研究[J].振动与冲击,2008,27(8):138-143.
[10]王彦琴.新型宽带动力吸振器的研究[D].西安:西北工业大学,2003.
[11]肖和业,盛美萍,陶红丹.变阻尼层复合梁动力特性的优化分析[J].振动、测试与诊断,2010,30(1):43 -46.

