基于二维DCT的电能质量监测数据压缩方法

胡志坤，何志敏, 安 庆, 孙克辉, 丁家峰

(1. 中南大学 物理科学与技术学院，湖南 长沙，410083；2. 河南省电力公司周口供电公司，河南 周口，466001)

随着电能质量(Power quality, PQ)不断降低以及网络技术的发展，电能质量监测网得到广泛应用，建立了大量的电能质量管理中心。为了有效地分析电能质量问题，电能质量监测数据需要保证高实时性，即需要有高采样频率。电能质量监测网记录了大量的数据，监测点与监测中心间的通讯量很大，无论是传给监控中心还是就地存储都非常困难，必须对电能质量监测数据进行压缩。由于录波器的录波机制，电能质量监测数据具有周期性，可利用其周期性得到更好的压缩性能。Santoso等[1-2]提出了小波系数阈值压缩方法，将数据转化为小波系数表示，利用阈值法选取小波系数中的重要成分，实现数据压缩。Panda等[3]引入改进小波(Slantlet)的阈值处理方法来进行数据压缩。Hamid等[4-7]采用小波包与最小描述长度判据相结合的方法进行数据压缩。Gerek等[8-12]将一维电能质量检测数据表示成二维形式，并对其进行数据压缩，因其具有形象性、相关度高等优点，获得了较好的压缩效果。但小波变换的计算需要消耗大量内存，计算复杂、实现实时性成本高[13]。Ahmed等[14]提出了离散余弦变换(DCT)，其变换矩阵的基向量近似于 Toeplitz 矩阵的特征向量，被认为是性能接近于K-L变换的准最佳变换，它具有很强的“能量集中”特性，大多数自然信号(包括声音和图像)的能量都集中在离散余弦变换后的低频部分。为了更形象表达电能质量，借助电能质量的周期性和DCT算法的简便性，本文作者研究一种基于二维分块的DCT电能质量监测数据压缩方法。

1 数据压缩与重构

设某个电能质量监测数据的采样时间序列为a ( i)，1≤i≤m×n，每信号周期采样n点，共有m个周期。将每周期的n个数据作为二维数据的1行，将m个周期的电力信号按照时间的顺序排成列，即构成了1个m×n二维数据矩阵。

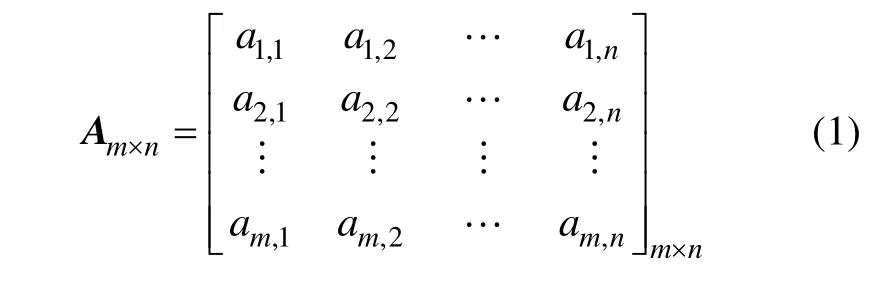
设m和n是8的倍数，先对其进行分块，设分块大小为8×8，得到数据矩阵如下：

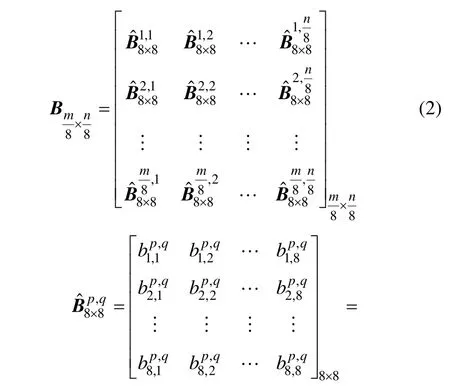
式(9)的8×8的分块系数矩阵能量分布差别很大，变换系数的能量多半集中于左上角，并且具有向右下角逐渐减少的特点。将各分块系数矩阵中位置相同的DCT系数排列在一起，即将所有个中位置相同的元素组成1个矩阵，元素 cp,q放在重排后位置为(i,j)的子阵中，元素在子阵中的位置为(p, q)。系数矩阵经过重排后由 8×8个的二维矩阵组成，即：

定义D8×8为重排矩阵，为分块重排矩阵。重排流程如图1所示。

每个分块重排矩阵中，数据都处在一个数量级且方差很小。因此，可以采用平均能量阈值法选取对原始数据贡献大的分块重排矩阵。平均能量阈值法采用如下步骤。

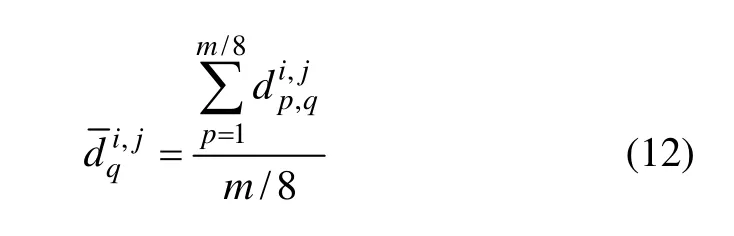
步骤2 对行向量求标准差：

式中：pi,j表示的是向量(或者矩阵Dˆi,j)的平均能量。由重排矩阵D8×8得到1个8×8的能量矩阵：

步骤3 设定1个能量阈值σ，当 pi,j大于该阈值σ时，将对应的分块重排矩阵设置为保留，量化矩阵对应的位置为 1；当 pi,j小于阈值σ时，则将对应分块重排矩阵丢弃，量化矩阵对应的位置为 0。量化矩阵如下：

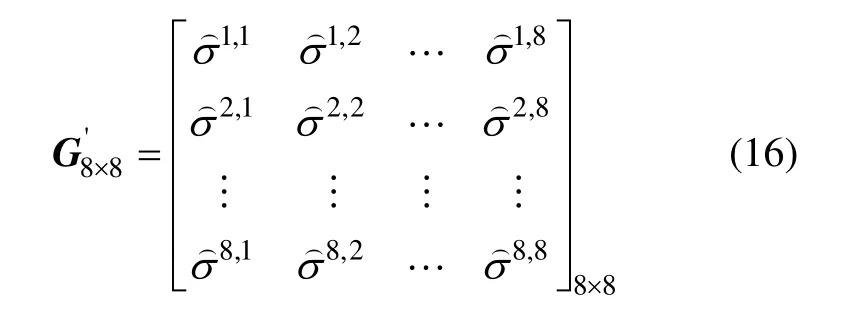
图1 系数排列过程Fig.1 Processes of coefficients swap

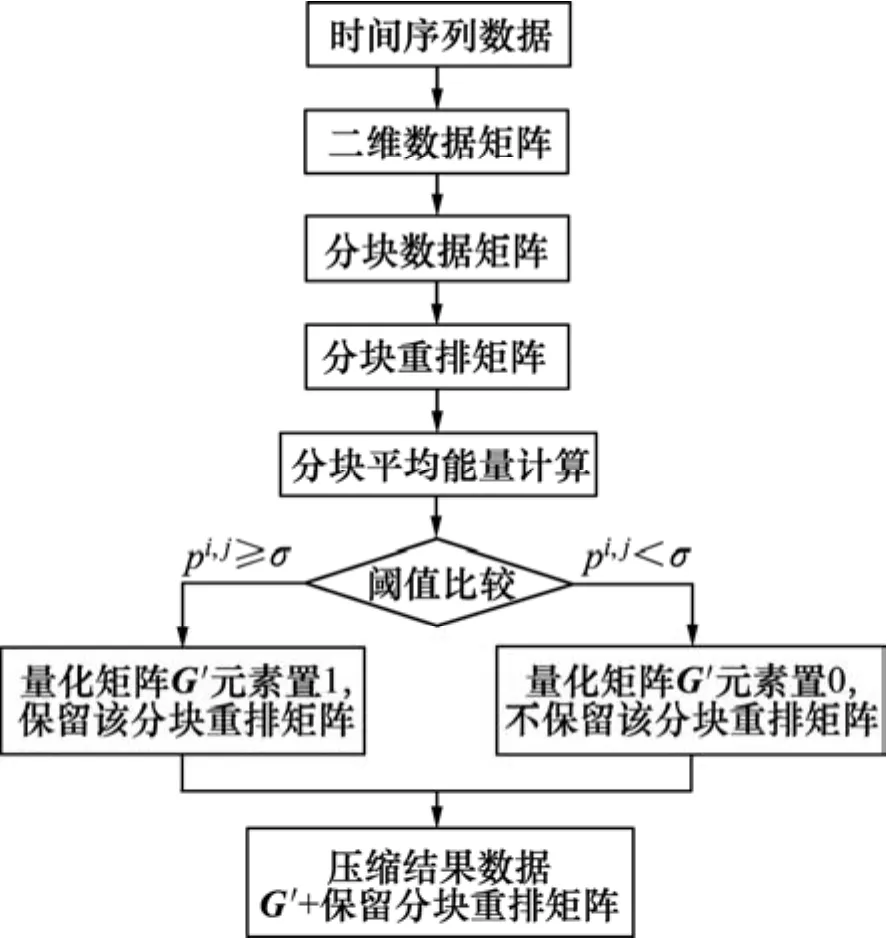
图2 数据压缩流程Fig.2 Process of data compression

经二维逆DCT变换后，即可得到 nm× 的重构信号矩阵，再按照二维数据一维顺序化的方法即得到重构信号。数据重构流程如图3所示。

图3 数据重构流程Fig.3 Process of data reconstruction

2 数值仿真

压缩性能的主要评价指标包括压缩比、信噪比和均方误差。

(1) 压缩比为：

式中：NC表示压缩后数据长度，设 G '中 1的元素个数为 r，则N =+64；N为原始信号的数C据长度。压缩比越大、性能越好，压缩比为0时表示没有压缩。

(2) 信噪比为：

(3) 均方误差eMSE为：

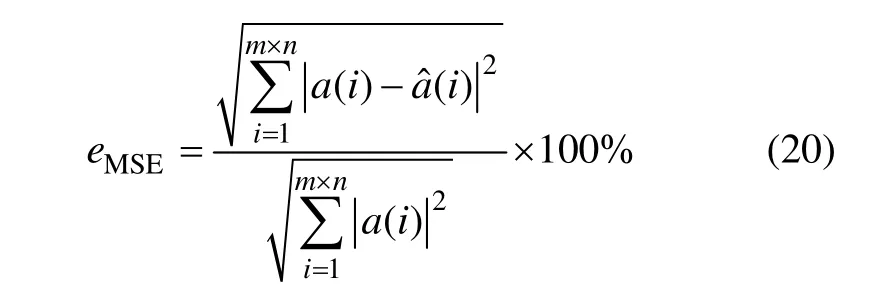
均方误差用于评价压缩产生误差的相对大小。以电力系统的电压扰动信号作为试验对象，扰动类型有电压凹陷、电压凸起、电压闪变、谐波畸变、电压中断等。仿真试验中，使用 MATLAB生成每周期 512点的采样信号，总共512个电力周期。采样信号构成512×512的矩阵，其二维表示见图4。

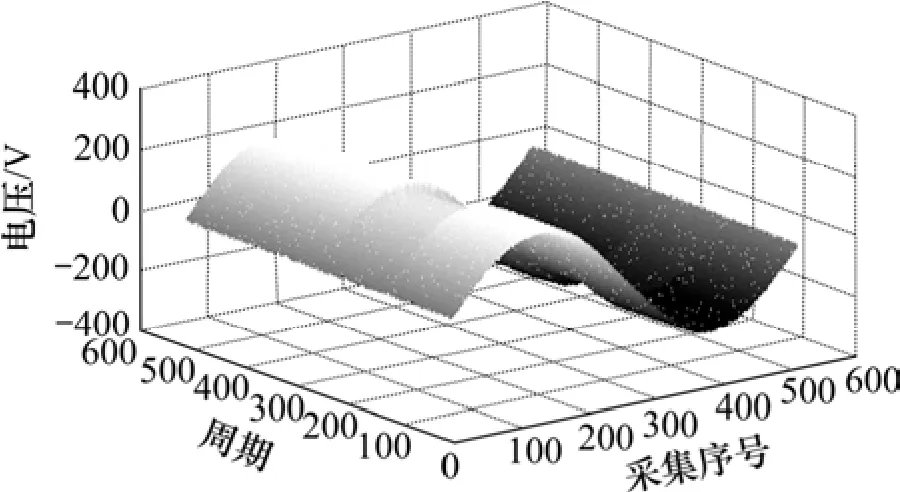
图4 一维时序数据的二维表示Fig.4 Two-dimension expression of one-dimension data

电压凹陷80%加上20 dB高斯噪声作为故障信号进行仿真，电压凹陷信号见图5，压缩重构信号见图6。

图7和图8所示分别为电压闪变的原始信号和压缩重构的波形图，该信号是5 Hz的闪变，信号表达式为：

在该信号上加20 dB高斯噪声。从图5~8可以看出：重构信号中的高斯噪声明显减少，但是，信号的其他细节基本上没有改变。

图5 电压凹陷原始信号Fig.5 Original signal of voltage sag

图6 电压凹陷重构信号Fig.6 Reconstructed signal of voltage sag

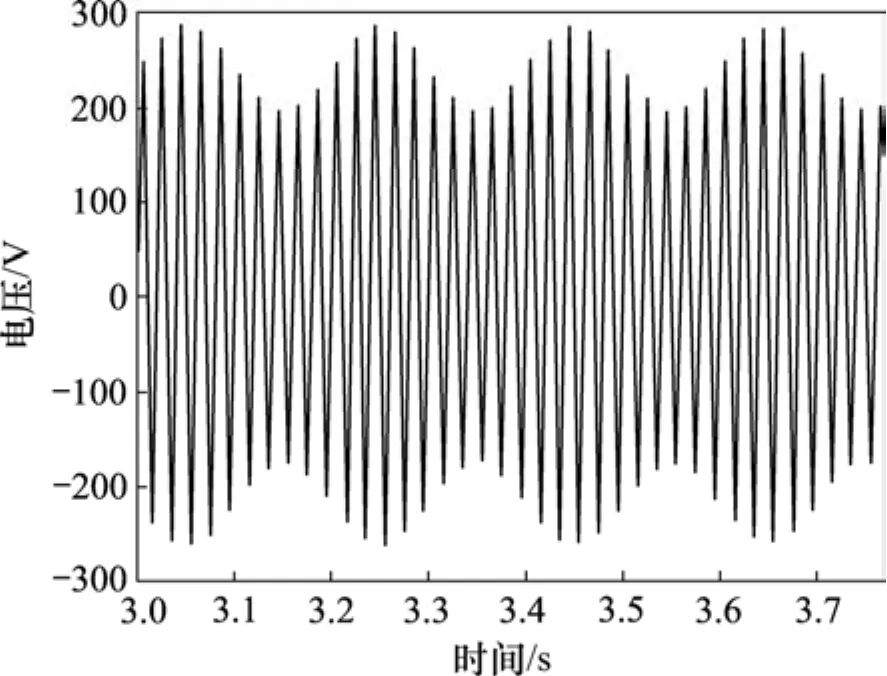
图7 闪变原始信号Fig.7 Original flicker signal

由压缩性能评价指标公式，得到的电压凹陷数据压缩评价数据见表1。

图8 闪变重构信号Fig.8 Reconstructed flicker signal

表1 电压凹陷数据的压缩结果Table1 Compression results of voltage sag data

由表1可知：当阈值σ较小时，压缩比会变小甚至为0；当σ较大时，压缩比增大，但会产生较大的均方误差。根据表1可知：在阈值σ=0.901 5时，压缩比CR和信噪比SNR较高，均方误差eMSE较小，σ取得一个比较合适的值。

设定σ=0.901 5，对电压凸起、电压闪变、谐波畸变、电压中断等故障电压信号作仿真实验，得出评价数据如表2所示。

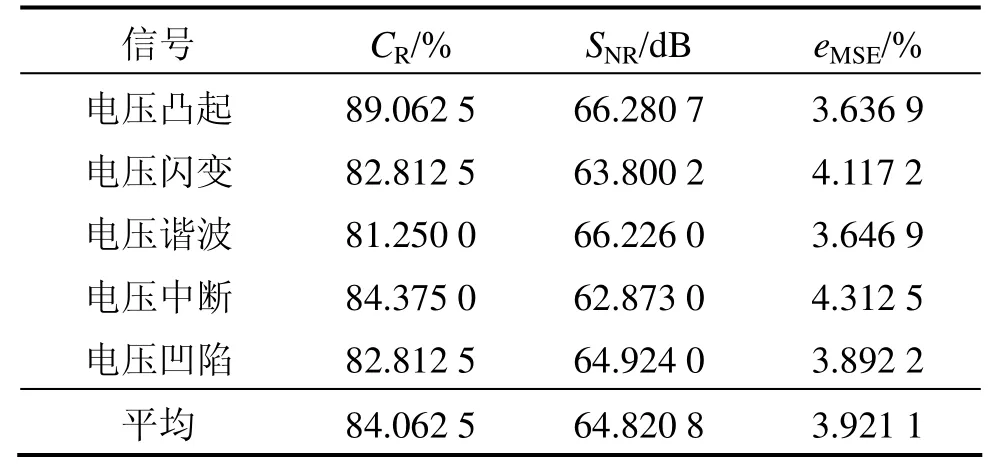
表2 σ=0.901 5时的压缩评价数据Table2 Compression results when σ=0.901 5

将本文提出的方法与文献[16]中提到的压缩方法进行比较，如表3所示。

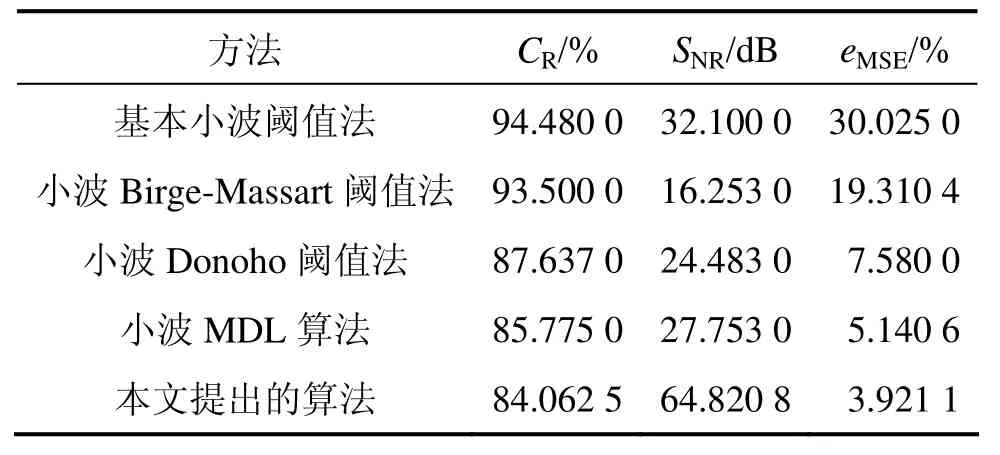
表3 多种压缩方法的比较Table3 Comparison of several methods

由表3可知：算法1和算法2虽然能够达到很高的压缩比，但是，均方误差太大。采用小波 Donoho阈值法、小波 MDL算法和本文中提出的方法能够达到比较大的压缩比，同时均方误差也比较小，表明这些方法有很强的实用性，但本文提出的方法其信噪比较高，均方误差较小。

3 结论

(1) 将一维电能质量检测数据转化为二维数据格式。利用二维电能质量数据的相关性、局部平稳性以及二维信号处理的灵活性实现数据压缩。

(2) 采用分块二维DCT算法，速度快。并根据二维DCT系数的分布特性，通过重新排列DCT系数为数据压缩提供必要条件。

(3) 设定平均能量阈值实现信号重要信息的筛选。

[1] Santoso S, Powers E J, Grady W M. Power quality disturbance data compression using wavelet transform methods[J]. IEEE Transactions on Power Delivery, 1997, 12(3): 1250-1257.

[2] Littler T B, Morrow D J. Wavelets for the analysis and compression of power system disturbances[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 358-364.

[3] Panda G, Dash P K, Pradhan A K, et al. Data compression of power quality events using the slantlet transform[J]. IEEE Transactions on Power Delivery, 2002, 17(2): 662-667.

[4] Hamid E Y, Wasaki Z I. Wavelet-based data compression of power system disturbances using the minimum description length criterion[J]. IEEE Transactions on Power Delivery, 2002,17(2): 460-466.

[5] Mehta K B, Russel B D. Data compression for digital data from power system disturbance: Requirements and technique evaluation[J]. IEEE Transactions on Power Delivery, 1989, 4(3):1683-1688.

[6] Hsieh C T, Huang S J, Huang C L. Data reduction of power quality disturbances—A wavelet transform approach[J]. Electric Power Systems Research, 1998, 47(2): 79-86.

[7] Ribeiro M V, Park H, Marcos J, et al. A novel MDL-based compression method for power quality applications[J]. IEEE Transaction on Power Delivery, 2007, 22(1): 27-36.

[8] Gerek O N, Ece D G. 2D analysis and compression of power quality event data[J]. IEEE Transactions on Power Delivery,2004, 19(2): 791-798.

[9] Ibrahim W R A, Morcos M M. Artificial intelligence and advanced mathematical tools for power quality applications: A survey[J]. IEEE Transactions on Power Delivery, 2002, 17(2):668-673.

[10] Gaouda A M, Salama M M A, Sultan M R, et al. Power quality detection and classification using wavelet-multiresolution signal decomposition[J]. IEEE Transactions on Power Delivery, 1999,14(4): 1469-1476.

[11] Ece D G, Gerek O N. Power quality event detection using joint 2D-wavelet subspaces[J]. IEEE Transactions on Instrumentation and Measurement, 2004, 53(4): 1040-1046.

[12] Gerek O N, Ece D G. Compression of power quality event data using 2D representation[J]. Electric Power Systems Research,2008, 78(6): 1047-1052.

[13] 高培生, 陈新建, 吴为麟, 等. 二维表示的电能质量故障数据压缩[J]. 浙江大学学报: 工学版, 2008, 42(4): 686-690.

GAO Pei-sheng, CHEN Xin-jian, WU Wei-lin, et al.Compression of 2D representation of power quality event data[J].Journal of Zhejiang University: Engineering Science, 2008,42(4): 686-690.

[14] Ahmed N, Natarajan T, Rao K R. Discrete cosine transform[J].IEEE Transactions on Computers, 1974, C-23(1): 90-93.

[15] Britanak V, Yip P C, Rao K Q. Discrete cosine and sine transforms: General properties, fast algorithms and integer approximations[M]. Boston: Academic Press, 2006: 119.

[16] 李鹏, 杨洪耕, 孔飘红. MDL判据在电能质量扰动信号数据压缩中的应用[J]. 电网技术, 2004, 28(18): 48-52.

LI Peng, YANG Hong-geng, KONG Piao-hong. Application of minimum description length criterion in data compression of power quality disturbance signal[J]. Power Systems Technology,2004, 28(18): 48-52.