基于层次性的交通网络资源优化配置方法

曾明华，李夏苗

(1. 华东交通大学 轨道交通学院，江西 南昌，330013；2. 中南大学 交通运输工程学院，湖南 长沙，410075)

基于层次性的交通网络资源优化配置方法

曾明华1，李夏苗2

(1. 华东交通大学 轨道交通学院，江西 南昌，330013；2. 中南大学 交通运输工程学院，湖南 长沙，410075)

利用交通网络层次性这一基本特征，研究随机交通配流算法与交通网络资源优化配置方法。在分析算法的设计基础上，定义层次因子，并提出利用复杂网络拓扑特征或交通关联度来确定交通网络的层次数目和层次因子，在Dial算法的基础上利用层次性设计层次随机交通分配算法(HSTAA)；通过算例验证与分析HSTAA算法，提出基于层次性的交通网络资源的优化配置方法。研究结果表明：由HSTAA算法得到的交通网络总阻抗在层次因子的某一合理取值范围内小于 Dial算法所得的总阻抗，且交通网络的总阻抗随较高层次路段层次的提高而减小，但交通网络的尾气排放总量却随较高层次路段层次的提高而增大，但它始终小于由Dial算法所得到的结果；将网络层次状况控制在合理范围内就能有效地调节和优化交通网络资源配置。

交通网络；优化配置；层次性；层次因子；Dial交通分配算法

由于有关综合交通运输网络结构、交通运输网络资源合理配置等体现可持续发展特征的综合交通运输网络研究相对滞后[1]，因此，开展交通网络资源优化配置的研究具有重要的理论价值和现实意义。国内外对交通运输网络结构研究很多，在研究方法和手段上，基本上采用分形分析方法[2]、耗散结构理论[3]、复杂网络理论[4]或数学规划等理论[5−7]。这些研究在交通网络规划中起重要作用，但可以认为这些对交通运输网络结构的研究绝大多数只是在具体理论与方法上存在差异。考虑到层次性是交通运输网络的几大系统特性之一，层次性的观点是现代系统论三大支柱观点之一，且以往关于层次性的研究成果较少[8−11]，在此，本文作者从交通网络本身的基本特征即层次性出发，研究交通网络资源的优化配置问题。其步骤为：首先，针对层次性定义层次因子；然后，在 Logit交通分配模型的典型代表即 Dial算法[12]的基础上设计基于层次性的层次随机交通分配算法；最后，在算法的实例检验与分析基础上提出交通网络资源优化配置的操作步骤与方法。

1 符号系统

假设研究对象是某区域的交通网络，该区域的交通小区划分情况及交通网络分布状况如图1所示。其中：虚线表示交通小区的边界；实线表示处于较高层次的路段；虚线表示处于较低层次的路段；圈内数字表示交通网络中的节点编号，它也对应于小区编号(1个小区有多个交通网络节点的情况不影响本研究结论的一般性)。

图1 某区域交通分区及其交通网络布局图Fig.1 A schematic layout of traffic zones in a region and its transport network

将交通网络系统表示为C=(V,A)(其中：V为节点集合{…,i, …}；A为路段的集合{…,a=(i,j), …}，(i,j)V×V)；交叉口排队时间为da，a∈Aj(其中，Aj为进入信号控制路口j的所有路段的集合，且满足A=UjAj)；W ={… ,w,…} 为所有起讫点(OD对)的集合(其中，w代表 OD对o−d)；Rw为OD对w之间的路径集合{…,r, …}；I(i)与O(i)分别表示进入与离开节 点i的 邻 接 点 集 合 ， I(i) ={(l,i) ∈A}，O(i) = {(i,j) ∈A}；qw为OD对w∈W之间的交通流量；H= {1,2,… ,ħ,…} 代表区域中交通模式的层次集合；为OD对w间选择路径r∈Rw上层次ħ∈H的阻抗；为OD对w间选择路径r上的阻抗；ta与va分别表示路段 a ∈A= {(i,j)}的阻抗函数与流量；uw为从OD对w的起始点o到终讫点d间的最小阻抗；oi为OD对o−d的起始节点o到所有其他节点i∈V的最小阻抗；为OD对w之间的路径r∈Rw的选择概率；Δ =()表示路段−路径关联矩阵，当边a在路径r时，为1，否则为0；La表示路段a的路段似然值；Wa表示路段a的权重；交通网络的总阻抗与尾气排放总量分别表示为TI与Ee。

2 基于层次性的随机交通分配算法

Logit加载是随机交通分配的 2种经典分配技术之一，简洁、流行。Logit加载的常用算法有Dial[12]、Bell[13]和 Leurent[14]等提出的方法，其中，最著名的Logit加载方法为Dial[12]提出的Dial算法。

Dial算法与其他 Logit加载模型一样，考虑了 1个参数θ。该参数θ是影响路径选择的重要因素，它反映了理解出行费用的偏差和出行者对出行条件的了解程度[15−16]，体现了分配模型的全部随机特征[13]。

本节基于层次性设计的HSTAA算法，有区别地处理不同层次路段。该算法为Logit交通分配算法。

2.1 算法基础及原理分析

2.1.1 算法的设计基础

层次的思想在交通网络规划中常常用到。美国在1950年提出了“市区道路网规划中根据高速道路、干线道路、局部道路的不同功能赋予明确的特性分工，按一定层次构成网络”的思路[17]。我国在交通运输网络规划如城市公交网络规划中也常采用这种方法[18−19]。但关于交通网络分层规划的实践，基本上建立在经验和感性认识之上，缺乏一定的基础理论支持。国内外在交通网络分层规划的理论研究方面[18−20]较缺乏，滞后于规划实践。

Dial算法的技术要点之一是采用最短路径搜索技术确定被选择的路径，最常用的最短路搜索算法是Dijkstra算法。根据人类思维特点及消费者行为心理学，出行者一般倾向于选择路面质量好、道路宽、最高限速高、技术等级高、交通信息服务全面和准确等路段出行，从而使出行者的效率、安全和舒适度得到更大保障。也就是说，出行者往往使自己的最优路径尽可能地选择在较高层次完成。然而，这在交通网络平衡配流算法通常所采用的最短路径搜索算法寻找到的最短路径中并不能体现，这些最短路径中往往包含一些狭窄的小巷或者由一些等级较低的路段构成，在这些低等级路段上行驶有更大概率碰到交通突发事件，且如果这些路段分配的流量过大，会妨碍社区邻里的生活；这样的低等级路段越多，所需切换的次数越多，所需的切换时间和心理成本越大，可能造成路段交叉口和层次切换处交通拥堵；因此，要选择包含尽量多快速通道和交通干道等层次较高的路径，尽可能减少在不同层次的路段间切换次数。

其次，Dial算法的1个突出特点是：考虑了实际网络中有许多路径明显不会被出行者选择，这在Dial算法中通过初始阶段的有效路径识别来完成，但是，这只是体现在不同路径的阻抗上，并不区别道路间显著存在的层次性。这种考虑是不全面的，也不尽合理。

2.1.2 基本原理

利用交通模式层次因子按下式计算OD对w间选择路径r上的阻抗：

Dial算法的1个典型特征是：在前向过程中，给所有路段分配1个权重，该权重为带参数的指数函数所表示的路段似然值。因此， ∀(i,j)∈A，定义路段似然值La如下：

其中：oi表示从起始点o到节点i的最小阻抗。由路段似然定义，路段所处层次越高，其路段似然值越大，该路段在交通均衡分配过程中被选择的概率越大。

2.1.3 评价准则

考虑交通网络总阻抗和尾气排放总量2个重要指标，分析层次性对交通网络资源优化配置的影响。

交通网络总阻抗为：

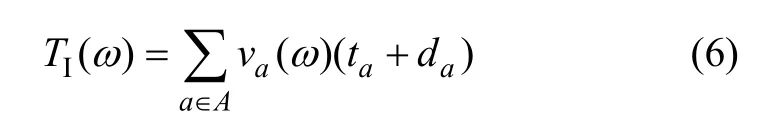
交通网络尾气排放总量为：

其中：hd为交叉口排放因子；为路段排放因子[21]，TI()ω与Ee()ω的定义域都为

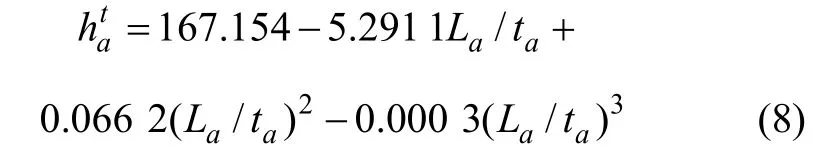
2.1.4 网络层次数目及层次因子的确定

分别基于复杂网络拓扑特征和交通关联度给出 2种算法，可根据实际情况选择。

(1) 利用复杂网络拓扑特征确定。复杂网络中节点(对应于图1中1条道路)的介数中心性BC(i)：

其中：nst与nst(i)分别为以s和t为始点和终点的全部最短路径数与这些最短路径中过i的条数。

① 大致估计。在一定的城市空间结构和产业结构下，2个交通小区间的交通关联度取决于它们之间的经济关系、空间联系难易程度、交通小区的人口规模和土地利用平衡程度。最初取()=1，然后按下述方法调整：若交通小区之间的三次产业互补明显，具有一定分工合作，则交通关联度取较大值；交通小区内部的土地利用均衡状况 (只考虑居住、商业、工业 3个主要城市功能之间的均衡状况)研究对交通关联度的影响。

(i) 上学出行对交通关联度的影响通常可忽略不计。

(ii) 商业和工业用地状况是产生上班和购物出行的主要因素。若2个交通小区都能为内部居民提供足够的就业岗位和购物场所，则对交通关联度的影响也可忽略。

确定交通关联度后，按照与方法(1)中相同的处理方式得到层次数目与各层次因子。

一旦确定了某条道路的层次因子，则该道路上的路段的层次因子自然也被确定，并与这条道路的层次因子相等。

2.2 层次随机交通分配算法(HSTAA)

对网络中的所有OD起始点均执行以下步骤，并累计路段流量。

步骤1：预处理。

(1) ∀i∈V，计算从起始点o到i的最短路径长度oi；

(2) ∀(i,j)∈A，按式(5)计算路段似然值。

步骤2：向前计算路段权重。

对路段似然值为0的路段首先确定其路段权重为0。从起始点o开始，按oi的升序依次考虑每个节点i，即对于节点i，按下式计算权重Wij：

步骤3：向后分配路段流量。

从具有最大oj的节点j开始反向计算，按oj的降序依次处理每个节点j，即， ∀i∈I(j)，按式(12)给路段(i,j)分配流量：

式中：qoj为从起始点o到节点j(可以是终点d)的交通量；若j不是某个OD对的终点，则取qoj=0；当O(j)为空集(如O(d))时，vjm=0。

可以证明：HSTAA的过程能为OD对间的所有有效路径产生1个服从Logit函数安排的流量分配。

3 算法检验与分析

交通网络取自文献[12](如图2 所示)，与文献[12]中网络的唯一的区别在于这里考虑交叉口排队时间。图2中，网络共9个节点、12条路段。路段的测定阻抗标在相应路段旁，如t12=2；设da=0.08， ∀ a ∈Aj，并假设L45=L56=0.9，其他路段长度为 1.2；设节点 1和9分别是唯一OD对的起始点和终讫点，OD交通量为qod=1 000。

图2中路段(4, 5)和(5, 6)处于第1层次ħ1(较高层次)，其他所有路段均为第 2层次ħ2(较低层次)，则相应的层次因子为,∈H。

按照HSTAA算法进行编程计算(取θ=1)，分配得到各路段流量。

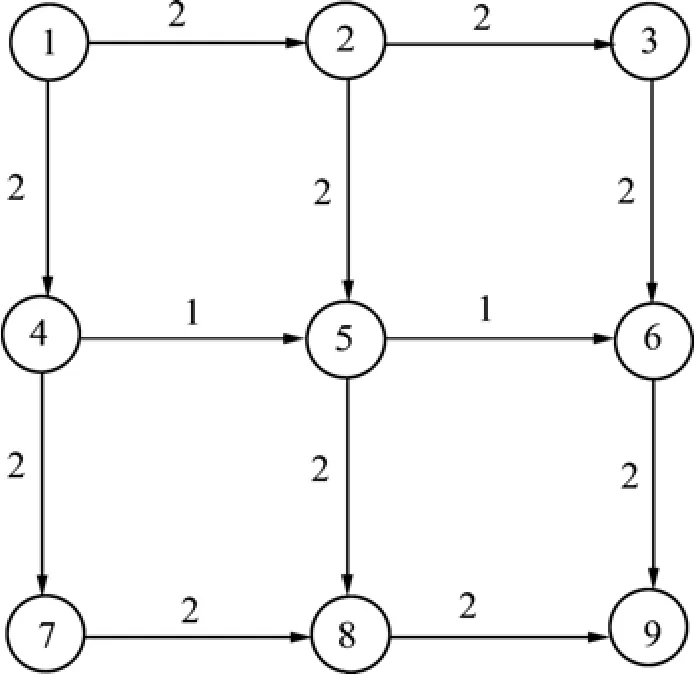
图2 实例网络Fig.2 Example network

3.1 用网络总阻抗分析层次性对资源配置的影响

由HSTAA算法分配得到的路段流量、路段阻抗及式(6)，得到交通网络的总阻抗：

图3 网络总阻抗Fig.3 Total impedance of traffic network

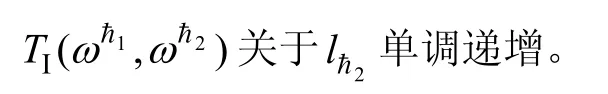
性质1与交通规划中从满足主要流向交通需求出发来建设交通干道以便实现用最少投资得到最大效益的实践是相吻合的。

3.2 层次因子对尾气排放总量的影响分析

取交叉口排放因子为hd=0.18 g/(辆·s)[21]。假设 1个单位长度、时间、流量分别为10 km，10 min和10辆车。根据式(7)～(8)，将各参数及由 HSTAA 算法得到的路段流量代入，经整理简化，即可得到尾气排放总量

性质2 说明：不能为了大幅度降低网络总阻抗而一味地提高较高层次路段的层次因子或降低较低层次路段的层次因子，否则，会导致交通网络尾气排放总量上升，当然，它始终小于Dial算法所得的结果。

4 交通网络资源优化配置方法

根据上述论述与分析，提出以下实际中交通网络资源优化配置的方法。

步骤1：利用第2.1.3节中的方法确定所研究交通网络的层次数目；

步骤 2：根据层次数目利用第 2.2节中设计的HSTAA算法分配路段流量；

步骤 3：利用评价准则分析层次因子对网络资源分配的影响，确定能使网络结构得以优化的ωħ(ħ∈H)的取值范围；

步骤4：对按第2.1.3节中方法得到的层次因子lħ(ħ∈H)进行微调，以确定符合实际的层次因子的调整值；

步骤5：将层次因子的调整值代回步骤2 得到路段流量表达式，计算最终路段流量，确定交通网络资源的优化配置方案。

5 结论

(1) 所设计的HSTAA算法与经典Dial算法相比有显著的区别：首先，HSTAA算法是基于层次特征的；其次，HSTAA算法比Dial算法在更大合理范围内调节流量加载，有效地优化交通网络结构，以便使得网络总阻抗和尾气排放总量皆小于Dial算法所产生的结果；因此，HSTAA算法比Dial算法在找到更优网络结构方面更具有灵活性。

(2) 采用所提出的交通网络资源的优化配置方法能够最终确定优化的交通网络资源配置方案。

(3) 尽管实例网络的规模小，但HSTAA算法和交通网络资源的优化配置方法对大规模网络同样适用，且由于一般交通网络最多几个层次等级，所以，实际计算复杂度仍然只取决于网络本身的规模。

(4) 交通网络层次性可以作为交通网络资源优化配置的重要途径，能有效地提高交通系统性能，研究结果对可持续交通网络规划具有重要意义。

[1] 王庆云. 交通运输发展理论与实践[M]. 北京: 中国科学技术出版社, 2006: 556−559.

WANG Qing-yun. Theory and practice of transportation development[M]. Beijing: China Science and Technology Press,2006: 556−559.

[2] 段杰, 李江. 基于空间分析的城市交通网络结构特征研究[J].中山大学学报: 自然科学版, 2002, 41(6): 105−108.

DUAN Jie, LI Jiang. The structure characteristic research of urban traffic network based on spatial analysis[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2002, 41(6):105−108.

[3] 陈涛, 陈森发. 城市道路交通系统耗散结构特性的研究[J].土木工程学报, 2004, 37(1): 74−77.

CHEN Tao, CHEN Sen-fa. Study on characteristics of dissipative structure in urban traffic system[J]. China Civil Engineering Journal, 2004, 37(1): 74−77.

[4] Angeloudis P, Fisk D. Large subway systems as complex networks[J]. Physic A, 2006, 367: 553−558.

[5] 四兵锋, 赵小梅, 孙壮志. 城市混合交通网络系统优化模型及其算法[J]. 中国公路学报, 2008, 21(1): 77−82.

SI Bing-feng, ZHAO Xiao-mei, SUN Zhuang-zhi. Optimization model and its algorithm for urban mixed traffic network system[J]. China Journal of Highway and Transport, 2008, 21(1):77−82.

[6] 王媛媛, 陆化普. 基于可持续发展的土地利用与交通结构组合模型[J]. 清华大学学报: 自然科学版, 2004, 44(9):1240−1243.

WANG Yuan-yuan, LU Hua-pu. Integrated model of urban land-use and modal split based on sustainable development[J].Journal of Tsinghua University: Science and Technology, 2004,44(9): 1240−1243.

[7] 赵彤, 高自友. 交通离散网络设计与土地使用问题的组合模型与求解算法[J]. 土木工程学报, 2003, 36(7): 33−38.

ZHAO Tong, GAO Zi-you. A combined model and solution algorithm for transport discrete network design and land-use problem[J]. China Civil Engineering Society, 2003, 36(7):33−38.

[8] Taaffe E J, Morrill R L, Gould P R. Transport expansion in underdeveloped countries: A comparative analysis[J].Geographical Review, 1963, 53(4): 503−529.

[9] Tomko M, Winter S, Claramunt C. Experiential hierarchies of streets[J]. Computers, Environment and Urban Systems, 2008,32(1): 41−52.

[10] Horner M W, O’kelly M E. Embedding economies of scale concepts for hub network design[J]. Journal of Transport Geography, 2001, 9(4): 255−265.

[11] Yamins D, Rasmussen S, Fogel D. Growing urban roads[J].Networks and Spatial Economics, 2003, 3(1): 69−85.

[12] Dial R B. A probabilistic multipath traffic assignment algorithm which obviates path enumeration[J]. Transportation Research,1971, 5(2): 83−111.

[13] BELL M G H. Alternatives to Dial Logit assignment algorithm[J]. Transportation Research B, 1995, 29(4), 287−295.

[14] Leurent F. Curbing the computational difficulty of the Logit equilibrium assignment model[J]. Transportation Research B,1997, 31(4): 315−326.

[15] Huang H J. A combined algorithm for solving and calibrating the stochastic traffic assignment model[J]. Journal of the Operational Research Society, 1995, 46: 977−987.

[16] Huang H J, Li Z C. A multiclass, multicriteria Logit-based traffic equilibrium assignment model under ATIS[J]. European Journal of Operational Research, 2007, 176(3), 1464−1477.

[17] 陆化普. 交通规划理论与方法[M]. 北京: 清华大学出版社,2006: 23.

LU Hua-pu. Theory and method in transportation planning[M].Beijing: Tsinghua University Press, 2006: 23.

[18] 陆建, 胡刚. 常规公交线网布局层次规划法及其应用[J]. 城市交通, 2004, 2(4): 34−37.

LU Jian, HU Gang. Level planning method of bus-route network and its application[J]. Urban Transport of China, 2004, 2(4):34−37.

[19] 肖滨, 范炳全, 柯欣. 城市公交线网的分层规划方法[J]. 城市交通, 2005, 3(3): 19−22.

XIAO Bin, FAN Bing-quan, KE Xin. Research on a layered method of the planning on the urban transit network[J]. Urban Transport of China, 2005, 3(3): 19−22.

[20] van Nes R, Bovy P. Multimodal traveling and its impact on urban transit network design[J]. Journal of Advanced Transportation, 2004, 38(3): 225−241.

[21] 王炜, 项乔君, 常玉林, 等. 城市交通系统能源消耗与环境影响分析方法[M]. 北京: 科学出版社, 2002: 284.

WANG Wei, XIANG Qiao-jun, CHANG Yu-lin, et al. Methods for urban traffic system energy consumption and environmental impact analysis[M]. Beijing: Science Press, 2002: 284.

[22] 曾明华, 李夏苗, 刘大鹏. 城市群交通网络特性研究[J]. 系统工程, 2009, 27(3): 10−15.

ZENG Ming-hua, LI Xia-miao, LIU Da-peng. Properties analyses of urban agglomeration traffic networks[J]. Systems Engineering, 2009, 27(3): 10−15.

(编辑 陈灿华)

Optimal allocation approach of transport network resource based on hierarchical property

ZENG Ming-hua1, LI Xia-miao2

(1. School of Railway Tracks and Transportation, East China Jiaotong University, Nanchang 330013, China;2. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Hierarchical property of transport network as a common phenomenon was introduced to design traffic assignment algorithm and to study optimal allocation approach for transport network resource. After the analyses of algorithm design bases, a definition of hierarchy factor was formulated, which was determined by utilizing transport network topologies or traffic correlation strength between each traffic zone where traffic nodes located. Based on the typical Dial’s traffic assignment algorithm, a hierarchy-based stochastic traffic assignment algorithm (HSTAA) was proposed applying hierarchical property represented mainly by hierarchy factors. The HSTAA was furtherly verified and analyzed through a case study. The results show that the total impedance of the transport network obtained by HSTAA decreases when upgrading the hierarchical level of link in the higher level and is less than that by Dial’s traffic assignment algorithm when the hierarchy factors are controlled in a certain domain, and that the total exhaust emission of the transport network obtained by HSTAA increases when upgrading the hierarchical level of link in the higher level and is anyhow less than that by Dial’s traffic assignment algorithm. The allocation of transport network resources can be effectively optimized and adjusted through controlling reasonably the network hierarchical level. All of the aforementioned investigations have finally contributed to the optimal allocation approach of the transport network resources.

transport network; optimal allocation; hierarchical property; hierarchy factor; Dial’s traffic assignment algorithm

U491

A

1672−7207(2011)01−0247−07

2009−10−12；

2009−12−20

国家自然科学基金资助项目(71071165)

李夏苗(1963−)，男，湖南茶陵人，博士，教授，从事交通运输规划与管理、物流工程研究；电话：13787018526；E-mail: xmli@mail.csu.edu.cn