尾矿坝地震稳定性分析的区间模型及应用
董陇军,赵国彦,宫凤强,李志国
(中南大学 资源与安全工程学院,湖南 长沙,410083)
尾矿坝地震稳定性分析的区间模型及应用
董陇军,赵国彦,宫凤强,李志国
(中南大学 资源与安全工程学院,湖南 长沙,410083)
在尾矿坝地震稳定性分析中,为适应计算参数本身具有的随机性和未确知性,将计算参数转换成盲数形式;针对尾矿坝地震稳定的极限平衡分析问题,提出一种计算尾矿坝安全系数的新方法,并将该模型应用到某尾矿坝的地震稳定性分析中。实际分析结果表明:运用盲数运算法则可以计算稳定性系数在不同取值区间内的可信度,克服了传统方法描述过于绝对化的问题,为判断尾矿坝的稳定状态提供了更全面的依据;该尾矿坝边坡安全系数低于1.3的可能性为13%,即在发生烈度为Ⅶ度的地震时该尾矿坝安全的可能性为87%,失稳的可能性较小,与实际情况相吻合;盲数理论在尾矿坝地震稳定性分析中能更好地考虑参数的不确定性,完善了尾矿坝稳定性分析理论,为尾矿坝稳定性的分析提供了一条新的途径。
尾矿坝工程;区间分析模型;盲数;地震稳定性;安全系数
尾矿坝工程中物理力学参数的选取是一个复杂的问题,存在大量的不确定性因素。稳定性分析所涉及的参数如黏聚力、内摩擦角、重度等往往不是定值,属于不确定性信息。在传统的尾矿坝地震稳定性的分析中,大多是按照经验,忽略了计算参数的未确知性,将不确定性问题作为确定性问题考虑[1−7]。这些不确定
性信息包括随机性、模糊性、灰性、未确知性等,相应的表达处理理论为概率统计、模糊数学、灰色数学、未确知数学等。如何全面考虑这些不确定性信息,提高计算的可靠性成为工程技术人员关心的问题,为此,许多研究者进行了大量地探索和研究[8−16]。刘开弟等[17]建立了未确知数学的理论体系,董陇军等[5−9]将未确知测度理论发展到边坡的地震稳定性分析、膨胀土等级判定、采空区危险性评价、围岩稳定性分析等领域,取得了较好的效果。李朝甫等[2]将灰色系统理论用于滑坡位移分析中;徐卫亚等[3]将模糊集理论应用到边坡稳定分析常用的极限平衡方法中,建立了稳定性分析的模糊计算方法;周建普等[4]将边坡定值分析法与可靠性方法结合,考虑土性参数的变异性和不确定性。赵志峰等[1]将盲数理论应用到边坡安全稳定分;析研究中。但是,这些研究大都是边坡工程方面的,关于尾矿坝方面的研究较少。实际情况的限制和地质条件的复杂性使得很难对岩土体进行大量、准确的试验,从而难以得到参数的准确值或概率分布,因此,在使用模糊数学等方法的过程中难以确定参数值合理的隶属函数,给求解带来了困难[1]。灰色理论中区间型灰数多是定义在一个区间内,可靠性分析方法也需要用大量的试验资料来确定参数的变异性等不确定性指标。考虑到以上问题以及尾矿坝工程中参数的不确定性往往是多种不确定性(如模糊性和随机性)的混合;因此,采用一种新的数学方法来表达多种信息的不确定性显得尤为必要,即可以表示含有随机性、模糊性、灰性及未确知性中2种或2种以上不确定性的信息[17],在这方面盲数理论提供了较好的思路。在此,本文作者基于极限平衡分析方法及盲数理论建立尾矿坝地震稳定性分析的区间模型。
1 盲数的基本原理
盲数是未确知数学中用于表达和处理同时具有 2种或2种以上不确定性信息的数学工具[17]。
1.1 盲数的定义
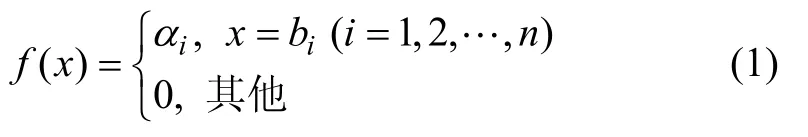
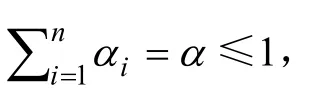
1.2 盲数的期望值
设a和b为实数,且a≤b。称(a+b)/2为区间型灰数[a,b]的“心”,记作 Θ[a ,b]= (a+b)/2。若f(x)为盲数,且表达形式见式(1),则盲数f(x)的期望值可以表示为

1.3 盲数的四则运算
设A与B为盲数,以加法为例,表1中称A与B为可能值带边和矩阵,由小到大排列的实数列x1,x2, …,xk和y1,y2, …,ym分别称为A与B的可能值序列,且分别称为带边矩阵的纵边和横边,互相垂直的直线分别称为带边矩阵的横轴和纵轴。

表1 A与B的可能值带边和矩阵Table 1 Sum matrix of A and B for probability
对照盲数加法定义,只需把和运算中的可能值带边和矩阵中的“和”改为相应的减、乘、除,从而把可能值带边和矩阵变为可能值带边减、乘、除矩阵,其他不变,即可得到未确知有理数积的定义。
1.4 盲数的可信度计算
表 2所示为A和B的可信度带边积矩阵,f(x1),f(x2), …,f(xk)和g(y1),g(y2), …,g(ym)分别称为A和B的可信度序列,且分别称为带边矩阵的纵边和横边,互相垂直的直线分别称为带边矩阵的横轴和纵轴。
设A和B为盲数,分别表示为分布密度形式,即

表2 A和B的可信度带边积矩阵Table 2 Product matrix of A and B for reliability

则事件A/B≥r的可信度表示为

式中:B表示某一评价标准的分级阈值,一般为实数值形式;r是按实际问题要求而确定的某个已知实数。
2 地震荷载下尾矿坝稳定性分析的区间模型
尾矿坝的设计以及安全评价过程中均需要进行地震情况下的稳定性验算。地震附加荷载可分解为水平附加荷载Ei和竖向附加荷载Ei′,计算公式分别为:

式中:C为地震综合影响系数,常取用C=0.25;Wi为第i分条的质量;ai和ai′分别为水平与竖向地震加速度分布系数;Kc表示水平地震系数,为地面最大地震平均加速度与重力加速度之比,即 Kc=ai/g;表示竖向地震系数,=2Kc/3。
根据已有研究成果及规程[18],对于土质或岩质边坡,其变形破坏模式可按圆弧形破坏方式进行研究[1]。对尾矿坝而言,在其正常运行期间,浸润线通常介于最危险滑动面和坡面之间,此时的尾矿坝稳定性验算必须考虑浸润线的影响,下面给出此种最常见情况下结构抗力A以及荷载效应B的计算公式。
为尽可能得到最精确的计算结果,需考虑动水力的作用。但是,动水力方向与垂直分条的竖直方向并不一致,故不能简单地套用土条重力的处理方法。实际上,采用圆弧法分析边坡稳定性本质上是考量滑动力矩与抗滑力矩的相对大小,考虑动水力时的尾矿坝结构抗力及荷载效应表达为抗滑力矩和滑动力矩。由于动水力的位置和作用方向均容易确定,因此,运用力矩进行处理还起到了简化分析计算的效果。
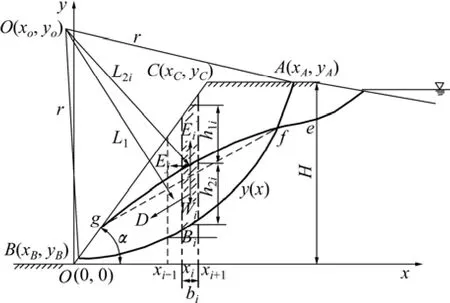
图1 考虑地震和浸润线作用的尾矿坝圆弧破坏剖面图Fig.1 Slope section of arc of destruction considering impact of tailings dam infiltration and seism
如图1所示,坡面方程为g(x),圆弧形滑动面方程为y(x),浸润线efg的方程为ω(x)。设浸润线、坡面以及圆弧滑动面所围部分(fgBf)的面积为W,作用在这部分坝体上的动水力合力为D,则D的作用点在面积fgBf的形心,作用方向可假定与fg平行(如图中箭头所示),动水力对滑动面圆心的力臂为L1。h1i和h2i分别表示采用垂直分条分析尾矿坝稳定性时浸润线之上部分与浸润线之下部分的土条长度。动水力可按下式计算:

式中:GD表示作用在单位体积坝体上的动水力;w为水的重度;I为在面fgBf范围内的水头梯度平均值,可近似假设I等于fg连线的坡度。
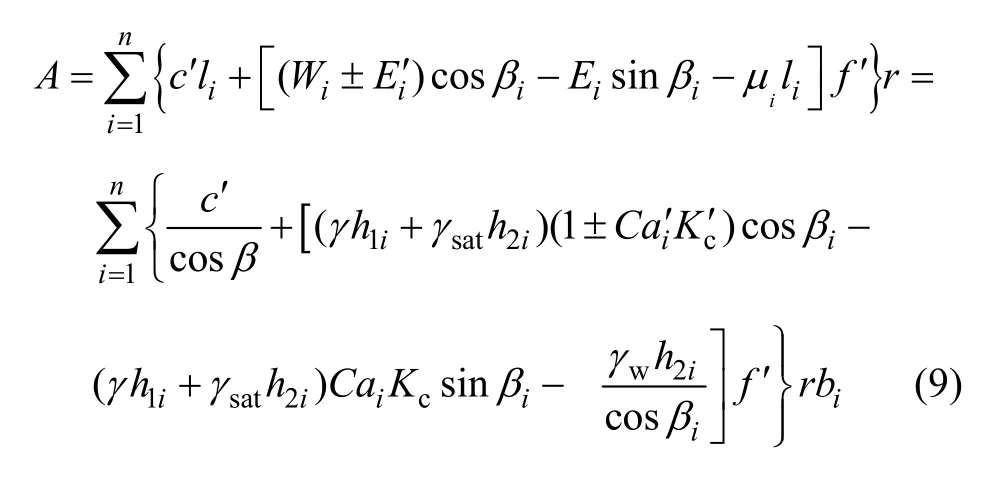
实际计算第i个土条的质量Wi时,若计算抗滑指标,则在浸润线之下部分应考虑水的浮力作用;若计算滑动指标,则采用饱和容重。于是,考虑浸润线后的尾矿坝结构抗力A的计算公式可表示为:式中:i为第i分条底面与水平面的夹角;li为第i分条底面弧长;Wi为第i分条质量; 和sat分别为尾矿天然重度和饱和重度;c′和f′分别为尾砂的有效粘聚力和有效内摩擦因数。

荷载效应B的计算公式可表示为:尾矿坝结构抗力A和荷载效应B的区间数分别为:
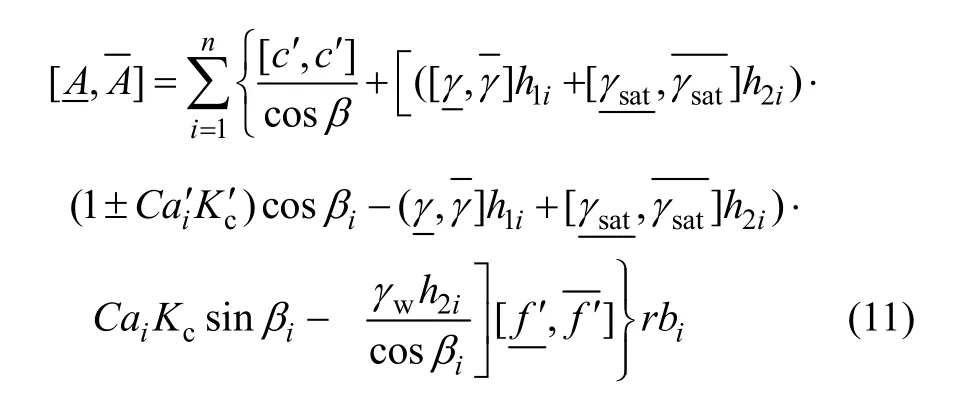

3 实例应用研究
某尾矿库的等级为二等库,堆积坝尾矿主要由尾细砂、尾粉砂、尾粉土和尾粉质黏土堆积而成,局部出现少量尾中砂。其地震基本烈度为Ⅶ度。采用上游法堆坝,堆积边坡为1:6。最终总坝高210 m,最终堆积标高为1.3 km,总库容为1.84×108m3,有效库容为1.6×108m3,依据该尾矿坝的工程勘察报告,尾矿坝的物理力学参数见表3[16]。
根据式(11~13),经计算得:尾矿坝安全系数F的取值介于0.91与1.10之间的可能性为3%;介于1.11与1.29之间的可能性为10%;介于1.30与1.97之间的可能性为53%;介于1.98与2.86之间可能性为27%;介于2.87与3.22之间的可能性为0.07。通过以上分析可见:该尾矿坝安全系数取值在1.30以下的可能性为13%。与传统极限分析定值方法相比,这种表示方式全面地反映了在各个不同取值区间的可能性,避免了由于参数取值单一而造成的计算安全系数时的偏差,从而能更全面地判断边坡的安全稳定状态,完善了尾矿坝稳定性分析理论。
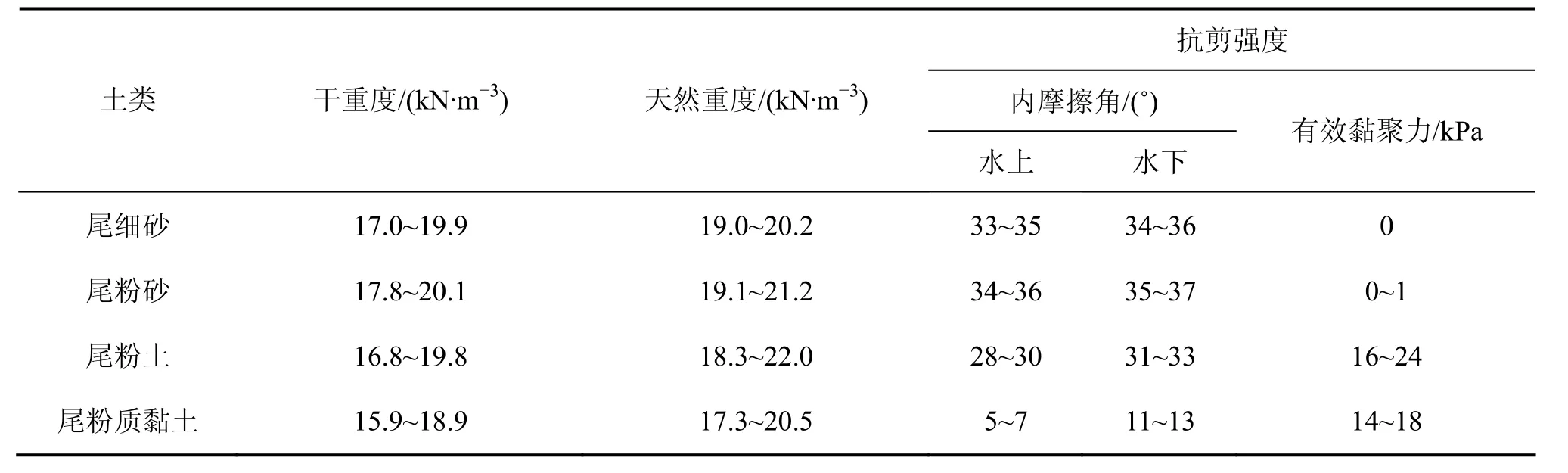
表3 尾矿坝物理力学参数Table 3 Physical and mechanical indicators of tailings dam
根据该尾矿坝边坡工程的重要性等级和《规程》[18],此尾矿坝边坡的允许安全系数可以取为1.30。采用式(3)可以计算出F小于 1.30的概率为P(F>1.3)=0.03+0.10=0.13=13%,由此可知,该尾矿坝边坡安全系数低于1.3的可能性为13%,即在发生烈度为Ⅶ度的地震时该尾矿坝的安全性为87%,失稳的可能性较小,这一点与实际情况相吻合。在2008—08—30,该尾矿坝所在区域也发生了5.0级地震,坝体稳定性良好,未发生滑坡或失稳现象。尽管尾矿坝目前安全状况较好,但也存在一定的风险,主管部门要重视尾矿坝的安全设施的维护,在后期筑坝的过程中应该采取更加合理的筑坝方式,增强坝体的稳定性。
4 结论
(1) 针对实际尾矿坝工程中参数的不确定性和试验资料的有限性,基于极限平衡分析方法及盲数理论建立了尾矿坝稳定性分析的区间模型。该模型可以充分考虑分析中所涉及的计算参数的不确定性,将安全系数用盲数形式表达。
(2) 与传统极限平衡分析方法相比,尾矿坝地震稳定性分析的区间模型可以实现将安全系数可能的各种情况用可信度表示,从而得到较为全面的结果,给安全稳定评判提供了较充分的依据,完善了尾矿坝稳定性分析理论。
(3) 该尾矿坝边坡安全系数低于 1.3的可能性为13%,表明存在一定的风险,主管部门要重视尾矿坝的安全设施的维护,在后期筑坝的过程中应该改进的筑坝方式,加强浸润线的观测,以便增强坝体的稳定性。
(4) 盲数理论在在尾矿坝稳定性分析中的研究还只是初步尝试,在今后的研究工作中,在如何更为有效地确定合理的力学参数取值区间、条分数等问题方面有待进一步研究,以增强该方法在实际工程中的适用性和可推广性。
[1] 赵志峰, 徐卫亚. 基于盲数理论的边坡安全稳定分析研究[J].岩土力学, 2007, 28(11): 2401−2404.
ZHAO Zhi-feng, XU Wei-ya. Slope stability analysis based on the blind data theory[J]. Rock and Soil Mechanics, 2007, 28(11):2401−2404.
[2] 李朝甫, 徐迎, 谭跃虎, 等. 灰色系统理论在滑坡位移分析中的应用[J]. 系统工程理论与实践, 2002(2): 129−132.
LI Chao-fu, XU Ying, TAN Yue-hu, et al. Application of grey system theory to analyzing displacement information of slide[J].Systems Engineering Theory & Practice, 2002(2): 129−132.
[3] 徐卫亚, 蒋中明, 石安池. 基于模糊集理论的边坡稳定性分析[J]. 岩土工程学报, 2003, 25(4): 409−413.
XU Wei-ya, JIANG Zhong-ming, SHI An-chi. Slope stability analysis using fuzzy sets theory[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 409−413.
[4] 周建普, 李献民, 王永和. 黏土边坡可靠性分析方法研究[J].湖南大学学报: 自然科学版, 2002, 29(5): 92−97.
ZHOU Jian-pu, LI Xian-min, WANG Yong-he. Research for method of reliability analysis for clayey soil slope[J]. Journal of Hunan University: Natural Sciences, 2002, 29(5): 92−97.
[5] 董陇军, 王飞跃. 基于未确知测度的边坡地震稳定性综合评价[J]. 中国地质灾害与防治学报, 2007, 18(4): 74−78.
DONG Long-jun, WANG Fei-yue. Comprehensive evaluation on seismic stability of slopes based on unascertained measurement[J]. The Chinese Journal of Geological Hazard and Control, 2007, 18(4): 74−78.
[6] DONG Long-jun, PENG Gang-jian, FU Yu-hua, et al.Unascertained measurement classifying model of goaf collapse prediction[J]. Journal of Coal Science & Engineering, 2008,12(2): 221−224.
[7] 董陇军, 李夕兵, 宫凤强. 膨胀土胀缩等级分类中的未确知均值聚类模型及应用[J]. 中南大学学报: 自然科学版, 2008,39(5): 1075−1080.
DONG Long-jun, LI Xi-bing, GONG Feng-qiang. Unascertained average clustering method for classification of grade of shrink and expansion for expansive soils and its application[J]. Journal of Central South University: Science and Technology, 2008,39(5): 1075−1080.
[8] 董陇军, 李夕兵, 宫凤强. 开采地面沉陷预测的未确知聚类预测模型[J]. 中国地质灾害与防治学报, 2008, 19(2): 95−99.
DONG Long-jun, LI Xi-bing, GONG Feng-qiang.Comprehensive evaluation on seismic stability of slopes based on unascertained measurement[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(2): 95−99.
[9] DONG Long-jun, HU Da-tao, BAI Yun-fei. Unascertained average grade model for surrounding rock classification on hydraulic tunnels[C]//2008 International Symposium on Safety Science and Technology: Progress in Safety Science and Technology (Vol. VII). Beijing: Science Press, 2008: 2227−2231.
[10] 李文秀. 岩石力学中的 Fuzzy数学方法[J]. 力学学报, 1990,22(3): 328−336.
LI Wen-xiu. Fuzzy mathematic method in rock mechanics[J].Chinese Journal of Theoretical and Applied Mechanics, 1990,22(3): 328−336.
[11] 潘家铮. 建筑物的抗滑稳定和滑坡分析[M]. 北京: 水利出版社, 1980: 10−35.
PAN Jia-zheng. Stability and slope analysis of building[M].Beijing: Water Conservancy Press, 1980: 10−35.
[12] 张国祥, 刘宝琛. 潜在滑面理论及其在边坡分析中的应用[M].长沙: 中南大学出版社, 2003: 5−20.
ZHANG Guo-xiang, LIU Bao-chen. Potentially sliding surface theory and application in the slope analysis[M]. Changsha:Central South University Press, 2003: 5−20.
[13] 王贵成, 曹平, 林杭, 等. 用灰色理论确定边坡最优监测点及安全系数[J]. 中南大学学报: 自然科学版, 2007, 38(3):574−578.
WANG Gui-cheng, CAO Ping, LIN Hang, et al. Determination of optimum monitoring point of slope and safety factor using grey system theory[J]. Journal of Central South University:Science and Technology, 2007, 38(3): 574−578.
[14] 张世文, 王红艳. 影响尾矿坝安全稳定性因素分析及对策[J].矿业工程, 2004, 2(2): 61−63.
ZHANG Shi-wen, WANG Hong-yan. Analysis of factors influencing stability of tailing dam and measures for improving dams stability[J]. Mining Engineering, 2004, 2(2): 61−63.
[15] 吴中如. 水工建筑物安全监控理论及其应用[M]. 南京: 河海大学出版社, 1990: 5−10.
WU Zhong-ru. Security monitoring theory and application of hydraulic structure[M]. Nanjing: Hohai University Press, 1990:5−10.
[16] 王飞跃. 基于不确定理论的尾矿坝稳定性分析及综合评价研究[D]. 长沙: 中南大学土木建筑学院, 2008: 90−120.
WANG Fei-yue. Research on stability analysis and comprehensive assessment of taings dam based on the uncertainty theory[D]. Changsha: Central South University.College of Architecture and Civil Engineering, 2008: 90−120.
[17] 刘开弟, 吴和琴, 庞彦军, 等. 不确定性信息数学处理及应用[M]. 北京: 科学出版社, 1999: 1−190.
LIU Kai-di, WU He-qin, PANG Yan-jun, et al. Mathematics processing of unascertained information and its application[M].Beijing: Science Press, 1999: 1−190.
[18] AQ 2006—2005. 尾矿库安全技术规程[S].AQ 2006—2005. Technical specification for tailings dam safety[S].
(编辑 赵俊)
Interval analysis model of tailings dam seismic stability and its application
DONG Long-jun, ZHAO Guo-yan, GONG Feng-qiang, LI Zhi-guo
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
The calculation parameters including the mixture of multi uncertainty were transformed to the blind data to express the uncertainty of the calculation parameters in the tailings dam engineering. The theory of blind information was applied to the rigid limiting equilibrium method for tailings dam seismic stability. A new method of safety factor was applied to the seismic stability analysis of a tailings dam. The results show that the corresponding confidence level of safety factor at different numerical value intervals can be calculated by blind data algorithms. The more comprehensive result is provided to judge the stability state of tailings dam consequently, overcoming the defect of absolutely definitive description in the traditional methods. The tailings dam slope safety factor is less than 1.3, and the corresponding possibility is 13%, indicating that the probability of the tailing dam safety is 87% in the event of seismic intensity of Ⅶdegrees, which is consistent with the actual situation. It is a new way to analyze seismic stability of tailing dams, and the result is more detailed and reliable.
tailings dam engineering; interval analysis model; blind data; seismic stability; safety factor
TV649;TD926.4
A
1672−7207(2011)01−0164−06
2010−09−06;
2010−12−21
国家自然科学基金资助项目(50934006);中南大学学位论文创新项目(1343-74335000020)
董陇军(1984−),男,甘肃陇西人,博士研究生,从事采矿与岩土工程可靠性及灾害控制研究;电话:18711191205;E-mail: csudlj@163.com

