基于局部回归的色谱保留时间对齐可逆算法

李龙，张纪阳,，史秀建，孙汉昌，谢红卫，欧阳辰星

(1. 国防科学技术大学 机电工程与自动化学院，湖南 长沙，410073；2. 北京蛋白质组研究中心 蛋白质组学国家重点实验室，北京，102206；3. 中南大学 商学院，湖南 长沙，410083)

基于局部回归的色谱保留时间对齐可逆算法

李龙1，张纪阳1,2，史秀建1，孙汉昌1，谢红卫1，欧阳辰星3

(1. 国防科学技术大学 机电工程与自动化学院，湖南 长沙，410073；2. 北京蛋白质组研究中心 蛋白质组学国家重点实验室，北京，102206；3. 中南大学 商学院，湖南 长沙，410083)

提出并实现一种基于局部回归的对齐算法，选择鉴定结果最多的一次实验作为参考，实现色谱保留时间的可逆对齐，将n次实验的对齐建模次数从n(n−1)/2次减少为n−1次。该算法还实现不同实验间色谱保留时间的非线性对齐，并且能够克服少量从色谱柱中多次流出肽段的影响。研究结果表明：该方法计算时间复杂度远比现有算法的低，对齐精度也能够满足后续计算的需要。

液质联用串联质谱；定量蛋白质组学；色谱保留时间对齐；局部回归；可逆算法

基于液相色谱−串联质谱(LC-MS/MS)的无标记(label free)定量是蛋白质定量分析的核心技术之一[1−2]，特别是基于高精度质谱仪(例如热电公司的LTQ-FT[3]和LTQ-Orbitrap[4])的分析平台在大规模生物标志物发现中已经广泛应用[5−9]。LC-MS/MS实验可以同时鉴定、定量肽段，但是由于受分析能力的限制，只能根据“动态排除”策略，选择部分母离子进行MS/MS分析，所以，肽段的鉴定结果具有很大的随机性[10]。有研究表明，2次重复实验(技术重复，每次重复又称为一次LC-run)之间重叠鉴定的肽段只有60%～70%[11]；所以，对同一样本重复分析成为克服随机采样效应的重要方法。MS图谱中的信号重复性远优于MS/MS分析的重复性，超过 95%的离子流色谱峰(Extracted ion chromatograms, XIC)在重复实验中都会出现[12]；因此，在数据分析中利用色谱保留时间对齐实现重复实验和不同样品的 LC-MS分析中的信号对应，可以克服 MS/MS分析的随机效应，充分利用实验数据。色谱保留时间对齐(Retention time alignment)一般是利用2次实验间共同鉴定的肽段来建立色谱保留时间对齐模型，然后，利用该模型预测那些在实验中未鉴定肽段的色谱保留时间[13]。考虑影响色谱分析重复性的复杂因素，一般采用非线性模型建立2次实验间色谱保留时间的关系。常用的模型有3次样条、局部回归、小波基、相关函数、偏移向量等[14]。在处理多次重复实验的数据时，一般采用两两对齐或者寻找参考LC-run的方法[15]。两两对齐一般要计算量大，而参考 LC-run方法需要找到一个能够包含所有信号的LC-run，对于随机性较大的MS/MS分析来说，十分困难。由于很多非线性模型都不是可逆的，为了实现2次实验间的色谱保留时间对齐，需要建立2个模型，增加了计算量和计算复杂程度。在此，本文作者基于局部回归方法实现一个可逆的色谱保留时间对齐模型。利用该模型，提出一种使用参考LC-run的色谱保留时间对齐策略，解决了任何一次实验都只能鉴定部分肽段、不适合作为参考LC-run的问题，提高了计算速度。

1 质谱定量分析典型流程

在基于无标记定量的生物标志物发现过程中，利用质谱对目标样本和对照样本分别进行分析，找出不同质谱信号的差异以及其代表的蛋白质，实现相对定量[16]。目前，基于高性能质谱平台的无标记定量分析主要有 2种典型的实验策略：LC-MS策略和LC-MS/MS策略[17]。其中 LC-MS策略直接分析蛋白质混合物酶切(一般使用胰酶)得到的肽段混合物，得到以整体肽段离子的质荷比(Mass to charge ratio,m/z)和信号强度为基本元素的一级质谱图(MS图谱)，然后，在数据分析中直接解析MS图谱中的同位素峰，构建肽段的离子流色谱峰，进行肽段定量(肽段序列未知)。这种方法不直接利用质谱鉴定肽段，而是利用MS图谱中的信号来表征肽段。与之不同的是：LC-MS/MS策略进行一般的鸟枪法实验(Shotgun)，肽段在进行MS分析后，还要选择母离子(Precursor ions)进行惰性气体诱导碰撞碎裂(Collision-induced dissociation, CID)，得到包含肽段序列信息的MS/MS图谱。在数据处理中，首先利用 MS/MS图谱鉴定肽段序列，然后利用MS图谱中的母离子信号实现肽段的定量。这种方法的最大优势在于可以同时实现肽段的鉴定和定量，2种策略的最大差异是是否进行MS/MS分析。无论是哪种策略，都需要将不同实验得到的质谱信号进行对比，色谱保留时间是实现信号对齐的重要参数[11]。本文作者针对LC-MS/MS策略进行研究，其实验和数据分析流程可以用图1来概括[13]。可以看出：在数据分析中，色谱保留时间的对齐是重要的一步。

图1 典型无标记定量的实验和数据分析流程Fig.1 Typical workflow of experiment and data processing for label free quantification in proteomics

2 数据和方法

本文所使用的数据来自文献[18]，酵母(Saccharomyces cerevisiae, Type Ⅱ, Sigma)经过样品处理后，利用配备有Agilent 1100(Agilent Technologies,Palo Alto, CA)高效液相色谱(HPLC)的LTQ/FT质谱仪(Thermo Electron, San Jose, CA)进行10次重复实验。在质谱分析中，采用了LC-MS/MS策略，1次MS分析之后紧跟着进行10次MS/MS分析，采用30 s动态排除和自动增益控制(Auto gain control, AGC)。得到的数据使用SEQUEST搜库(Bioworks 3.2版本)，使用诱骗数据库搜索(Decoy searching)策略来对搜库结果进行假阳性率(False discovery rate, FDR)控制，使用1%FDR的标准过滤搜库结果。得到的搜库结果去冗余，然后，提取肽段色谱保留时间并对齐。另外，为了验证重复实验间色谱保留时间的非线性关系，还利用一个上样量(loading amount)不同的2次重复实验数据，实验方法与参考文献[18]中的相同。

色谱保留时间对齐采用局部回归方法(Local regression)，10次重复实验之间对齐采用下列步骤：

(1) 首先利用肽段鉴定结果提供的质荷比、序列和MS/MS图谱扫描号(Scan number)在单个LC-run得到的原始数据(raw文件)中提取离子流色谱峰，得到肽段的色谱保留时间。

(2) 找出原始数据文件最大的那次 LC-run(预期包含信息最多)作为参考，其他9次实验的色谱保留时间均采用局部回归方法向参考实验对齐，同时记录局部回归的模型参数。

(3) 参考实验中的所有肽段(对齐和鉴定)向其他9次实验进行色谱保留时间对齐。这一步可以利用已经建立的局部回归可逆模型，不需再建模。

(4) 输出色谱保留时间对齐结果，并且进行其他定量分析。

从上面的步骤可以看出：采用局部回归方法进行可逆的保留时间对齐，关键要保证模型是可逆的，这样只需要建立和记录9个模型，进行18次对齐计算，就可以实现10次实验之间的对齐。而两两对齐的不可逆模型则需要建立=45个模型，进行45次对齐计算。一般来说，对于n次重复实验，若采用两两对齐方法，则需要建立=n(n− 1)/2个模型，而若采用可逆对齐方法，则只需要建立n−1个模型，可以看出本文使用的模型将会大大减少计算量，重复实验次数越多，效果越明显。另外，本文采用的LOWESS模型是局部线性模型，也是局部回归中最简单的一种，算法自身的计算量也得到了控制[19]。为了排除异常值数据点的影响，在计算局部最小二乘回归时，采用鲁棒(Robust)方法[19]，整个算法如下所示，算法的收敛性等性能分析见文献[19]。

算法1：鲁棒局部回归算法。

步骤1：输入。

(1) 参考实验和其他任意一次实验的共同鉴定肽段的色谱保留时间TR向量，x=rTR和y=xTR；

(2) 局部回归窗口大小span，参考数据点向量数目ref_num，最大迭代次数iter；

步骤2：初始化变量。

步骤3：开始局部回归Local regression。

(1) 计算窗口范围：

(2) 提取窗口范围内的数据点，并且统计数据点数目sub_num；

(3) 若num小于 4，sub_min=sub_min−binW，sub_max=sub_max+binW，则返回步骤 3中(2)，否则进行下一步，得到的数据点集合称为S；

(4) 假设得到的局部数据点为sub_x，sub_y，求每个数据点的权重：

(5) 进行加权最小二乘回归(WLS)：

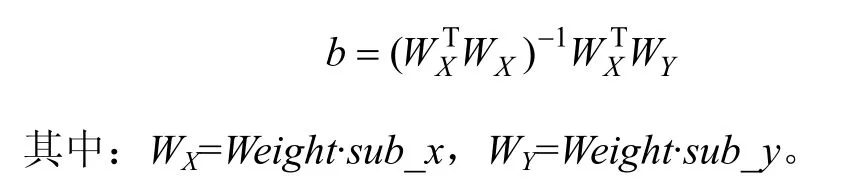
步骤4：迭代进行Robust回归。

(1) 计算残差：

(2) 对残差进行归一化处理：

其中：median表示求取中值。

(3) 计算权重因子：

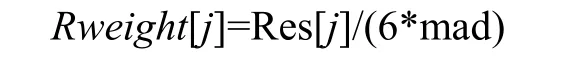
若Rweight[j]=1，则Rweight[j]=0，进行变换：Rweight[j]=1−Rweight[j]*Rweight[j]，其中j∈S；

(4) 更新权重：W_new[j]=Weight[j]*Rweight[j]，其中j∈S；

(5) 记录回归参数，bold=b，重新进行WLS：

其中：WX=W_new·sub_x，WY=W_new·sub_y；

(6) 迭代次数+1，若超过预设迭代次数iter，则退出循环，否则计算差值：e=|b−bold|；若e＜ε(例如1×10−6)，则退出循环，否则跳转到步骤4中(1)。

得到局部线性模型参数，结束计算。

3 算法性能验证与讨论

在实现色谱保留时间对齐之后，还要利用对齐得到的色谱保留时间，提取未鉴定肽段的离子流色谱峰；所以，尽量减小色谱保留时间的误差，缩小搜索范围，提高色谱保留时间参数区分不同肽段的能力，可以减少假阳性结果。为了验证局部回归方法的建模效果，使用2个最大的数据文件，分析局部回归方法的色谱保留时间对齐的残差，结果如图2所示。从图2可以看出：残差符合正态分布，均值为0，标准差为0.112(时间单位为min)，相对于一般的离子流色谱峰的范围(2 min左右)，误差区间比较小。考虑到数据点集中存在噪声数据点，残差分布并不能严格通过正态性检验(例如 Jarque-Bera检验)，这也正是在局部回归中引入鲁棒迭代回归排除异常值点的原因。

图2 局部回归残差分布Fig.2 Residual distribution of local regression

局部可逆回归的最大优势在于可以大大节省计算时间。对于 10次重复的实验数据，利用 C++语言编写的算法来测试运算时间，发现在HP 6520s计算机上(Intel T5870 2.0G双核 CPU，2Gb内存)，仅仅需要10.07 s，而采用3次样条平滑方法则需要184.94 s[16]，大约是局部回归方法的 18倍。即使采用局部回归算法，若不利用可逆特性，则大约需要22 s，是本文提出算法的2倍。经过测试，那些基于LC-MS策略(把LC-MS/MS数据当作 LC-MS数据分析，包括MSInspect[12]，MSAlign[20]和 XCMS[21])的对齐算法则需要更长的运算时间。可以看出：可逆局部回归方法可以大大减少运算时间，在更大数据集上的作用会更加明显。

设计严密的技术重复实验之间色谱保留时间的非线性关系并不是很明显，这一点可以从图 3(a)中看到(其中，TR为色谱保留时间)。但是，在生物标志物发现的实际应用中，往往需要对比不同样品。由于色谱分离中不同组分之间的交互作用，色谱保留时间之间的非线性对应关系就会比较明显[22]。图3(b)所示是LC分析时间为60 min时，不同上样量情况下色谱保留时间的对齐关系，可以发现有明显的非线性效应。所以，采用局部回归方法来描述这种非线性关系也是必须的。

另外，在LC时间为60 min的数据分析中，发现最后10 min分析时间中存在一些异常数据点，在上样量为3.0 μg/μL的分析中，其色谱保留时间都大于50 min；而在上样量为0.3 μg/μL的分析中，这些肽段的色谱保留时间小于50 min，远远偏离了2次实验间色谱保留时间的基本线性关系，如图 4(a)所示。分析实验过程发现：最后10 min为色谱柱冲洗时间，若样品上样量比较大，则还会有一些在以前已经鉴定的肽段被洗脱和鉴定，就出现了双离子流色谱峰；而在上样量比较小时，冲洗过程中很难再鉴定这些已经洗脱过的肽段，残留已经不能达到质谱仪的检测灵敏度门限。所以，本文实现的局部回归方法考虑了这一问题，冲洗时间的色谱保留时间对齐采用洗脱时间段最后1个局部线性模型代替，而不利用实验数据建模，这样就避免了这个问题。图4(b)给出了相关结果。

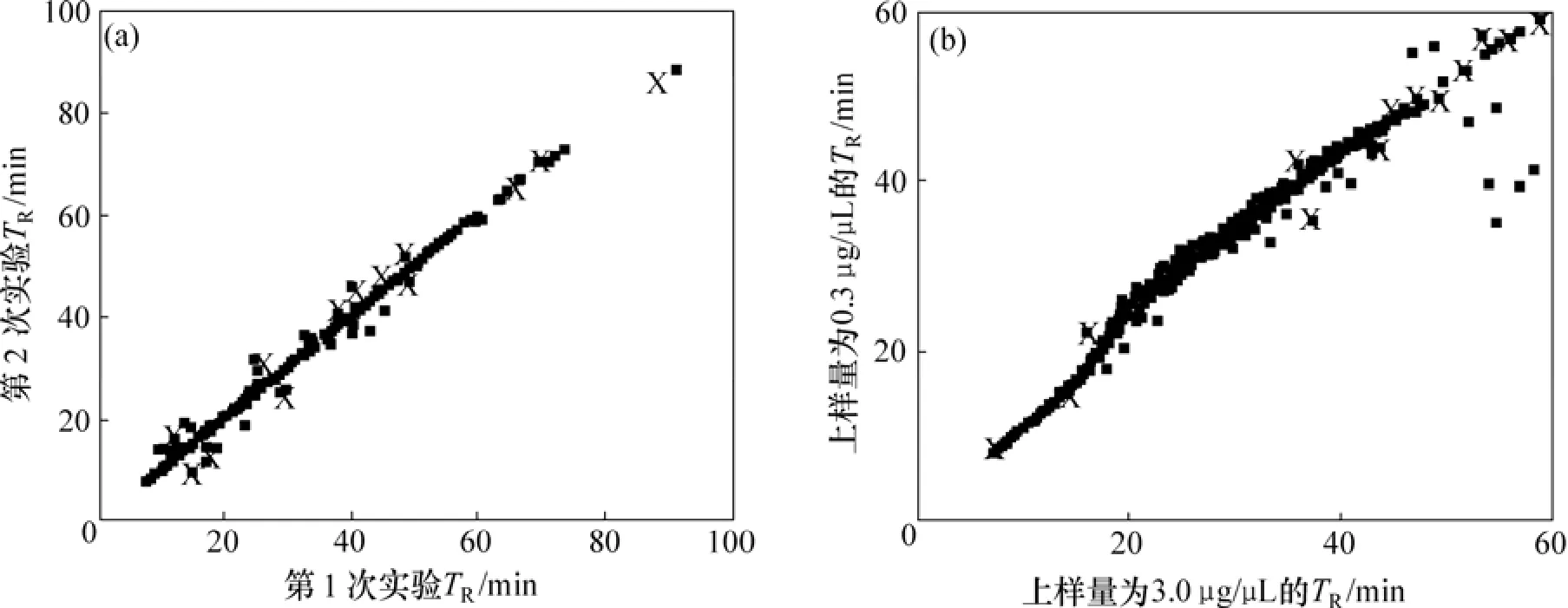
图3 不同实验条件下色谱保留时间对齐的非线性效应Fig.3 Nonlinear effect of TR alignment in different experiment conditions

4 结论

(1) 基于局部回归方法实现了一个可逆的色谱保留时间对齐模型，给出了算法流程，并且实现了该算法。

(2) 利用色谱保留时间对齐的可逆模型，提出了一种使用参考LC-run的色谱保留时间对齐策略，对齐模型只需要建立n个(n为重复实验次数)，对齐计算只需要进行2n次，就能够实现LC-MS/MS策略中的色谱保留时间对齐，解决了任何一次实验都只能鉴定出部分肽段、不适合作为参考LC-run的问题，并且提高了计算速度。

(3) 利用10次技术重复的LTQ/FT数据，发现对齐精度能够满足现阶段离子流色谱峰提取的需要。利用不同上样量的实验数据，分析和验证了色谱保留时间对齐的非线性问题。

[1] Wang M, You J, Bemis K G, et al. Label-free mass spectrometry-based protein quantification technologies in proteomic analysis[J]. Briefings in Functional Genomics, 2008,7(5): 329−339.

[2] 薛晓芳, 吴松锋, 朱云平, 等. 蛋白质组学研究中的无标记定量方法[J]. 中国生物化学与分子生物学报, 2006, 22(6):442−449.

XUE Xiao-fang, WU Song-feng, ZHU Yun-ping, et al.Label-free protein quantification methods in proteomics research[J]. Chinese Journal of Biochemistry and Molecular Biology, 2006, 22(6): 442−449.

[3] Olsen J V, De Godoy L M, Li G Q, et al. Parts per million mass accuracy on an orbitrap mass spectrometer via lock mass injection into a C-trap[J]. Molecular & Cellular Proteomics.2005, 4(12): 2010−2021.

[4] Hu Q, Noll R J, Li H, et al. The orbitrap: A new mass spectrometer[J]. Journal of Mass Spectrometry, 2005, 40(4):430−443.

[5] PENG Xin-qing, WANG Fei, GENG Xin, et al. Current advances in tumor proteomics and candidate biomarkers for hepatic cancer[J]. Expert Review of Proteomics, 2009, 6(5):551−561.

[6] Hanash S M, Pitteri S J, Faca V M. Mining the plasma proteome for cancer biomarkers[J]. Nature, 2008, 452(7178): 571−579.

[7] Sawyers C L. The cancer biomarker problem[J]. Nature, 2008,452(7178): 548−552.

[8] McIntosh M, McIntosh M, Fitzgibbon M. Biomarker validation by targeted mass spectrometry[J]. Nature Biotechnology, 2009,27(7): 622−623.

[9] 厉欣, 徐松云, 张宇, 等. 基于保留时间和质荷比匹配的液相色谱−质谱联用技术用于非标记肽段的差异分析[J]. 分析化学, 2008, 36(7): 867−873.

LI Xin, XU Song-yun, ZHANG Yu, et al. Retention time mass-charge ratio pairs for label-free differential analysis of peptides[J]. Chinese Journal of Analytical Chemistry, 2008,36(7):867−873.

[10] Domon B, Aebersold R. Challenges and opportunities in proteomic data analysis[J]. Molecular & Cellular Proteomics,2006, 5(10): 1921−1926.

[11] Tabb D L, Vega-Montoto L, Rudnick P A, et al. Repeatability and reproducibility in proteomic identifications by liquid chromatography-tandem mass spectrometry[J]. Journal of Proteome Research, 2010, 9(2): 761−776.

[12] Bellew M, Coram M, Fitzgibbon M, et al. A suite of algorithms for the comprehensive analysis of complex protein mixtures using high-resolution LC-MS[J]. Bioinformatics, 2006, 22(15):1902−1909.

[13] Park S K, Venable J D, Xu T, et al. A quantitative analysis software tool for mass spectrometry-based proteomics[J]. Nature Methods, 2008, 5(4): 319−322..

[14] Podwojski K, Fritsch A, Chamrad D C, et al. Retention time alignment algorithms for LC/MS data must consider non-linear shifts[J]. Bioinformatics, 2009, 25(6): 758−764.

[15] Prince J T, Marcotte E M. Chromatographic alignment of ESI-LC-MS proteomics data sets by ordered bijective interpolated warping[J]. Analytical Chemistry, 2006,78(17):6140−6152.

[16] Mueller L N, Brusniak M Y, Mani D R, et al. An assessment of software solutions for the analysis of mass spectrometry based quantitative proteomics data[J]. Journal of Proteome Research,2008, 7(1): 51−61.

[17] Schmidt A, Gehlenborg N, Bodenmiller B, et al. An integrated,directed mass spectrometric approach for in-depth characterization of complex peptide mixtures[J]. Molecular &Cellular Proteomics, 2008, 7(11): 2138−2150.

[18] LIU Ke-hui, ZHANG Ji-yang, WANG Jing-lan, et al.Relationship between sample loading amount and peptides identification and its effects on quantitative proteomics[J].Analytical Chemistry, 2009, 81(4): 1307−1314.

[19] Cleveland W S. Robust locally weighted regression and smoothing scatterplots[J]. Journal of the American Statistical Association, 1979, 74(368): 829−836.

[20] Alterovitz G, Ramoni M F. Systems bioinformatics: an engineering case-based approach[M]. Norwood: Artech House,2007: 112−116.

[21] Benton H P, Wong D M, Trauger S A, et al. XCMS2: processing tandem mass spectrometry data for metabolite identification and structural characterization[J]. Analytical Chemistry, 2008, 80(16):6382−6389.

[22] 林炳昌. 色谱模型理论导引[M]. 北京: 科学出版社, 2004:63−75.

LIN Bing-chang. An introduction of chromatography models[M].Beijing: Science Press, 2004: 63−75.

(编辑 杨幼平)

Reversible retention time alignment algorithm based on local regression

LI Long1, ZHANG Ji-yang1,2, SHI Xiu-jian1, SUN Han-chang1, XIE Hong-wei1, OUYANG Chen-xing3

(1. College of Mechatronic Engineering and Automation, National University of Defense Technology,Changsha 410073, China;2. State Key Laboratory of Proteomics, Beijing Proteome Research Center, Beijing 102206, China;3. School of Business, Central South University, Changsha 410083, China)

A nonlinear and reversible algorithm based on local regression was proposed and implemented, which could reduce the alignment model formn(n−1)/2 ton−1 for anrepeated experiment design. The nonlinear effect of retention time alignment could be modeled by this method, and the negative effect of the peptides with multiple chromatographic peaks could also be overcome. The results show that the time complexity of this algorithm was reduced and the accuracy of it can satisfy the requirement of the following date processing steps.

liquid chromatography-tandem mass spectrometry; quantitative proteomics; retention time alignment; local regression; reversible algorithm

TP391；Q-332

A

1672−7207(2011)01−0100−06

2010−01−10；

2010−09−10

国家自然科学基金资助项目(30621063)

谢红卫(1965−)，男，湖北洪湖人，教授，博士生导师，从事武器装备试验与鉴定技术、复杂系统可靠性分析、人因可靠性分析、生物信息等研究；电话：0731-84576311；E-mail: xhwei65@nudt.edu.cn