结构面强度参数对层状边坡稳定性影响的三维分析

卢敦华，曲艳伟，何忠明，彭文祥，周莲君

(1. 河南工程学院 资源与环境工程系，河南 郑州，451191；2. 长沙理工大学 交通运输工程学院，湖南 长沙，410114；3. 中南大学 地学与环境工程学院，湖南 长沙，410083)

结构面强度参数对层状边坡稳定性影响的三维分析

卢敦华1，曲艳伟1，何忠明2，彭文祥3，周莲君3

(1. 河南工程学院 资源与环境工程系，河南 郑州，451191；2. 长沙理工大学 交通运输工程学院，湖南 长沙，410114；3. 中南大学 地学与环境工程学院，湖南 长沙，410083)

利用FLAC3D数值计算软件建立层状岩体边坡三维计算模型，分析结构面黏结力和内摩擦角变化时边坡安全系数和滑动面的变化规律。研究结果表明：在不同结构面情况下，随着结构黏结力的增大，边坡整体安全系数不断增大，并且两者符合线性关系，此时，边坡滑动面逐渐从临坡面向坡内移动，滑动模式由浅层滑动转换为深层滑动；随着内摩擦角的增大，边坡的安全系数逐渐增大，并且两者符合线性关系，变化滑动面从深部往浅部移动。

结构面；强度参数；层状边坡；稳定性

层状岩体又称板裂岩体，是指分布有一组占绝对优势结构面(如层面、片理面等)的岩体。其优势结构面大多属于物质分异面，所以，层状岩体中构造结构面的稳定情况在很大程度上受控于优势结构面的发育与分布，平行于优势结构面的方向，岩体的组成基本相同，力学性质也基本相同；而垂直于优势结构面的方向，岩体的组成呈现频繁的软硬交替，力学性质相差较大[1−4]。研究结构面强度参数对边坡稳定性的影响具有现实意义。以往一般采用等效模型[5−9]进行研究，如：朱浮声等[5−7]采用等效横观各向同性介质代替真实岩体，对于层状岩体中重要不连续面的性质引入等效模型分析中，并提出一种研究贯通节理岩体等效弹性参数的近似模型，导出了贯通节理岩体基本弹性常数的解析估算公式，编写了相应的较通用的计算程序；张玉军[8]经过坐标变换，得到了在整体坐标系中具有多组任意倾角的节理岩体等效模型。这些研究主要将层状岩体视为均质岩体，而无法反映层状岩体的各向异性特征。为了研究层状岩体的各向异性特征及其数值实现方法，本文首先探讨层状岩体的数值描述方法，然后，研究结构面强度对边坡整体稳定性的影响，以便为工程实践提供参考。

1 计算方法与模型

1.1 计算方法

采用Ubiquitous-Joint模型描述层状岩体，它包含Mohr-Coulomb体内特殊方向上的层理面。层理面的倾向是由笛卡尔坐标分量定义的，在整体坐标中用x，y和z表示，在局部坐标中用x′，y′和z′表示。层理面材料破坏包含拉伸破坏和剪切破坏，破坏包络线由剪切破坏准则fs=0定义：

拉伸破坏修正后的应力增量关系可表示为：

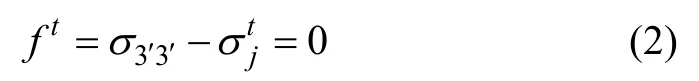
式中：j，cj和分别为层理面的内摩擦角、黏结力和抗拉强度；σ3′3′为层理面上的正应力。

用隐函数gt和gs表征材料的剪切和拉伸塑性流动规律，其中，函数gs对应非关联流动法则：

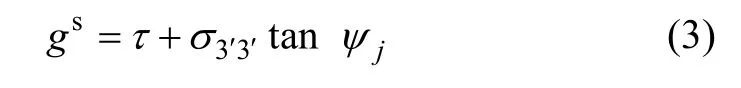
式中：ψj为层理面膨胀角。

函数gt为相关联的流动法则，其形式为：

当岩体应力状态处于稳定区域时，岩体呈弹性状态，不需要进行塑性修正，而进入屈服区域时，根据关联(非关联)流动法则，需进行修正。

1.2 强度折减法的实现

采用强度折减法计算边坡安全系数，其定义为：对材料的强度参数进行折减，直到边坡失稳为止，此时，对应的折减系数即为边坡的安全系数。目前，强度折减法主要应用于Mohr-Coulomb准则[10−14]，本文将进一步推广其在Ubiquitous-joint准则中的应用。由于 Ubiquitous-joint 模型中材料强度参数包括了岩石的黏结力cr、内摩擦角φr以及层理面cj的黏结力和内摩擦角φj，根据应力状态、层理面产状以及模型体和层理面的材料特性的不同，屈服可能发生在岩体内，或者发生在层理面上，或者在2个部分同时发生，因此，在强度折减法实施过程中，同时对cr，tan(φr)，cj和 tan(φj)进行折减。目前，强度折减判断临界状态的标准主要有3个：塑性区判据、位移突变判据和计算不收敛判据，而通过文献[10]中的分析和讨论，可知计算不收敛与位移突变判据的精度最高，而且计算不收敛较易于编程实现。为此，本文利用自编的 FSIH程序判断收敛状态并记录相应安全系数，计算收敛准则为不平衡力比率[15](节点平均内力与最大不平衡力的比值)满足10−5的求解要求。

1.3 数值模型

模型长为275 m，高为133 m，宽为100 m，边坡高为65 m，具体计算模型如图1所示。本构模型采用Ubiquitous- joint准则，初始应力场按自重应力考虑；底部约束3个方向的位移，而侧面主要约束水平位移。岩层自上而下分别为：强风化泥灰岩、微风化泥灰岩和微风化灰页岩。计算参数如表1所示。

图1 计算模型Fig.1 Calculation model

表1 计算参数Table 1 Calculation parameters

2 结果与讨论

2.1 结构面黏结力的影响

由于结构面影响岩体的稳定性，因此，本文主要探讨结构面强度参数的变化对安全系数的影响。图 2所示为不同结构面倾角下结构面黏结力与安全系数的关系，其中结构面倾角变化范围为[30°, 150°]，变化梯度为 30°，结构面倾角与边坡倾向一致，为严格定义的层状边坡；黏结力变化范围为[4, 48] kPa，变化梯度为4 kPa。从图2可以看出：对于不同结构面，随着结构黏结力的增大，边坡整体安全系数不断增大，并且二者符合线性关系，拟合结果见表2。从表2可以看出：当结构面倾角为 90°时，曲线的斜率b最大，为0.005 79，说明边坡对于结构面黏结力的敏感度最强，此时，边坡为直立边坡，其破坏形式主要是层间的拉裂；当结构面倾角从30°变化至60°时，曲线的斜率逐渐减小，说明随着结构面倾角的增大，黏结力发挥的抵抗边坡失稳的作用越来越小；当结构面倾角为150°时，曲线的斜率基本接近于 0，说明结构面黏结力的变化对稳定性的影响很小。

图2 不同结构面倾角下结构面黏结力与安全系数F的关系Fig.2 Relationship between structure plane cohesion and slope safety factor under different structure plane inclinations

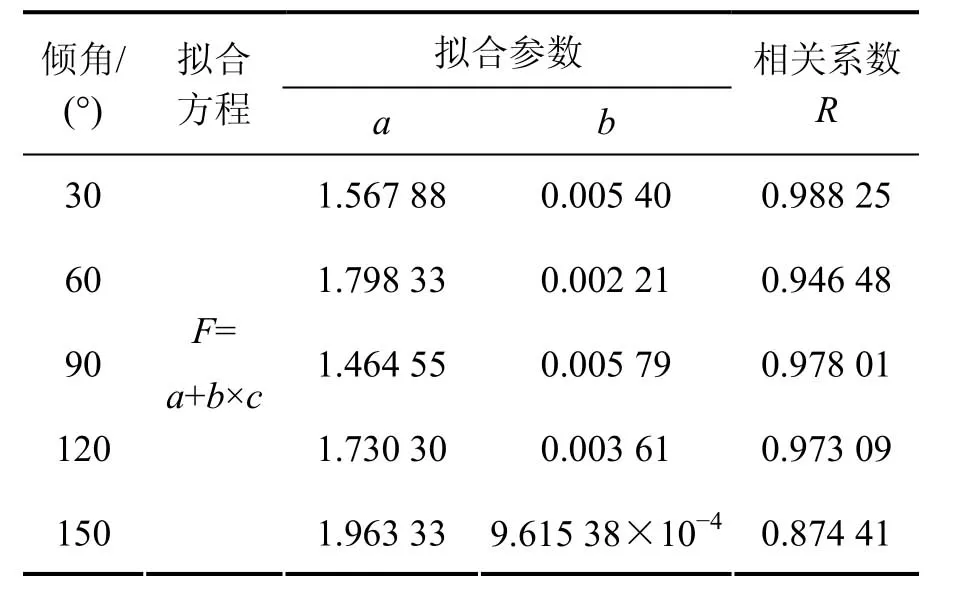
表2 黏结力与安全系数关系的拟合结果Table 2 Fitting results for relationship between structure plane cohesion and slope safety factor

2.2 结构面内摩擦角的影响

图3所示为不同结构面倾角下结构面内摩擦角与边坡安全系数的关系，其中内摩擦角变化范围为[12°, 28°]。从图3可以看出：其变化趋势与图2的趋势相同，随着内摩擦角的增大，边坡的安全系数逐渐增大，并且二者符合线性关系。二者拟合结果见表3。从表 3可以看出：各拟合结果的相关系数R均大于0.950 00，验证了拟合的可靠性；各曲线的斜率均明显大于图2中曲线的斜率，说明内摩擦角对层状岩质边坡稳定性的影响大于黏结力对边坡稳定性的影响；另外，当结构面倾角为90°时，曲线的斜率b最大，结合黏结力的情况，对于直立边坡，其稳定性收到结构面的影响较其他结构面倾角的边坡大。

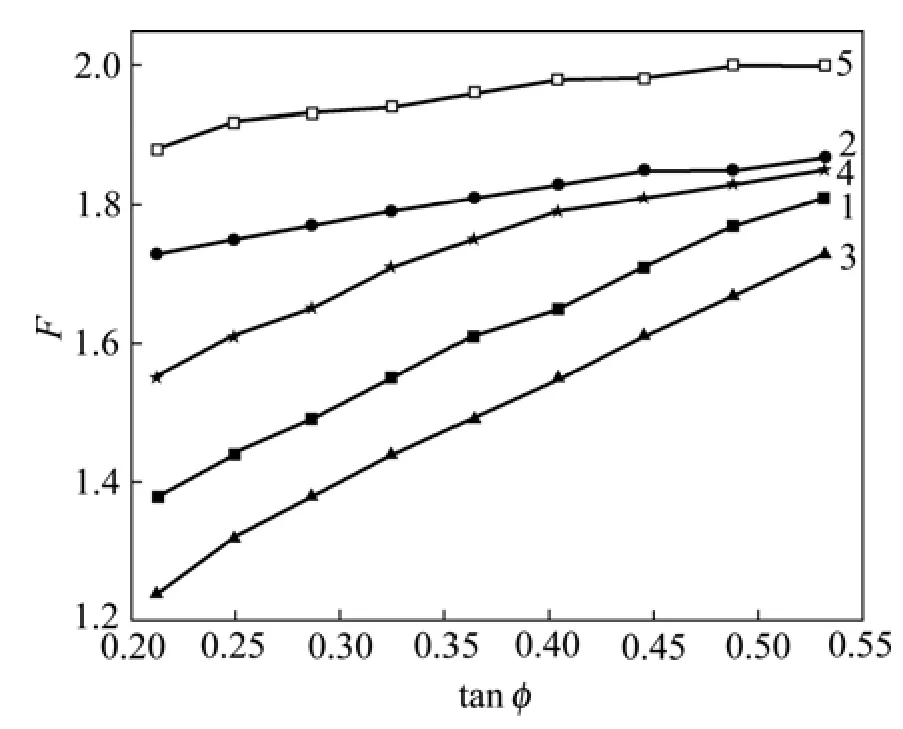
图3 不同结构面倾角下结构面内摩擦角与安全系数F的关系Fig.3 Relationship between structure plane friction angle and slope safety factor under different structure plane inclinations

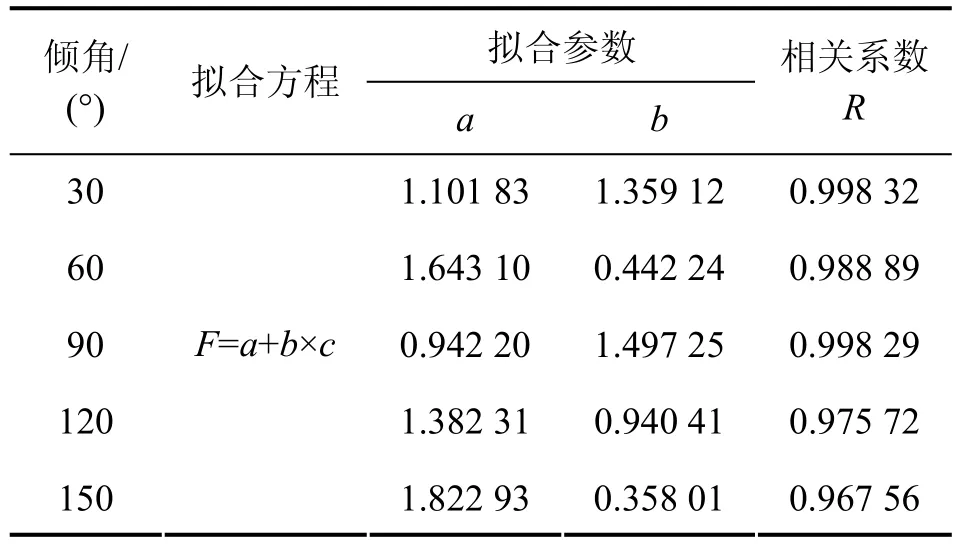
表3 结构面内摩擦角与安全系数关系的拟合结果Table 3 Fitting results for relationship between structure plane friction angle and slope safety factor

2.3 结构面参数变化时的滑动面分析

选取结构面倾角为 60°的边坡进行分析。图 4所示为结构面黏结力变化时边坡滑动面的位置(边坡的位移较塑性区分布情况更能够真实、简便地反映滑动面的位置[10]，因此，本文采用位移云图分布表征边坡的滑动面)。从图4可以看出：随着结构面黏结力的增大，边坡滑动面逐渐从临坡面向坡内移动，滑动模式由浅层滑动转换为深层滑动。图5所示为结构面内摩擦角变化时变化滑动面的位置。从图5可以看出：随着结构面内摩擦角的增大，变化滑动面从深部往浅部移动。

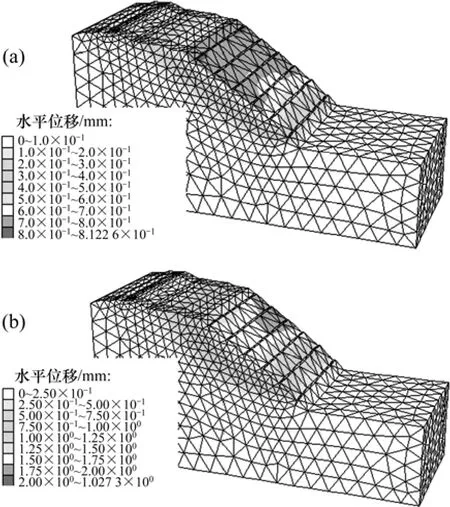
图4 结构面黏结力变化情况下边坡滑动面的变化Fig.4 Variation of slip plane of slope with different structure plane cohesions

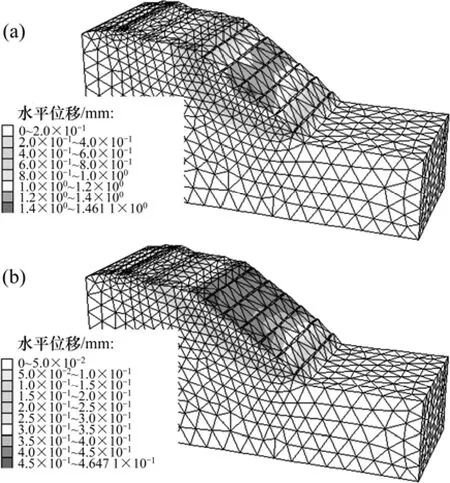
图5 结构面内摩擦角变化时边坡滑动面的变化Fig.5 Variation of slip plane of slope with different structure plane friction angles

3 结论

(1) 对于不同结构面，随着结构黏结力的增大，边坡整体安全系数不断增大，并且二者符合线性关系；随着结构面倾角的增大，黏结力发挥的抵抗边坡失稳的作用变得越来越小；当结构面倾角为 90°时，边坡安全系数对结构面黏结力的敏感度最强。

(2) 随着内摩擦角的增大，边坡的安全系数逐渐增大，并且二者符合线性关系；内摩擦角对层状岩质边坡稳定性的影响大于黏结力对边坡稳定性的影响。

(3) 随着结构面黏结力的增大，边坡滑动面逐渐从临坡面向坡内移动，滑动模式由浅层滑动转换为深层滑动；随着结构面内摩擦角的增大，变化滑动面从深部往浅部移动。

[1] 李银平, 杨春和. 层状盐岩体的三维 Cosserat 介质扩展本构模型[J]. 岩土力学, 2006, 27(4): 509−513.

LI Yin-ping, YANG Chun-he. Three-dimensional expanded Cosserat medium constitutive model for laminated salt rock[J].Rock and Soil Mechanics, 2006, 27(4): 509−513.

[2] 周火明, 盛谦, 陈殊伟, 等. 层状复合岩体变形试验尺寸效应的数值模拟[J]. 岩石力学与工程学报, 2004, 23(2): 289−292.

ZHOU Huo-ming, SHENG Qian, CHEN Shu-wei, et al.Numerical simulation on size-effect in deformation test of layer composite rockmass[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2): 289−292.

[3] 鲜学福. 层状岩体破坏机理[M]. 重庆: 重庆大学出版社,1989: 34−38.

XIAN Xue-fu. Failure mechanism of stratified rock mass[M].Chongqing: Chongqing University Press, 1989: 34−38.

[4] 梁正召, 唐春安, 李厚祥, 等. 单轴压缩下横观各向同性岩石破裂过程的数值模拟[J]. 岩土力学, 2005, 26(1): 57−65.

LIANG Zheng-zhao, TANG Chun-an, LI Hou-xiang, et al. A numerical study on failure process of transversely isotropic rock subjected to uniaxial compression[J]. Rock and Soil Mechanics,2005, 26(1): 57−62.

[5] 朱浮声, 王泳嘉. 层状岩体等效模型数值分析[J]. 东北工学院学报, 1992, 13(6): 530−536.

ZHU Fu-sheng, WANG Yong-jia. Numerical analysis of stratified rock mass by equivalent model[J]. Journal of Northeast University of Technology, 1992, 13(6): 530−536.

[6] 朱浮声. 岩石的强度理论和本构关系[J]. 力学与实践, 1997,19(5): 8−14.

ZHU Fu-sheng. Rock strength theory and its constitutive relationship[J]. Mechanics in Engineering, 1997, 19(5): 8−14.

[7] 晏石林, 黄玉盈, 陈传尧. 贯通节理岩体等效模型与弹性参数确定[J]. 华中科技大学学报, 2001, 29(6): 60−63.

YAN Shi-lin, HUANG Yu-ying, CHEN Chuan-yao. An equivalent model for jointed rock mass with persistent joint and its elastic parameters[J]. Journal of Huazhong University of Science and Technology, 2001, 29(6): 60−63.

[8] 张玉军. 节理岩体等效模型及其数值计算和室内试验[J]. 岩土工程学报, 2006, 28(1): 29−32.

ZHANG Yu-jun. Equivalent model and numerical analysis and laboratory test for jointed rockmasses[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1): 29−32.

[9] 朱浮声, 杜轩, 万明富. 非均质性对岩体应力场反分析结果的影响[J]. 东北大学学报, 2005, 26(10): 1006−1008.

ZHU Fu-sheng, DU Xuan, WAN Ming-fu. Influence of heterogeneity on back analysis results of stress field in rock mass[J]. Journal of Northeastern University, 2005, 26(10):1006−1008.

[10] 林杭, 曹平, 李江腾, 等. 边坡临界失稳状态的判定标准分析[J]. 煤炭学报, 2008, 33(6): 643−647.

LIN Hang, CAO Ping, LI Jiang-teng, et al. Analysis of the standards for critical failure state of slope[J]. Journal of China Coal Society, 2008, 33(6): 643−647.

[11] 栾茂田, 武亚军, 年廷凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报, 2003, 23(3): 1−8.

LUAN Mao-tian, WU Ya-jun, NIAN Ting-kai. A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J]. Journal of Disaster Prevention and Mitigation Engineering, 2003, 23(3): 1−8.

[12] 迟世春, 关立军. 基于强度折减的拉格朗日差分方法分析土坡稳定性[J]. 岩土工程学报, 2004, 26(1): 42−46.

CHI Shi-chun, GUAN Li-jun. Slope stability analysis by lagrangian difference method based on shear strength reduction[J]. Chinese Journal of Geotechnical Engineering, 2004,26(1): 42−46.

[13] LIN Hang, CAO Ping, GONG Feng-qiang, et al. The directly searching method for slip plane and its influential factors based on the critical state of slope[J]. Journal of Central South University of Technology, 2009, 16(1): 131−135.

[14] 宋二祥, 高翔, 邱钥. 基坑土钉支护安全系数的强度参数折减有限元方法[J]. 岩土工程学报, 2005, 27(3): 258−263.

SONG Er-xiang, GAO Xiang, QIU Yue. Finite element calculation for safety factor of soil nailing through reduction of strength parameters[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 258−263.

[15] Itasca Consulting Group. Theory and Background[R]. Minnesota:Itasca Consulting Group, 2002: 76−83.

(编辑 陈灿华)

Three dimensional analysis for effect of structural plane strength parameters on stratified slope stability

LU Dun-hua1, QU Yan-wei1, HE Zhong-ming2, PENG Wen-xiang3, ZHOU Lian-jun3

(1. Department of Resources and Environment Engineering, Henan Institute of Technology, Zhengzhou 451191, China;2. School of Communication and Transportation Engineering, Changsha University of Science and Technology,Changsha 410114, China;3. School of Geoscience and Environment Engineering, Central South University, Changsha 410083, China)

The three dimensional calculation model for stratified rock slope was established by the numerical calculation software FLAC3D, the cohesion and friction angle of structural plane were varied, safety factor and slip plane were analyzed. The results show that, for slope with different inclinations of structural plane, the safety factor of slope increases with the increase of cohesion, and their relationship meets the linear way, while the slip plane moves from the slope surface to the internal of slope, the slipping mode changes from shallow slippage to the deep slippage mode; with the increase of friction angle, the safety factor of slope increases gradually, and their relationship meets the linear way,and the slipping plane moves from internal of slope to the slope surface.

structural plane; strength parameters; stratified slope; stability

TU457

A

1672−7207(2011)01−0147−05

2009−12−01；

2010−03−02

国家自然科学基金资助项目(50878212)；河南工程学院院博士基金资助项目(07089)；河南省基础与前沿技术研究项目(102300410140)

卢敦华(1966−)，男，浙江台州人，副教授，从事地质工程的教学与科研工作；电话：13526565266；E-mail: ldunhua@tom.com