基于单元模态应变能灵敏度的结构损伤统计识别

颜王吉，黄天立，任伟新

(中南大学 土木建筑学院，湖南 长沙，410075)

基于单元模态应变能灵敏度的结构损伤统计识别

颜王吉，黄天立，任伟新

(中南大学 土木建筑学院，湖南 长沙，410075)

基于单元模态应变能灵敏度, 采用概率统计的方法，提出一种同时考虑模型不确定性和测试噪声影响的损伤统计识别方法。首先，建立基于单元模态应变能灵敏度分析的结构损伤方程组，然后，通过摄动法推导出损伤结构刚度参数的统计特性，并运用损伤概率模型计算各单元的损伤存在概率。最后，用一简支梁数值模拟算例验证了该方法的有效性。研究结果表明：损伤概率越大，表明存在损伤的可能性越大；损伤单元的损伤存在概率大于非损伤单元的损伤存在概率；随着损伤程度的增加，损伤存在概率不断增加，而随着噪声水平的增加，损伤存在概率减小。

灵敏度；模态应变能；模态分析；损伤识别；统计方法

基于动力特性的结构损伤识别分析方法的核心问题之一是寻找对结构损伤敏感的损伤参数，由动力参数的变化判断结构损伤情况[1−2]。近年来，模态应变能在机械工程、航天工程和土木工程等领域引起了广泛关注。Lim 等[3−10]等国内外学者都将模态应变能用于结构损伤识别，取得了较满意的结果。目前，基于模态应变能的损伤识别方法以确定性分析方法为主，即根据参数识别结果和相应设计基准值直接对比判别损伤的位置和程度。在工程实际中，测试数据不可避免地要受到噪声、环境因素及运营条件的影响，建模所用的信息也具有不确定性，损伤识别需要考虑这些不确定性因素。尤其是土木工程作为“建造”系统，区别于机械等“制造”系统，不确定因素更多；因此，以确定性方法处理具有本质不确定性的土木工程结构损伤识别问题，导致理论方法与实际应用的矛盾，造成损伤识别结果可靠性差[11]。概率统计理论作为处理不确定性问题的有效工具，将其引入损伤识别可以有效提高识别结果的稳定性和可靠性[12]。相对于确定性损伤识别方法，基于概率统计理论的损伤识别方法能够更好地反映损伤识别问题的不确定性本质。通过将不确定性转化为概率统计意义上的数学表述，从而有效克服其缺陷，是一种比较行之有效的损伤识别方法。本文作者采用概率统计的方法，基于单元模态应变能灵敏度，提出一种同时考虑模型不确定性和测试噪声影响的损伤统计识别方法。首先，建立基于单元模态应变能灵敏度分析的结构损伤方程组；然后，采用摄动法推导出损伤结构刚度参数的统计特性，并运用损伤概率模型计算各单元的损伤存在概率，损伤概率越大，表明存在损伤的可能性越大；最后，用1个简支梁数值模拟算例验证本文方法的有效性，并考虑噪声水平和损伤程度对识别结果的影响。

1 基于单元模态应变能灵敏度的损伤识别

基于代数算法可以推导出单元j对应的r阶模态应变能(Qjr)对任意设计参数(p)的一阶灵敏度表达式[13]：

为了将结构的健康状况描述清楚，需要选取适当的指标，使之既能反映结构的损伤位置，又能反映结构的损伤程度。在有限元层次上，结构单元的损伤可以用各个有限单元的刚度的降低幅度表示(此处用扩阶后的单元刚度矩阵表示)：

由单元模态应变能的灵敏度的代数表达式可以推导出基于单元模态应变能变化的结构损伤方程组[10]：

通过求解该损伤方程组，能够同时识别结构损伤位置和损伤程度，是直接的(不需迭代的)损伤识别方法。然而，求解损伤方程组(3)进行结构损伤识别是一种确定性的方法，没有考虑土木工程中的不确定性，不符合实际工程的需要, 因此，需要引入概率统计方法，使之既能考虑模型的不确定性，又能考虑测试噪声的误差。

2 基于单元模态应变能灵敏度的损伤统计识别

结构整体刚度矩阵和质量矩阵可以表示为：

式中：i和i分别代表损伤前“单元刚度参数”( ESP)和“单元质量参数”(EMP)。以 Euler–Bernoulli梁为例，其ESP为抗弯刚度(EI)，EMP为单位梁长的质量。损伤后的“单元刚度参数”和“单元质量参数”分别用和表示。因此，损伤因子可以表示为：

假设测得的模态参数及系统结构设计参数均为随机变量，它们的误差(这里只考虑偶然误差，不考虑系统误差)服从均值为0的正态分布，且互相独立[14]；因此，损伤结构的振型值、结构物理参数(单元刚度参数和单元质量参数)如下所示：

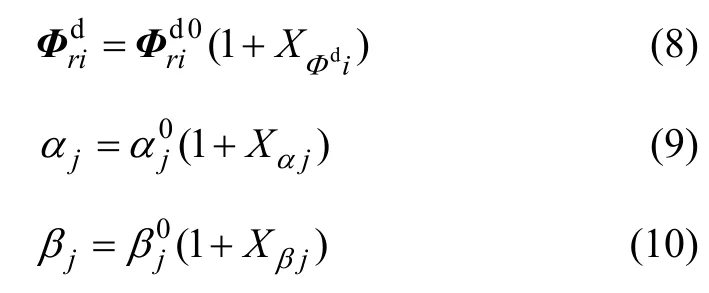
其中：i=1, 2, …,n，n为测试得到的振型矢量元素个数；j=1, 2, …,m(m为结构物理参数数目，此处即单元划分数目)；“0”代表各物理量的均值；，Xαj和Xβj分别为相应物理量的随机噪声。为方便分析，将，Xαj和Xβj合写为新的噪声矢量{X}。由假设可知，E(Xk)=0。

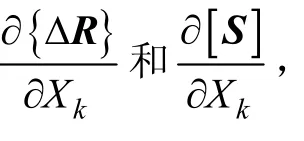
由式(5)，将ΔRjr对噪声Xk求偏导数得:

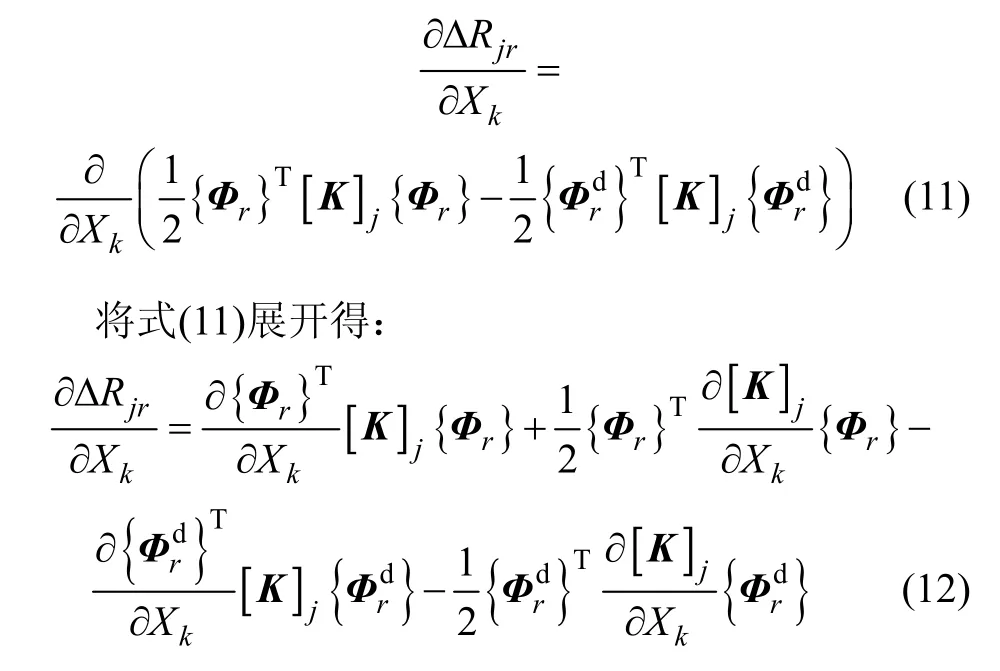
同理，根据式(4)，将Sjir对噪声Xk求偏导数得：

当i≠j时，

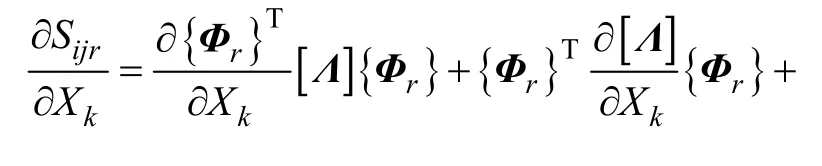
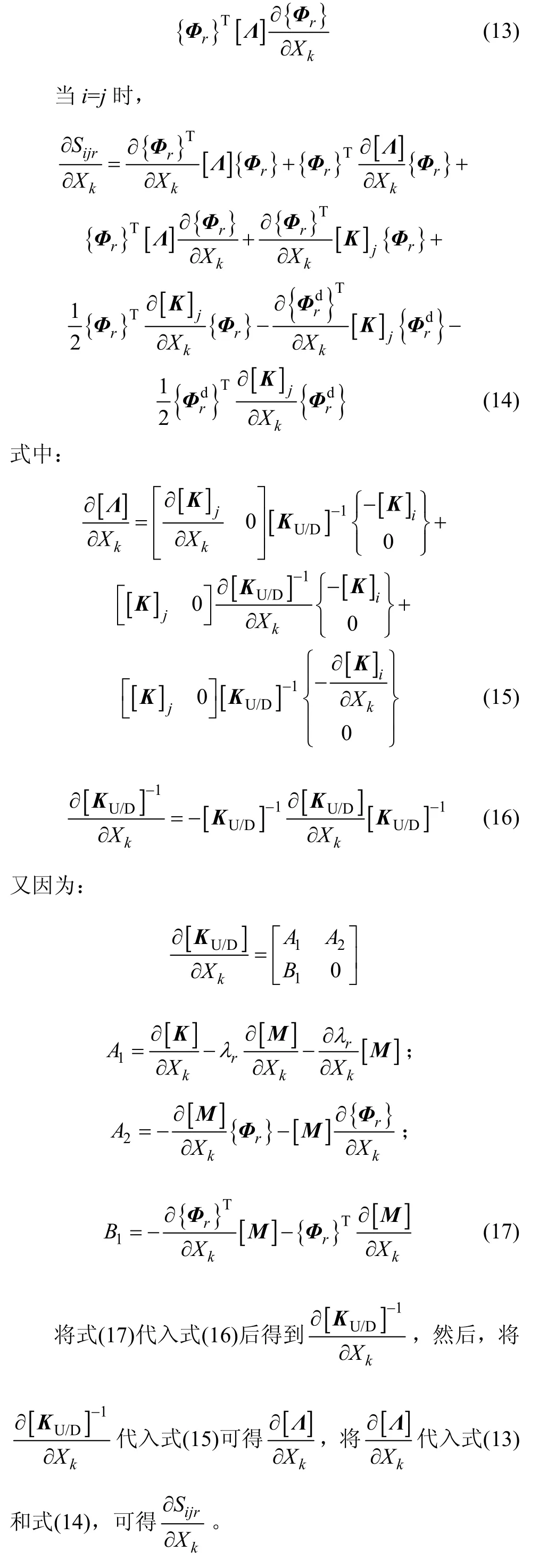
由摄动理论，损伤方程组(3)可以展开为关于噪声向量X的一阶泰勒公式：

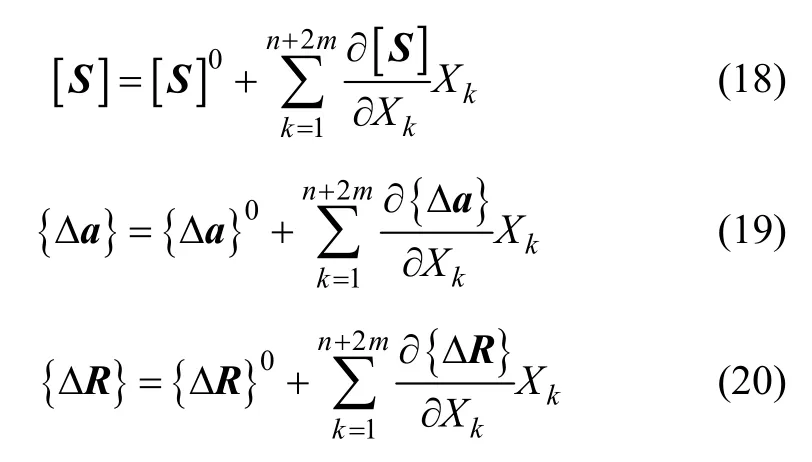
将式(18)～(20)代入损伤方程组(3)，可得：

由于E(Xi)=0，根据式(19), 可得损伤指数的均值为：

式中：下标表示矩阵阶数。

因此，损伤后单元刚度参数的统计特性为：

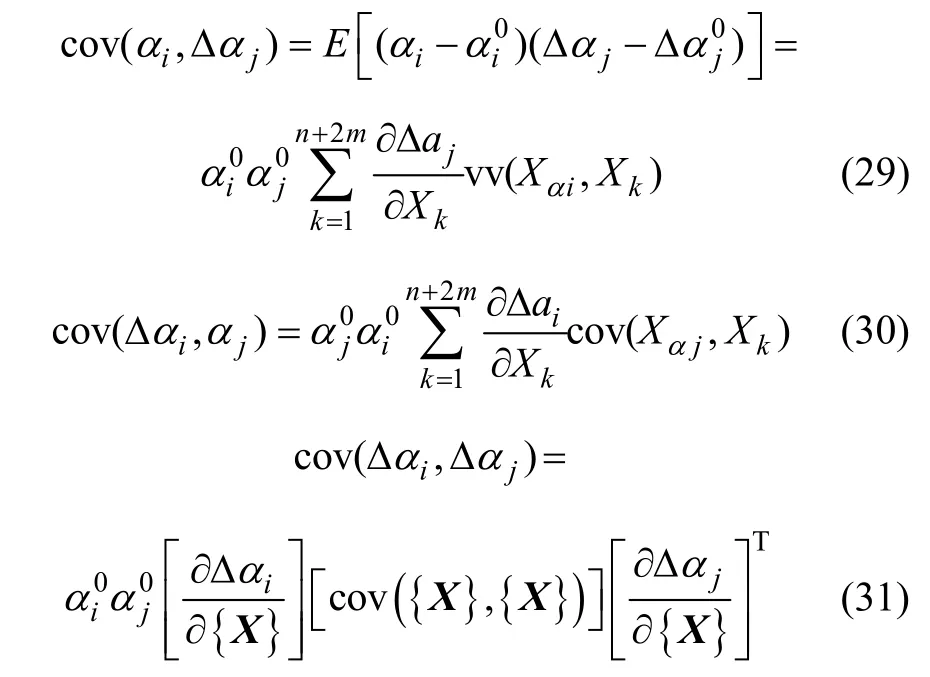
将式(28)～(31)代入式(27)即可得协方差矩阵，这样，由式(26)和(27)可以计算出结构各单元刚度参数的统计特性。需要特别说明的是：由于系数矩阵的列几乎是线性相关的，损伤方程为病态，因而，求逆时，需要先引入奇异值截断算法[15]对系数矩阵进行奇异值截断，保证系数矩阵的数值稳定。

3 损伤的概率判别方法

从结构损伤前后刚度参数的统计分布的变化可以估计出结构的损伤概率[14]，其基本思路是在给定置信度的条件下，在定义的概率密度损伤区间内，计算结构刚度参数的概率。例如，设未损伤时单元的刚度参数服从正态分布 N(E(),σ2())，其概率密度函记为PDF(Probability density function)。结构无损时的刚度参数区间定义为Ω(i,)，其含义是结构在给定的区间内，i的概率为 ，即

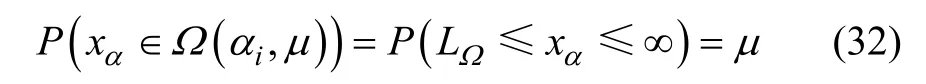
式中：LΩ是给定健康区间的下界； Ω(αi,μ)取决于需要的置信度 ，当 为 95%时，LΩ为E(αi)−1.645σ2(αi)，它意味着无损的结构刚度参数落在 [E(αi)−1.645σ2(αi),∞]中的概率为95%。如果i单元发生损伤，此时其刚度参数服从正态分布N(E() ,σ2())，其单元损伤概率PDE(Probability of damage existence)定义为在 Ω(αi,0.95)以外的概率部分的值，即：

损伤概率取值区间为(μ, 1)，显然，结构损伤概率越接近1，损伤越可能发生；损伤概率越接近0，损伤越不可能发生。

由以上分析可知基于单元模态应变能灵敏度分析的损伤统计识别方法的基本思路为：假设损伤结构参数不确定性和测试噪声均服从正态分布，利用摄动法可以求出损伤结构各单元刚度参数的统计特性(均值和方差)。若已知未损结构和损伤结构刚度参数的概率分布，则根据上面的损伤概率判别方法可以确定结构的损伤存在概率(PDE)，从而达到识别结构损伤的目的。单元的损伤存在概率越大，表明该单元是损伤单元的可能性越大。

4 数值算例

采用的数值试验模型为Euler-Bernoulli梁，如图2所示。梁总长为6 m，划分为10个单元。假设未损结构的几何参数和物理参数(均值)如下：梁的横截面积A为 0.005 m2，惯性矩I=1.67×10−4m4，弹性模量E=32 GPa，容重ρ=2.5 t/m3。

图1 Euler-Bernoulli梁Fig.1 Simulated Euler-Bernoulli beam

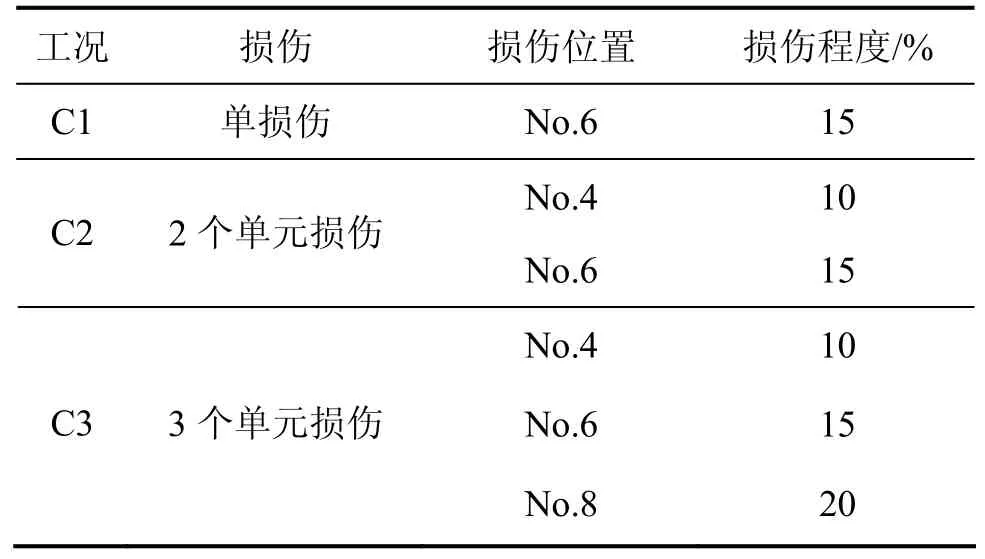
表1 数值试验梁损伤工况Table 1 Simulated damage scenarios

由上面建立的损伤概率判别方法，可以得到每个单元的损伤存在概率，如图2所示。计算结果表明：3种损伤工况的损伤单元的损伤存在概率远大于非损伤单元的损伤存在概率，说明该方法能有效地识别出损伤单元。

图2 各单元损伤存在概率Fig.2 Probability of damage of different elements

为研究不同程度的损伤识别效果，在噪声水平保持不变(1%)前提下，在不同的损伤水平下，前6个单元的损伤存在概率如图3所示。此外，为研究噪声水平的影响，假定噪声水平由1%不断增加为2%，3%，5%和10%，并假设单元3，4，5和6同时发生损伤，且损伤程度均为15%，前6个单元的损伤存在概率如图4所示。

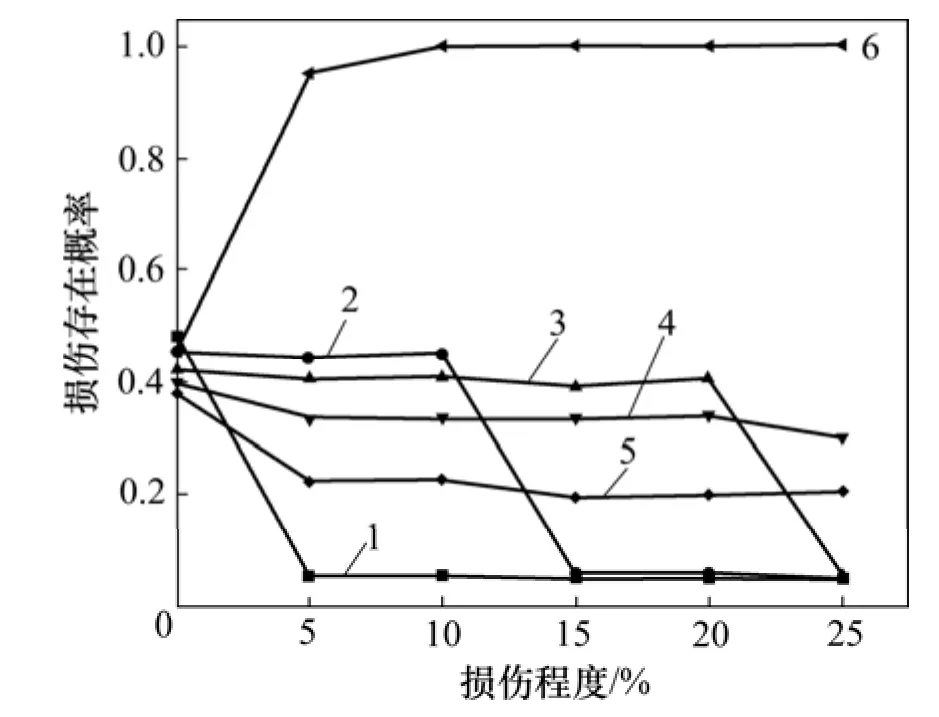
图3 损伤存在概率随损伤程度变化规律Fig.3 Change of PDE with increase of damage level

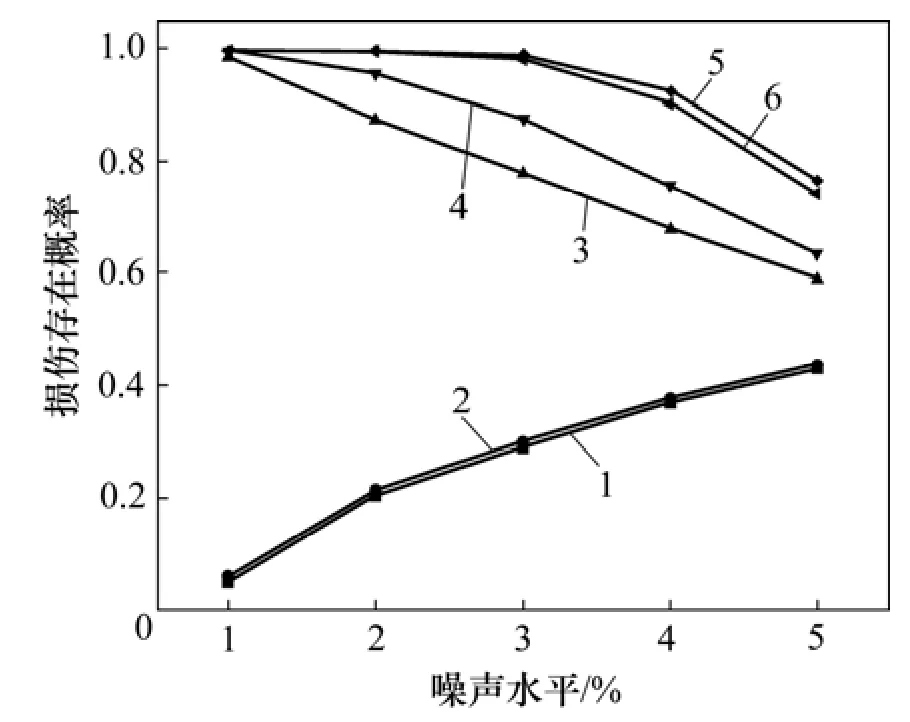
图4 损伤存在概率随噪声水平变化规律Fig.4 Change of PDE with increase of noise level

由图4可见：随着损伤程度的增加，损伤存在概率不断增加，而未损伤单元的存在概率总体上随着损伤程度的增加而减少；随着噪声水平的增加，损伤单元存在概率不断减小，而未损伤单元存在概率总体上随着噪声水平的增加而增加，说明噪声对损伤识别结果有较大的影响。在5种噪声水平下，单元5和单元6的损伤存在概率大于单元3和单元4的损伤存在概率，而且随着噪声增加，单元3和单元4的损伤存在概率下降速率更快；因此，损伤位置对统计识别结果有影响，靠近支座位置损伤比远离支座损伤更难识别，损伤识别结果的准确度和置信度与损伤程度、噪声水平有关。在噪声水平不太大时，本文方法能识别损伤位置。

5 结论

(1) 建立了基于单元模态应变能灵敏度的结构损伤方程组，通过摄动法推导了损伤结构刚度参数的统计特性，然后，运用损伤概率模型计算各单元的损伤存在概率。表达式简洁紧凑，充分利用了矩阵运算的优点，便于编程，便于存储，适用于分析工程领域的大型结构(刚度矩阵和质量矩阵的维数很大)。此外，该方法仅需较少的模态信息，甚至一阶模态信息就足够，没有模态截断引起计算误差的问题。

(2) 损伤单元损伤存在概率远大于非损伤单元的损伤存在概率, 能有效地识别出损伤单元；损伤识别结果的准确度和置信度与损伤程度、噪声水平和损伤位置有关；当噪声水平不是太大时，可以识别损伤位置。随着损伤程度的增加，损伤存在概率不断增加，而未损单元的损伤存在概率总体上随着损伤程度的增加而减少。

[1] Ren W X, De roeck G. Structural damage identification using modal data (Ⅰ): Simulation verification[J]. Journal of Structural Engineering, ASCE, 2002, 128(1): 87−95.

[2] Ren W X, De roeck G. Structural damage identification using modal data (Ⅱ): Test verification[J]. Journal of Structural Engineering, ASCE, 2002, 128(1): 96−104.

[3] Lim T W, Kashangaki T A L. Structural damage detection of space truss structures using best achievable eigenvectors[J].AIAA Journal, 1994, 32(5): 1049−1057.

[4] Stubbs N, Kim J T. Damage localization in structures without base-line modal parameters[J]. AIAA Journal, 1996, 34(8):1644−1649.

[5] Cornwell P, Doebling S W, Farrar C R. Application of the strain energy damage detection method to plate-like structures[J].Journal of Sound and Vibration, 1999, 224(2): 359−374.

[6] Farrar C R, Jauregui D A. Comparative study of damage identification algorithms applied to a bridge (Ⅰ): Experiment[J].Smart Materials and Structures, 1998, 7: 704−719.

[7] Farrar C R, Jauregui D A. Comparative study of damage identification algorithms applied to a bridge (Ⅱ): Numerical study[J]. Smart Materials and Structures, 1998, 7: 720−731.

[8] Shi Z Y, Law S S. Structural damage localization from modal strain energy change[J]. Journal of Sound and Vibration, 1998,218(5): 825−844.

[9] Jaishi B, Ren W X. Finite element model updating based on eigenvalue and strain energy residuals using multiobjective optimisation technique[J]. Mechanical Systems and Signal Processing, 2007, 21: 2295−2317.

[10] Guan H, Karbhari V M. Improved damage detection method based on element modal strain damage index using sparse measurement[J]. Journal of Sound and Vibration, 2008, 309(3/5):465−494.

[11] Bakhtiari-Nejad F, Rahai A, Esfandiari A. A structural damage detection method using static noisy data[J]. Engineering Structures, 2005, 27(12): 1784−1793.

[12] Yeo I, Shin S, Lee H S. Statistical damage assessment of framed structures from static responses[J]. Journal of Engineering Mechanics, ASCE, 2000, 126(4): 414−421.

[13] 颜王吉. 单元模态应变能灵敏度及其在结构损伤识别中的应用[D]. 长沙: 中南大学土木建筑学院, 2008: 15−21.

YAN Wang-ji. Sensitivity study of element modal strain energy and its application in structural damage detection[D]. Changsha:Central South University. School of Civil Engineering and Architecture, 2008: 15−21.

[14] XIA Yong, HAO Hong. Statistical damage identification of structures with frequency changes[J]. Journal of Sound and Vibration, 2003, 263(4): 853−870.

[15] REN Wei-xin Singular value decomposition based truncation algorithm in solving the structural damage equations[J]. Acta Mechanica Solida Sinica, 2005, 18(2): 181−188.

(编辑 赵俊)

Statistical damage identification of structures based on element modal strain energy sensitivity

YAN Wang-ji, HUANG Tian-li, REN Wei-xin

(School of Civil Engineering and Architecture, Central South University, Changsha 410075, China)

A statistical damage identification algorithm based on element modal strain energy sensitivity was developed to account for uncertainties existing in the structural model and measured vibration data. Firstly, an element modal strain energy-based damage detection method was proposed for detecting damage location and severity. Then the statistics of the structural stiffness parameters in the damaged state were estimated by the perturbation method. The probability of damage existence was estimated based on the probability density functions of the structural stiffness parameters in the intact state and damaged state. The presented technique was applied to detect damages in a numerical simply-supported beam. The results show that a higher probability statistically implies a more likelihood of damage occurrence. The probability of damage unit is larger than that of non-damage unit; and the probability increases with the increase of damage level while it decreases with the increase of noise level.

sensitivity; modal strain energy; modal analysis; damage detection; statistical method

TU311.3

A

1672−7207(2011)01−0152−06

2010−01−10；

2010−04−20

国家自然科学基金资助项目(51078357，50708113)；国家“863”计划项目(2009AA11Z101)；中国博士后基金资助项目(2008043152)

黄天立(1977−)，男，湖南长沙人，博士后，从事桥梁结构系统识别及健康监测研究；电话：13787150846；E-mail: htianli@mail.csu.edu.cn