基于遗传算法和神经网络的隧道围岩位移智能反分析
黄戡,刘宝琛,彭建国,冯德山,丁国华,王跃飞
(1. 中南大学 土木建筑学院,湖南 长沙,410075;2. 湖南省交通规划勘察设计院,湖南 长沙,410008;3. 中南大学 地球科学与信息物理学院,湖南 长沙,410075)
基于遗传算法和神经网络的隧道围岩位移智能反分析
黄戡1,2,刘宝琛1,彭建国2,冯德山3,丁国华2,王跃飞2
(1. 中南大学 土木建筑学院,湖南 长沙,410075;2. 湖南省交通规划勘察设计院,湖南 长沙,410008;3. 中南大学 地球科学与信息物理学院,湖南 长沙,410075)
基于正交试验设计和FLAC3D建立的学习样本以及测试样本,通过工程现场获取的围岩位移信息,用神经网络建立待反演参数与围岩位移之间潜在的映射关系。研究结果表明:利用该神经网络的仿真预测功能,结合遗传算法搜索反演参数的最优解,从而实现位移反分析;可将反演结果反馈于隧道支护结构的设计,实现隧道的信息化施工与设计。
位移反分析;遗传算法;神经网络;正交试验
在进行岩体工程设计和施工时,人们为了得到岩体的原始地应力场和围岩力学参数,为得到这些参数,人们提出了位移反分析法。位移反分析法就是根据隧道开挖引起的周边位移来反演地下工程设计所需参数的一种计算方法。随着有限元等数值计算的发展和隧道施工中对监控量测的重视,位移反分析法逐步得到发展并取得了令人瞩目的成果[1−3]。在此,本文作者结合遗传算法和神经网络对公路隧道围岩位移智能反分析方法的研究建立一个可靠、实用、易于推广的位移反分析方法。用施工过程中,监控量测得到的围岩位移信息(如拱顶下沉、洞周收敛位移)进行反分析,得到初始地应力参数以及岩体的力学参数,将其反馈于隧道支护结构的设计,以便实现隧道的信息化施工与设计[4]。
1 隧道围岩位移反演参数的确定
影响位移反分析准确性的一个重要因素是介质模型的选择。选择的模型不同,位移反分析的结果会大不相同。选择模型时考虑的因素越多,模型就越接近隧道围岩的真实力学模型,需要反演的参数也就越多,位移反分析过程中遇到的困难也越大,这样,就产生了介质模型的选择与位移反分析准确性之间的矛盾。其实,隧道围岩是一种非均质、不连续、非线性和流变的材料,要选择的模型与实际情况相吻合,这几乎是不可能的,也没有必要。从工程实用的角度出发,在位移反分析时采用的模型宜简单,材料的本构模型参数宜适宜[5]。
1.1 隧道围岩物理力学反演参数
岩体力学特性参数主要有变形性质参数与强度特性参数。由于岩体的非均质、不连续与监测点位置的局限性,现场应力(应变)测试难度大,量测值离散性也大,很难应用于判定岩体的稳定性;而岩体变形(位移)较易量测,较易与岩体的稳定性经验判据建立联系,因此,待反演的参数通常取变形性质参数。而岩体的强度特性参数中的内摩擦角和黏聚力较容易通过现场和试验室的试验得到,故不把强度参数作为反演参数,而作为已知参数。岩体变形性质参数主要有 2个,即变形模量和泊松比。由于地层中的泊松比变化幅度较小,对围岩变形的影响比变形模量的影响小,因此,计算模型中将泊松比作为已知输入。但是,隧道围岩的变形模量不易通过试验得到,试验得到的变形模量通常也是岩石的变形模量,而不是围岩(岩体)的变形模量,这与实际情况有很大差别[6]。为此,本文作者将变形模量作为围岩位移智能反分析系统的反演参数之一。
1.2 隧道围岩初始地应力反演参数
处于复杂地质条件下的大型隧道工程将受到天然形成的地质环境(如应力场、渗流场、岩体物理力学性质等因素)的制约与影响。通过工程实践,人们认识到岩体中的初始应力场是地下工程围岩稳定与支护结构设计所需要的基本资料之一,因此,采用的初始地应力场是否可靠,岩体参数选取是否合理,将直接影响到工程设计与施工是否可靠与安全。虽然现场实测地应力提供地应力场是最直接的途径,但在工程现场,由于场地和经费等原因,不可能进行大量测量。而且地应力场成因复杂,影响因素多,各测点测量成果在很大程度上反映了当地的局部应力场,且测量结果受测量的影响,使得地应力测量成果有一定程度的离散性;因此,必须对初始地应力场进行分析计算,以获得更准确的、适用范围较大的初始地应力场[7]。
本文将初始地应力场分为垂直地应力场σv和水平地应力场σh,并认为垂直地应力等于上覆岩层的重力,而水平地应力场与垂直地应力场有关,即σh=kσv(其中,k为侧压力系数)。在隧道中,任意一点埋深已知,则该处的垂直地应力场已知,而侧压力系数与该点所处的地质环境有关,视具体情况而定;因此,这里将地应力侧压力系数k作为反演参数。
2 智能位移反分析法操作步骤
公路隧道围岩位移智能反分析法的基本思路是:通过工程现场获取的围岩位移,基于FLAC3D建立的学习样本以及测试样本,用神经网络建立待反演参数与围岩位移之间潜在的映射关系,然后,利用该神经网络的仿真预测功能,结合遗传算法搜索反演参数的最优解,从而实现位移反分析,以达到在现场取得可信的位移后,可以进行快速位移反分析,得到支护结构设计中所需参数。
2.1 采用遗传算法优化神经网络结构
不同的神经网络结构对模型的学习和推广预测能力有直接影响。对于大多数实际问题,采用一层中间层即三层网络就足够了,但当采用1个中间层时,需要用较多的处理单元;若选用2个中间层,则每层处理单元会大大减少且能取得较好的效果。对于中间层单元数,若选用太少,则网络难以处理较复杂的问题;但若中间层处理单元数过多,不仅会使网络训练时间急剧增加,而且容易使网络训练过度。另外,BP网络的收敛过程存在一个很大的缺陷,即“局部最小值”问题。在学习过程中,有时会发现当学习反复进行到一定次数后,虽然网络的实际输出与希望输出还存在很大的误差,但无论怎样学习,网络全局误差的减小都变得非常缓慢或者根本不再变化,这种现象是网络收敛于局部最小值所致。适当改变 BP网络中间层的单元数可使收敛避开局部极小值点;因此,构造一个令人满意的神经网络模型是至关重要的[8−10]。
应用遗传算法可以搜索到最佳的神经网络结构。由于网络的输入层节点数和输出节点数由问题的特征而定,故只需要搜索网络隐含层数和隐含层点数。常用的网络层有3~4层,采用的隐含层越多,训练时间就会急剧增加;另外,隐含层增加后,局部最小误差也会增加,网络在训练过程中容易陷入局部最小误差,网络的权重难以调整到最小误差处[11−13]。因此,本文应用遗传算法在2层的隐含层中搜索最佳的隐含层单元数。智能位移反分析法操作步骤为:
(1) 确定决策变量及其各种约束条件,决策变量为中间层单元数。
(2) 定义遗传算法中的目标函数。
(3) 确定表示可行解的染色体编码方法和解码方法。
(4) 确定目标函数值f(X)到个体适应度F(X)的转换规则。
(5) 输入遗传算法的有关运行参数。
(6) 输入神经网络的输入节点数NI(即待反分析参数的数目)、输出层节点数NO(即已知位移个数)。
(7) 将学习样本进行规范化,即将学习样本中的输入、输出数据转换到[0,1]或[−1,1]区间。
(8) 输入神经网络学习样本。
(9) 输入神经网络最多学习次数和全局误差的判别值。
(10) 设置进化代数计数器t=0,随机生成N个个体作为初始群体p(0),群体中的个体用二进制编码表示,每个个体代表1个网络结构。
(11) 将群体p(t)中的个体解码成十进制表示。
(12) 给每个个体(即每一种网络模型)的各连接权和阀值赋予[−1, +1]间的随机值。
(13) 随机选取1个样本提供给每个网络。
(14) 按照 BP神经网络的算法对群体p(t)中的每个神经网络进行训练,并计算全局误差E。
(15) 若全局误差E小于预先设定的值,则停止计算并输出搜索到的网络结构;否则,进行下一轮网络训练。
(16) 若学习次数大于预先设定的值且全局误差都不小于预先设定的值,则根据目标函数值(即全局误差)到个体适应度F(X)的转换规则计算各个个体(即各个神经网络)的适应度。
(17) 对群体p(t)进行选择运算、交叉运算和变异运算等遗传操作,得到下一代群体p(t+1)。
(18) 终止条件判断。若t≤T,则t←t+1,转到步骤(9);若t>T,则以进化过程中得到的具有最大适应度的个体作为最优解输出,终止计算。
2.2 采用遗传算法进行参数反分析
采用神经网络建立岩体力学参数、初始地应力侧压力系数与岩体位移之间的映射关系之后,对于任意给定的岩体力学参数,可以通过网络的推广预测能力求出其相应的位移;因此,可以在给定岩体力学参数与初始地应力系数取值范围的基础上,应用遗传算法结合神经网络对参数进行搜索寻优。这样,将遗传算法和神经网络结合应用于位移反分析,既利用了神经网络的非线性映射、网络推理和预测功能,又利用了遗传算法全局优化特性,在处理变量与目标函数值之间无明显的数学表达式的复杂工程问题中,具有较高的应用价值[14−16]。
综合以上分析,可以得出应用神经网络和遗传算法进行位移反分析的步骤如下。
(1) 确定目标函数。本文采用的目标函数为最小二乘目标函数,即
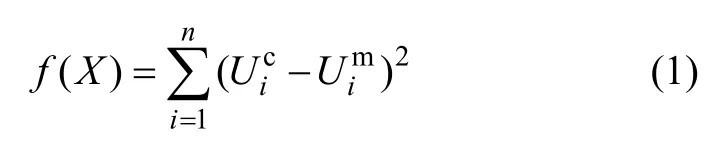
式中:n为测点个数;为第i个测点的计算位移,由训练好的神经网络预测得到;为第i个测点的实际位移,由现场的监控量测得到。
(2) 通过正交试验方法设计试验方案,通过FLAC3D有限元计算获取训练样本。
(3) 通过神经网络对步骤(2)建立的训练样本进行学习,搜索到最佳的神经网络结构,从而建立了输入与输出之间的非线性映射关系。
(4) 采用均匀设计法构造神经网络测试样本,测试神经网络预测能力。
(5) 对进化神经网络模型进行初始化设置,确定待反分析的岩体力学参数取值范围。
(6) 在待反分析参数的取值范围内,随机地产生一组可能的取值。参数的每个取值是1个二进制代码表示的染色体。
(7) 将参数的每一取值输入已经训练好的神经网络模型,预测其位移并计算位移的预测误差(适应度)。
(8) 若适应度满足精度要求,则认为找到了最优解,停止计算并输出参数值和预测位移;若适应度不满足要求,则进行参数取值染色体的遗传进化操作,对每一参数取值的染色体进行复制、杂交、变异等遗传操作,产生一子代可能的参数取值群体。
(9) 重复进行步骤(7)和(8),直至找到最合理的参数值为止。
3 雪峰山隧道Ⅳ级围岩位移智能反分析
以雪峰山隧道Ⅳ级围岩地区为例,系统介绍隧道围岩位移反分析法的应用。由于YK99+750 m断面附近的工程地质条件,隧道的施工方法和初期支护措施等方面在整个隧道Ⅲ类围岩地区具有代表性,因此,通过对YK99+730~755 m进行FLAC3D数值模拟,以获取神经网络的训练样本。
3.1 计算模型
采用FLAC3D建立隧道模型进行正交试验和均匀试验,对里程YK99+730~755 m研究段进行开挖支护模拟。本模型的计算长度沿隧道轴线方向取25 m,计算宽度以隧道设计中线向左、右各延伸40 m,竖直方向上、下各延伸35 m。由于隧道距地表约725 m,属于深埋隧道,为了方便,不考虑地表具体地形地貌,将模型顶面近似为平面。本文模型的边界为四周和底面约束法向位移,顶面为自由表面。这里的地应力场近似看作自重应力场,因此,在几何模型平面上施加上覆岩体重力,且水平应力等于自重应力与侧压力系数的乘积。
在FLAC3D计算模型中,围岩采用实体单元进行模拟,且采用莫尔−库仑(Mohr-Coulomb)准则作为塑性屈服准则。考虑到计算时间,隧道初期支护的喷射混凝土采用实体单元并以弹性模型进行模拟;同时,初期支护中的系统锚杆采用 cable锚索单元进行模拟。FLAC3D建立的模型如图1所示,共生成21 322个节点,18 824个单元。
3.2 施工过程的模拟
由于在本文建立的隧道围岩位移反分析研究中,需要建立围岩力学参数及初始地应力参数与围岩位移的关系作为神经网络的训练样本;同时,为了通过数值模拟计算得到的位移,本文在隧道模拟开挖的过程中,在隧道断面布设3个监测点(如图2(a)所示),分别监测隧道拱顶及边墙位移。

图2 隧道开挖示意图Fig.2 Diagraph of excavation
根据勘察报告可知:YK99+730~755 m属于Ⅳ级围岩,地质条件较好,施工单位采用钻爆法进行全端面开挖,每循环进尺5 m左右,其开挖示意图如图2(b)所示。FLAC3D模拟开挖过程计算步骤如下。
第1步:计算模型在自重应力作用下达到平衡,将全部节点位移置为0。
第2步:开挖YK99+750~755 m路段,即第Ⅰ部分围岩;同时,在YK99+750端面处设置点1,2和3共3个监测点,计算平衡模型,监测拱顶及边墙位移情况。
第3步:在YK99+750~755 m段内施工系统锚杆、喷射混凝土等初期支护结构,计算平衡模型以及监测点1,2和3点在初期支护结构作用下的围岩位移。
第4步:考虑空间效应,将掌子面向前开挖5 m,即开挖第Ⅱ部分围岩,计算平衡模型以及监测点1,2和3的位移。
第5步:开挖YK99+740~745 m段,即第Ⅲ部分围岩,同时,在第Ⅱ部分围岩段开挖施工系统锚杆、喷射混凝土。
第6步:计算平衡模型,使模型达到平衡状态,此时,点1,2和3这3个监测点的位移就是本文研究所需要的位移,用于构造神经网络的学习样本和检验样本。
3.3 样本的构造
3.3.1 参数水平
根据资料,可以确定弹性模量E为5~8 GPa,侧压力系数K为 0.3~1.5。为了构造神经网络的学习样本,采用正交试验设计方法设计试验方案,其中试验因素为2个参数,即E和K,且每个因素分为5个水平,各参数水平划分见表1。
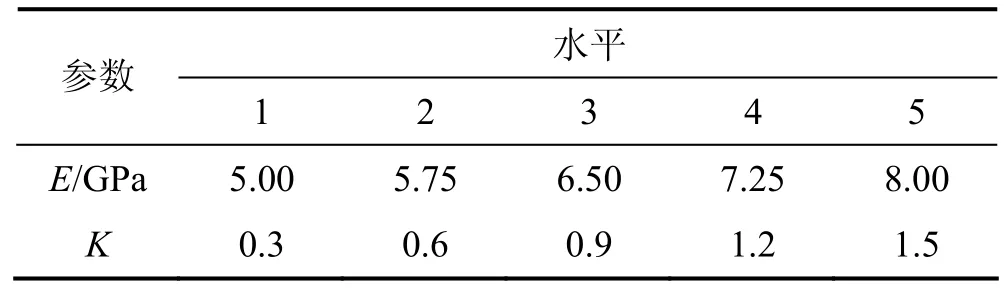
表1 各参数水平划分Table 1 Level division of each parameter
3.3.2 训练样本试验设计
本文研究的试验含有2个试验因素、5个水平。在进行正交试验设计时可采用正交表L25(56),部分实验结果如表2所示。表2中:第1列表示试验编号,第2行表示试验因素,表中间数据则表示试验因素的各水平。
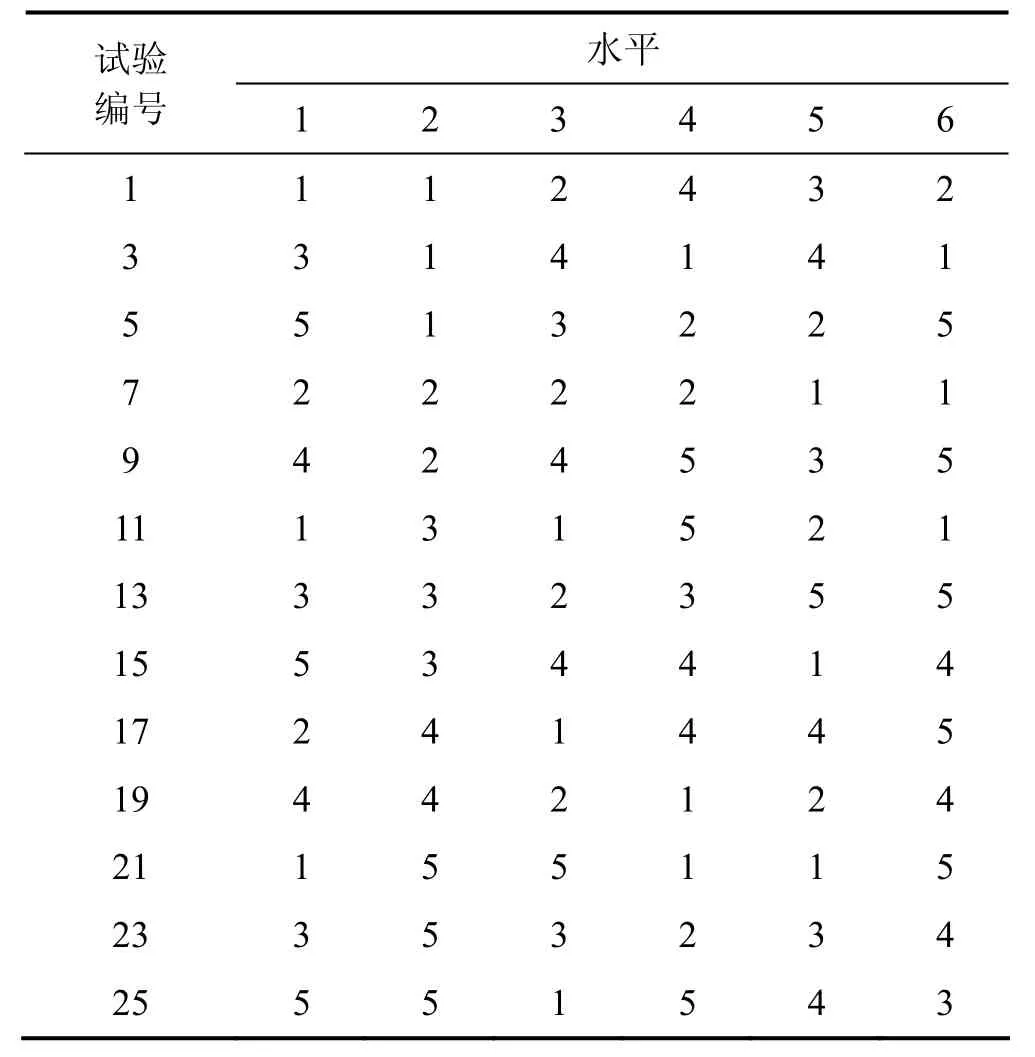
表2 正交试验表Table 2 Orthogonal design test table
3.3.3 训练样本结果
根据正交表L25(56)将各试验因素的水平进行组合得到试验方案,用数值模拟软件FLAC3D计算各试验方案下YK99+750端面点1,2和3的位移,由此得到 25个神经网络的训练样本。部分训练样本如表 3所示。
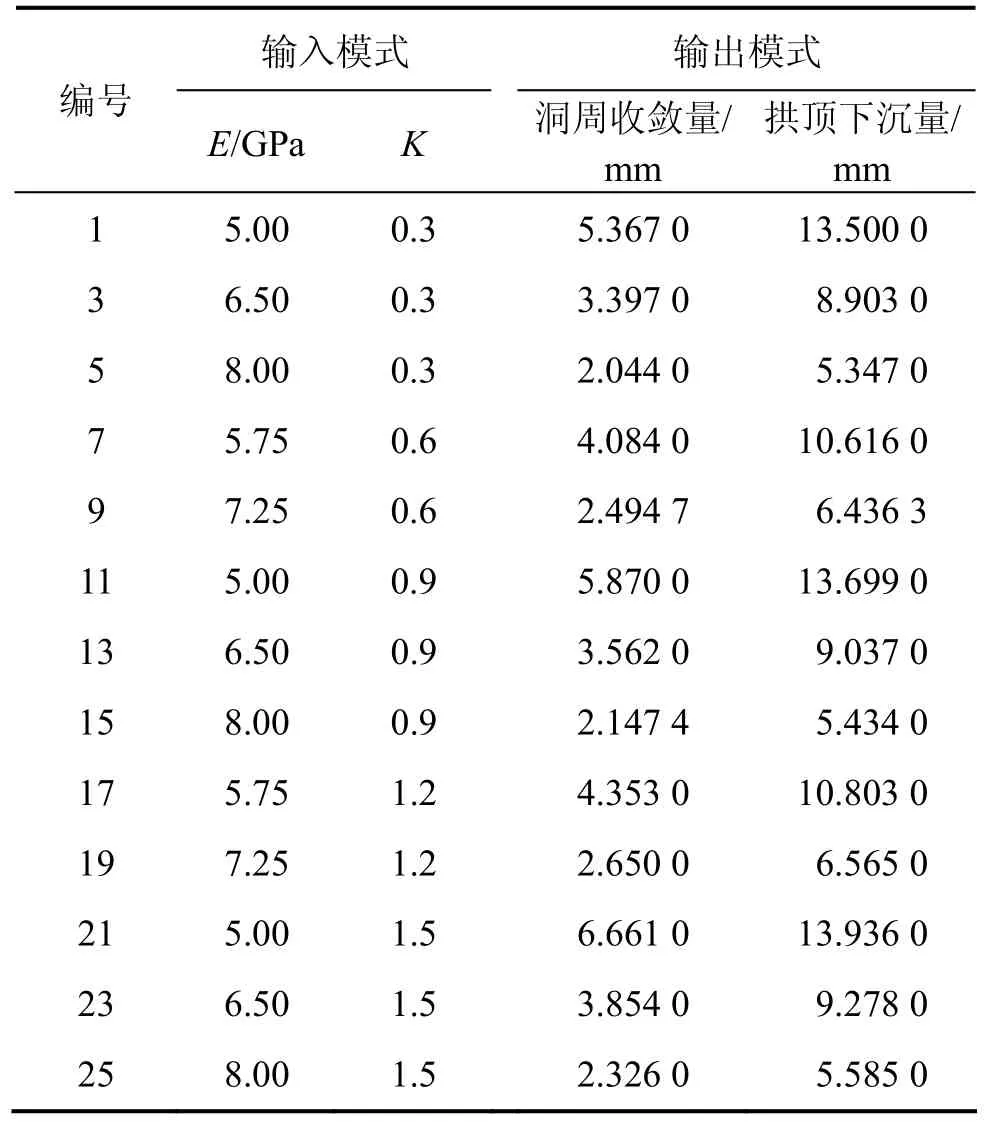
表3 神经网络训练样本Table 3 Neural network training samples
4 结果分析
4.1 神经网络结构搜索结果
用遗传算法搜索神经网络结构2层中间层的单元个数过程中,将每一代遗传操作中目标函数计算结果最小的个体记录下来,其部分结果见表4。由表4可知:最优的神经网络结构为第1中间层单元数为38,第2中间层单元数为42,此时,全局误差为0.001 205。因此,确定本论文中最优的神经网络结构为 2—38—42—2。
4.2 参数反演结果
用遗传算法搜索岩体弹性模量E和初始侧压力系数K的过程中,使目标函数计算结果最小的个体则为参数反分析的最优解,即参数反演结果。参数反演结果见表5。由表5可知:围岩岩体弹性模量E为5.8~8.0 GPa,初始侧压力系数K为0.62~1.50。
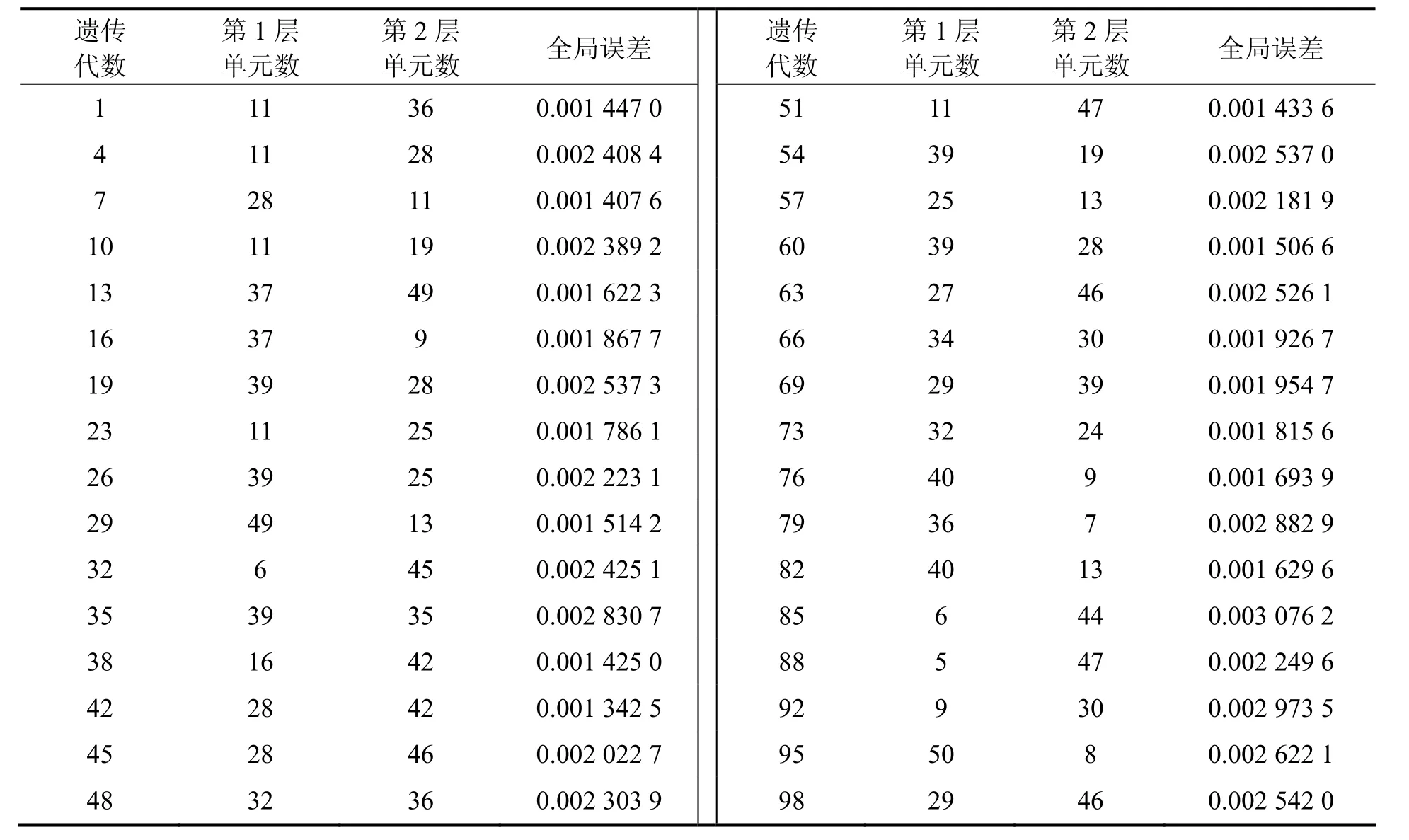
表4 遗传算法搜索神经网络结构结果Table 4 Neural network structure search results by genetic algorithm

表5 参数反分析结果Table 5 Back analysis results
5 结论
(1) 将遗传算法和神经网络结合应用于位移反分析既利用了神经网络的非线性映射、网络推理和预测功能,又利用了遗传算法全局优化特性,从而获得反演参数的最优解。
(2) 为了减小数值模拟工况,应用正交试验设计方法设计试验方案,其中试验因素为2个,即弹性模量E和侧压力系数K,且每个因素分为5个水平。
(3) 针对本工程的算例,其最优的神经网络结构为 2—38—42—2,反演得到围岩岩体弹性模量为5.8~8.0 GPa,初始侧压力系数为0.62~1.50。
[1] 张川, 刘新宇, 侯晓峰. 基于位移反分析的隧道参数模拟研究[J]. 地下空间与工程学报, 2005, 1(3): 379−382.
ZHANG Chuan, LIU Xin-yu, HOU Xiao-feng. Application of the displacement back analysis in the construction of city-highway tunnel[J]. Journal of Underground Space and Engineering, 2005, 1(3): 379−382.
[2] 梅松华, 李文秀, 盛谦. FLAC在岩土工程参数反演中的应用[J]. 矿冶工程, 2000, 20(4): 23−26.
MEI Song-hua, LI Wen-xiu, SHENG Qian. Application of FLAC in back analysis of geotechnical parameters[J]. Mining and Metallurgical Engineering, 2000, 20(4): 23−26.
[3] 易小明, 陈卫忠, 李术才, 等. BP神经网络在分岔隧道位移反分析中的应用[J]. 岩石力学与工程学报, 2006, 25(S2):2411−2419.
YI Xiao-ming, CHEN Wei-zhong, LI Shu-cai, et al. Application of BP neural network to back analysis of forked tunnel displacement[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 2411−2419.
[4] 关宝树. 隧道工程施工要点集[M]. 北京: 人民交通出版社,2003: 28−36.
GUAN Bao-shu. Tunnel construction main points[M]. Beijing:People Transportation Press, 2003: 28−36.
[5] 彭建国, 蒋成海, 吴湘滨, 等. 雪峰山隧道区域地下水影响调查研究[R]. 长沙: 中南大学地学与环境工程学院, 2007:56−61.
PENG Jian-guo, JIANG Cheng-hai, WU Xiang-bin, et al. Study and investigation of groundwater inflection on Xuefeng mountain tunnel excavation[R]. Changsha: Central South University. School of Geology Science and Environmental Engineering, 2007: 56−61.
[6] 杨小礼, 眭志荣. 应力剪胀对浅埋隧道稳定性系数的影响[J].中南大学学报: 自然科学版, 2008, 39(1): 190−195.
YANG Xiao-li, SUI Zhi-rong. Influences of stress dilatancy on stability factors of shallow tunnels[J]. Journal of Central South University: Science and Technology, 2008, 39(1): 190−195.
[7] 易达, 徐明毅, 陈胜宏, 等. 人工神经网络在岩体初始应力场反演中的应用[J]. 岩土力学, 2004, 25(6): 190−195.
YI D, XU Ming-yi, CHEN Sheng-hong, et al. Application of artificial neural network to back analysis of initial stress field of rock masses[J]. Rock and Soil Mechanics, 2004, 25(6):190−195.
[8] 彭建国, 王兰生, 徐进, 等. 雪峰山隧道施工地质勘察技术研究[R]. 长沙: 湖南省交通规划勘察设计院, 2007: 188−193.
PENG Jian-guo, WANG Lan-sheng, XU Jin, et al. Study and construction geology survey on Xuefeng mountain tunnel excavation[R]. Changsha: Hunan Provincial Communication Planning Survey and Design Institute, 2007: 188−193.
[9] 周家文, 杨兴国, 吴震宇, 等. 浅埋岩体隧洞初始地应力场位移反分析方法研究[J]. 四川大学学报: 工程科学版, 2010,9(1): 48−56.
ZHOU Jia-wen, YANG Xing-guo, WU Zhen-yu, et al.Displacement back analysis of initial stresses filed of shallow rock masses tunnel[J]. Journal of Sichuan University:Engineering Science Edition, 2010, 9(6): 48−56.
[10] 刘学增, 苏京伟. 粘弹性动态增量反演分析在隧道施工中的应用[J]. 同济大学学报: 自然科学版, 2009, 37(10): 80−85.
LIU Xue-zeng, SU Jing-wei. Application of viscoelastic staged incremental back analysis in tunnel construction[J]. Journal of Tongji University: Natural Science, 2009, 37(10): 80−85.
[11] 刘开云, 乔春生, 刘保国. 基于遗传-广义回归神经元算法的坞石隧道三维弹塑性位移反分析研究[J]. 岩土力学, 2009,30(6): 180−185.
LIU Kai-yun, QIAO Chun-sheng, LIU Bao-guo. Research on elastoplastic displacement back analysis method based on GA-GRNN algorithm in three-dimension of Wushi tunnel [J].Rock and Soil Mechanics, 2009, 30(6): 180−185.
[12] 马亢, 徐进, 张志龙, 等. 基于二次应力实测值的初始应力场反分析法及其工程应用[J]. 四川大学学报: 工程科学版, 2008,40(6): 51−56.
MA Kang, XU Jin, ZHANG Zhi-long, et al. The back analysis method based on practical secondary-stress value an its application to engineering[J]. Journal of Sichuan University:Engineering Science Edition, 2008, 40(6): 51−56.
[13] 白世伟, 韩昌瑞, 顾义磊, 等. 隧道应力扰动区地应力测试及反演研究[J]. 岩土力学, 2008, 29(11): 2887−2892.
BAI Shi-wei, HAN Chang-rui, GU Yi-lei, et al. Research on crustal stress measurement and inversion of stress disturbed area of a tunnel[J]. Rock and Soil Mechanics, 2008, 29(11):2887−2892.
[14] 王薇, 王连捷, 乔子江, 等. 三维地应力场的有限元模拟及其在隧道设计中的应用[J]. 地球学报, 2004, 25(5): 587−591.
WANG Wei, WANG Lian-jie, QIAO Zi-jiang, et al. Modeling of three dimensional crustal stress fields and its application in tunnel design[J]. Acta Geosicientia Sinica, 2004, 25(5):587−591.
[15] 朱光仪, 郭小红, 陈卫忠, 等. 雪峰山公路隧道地应力场反演及工程应用[J]. 中南公路工程, 2006, 31(1): 71−75.
ZHU Guang-yi, GUO Xiao-hong, CHEN Wei-zhong, et al.Inversion of in situ stress and its application in Xuefengshan roadway tunnel[J]. Journal of Central South Highway Engineering, 2006, 31(1): 71−75.
[16] 靳晓光, 李晓红, 艾吉人, 等. 某深埋长隧道地应力演化及围岩应力位移模拟研究[J]. 水文地质工程地质, 2004(1): 40−43.
JIN Xiao-guang, LI Xiao-hong, AI Ji-ren, et al. Numerical modeling of in-situ stress and surrounding rock displacement of deep-long tunnel[J]. Hydrogeology and Engineering Geology,2004(1): 40−43.
(编辑 陈灿华)
Intelligent back-analysis of tunnel surrounding rock displacement based on genetic algorithm and neural network
HUANG Kan1,2, LIU Bao-chen1, PENG Jian-guo2, FENG De-shan3, DING Guo-hua2, WANG Yue-fei2
(1. School of Civil Engineering and Architecture, Central South University, Changsha 410075, China;2. Hunan Provincial Communication Planning Survey and Design Institute, Changsha 410008, China;3. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
The learning samples and test samples were built based on orthogonal experimental design and FLAC3D numerical simulation, using the project site for the surrounding rock displacement information. The potential mapping between parameters and surrounding rock displacement was established using neural network. The results show that the optimal solution of inversion parameters can be derived to achieve the displacement back analysis combined with the genetic algorithm and prediction function of the nerve network. Then inversion results can be the feedback for the design of tunnel support structure to achieve the tunnel construction and design of information technology.
displacement back-analysis; genetic algorithm; neural network; orthogonal test
U459.2
A
1672−7207(2011)01−0213−07
2010−08−10;
2010−10−15
西部交通建设科技项目(20033179802)
黄戡(1979−),男,湖南永州人,博士研究生,工程师,从事隧道和岩土工程勘察设计与科研工作;电话:13875801586;E-mail:hk_616@sina.com

