曲线束在高考解题中的运用

●顾 慧 (青山高级中学 江苏无锡 214063) ●侯 斌 (太湖高级中学 江苏无锡 214125)

曲线束在高考解题中的运用

●顾 慧 (青山高级中学 江苏无锡 214063) ●侯 斌 (太湖高级中学 江苏无锡 214125)

1 预备知识

曲线束包括:直线束、圆束和二次曲线束．

1．1 直线束

若直线l1:a1x+b1y+c1=0与直线l2:a2x+b2y+c2=0相交于点P，则

λ(a1x+b1y+c1)+μ(a2x+b2y+c2)=0

(其中λ，μ∈R，且不全为0)表示过点P的所有直线，被称为过点P的直线束．

1．2 圆束

圆C1:x2+y2－2c1x－2d1y+f1=0与圆C2:x2+y2－2c2x－2d2y+f2=0，则

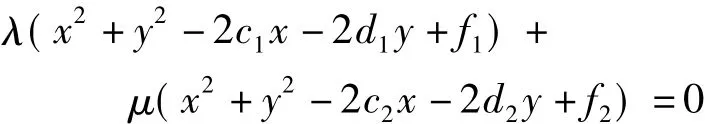
表示一族圆，被称为圆C1与圆C2的共轴圆(当λ与μ互为相反数时，被称为根轴)．

1．3 二次曲线束

2个二次曲线通常有4个交点(这些交点可能有重合的，也可能有虚的)．如果这2个二次曲线的方程分别为S1=0与S2=0(S1，S2是关于x，y的二次式)，那么通过它们交点的二次曲线束可以写成 λS1+μS2=0(其中 λ，μ∈R，且不全为0)．

2 问题提出

(3)设t=9，求证:直线MN必过x轴上的一定点(其坐标与m无关)．

本题是2010年江苏省数学高考试题第18题，这里仅考虑第(3)小题．给出的参考答案如下:

所以直线MN过点D．故直线MN必过x轴上的点(1，0)．

分类讨论和一大堆繁琐的演算背后是否忽略了某种解析几何的技巧呢?

3 用曲线束探求高考题

(1)求椭圆的方程;

(2)求证:直线PQ过定点，并求出定点的坐标．

本题是南京师范大学附属中学的一道高考模拟题，第(2)小题和2010年江苏省数学高考试题第18题第(3)小题非常相似，区别仅在于高考题将切线改为割线．

从而直线PQ过定点(1，0)．

此题解法运用了直线束的知识，绕开切点坐标的求解．2010年江苏高考题中割线和椭圆的交点是否也能绕开不求?在回答这个问题之前，先看2008年江苏省数学高考试题第9题:

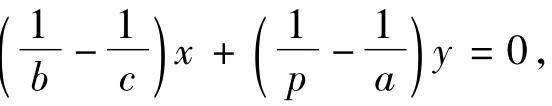
图2

图3

这2道题目都是借助直线束巧妙绕开求交点坐标的解法．以椭圆为背景的二次曲线问题可以借助于二次曲线束，省去求交点坐标繁琐的演算过程．可得过A，B，M，N这4个交点的二次曲线束．考虑其中退化为2条相交直线AB和直线MN的一条二次曲线．因为直线AB的方程不含x项，所以消去x2项，将式(1)－式(2)·化简得

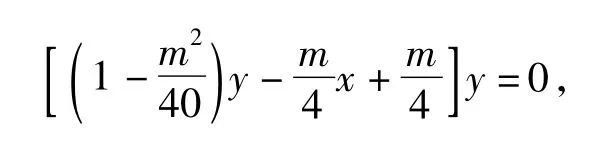
于是直线AB的方程为:y=0，直线MN的方程为:

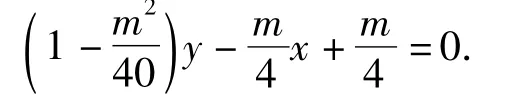
令y=0，得x=1，即直线MN恒过定点(1，0)．

4 教材中的圆束问题

《数学2》(苏教版)第2章“2．2．3圆与圆的位置关系”中的例题2:

求过点A(0，6)且与圆C:x2+y2+10x+10y=0切于原点的圆的方程．

教材中提供了2种解题思路，我们不妨再用圆束来解决这个问题．可以把切点看作是共轴圆中的一员，它是半径为0的“点圆”．

解原点可以看作是一个圆x2+y2=0，所求圆在共轴圆x2+y2+10x+10y+λ(x2+y2)=0．由于这个圆过点A(0，6)，代入方程可求出λ=－，因此可求出所求圆的方程:x2－6x+y2－6y=0．

5 结语

解题策略的选择和计算量的大小直接影响学生解析几何题的解答．针对近2年的部分解析几何高考题，笔者提出这样一个解题思路:利用曲线束，从解题技巧出发，避开繁杂的计算，可以得到比较优美的答案．

［1］ 单墫．解析几何的技巧［M］．北京:中国科学技术大学出版社，2009:38;95;137．