数学高考应用题探究

●沈顺良 (海盐县教研室 浙江海盐 314300)

数学高考应用题探究

●沈顺良 (海盐县教研室 浙江海盐 314300)

数学应用性问题是传统高考的题型之一，在新课程高考试题中有更多的体现，其涉及内容广泛，多与函数、概率统计、三角、不等式(含线性规划)、数列、解析几何等内容有机结合．新课程标准对应用意识的要求较高，给考生的阅读理解能力提出了较高的要求．在解题过程中，要求考生在陌生的现实生活情景中准确地数学化，找出数学的本质特征，建立恰当的数学模型，然后运用数学知识和工具去解决，最后结合应用问题的要求得出实际问题的解．

1 命题走势

从浙江省近2年新课程高考应用试题来看，一般理科会命制1个大题和1到2个小题，文科一般更多体现在小题中，应用题在试卷中的位置居中，显示了应用问题在高考中的基本要求．新课程教材在章序言、课题引入、例习题都突出了实际背景，还新增了“实习作业”和“研究性课题”，因此高考试题中新颖多样的应用背景成为必然．在解答应用题时，要求准确理解题意，将题中的自然语言向数学语言特别是符号语言和几何语言的转换．新课标的新增内容如概率统计、导数等本身源于现实生活问题，因此相应的应用试题在高考中频繁地出现．近年来还出现了数列、立体几何、解析几何和学科渗透的模型问题，其中大题侧重概率、导数等．

2 典例剖析

2．1 三角应用问题

例1如图1，A，B是海面上位于东西方向相距5( 3 +)海里的2个观测点，现位于点A北偏东45°，点B北偏西60°的点D有一艘轮船发出求救信号，位于点B南偏西60°且与点B相距20海里的点C的救援船立即前往营救，其航行速度为30海里/小时，该救援船达到点D需要多长时间?

(2010年陕西省数学高考理科试题)

分析本题主要考查学生运用解三角形的知识方法解决实际问题的能力．

解由题意知

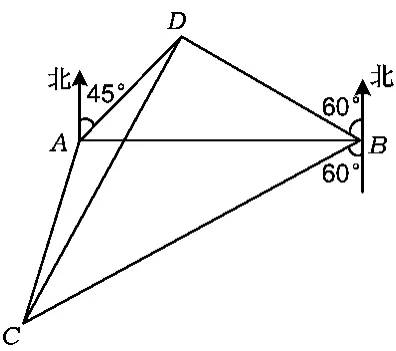
图1

故所求时间为1小时．

点评本题是一道典型的三角测量应用题，要求将题中自然语言表述的条件转换到图形语言中，然后再利用解三角形的正弦定理和余弦定理来解决，其中实际问题的条件转化是重点．

2．2 线性规划应用问题

例2铁矿石A和B的含铁率a，冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如表1所示．

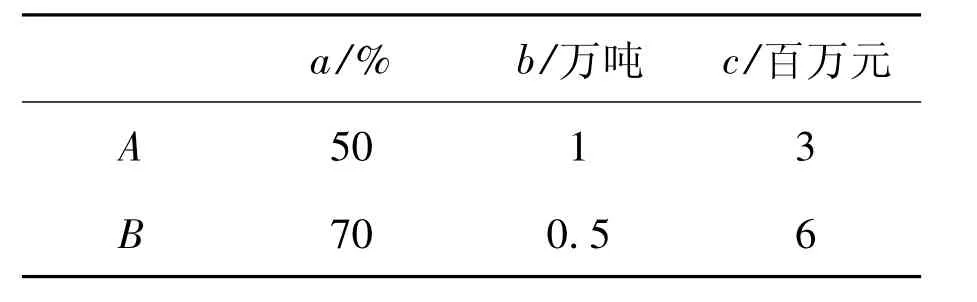
表1 铁矿石含铁率、CO2的排放量及价格表

某冶炼厂至少要生产1．9万吨铁，若要求CO2的排放量不超过2万吨，则购买铁矿石的最少费用为 ＿＿百万元．

(2010年陕西省数学高考理科试题)

解设铁矿石A购买了x万吨，铁矿石B购买了y万吨，购买铁矿石的费用为z百万元．由题设知，本题可转化为求当实数x，y满足约束条件

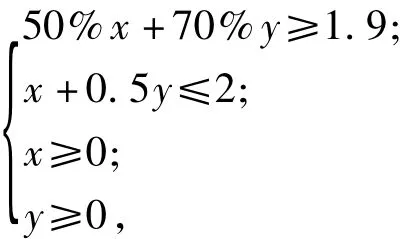
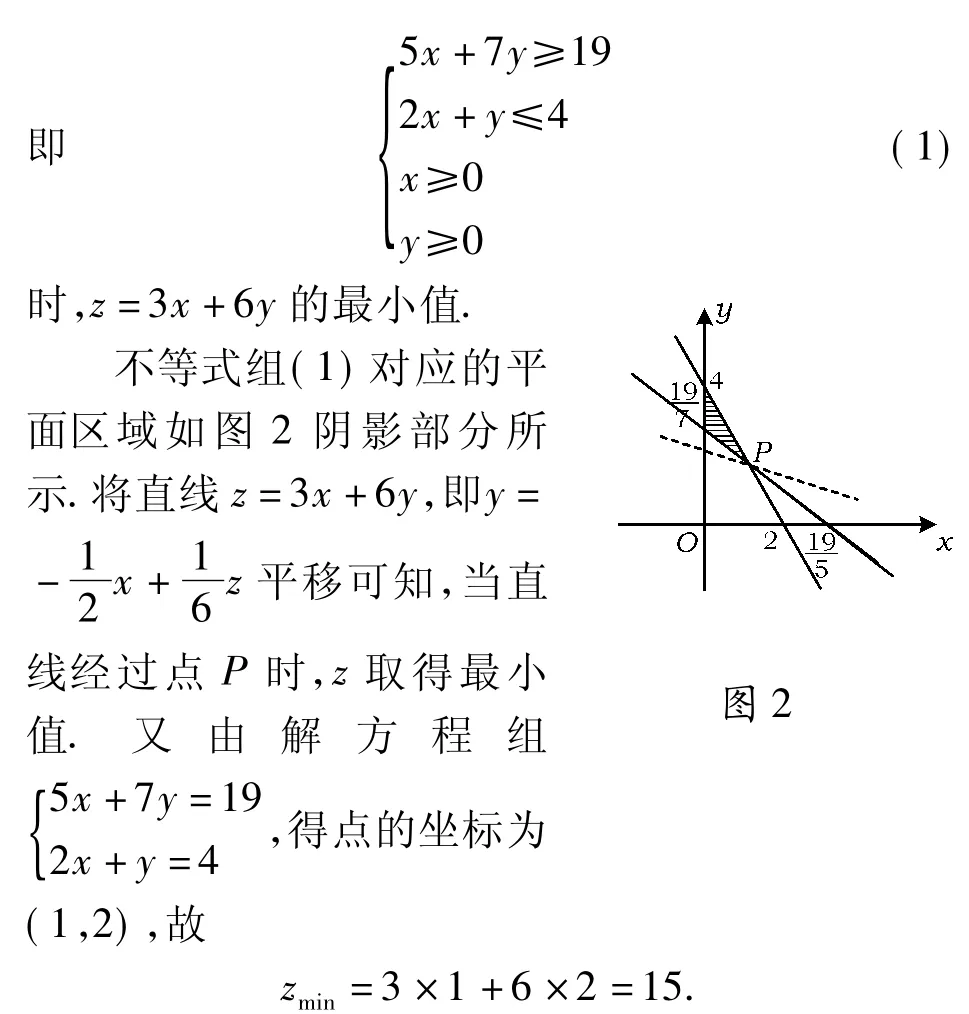
点评本题要求结合图表将给出的实际约束条件转化为数学问题并符号化，其中要特别注意实际问题中量的隐含条件，然后将数学符号语言(不等式组)转换成几何语言(线性区域)，再利用线性规划来解决．

2．3 概率统计模型

例3如图3，由M到N的电路中有4个元件，分别标为 T1，T2，T3，T4，电流能通过T1，T2，T3的概率都是 p，电流

能通过T4的概率是0．9．电流能否通过各元件相互独立．已知T1，T2，T3中至少有1个能通过电流的概率为0．999．

(1)求p;

(2)求电流能在M与N之间通过的概率．

(2010年全国数学高考理科试题)

分析本试题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及数学期望，考查分类讨论的思想方法及考生分析问题、解决问题的能力．本题也是一个与其他学科交汇的应用问题．

解记Ai表示事件:电流能通过Ti(i=1，2，3，4);A 表示事件:T1，T2，T3中至少有 1 个能通过电流;B表示事件:电流能在M与N之间通过．

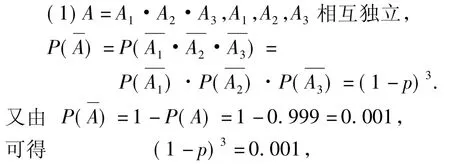
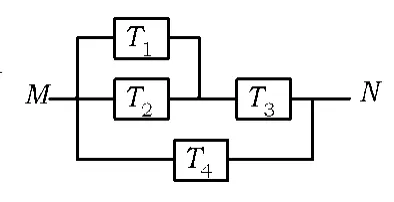
图3

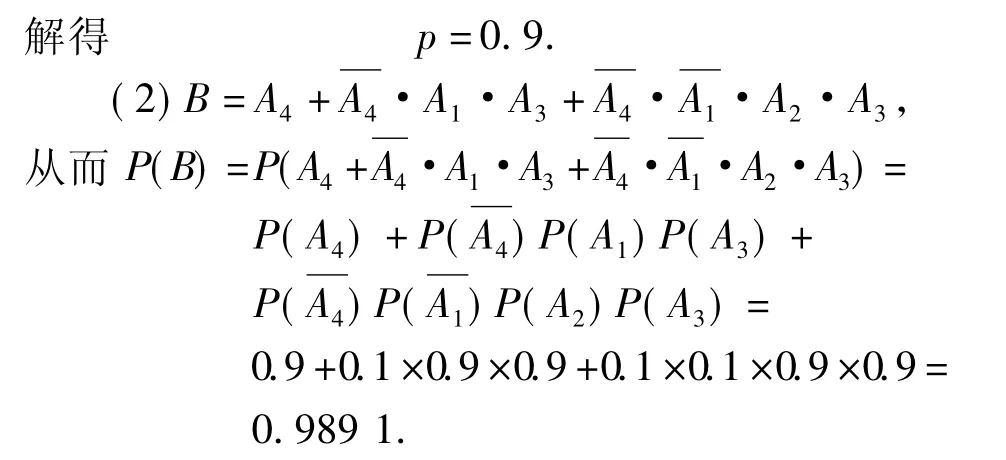
点评概率基本上是理科的必考题，问题的背景有更加丰富的趋势，对考生分析问题的能力要求也有所加强，这应引起高度重视．

2．4 计数应用问题

例4在某种信息传输过程中，用4个数字的一个排列(数字允许重复)表示一个信息，不同排列表示不同信息．若所用数字只有0和1，则与信息0110至多有2个对应位置上的数字相同的信息个数为 ( )

A．10 B．11 C．12 D．15

(2010年湖南省数学高考理科试题)

解与信息0110至多有2个对应位置上的数字相同的信息包括3类:一是与信息0110有2个对应位置上数字相同有=6个;二是与信息0110有一个对应位置上数字相同有=4个;三是与信息0110没有对应位置上数字相同有=1个，共有11个．故选B．

点评计数应用问题往往附加了多个条件，最常见的方法是对满足某个附加条件要求的情况分成若干类，分别求解后相加．在此过程中也同时考查了分类讨论思想的运用．

2．5 函数应用问题

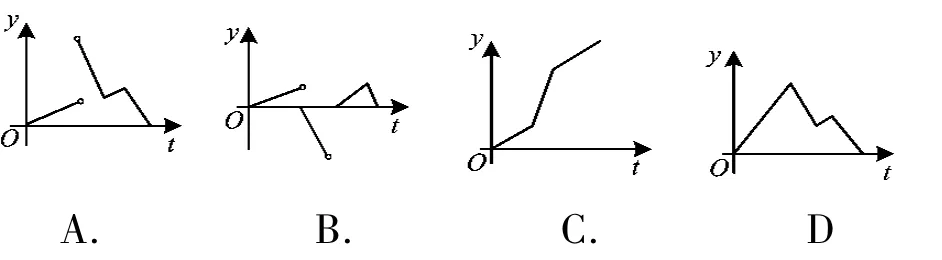
例5如图4，一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面，记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0)，则导函数y=S'(t)的图像大致为

图4

(2010年江西省数学高考理科试题)

分析本题考查函数图像、导数图像、导数的实际意义等知识．最初0时刻和最后终点时刻没有变化，导数取0，排除选项C;总面积一直保持增加，没有负的改变量，排除选项B;考察选项A，D的差异在于两肩位置的改变是否平滑，考虑到导数的意义，判断此时面积改变为突变，因此产生中断．故选A．

点评导数有其丰富的现实背景，本题正是通过结合生活实际中的变化过程，考查对导数几何意义和现实意义的理解．

2．6 解析几何应用问题

例6为了考察冰川的融化状况，一支科考队在某冰川上相距8 km的点A，B处各建一个考察基地．视冰川面为平面形，以过点A，B的直线为x轴，线段AB的垂直平分线为y轴建立平面直角坐标系．在直线的右侧，考察范围为到点B的距离不超过km的区域;在直线x=2的左侧，考察范围为到点A，B的距离之和不超过4km的区域．

(1)求考察区域边界曲线的方程;

(2)如图5，设线段P1P2，P2P3是冰川的部分边界线(不考虑其他边界)，当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0．2 km，以后每年移动的距离为前一年的2倍，求冰川边界线移动到考察区域所需的最短时间．

(2010年湖南省数学高考理科试题)

解(1)设边界曲线上点P的坐标为(x，y)．当x≥2时，由题意知

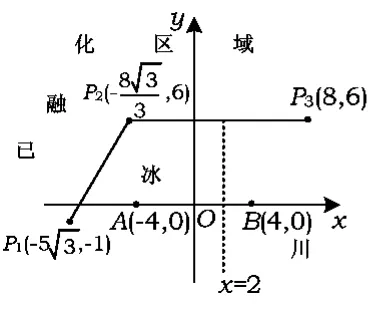
图5

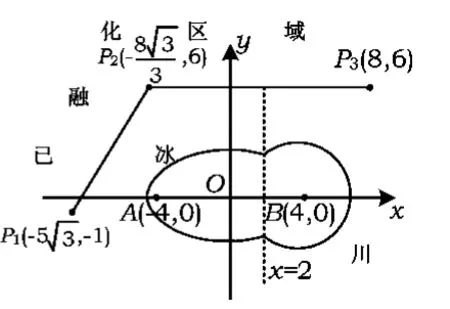
图6

(2)设过点 P1，P2的直线为 l1，过点 P2，P3的直线为l2，则直线l1，l2的方程分别为y=+14，y=6．设直线l平行于直线l1，其方程为y=+m，代入椭圆方程消去y得由判别式等于0，解得

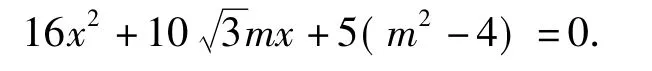
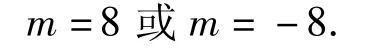
从图6中可以看出，当m=8时直线l与C2的公共点到直线l1的距离最近，此时直线l的方程为y=+8，l与l1的距离为3．因为直线l2到C1和C2的最短距离为6－＞3，所以考察区域边界到冰川边界的最短距离为3．

设冰川边界线移动到考察区域所需时间为n年，则由题设及等比数列求和公式得:

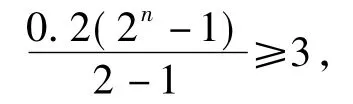
解得n≥4，即冰川边界线移动到考察区域所需的最短时间为4年．

点评本题以实际探究问题为背景，考查数学建模能力，知识涉及圆方程、椭圆的定义与方程、直线与圆锥曲线的位置关系、等比数列求和等．题中已经给出直角坐标系，要求根据题中实际条件求出相应的直线、圆、圆锥曲线方程，并用它们来解决问题．

除了上述典型实例，另外还有数列模型、立体几何模型等数学模型的应用问题，也有物理等其他学科背景的应用问题．

精题集粹

1．某台小型晚会由6个节目组成，演出顺序有如下要求:节目甲必须排在第4位、节目乙不能排在第1位，节目丙必须排在最后一位，该台晚会节目演出顺序的编排方案共有 ( )

A．36种 B．42种 C．48种 D．54种

2．为了迎接2010年广州亚运会，某大楼安装了5个彩灯，它们闪亮的顺序不固定，每个彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色，且这5个彩灯所闪亮的颜色各不相同．记这5个彩灯有序地闪亮一次为一个闪烁，在每个闪烁中，每秒有且仅有一个彩灯闪亮，而相邻2个闪烁的时间间隔均为5秒．如果要实现所有不同的闪烁，那么需要的时间至少是 ( )

A．1 205秒 B．1 200秒 C．1 195秒 D．1 190秒

3．一质点受到平面上的3个力 F1，F2，F3(单位:牛顿)的作用而处于平衡状态．已知F1，F2成角60°，且 F1，F2的大小分别为 2 和 4，则 F3的大小为 ( )

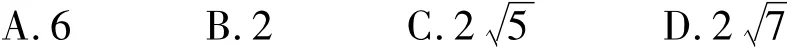
4．某加工厂用某原料由甲车间加工出产品A，由乙车间加工出产品B．甲车间加工一箱原料需耗费工时10小时可加工出7千克产品A，每千克产品A获利40元．乙车间加工一箱原料需耗费工时6小时可加工出4千克产品B，每千克产品B获利50元．甲、乙2车间每天共能完成至多70箱原料的加工，每天甲、乙2车间耗费工时总和不得超过480小时，甲、乙2车间每天总获利最大的生产计划为 ( )

A．甲车间加工原料10箱，乙车间加工原料60箱B．甲车间加工原料15箱，乙车间加工原料55箱C．甲车间加工原料18箱，乙车间加工原料50箱D．甲车间加工原料40箱，乙车间加工原料30箱5．某班共有30人，其中有15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这2项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为＿＿．6．某工厂生产甲、乙2种产品，产品甲的一等品率为80%，二等品率为20%;产品乙的一等品率为90%，二等品率为10%．生产1件产品甲，若是一等品则获得利润4万元，若是二等品则亏损1万元;生产1件产品乙，若是一等品则获得利润6万元，若是二等品则亏损2万元．设生产各种产品相互独立．

(1)记X(单位:万元)为生产1件产品甲和1件产品乙可获得的总利润，求X的分布列;

(2)求生产4件产品甲所获得的利润不少于10万元的概率．

参考答案

1．B 2．C 3．D 4．B 5．12

6．(1)X的分布列如表2所示．

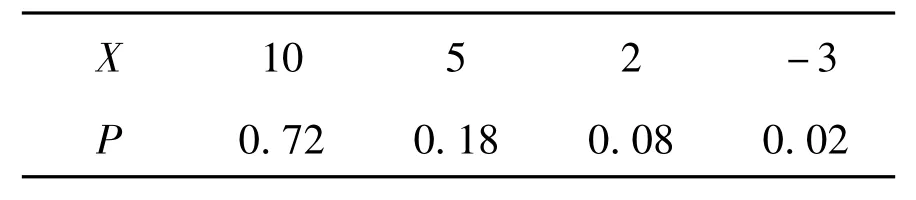
表2 X的分布列

(2)生产4件甲产品所获得的利润不少于10万元的概率为0．819 2．