隐性路径 显性分析

●周礼寅 (东台市实验中学教育集团 江苏东台 224200)

运动型问题是近年来中考的一个热点.这类试题能全面考查学生的数学活动过程，考查学生通过数学思考解决问题的综合应用能力，因而倍受各地中考命题者的青睐.探索在运动过程中动点的运动路径是运动型问题新呈现的考查方向.这类问题由于动点运动路径不明晰，因此对学生分析问题的能力要求更高.为此，本文尝试对这类隐性路径问题进行显性分析，供参考.

1 动点路径问题的几种类型

1.1 单动点路径

例1 如图1，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止，连结EM并延长交射线CD于点F，过点M作EF的垂线交射线BC于点G，连结EG，FG.

(1)设AE=x，△EGF的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围;

(2)P是MG的中点，请直接写出点P的运动路线的长.(2010年江苏省南京市数学中考试题)

分析(1)略;

(2)要求点P的运动路线的长，必须先探索点P的运动轨迹.由动点E运动的临界点为A，B，可知当动点E运动至点A时，点P运动至点P1(如图2);当动点E运动至点B时，点P运动至点P2(如图3)，因此点P在P1与P2之间运动.

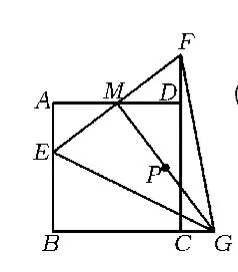
图1

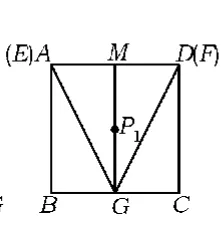
图2

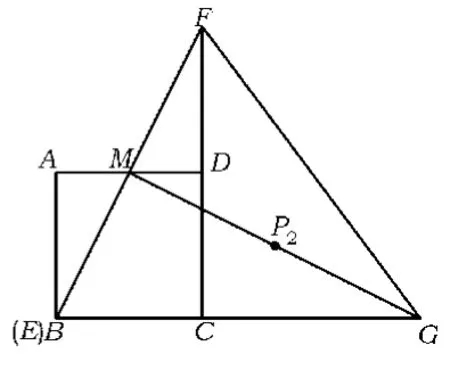
图3

在由点A向点B运动的过程中，再选取一个动点E，作出相应的点 P(如图4)，从点 P1，P，P2可大致猜测出点P的运动轨迹应为线段P1P2.

为什么点P的运动轨迹为线段P1P2呢?如图5，设 MG交 P1P2于点 P'.由 P1P2为△MG1G2的中位线，得 P1P2∥G1G2，即 P1P'∥G1G2，因此即点P'与点P重合.这表明MG的中点P始终落在线段P1P2上，因此点P的运动路径为P1P2，通过计算可求得P1P2的长为2.

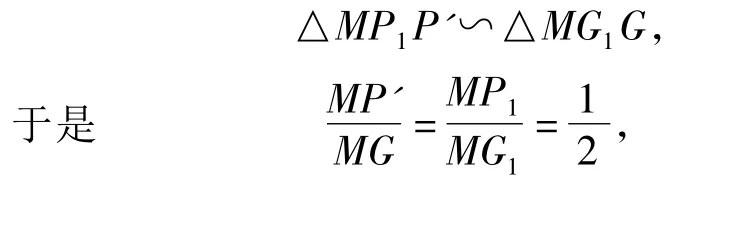
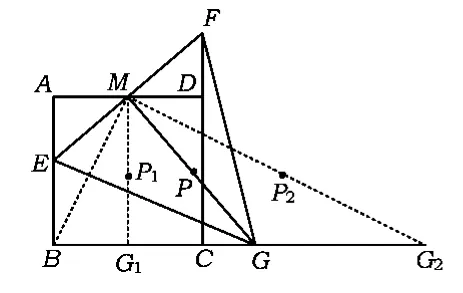
图4

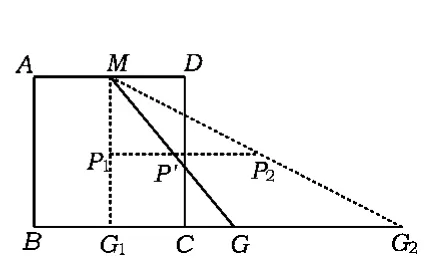
图5

评析 本题由于动点E的运动，使得△EFG及点P均受点E的牵制而运动.在探索动点P的运动路径时，其分析思路为：特殊位置找界点，中间位置寻轨迹，一般位置探成因.这种分析方法适用于一般的运动路径探索问题.

该试题是全卷的压轴题，给学习能力较强的学生创造了展示自我的空间，通过动态探究问题来考查学生的逻辑推理能力、探究发现能力、灵活利用数学知识解决问题的能力，是考查学生综合能力和数学素养的一道关键题目，同时兼顾高一级学校选拔新生的需要.

1.2 双动点路径

例2 如图6所示，已知AB=10，点C，D在线段AB上且AC=DB=2.P是线段CD上的动点，分别以AP，PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为G.当点P从点C运动到点D时，则点G 移动路径的长是_______.

(2010年广西省桂林市数学中考试题)

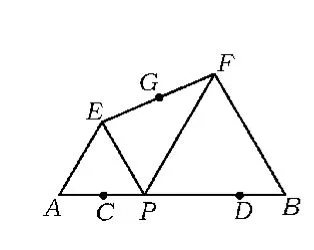
图6

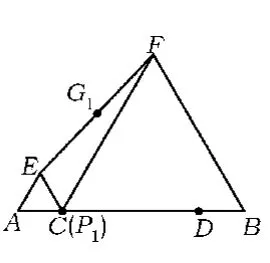
图7

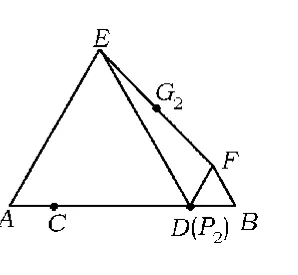
图8

分析由于点P从点C运动到点D，其运动的临界点为C，D.当动点P运动至点C时，点G运动至点G1(如图7);当动点P运动至点D时，点G运动至点G2(如图8).因此点G在G1与G2之间运动.

为了探明动点G的运动轨迹，在由点C至点D运动的过程中，再选取点P的某一位置作出相应的点G(如图9)，由点G，G1，G2可大致判断点G的运动轨迹应为线段G1G2.

为说明点G总在线段G1G2上运动，如图10，延长AE，BF交于点H，则 PE∥FH且 PF∥EH，得四边形PEHF为平行四边形.由点G为EF的中点，得点G为▱PEHF对角线的交点，因此点G一定为HP的中点.随着点P在CD上运动，由例1第(2)小题的分析可知，中点G在线段G1G2上运动.而线段G1G2为△HCD的中位线，其长度为3.

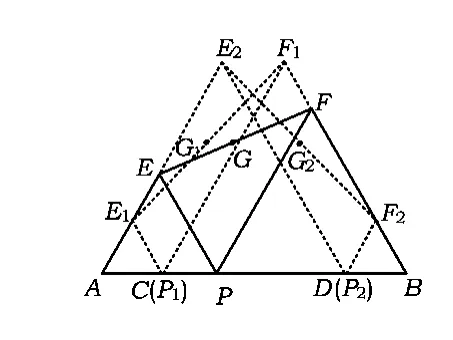
图9

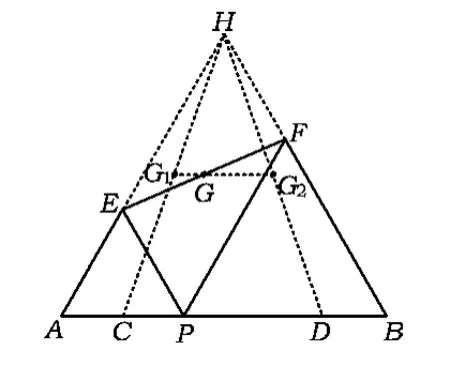
图10

评析 本题打破过去单纯从动点、动直线的角度切入的常规方法，而是借助双动点使两点运动牵制形成另一动点的构思新颖的运动状态，尝试从不同角度考查学生采集“数”与“形”的信息，寻求解决问题方法的能力.试题还考查了等边三角形、平行四边形和相似形的性质;考查了运动变化思想和数形结合思想，以及特殊与一般、运动与变化等数学观念，确保了试题在《课程标准》的要求范围内具有较高的区分性和较好的效度.

1.3 动图形路径

例3 已知：如图11，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=6，BC=8，AD=14.E 为AB上一点，BE=2，点F在边BC上运动，以FE为一边作菱形FEHG，使点H落在边AD上，点G落在梯形ABCD内或其边上.若BF=x，△FCG的面积为y.

(1)当x = _______时，四边形FEHG为正方形;

(2)求x与y的函数关系式(不要求写出自变量的取值范围);

(3)在备用图中分别画出△FCG的面积取得最大值和最小值时相应的图形(不要求尺规作图，不要求写画法)，并求△FCG面积的最大值和最小值(计算过程可简要书写);

(4)△FCG的面积由最大值变到最小值时，点G 运动的路线长为_______.

(2010年北京市西城区八年级期末测试卷)

分析(1)，(2)略.

(3)如图11，过点G作GM⊥AD于点M，并反向延长交BC于点N，连结HF，可证得

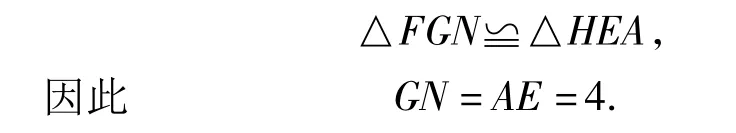
在△FCG中，边FC上的高GN不变，要使其面积最大(小)，只需底边FC的值最大(小).当点F运动到使菱形FEHG的顶点H与点A重合时(如图12)，FC取得最大值.在Rt△BEF中，求得

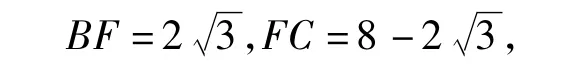
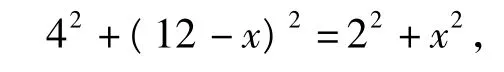
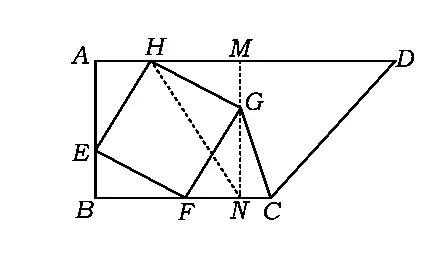
图11

(4)由第(3)小题知，点G在G1与G2间运动.如图12，无论点 F如何运动变化，它到边BC的距离始终不变，点G的运动轨迹为与直线BC平行，且到直线BC的距离为4的平行线段G1G2，通过计算可求得G1G2的长为 1 2-2.

评析 该试题通过点F的运动带来菱形与三角形的运动，把观察、操作、探究、计算融合在一起，将全等三角形、菱形、勾股定理等初中数学的主干知识融为一体.作为压轴题，本题设计新颖、不落俗套、自然流畅、梯度合理、入口宽、出口窄，需综合运用核心知识去灵活地解决问题.在探究图形变化过程中，考查了函数思想、方程思想等重要的数学思想方法以及基本轨迹的识别与应用.

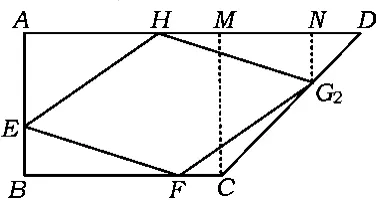
图12

1.4 坐标系路径

例4 如图14，在平面直角坐标系中，已知点A(2，4)，B(5，0)，动点P 从点B 出发沿BO 向终点O运动，动点Q从点A出发沿AB向终点B运动.两点同时出发，速度均为每秒1个单位，设从出发起运动了x秒.

(1)点Q的坐标为( _____，______)(用含x的代数式表示);

(2)当x为何值时，△APQ是一个以AP为腰的等腰三角形?

(3)记PQ的中点为G，请你探求点G随点P，Q运动所形成的图形，并说明理由.

(2006年江苏省苏州市数学中考试题)

分析(1)，(2)略.

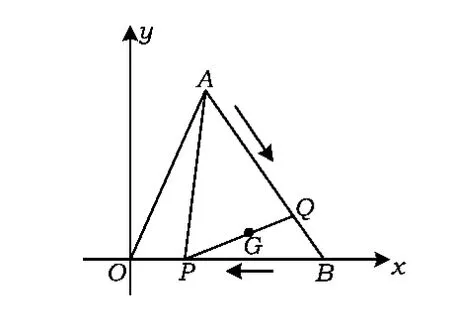
图14

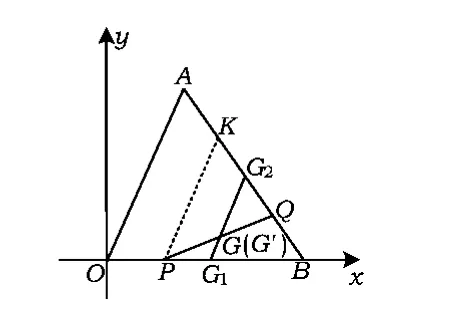
图15

(3)由于P，Q的运动速度相同，且AB=OB，因此点P从点B运动至点O的同时，点Q从点A运动至点B.当动点P与点B重合时，点G为AB的中点G2;当动点P与点O重合时，点G为OB的中点G1.再在OB上选一点P，作出相应的点Q及PQ的中点G.由点G1，G，G2观察可发现点G随点P，Q运动所形成的图形是线段G1G2(如图15).下面进一步说明点G的运动轨迹为线段G1G2.

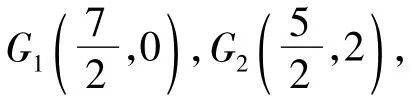
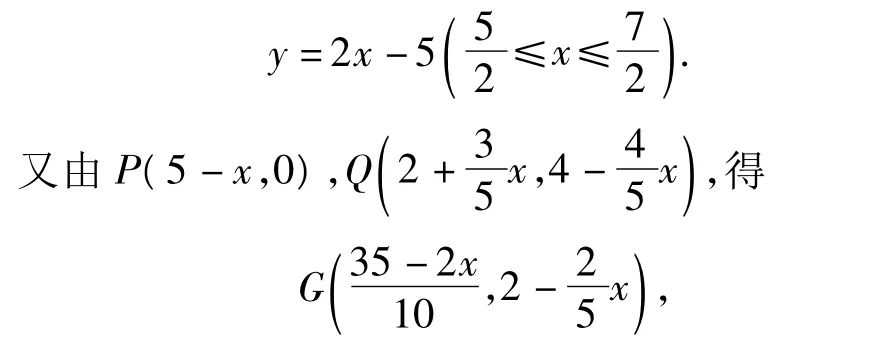
满足y=2x-5，因此点G在线段G1G2上.

思路2 如图15，设G1G2与PQ交于点G'，过点P作 PK∥AO交 AB于点 K.由 PK∥AO，得△AOB∽△KPB.又由△AOB∽△G2G1B，AB=OB，

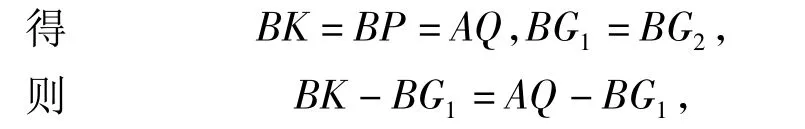
即 KG2=QG2.由 G2G'∥PK，得△QG2G'∽△QKP，因此PG'=QG'，即G'是PQ的中点，故点G'与点G重合，点G在线段G1G2上.

评析 思路1是在直角坐标系中，根据点G的坐标满足线段G1G2的直线方程，说明点G在线段G1G2上;思路2通过证明PQ与G1G2的交点为PQ的中点，得到点G的运动轨迹是线段G1G2.试题以坐标系、三角形、函数解析式等数学知识为立足点，加大了对后续学习的分类讨论、数形结合、函数方程等数学思想方法的考查，体现了初、高中教学内容的衔接.通过问题的解决还有效地考查了学生在数学活动过程中所表现出的思维方式、思维水平，对教学起到了导向作用.

2 动点路径的特征及解题思路

以上几例的共同特点是：在几何图形中或函数图像上，有1或2个动点沿线段、折线、射线或圆弧等曲线运动，研究点在运动中牵制形成另一相关联的动点的运动路径形状或路径的长.

对这类问题要善于借助动态思维的观点来分析，不为“动”所迷惑.从特殊情形入手，变中求不变，动中求静，抓住静的瞬间，以静制动，把动态问题转化为静态问题来解决，从而找到问题的突破口.动与静是相对的，抓住运动中的不变量(譬如图形全等、距离不变等)，对比运动前后2种状态的区别，用心体会，寻找规律.解答时往往需要综合运用转化思想、数形结合思想、方程函数思想及分类讨论等各种数学思想方法.

图16

3 实战演练

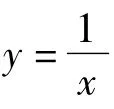
A.直线 B.抛物线 C.圆 D.双曲线

(2007年浙江省慈溪市慈溪中学初中保送生招生考试数学试题)

提示延长BF，交AC的延长线于点G，连结OF，则

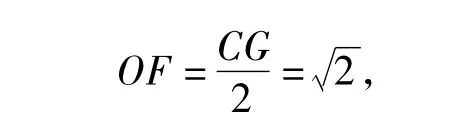
［1］ 张晓林.中考典型问题备考系列——动态几何型［J］.中学数学教学参考，2009(1-2)：100-104.

［2］ 李梦虎.例析动态问题认知模式的提炼［J］.中国数学教育，2009(12)：29-30.