探究例题内涵 彰显数学魅力——对一道课本习题的变式教学

● (温岭市实验学校 浙江温岭 317500)

探究例题内涵彰显数学魅力
——对一道课本习题的变式教学

●童鹏(温岭市实验学校 浙江温岭 317500)

叶圣陶先生曾说：“教材只能作为教课的依据，要教得好，使学生受到实益，还要靠教师的善于运用”．教材是教学的重要资源,课本中的每一个例题和习题都是经过“千锤百炼”的，有很高的教育价值．教师在现实教学中，如何就有限的教学资源，充分加以利用，并时常保持数学独特的魅力，变题是一种好方法．下面笔者以一道具体的课本习题为例谈一谈教学资源的整合和对其教育价值的挖掘,供参考．

原题如图1，在正方形ABCD中，点E，F分别在边BC，CD上，AE，BF交于点O，∠AOF=90°，求证：BF=AE.

本题源于人教版《数学》八年级下册.学生基本上能利用互余找到2组相等的角，从而证明△ABE≌△BCF，再利用全等可得BF=AE．

图1 图2

1 探究例题,用变题开拓思维

教材提供的仅仅是一种方向，一条线索，教师在面对教材时，完全可以根据实际需要对其进行增添、删减、调整、变换、延伸等“艺术”加工，赋予它新的生命，从而达到真正意义上的利用教材．

1．1 探究删减条件的变题

在完成原题的解答后，出示下面的演变1.

演变1如图2，在正方形ABCD中，点E，F，G，H分别在边AB，CD，AD，BC上，EF，GH交于点O，∠FOH=90°，求证：EF=GH.

师：当这2条线段的端点分别在正方形的边上时，线段还会相等吗？

生：会．

师：怎么得到相等呢？

生：构造一对全等的三角形．过点A作AM∥GH交BC于点M，过点B作BN∥EF交CD于点N，则四边形AMHG和四边形BNFE均为平行四边形，那么图形就和图1一样了，证明方法也一样．

师：不错，该同学把图2转化到熟悉的图1，问题自然解决了．

生：也可以过点G作GM⊥BC于点M，过点F作FN⊥AB于点N(如图3)，则△FNE≌△GMH，可得EF=GH．

师：这2个三角形全等的条件充分吗？

生：充分.因为GM∥AB，FN∥AD，所以FN⊥GM，∠FQH+∠QFO=90°，∠QGP+∠GQP=90°.又因为∠FQH=∠GQP，所以∠QFO=∠QGP，从而△FNE≌△GMH．

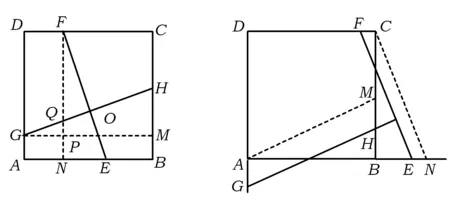
图3 图4

师：点在边上移动着，能否移到边所在的直线外呢？当这些点分别在它们所在的直线上运动时，是否只要保持GH与EF垂直，GH与EF就相等呢？

生：都可以证明.如图4，过点A作AM∥GH交BC于点M，过点C作CN∥EF交AB于点N，则四边形AMHG和四边形CNFE均为平行四边形，利用图1的方法可证明△ABM≌△BCN，得GH=EF．

师：思路非常好，把后面的2个图形都转化成图1来解决.虽然点在变，但是基本图形不变，因此结论也不变．

适当删减条件，可把题目从特殊转化为一般.本例从点移到边，再移到直线上，完成了从静到动的演绎，使学生经历了一个变化、灵动的过程.这种融知识性、趣味性、开放性、挑战性于一体的习题，学生不会觉得是一种负担，而是一种乐趣，真正体现了在数学活动中理解和掌握数学知识的理念．

1．2 探究增加条件的变题

演变2(在图2的基础上改题)如图5，在正方形ABCD中，点E，F，G，H分别在边AB，CD，AD，BC上，EF，GH交于点O，且∠FOH=90°.若点O刚好是正方形的中心，求证：DF=AG=BE=CH.

学生思考一段时间后.

生：连结GF，FH，HE，GE，可证得△DFG，△CFH，△BHE，△AEG全等.

师：怎样证明？条件分别是什么？

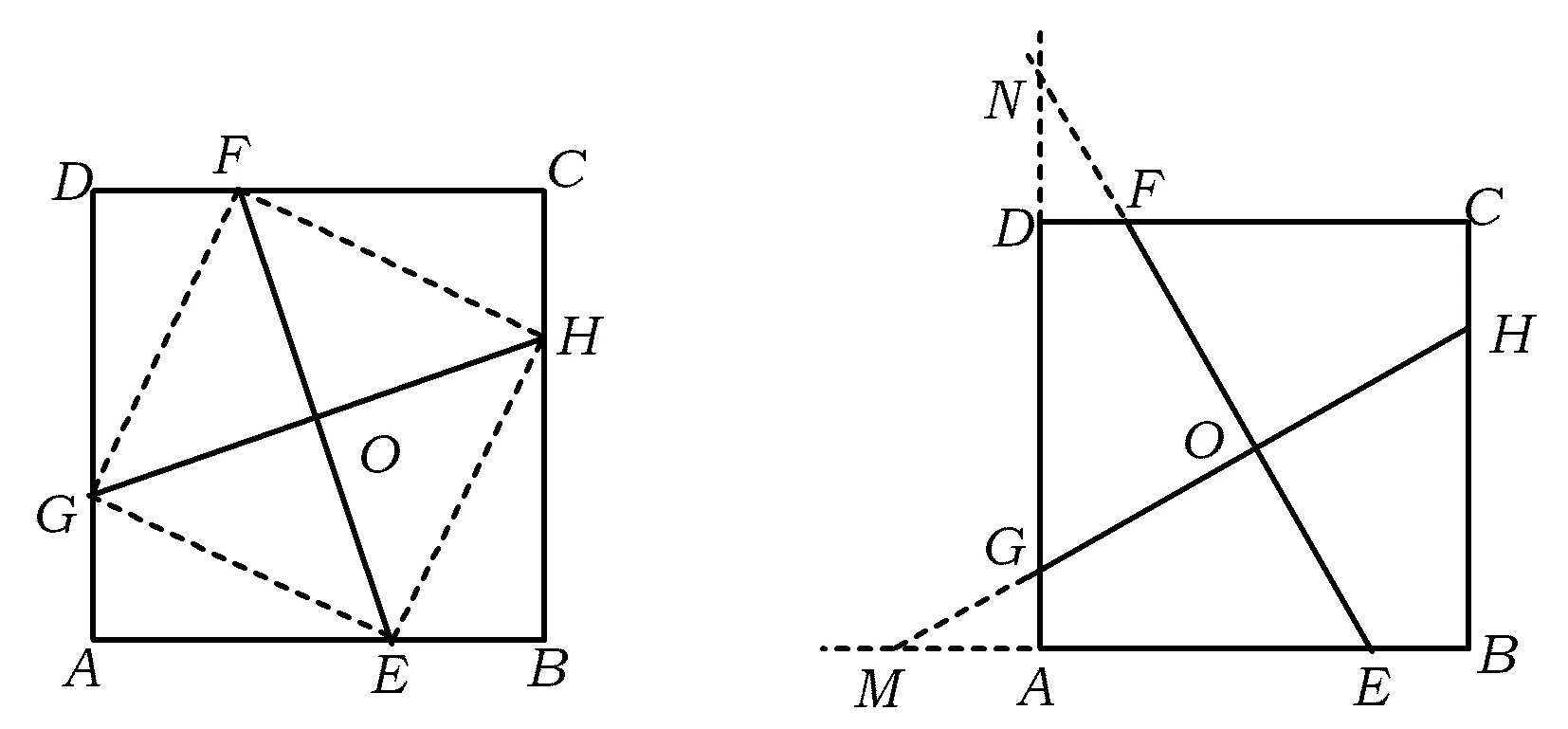
图5 图6

生：因为EF⊥GH，且点O是正方形的中心，所以EF与GH相互垂直平分，再利用图2的证明，可知EF=GH，于是四边形EHFG是正方形，得

GF=FH=EH=GE．

再利用角度的互余关系得

∠DFG=∠CHF=∠BEH=∠AGE,

利用直角的条件，即可证得三角形全等．

师：正方形ABCD被EF和GH分成的4个部分有何关系呢？

生：这4个部分是全等的．

师：(在图5的基础上增加条件的变题)如图6,如果延长EF，HG分别交AD和BA的延长线于点N，M，那么AM和DN会相等吗？

生：会．可证得△BHM≌△AEN.

师：运用哪些条件证明全等呢？

生：由图5得

AE=BH，∠AEF=∠BHG.

又由∠ABC=∠DAB=90°，可得三角形全等，于是AM=DN．

适当增添条件，可以得到更多的结论，从而考验学生对知识掌握的全面性，因此对学生掌握知识的要求较高，往往要把所学知识贯穿起来.图4的变形是一个一般的图形，在证明线段相等时，学生自然地想到了用三角形全等的方法.图5是一个图形的拓展延伸，基本结论更加清晰、明了．因此在课堂教学中，要注意把所遇到的问题与基本问题相联系，并作一定的拓展，对提高学生思维的广阔性很有帮助．

1．3 探究变换图形的变题

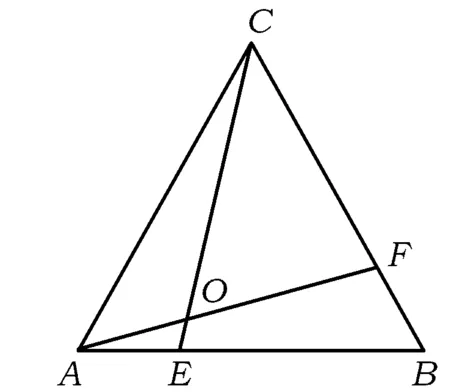
图7

演变3(1)如图7，若将原题中的条件“正方形”改为“正三角形”，“2条线段的交角为直角”改为“交角为60°”，即“AE⊥BF”改为“∠COF=60°”，其他条件不变，则原题的结论还成立吗？如果成立,请给出正面证明;如果不成立,请给出反例．

师：这一题进行了图形的改变，把正方形换成了正三角形，AE⊥BF改为∠COF=60°，这时AF与CE是否还会相等？

生：只要能够证明△ACE≌△BAF即可.

师：能找到三角形全等的条件吗？

(经过一段时间的讨论.)

生：条件足够．有一对角一组边相等，只要再得一对角相等就可以了．因为

∠CAO+∠ACO=60°,∠CAO+∠OAB=60°,

所以

∠ACO=∠OAB，

于是

△ACE≌△BAF.

师：进一步如果将原题中的条件“正方形”改为“正五边形”，那么请你模仿原题写出一个真命题，并在图8中画出相应的图形．

(学生能够很自然地得出此题的答案.)

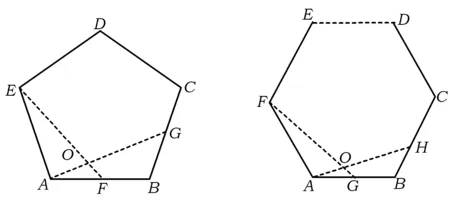
图8 图9

生：在AB上取一点F，连结EF，过点A作AG，且使得∠EOG=108°，那么EF=AG．证明方法与上一题一样，只是角度发生变化了．

师：是否还有其他的延伸呢？

(学生立刻进行探讨，并且很快得到了问题的答案.)

生：正六边形也是可以的，只要把夹角改为120°就可以了．

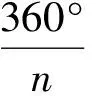
图形虽然在变，但万变不离其宗，解题的方法没变．正方形是特殊的正多边形，本题从正方形具有的一般性结论自然地类比到了其他的正多边形，再进行相似探索、思考、研究相应的结论.这种推广过程可使学生理解特殊与一般的辨证关系，从而培养学生类比、推理、分析的综合能力，让学生的思路豁然开朗．

1．4 探究图形延伸的变题

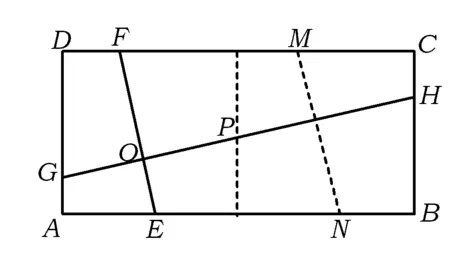
图10

演变4已知点E，F，G，H分别在矩形ABCD的边AB，BC，CD，DM上，EF，GH交于点O，∠FOH=90°，EF=4.

(1)如图10，矩形ABCD由2个全等的正方形组成，求GH的长;

(2)如图11，矩形ABCD由n个全等的正方形组成，求GH的长(用n的代数式表示).

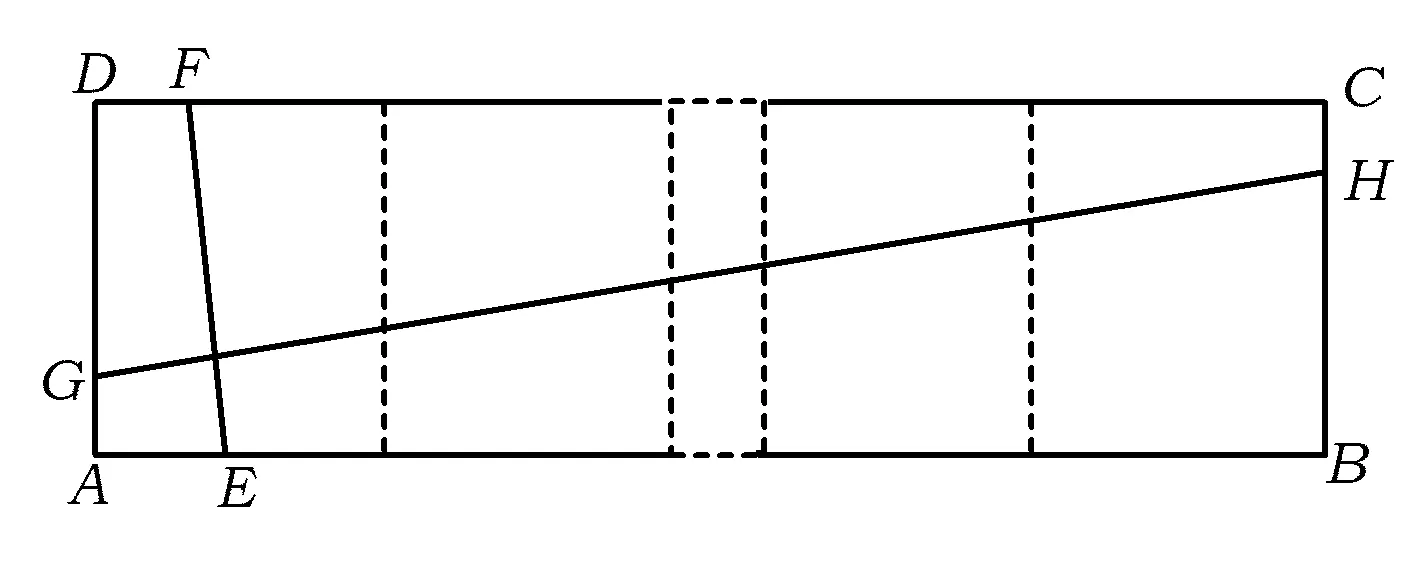
图11

师：请同学们观察，2个正方形拼接在一起，但仍然保持∠FOH=90°不变，这时EF与GH会相等吗？如果不相等，那么它们会有怎样的关系？

(学生经过一段时间思索后)

生：图4与图2非常相似，能不能把图10转化为与图2相似的图形呢？

生：可以先用其中一个正方形，设GH交正方形的一边为点P，则GP=EF．

师：在另一个正方形中的部分怎么办呢？

生：可以构造如图1的图形．在边上任意找一点M，再过点M作MN∥EF，得到EFMN，于是EF=MN，MN⊥PH，再利用图1的结论可得MN=PQ=EF=GP，从而GH=2MN．

师：非常好!若能想到把这个图形看成是2个图1的组合，则转化的思想显而易见了．

师：如果矩形ABCD由n个全等的正方形组成(如图11)，那么GH与EF又有怎样的关系呢？

生：GH=nEF.由前面的探讨可得每个正方形内的一部分等于EF，总共有n个正方形，因此GH是EF的n倍．

这便是从部分到整体的变通，是一种质的飞跃，起到了“画龙点睛”的作用！让学生全面、深刻地看到课本习题的全貌和问题的本质,通过合理整合教学资源，巧用问题串使问题轻松解决．

对教材资源的变题是对教材资源的再创新.在保留部分原题的前提下，将问题逐步引申、挖掘，深化了题目的内涵，对学生思维的广阔性、灵活性和创造性都起到了很大的作用.

2 反思例题，用变题激发潜能

以上对一道习题进行了4次深入的探究，从不同的角度进行了变题，纵横发散、沟通，层层深入，将问题合理演化、凝题成链、织题成网，使学生在倾听中产生灵性，在思考中展现智慧，在体验中生成情感，在相互尊重中绽放灿烂的生命之花．

2．1 妙用例题，让学生讨论变题

在教学过程中，教师可以充分利用学生资源，营造自然、生动的教学氛围，以激发学生的学习兴趣，为其创造真实运用数学的外部条件.在这次的例题教学中让学生讨论变题，应学生而动、应情境而变，使课堂焕发了生命的活力.

例如演变1的教学过程：先由线段EF和GH的端点在正方形的顶点上，结论EF=GH成立，然后逐步地使2条线段的端点从顶点移到边上，再进一步地移到边的延长线上，使学生的思维不断地被激发，也让他们非常迫切地想知道结论是否还成立.这就引起了学生的兴趣.学生通过对知识的需求，演绎讨论的过程，从而获得正确的结论.这无疑展示了一种活跃的思维过程，培养了学生思维的发散性.

2．2 妙用例题，让学生参与变题

通过对例题的潜心挖掘和学生的参与变题，使题目由一道题变成了一类题，大大地提高了双基的容量和灵活性，从而锻炼了学生思维的广泛性，提高了举一反三、触类旁通的能力，而这正是思维灵活性得到培养和发展的最好体现.

例如演变3的教学过程：先由图形是正方形，得结论AE=BF成立.再考虑:当正方形演变成正三角形，2条线段夹角为多少度时，结论仍然成立？到此，学生就会进一步地自己参与变题，联想到其他的正多边形是否也有类似的结论.通过一题多变，让学生积极地参与到变题中，深刻地挖掘了例题的内涵，从而达到培养学生良好思维方式和创新意识的目的.

新课标强调，学生是学习的主人，教师要鼓励学生质疑、探究，在思考的过程中感受和体验数学知识产生、发展的过程．数学问题的探究往往是无穷尽的.通过变题，既能使学生高瞻远瞩，又能有效地学习，从而提高学习效率．若教师在课前充分挖掘教材资源,在课堂中利用变题引导学生探索，则能激发他们的兴趣，甚至让学生学会变题．这样不仅能巩固知识，挖掘不同知识点间的联系，而且能开拓学生的思维和视野，有事半功倍之效．

总之，在例、习题教学中，教学资源无处不在、无时不生、取之不尽、用之不竭．教师要不断地探索、实践、反思，探究教学资源，妙用课堂资源．要贯彻新课程的教学理念，发挥例、习题应有的教学价值，实施例、习题教学的有效性，深入探究例、习题蕴涵的宝藏，彰显数学独特的魅力．

[1] 王丽君.例题教学的四重探究[J].中学数学教学参考，2010(5):37.

[2] 吴莉霞，刘斌.变式教学要把握三个“度”[J].数学通报，2006(4):26.

[3] 王峰.莫让浮云遮望眼 撩开雾纱见真颜[J].中学数学教学参考，2010(6):51.