函数复合最值问题的常用求解策略

●高 召 (三门峡市第一高级中学 河南三门峡 472000)

函数复合最值问题的常用求解策略

●高 召 (三门峡市第一高级中学 河南三门峡 472000)

在数学竞赛和高考题中，常常会遇到一些在一类最大值中求其最小值或在一类最小值中求其最大值的复合最值问题．它是函数最值问题中的一种特殊类型，解决这类问题的方法也比较特殊．本文介绍了解决此类问题的一些常用策略，供参考．

1 图像法

例1用 min{a，b，c}表示 a，b，c这 3 个数中的最小值．设 f(x)=min{2x，x+2，10 － x}(x≥0)，则f(x)的最大值为 ( )

A．4 B．5 C．6 D．7

(2009年宁夏、海南数学高考试题)

分析作出函数y=2x，y=x+2，y=10 － x的图像，如图1所示．由图像可得，f(x)的解析式为

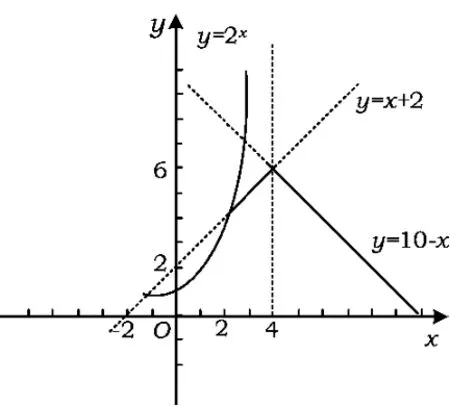
图1

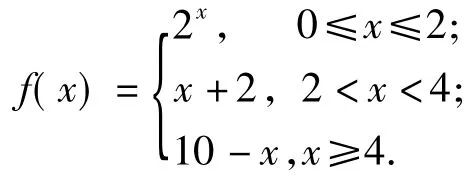
观察f(x)图像的最高点，得f(x)max=6．故选 C．

注对于涉及一元变量的多个函数的复合最值问题，采用图像法求解会更加直观、简洁．

2 均值法

利用平均值是处理函数复合最值问题的最常用方法，往往选取算术平均值和几何平均值进行求解．若 M=max{x1，x2，…，xn}，m=min{x1，x2，…，xn}，设 x1，x2，…，xn的算术平均值为 A，则 m≤A≤M．设正数 x1，x2，…，xn的几何平均值为 G，则 m≤G≤M．

注对于涉及多变量的复合最值问题，找出内层最值与算术平均数或几何平均数的不等关系，借助平均值不等式进行转化，是处理这类问题的常用方法．

3 设而不求法

对于双层最值问题，可以先设出内层最值，利用其最值性，建立关于内层最值的不等式，然后通过解不等式的方法求出外层最值．

注(1)把内层最值设出来，并不求出．如何利用已知条件寻找其满足的不等关系是正确解题的关键．

(2)对于例3，可以借助柯西不等式直接建立内层最值的不等式．

4 分类讨论法

首先确定多个不同基本变量(自变量)的大小关系，然后利用各变量相等找出分类讨论的分界点，再分类讨论确定最值．

例4已知实数a，b，c满足条件a+b+c=1，并且方程ax2+bx+c=0有实数根．记t=max{a，b，c}，求 t的最小值．

解(1)若 t=a，则

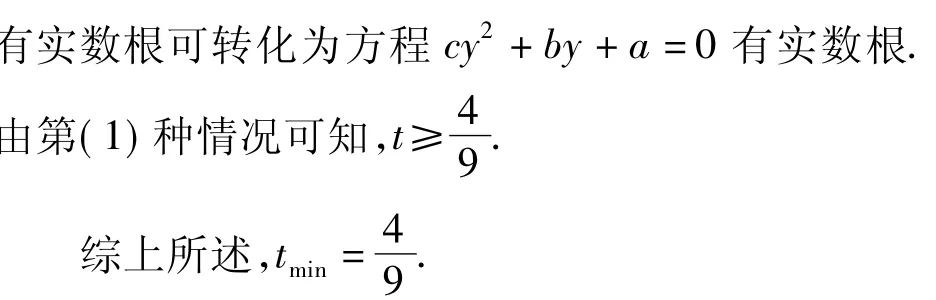
注通过讨论基本变量的大小关系，可确定出内层最值的表达式，再利用已知条件就能够求出外层最值．

5 赋值法

通过对函数的主变量赋予特殊函数值得到第二类参变量满足的不等式，再利用放缩法得到上界或下界，然后指出所得的界是能够取到的．

注对于内层函数含有绝对值符号的问题，常采用赋值放缩法进行求解．

6 猜想反证法

对一些复合最值问题，可根据问题的极端情况先猜出最值，然后给出证明．如果从正面不好证明，那么可以考虑用反证法解．

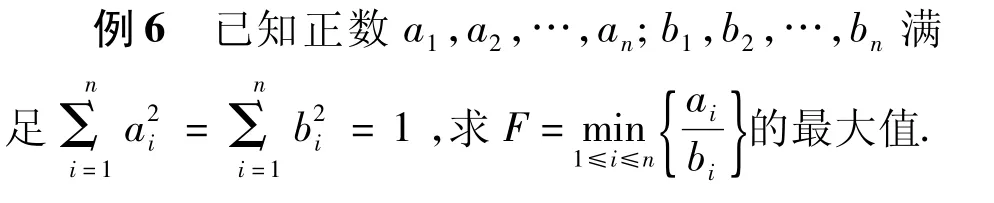
［1］ 叶军．数学奥林匹克教程［M］．长沙:湖南师范大学出版社，1998．