均值不等式几何解释的探究

●丁小刚 (奔牛高级中学 江苏常州 213131)

均值不等式几何解释的探究

●丁小刚 (奔牛高级中学 江苏常州 213131)

图1

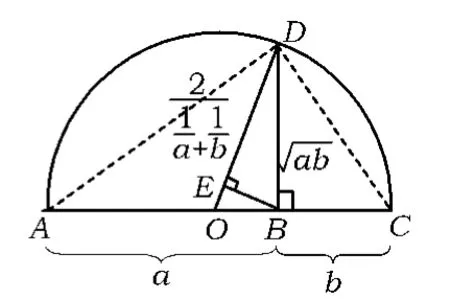
图2

教学至此，笔者觉得教科书给师生留下了较大的思维空间，教师不妨引导学生探究以下问题:

(1)均值不等式中的4种平均值的大小关系是否都能作出平面几何解释?

(2)均值不等式能用平面几何知识解释，那能否用解析几何知识解释?

经过师生的共同探究，得到了满意的结果．现将探究过程简述如下，仅供参考．

1 用平面几何知识解释均值不等式的探究过程

以上的探究过程让学生很受鼓舞．但是马上发

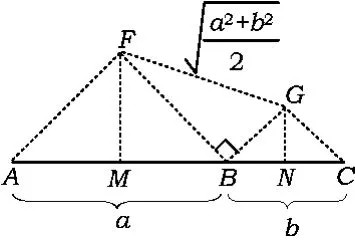
图3

在图 3中，分别以 AB，BC为斜边作等腰直角三角形△ABF和△BCG，连结FG．由M，N分别是AB和 BC的中点，得MNGF是直角梯形．因为

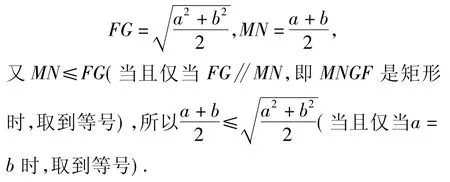
2 用解析几何知识解释均值不等式的探究过程

用平面几何知识解释均值不等式，教科书对此内容作了开拓性的提示，比较容易做到．现在要用解析几何知识解释均值不等式，无疑对师生都是一个挑战．经过一番努力，师生共同总结出下面3个注意点:

(1)为了便于应用解析几何知识，将均值不等式改写成:

若 x＞0，y＞0，则

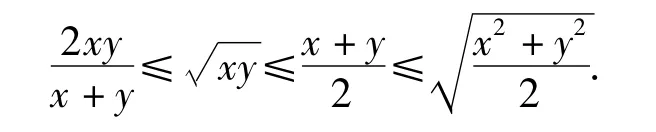
(2)解析几何的思想方法是建立点和坐标之间以及曲线和方程之间的对应关系，因此探究方向是考虑这4种平均值能否与相应的曲线方程联系起来，它们的大小能否用相应的点的坐标来表示．

如图4，考虑平面直角坐标系中的固定直线l:x+y=2m，以及双曲线族xy=c(c＞0)．

由图4可以看出，当双曲线与直线l只有一个公共点且 c取得最大值时的曲线，必定是在点Q(m，m)处与直线l相切的双曲线，此时c=m2，即当且仅当x=y=m时，不等式取到等号．

这一步探究的成功具有开拓性的价值，师生无不为之振奋．

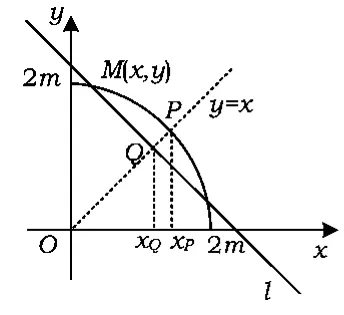
图5

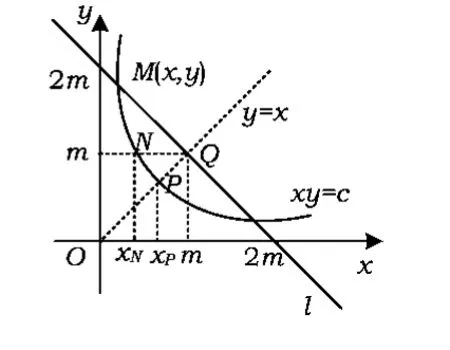
图6

如图5，考虑平面直角坐标系中的固定直线l:x+y=2m，以及圆系:x2+y2=2r2(r＞0)．令直线y=x与圆交于点 P(xP，yP)，交直线 l于点 Q(xQ，yQ)，同样直线l与圆必定有交点M(x，y)．因为

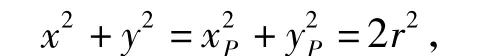
又 xP=yP，所以

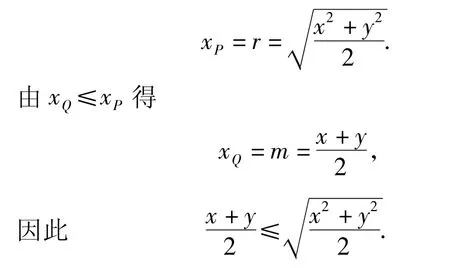
由图5可以看出，圆与直线l只有一个公共点，且r取得最小值的曲线必定是在点Q(m，m)处与直线l相切的圆，此时r=m．即当且仅当x=y=m时，不等式取到等号．

如图6，考虑平面直角坐标系中的固定直线l:x+y=2m，以及双曲线族 xy=c(c＞0)．令直线 y=x交双曲线于点P(xP，yP)，交直线l于点Q(m，m)．因为 xy=xPyP=c，又 xP=yP，所以

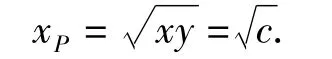
再设双曲线上纵坐标等于m的点为N(xN，m)．由m·xN=xy，得

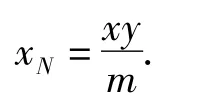
因为 xN≤xP，所以

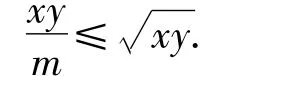
当且仅当双曲线与直线l相切，即x=y=m时，不等式取到等号．

以上是用点的坐标来比较4种平均值的大小，其实还可以利用曲线与直线的位置关系来比较这些平均值的大小．

探究活动结束后，笔者感触颇多．教科书中许多内容的陈述往往是美丽而冰冷的，火热的思考被淹没在形式化的海洋里．如何点燃和激起学生火热的思考，并欣赏数学中冰冷的美丽，是数学教学的一项基本任务．本文所探究的均值不等式的几何解释不过是沧海一粟．教科书中的珍宝可以说是俯拾即是，关键是要求教师做一个有心人，引领学生不断地去挖掘数学丰富的内涵，不懈地进行探索．

数学教学过程决定学生怎样看待数学学习以及对数学本质的认识．如果在教学中要求学生只是模仿和记忆，只是训练和操作，那么学生会把数学学习看成就是解题．这样的数学学习是枯燥的、与日常生活没有联系的．反之，如果注重教学过程，使学生理解知识的来龙去脉，寻求知识间的内在联系，建立完善的知识结构，那么学生就会逐渐地认识到数学知识是有着内部联系的整体，数学知识有着自身的发展规律，而这些又可以通过自己的努力去探究获得．这样的观念将会鼓励他们去消除数学知识的神秘感，激发他们勇于探索的勇气，引导他们寻找数学知识与现实世界的联系．这也正是一个优秀数学教师所要追求的理想的教学效果．

［1］ 柯朗(Courant，R．)，罗宾斯(Robbins，H．)．数学是什么［M］．汪浩，朱煜民，译．长沙:湖南教育出版社，1984．

［2］ 胡典顺，徐汉文．数学教学的过程特征和过程价值初探［J］．数学通讯，2007(23):1-3．