从一道高考题谈无字证明

●康小峰 (栟茶高级中学 江苏如东 226406)

从一道高考题谈无字证明

●康小峰 (栟茶高级中学 江苏如东 226406)

题目设a＞0，b＞0，则为 a，b的调和平均数，如图1，C为线段AB上的点，AC=a，CB=b，O为AB的中点，以AB为直径作半圆．过点C作AB的垂线交半圆于点D，连结OD，AD，BD．过点C作OD的垂线，垂足为E，则图中线段OD的长度为a，b的算术平均数，线段＿＿ 的长度是a，b的几何平均数，线段＿＿ 的长度是a，b的调和平均数．

(2010年湖北省数学高考理科试题)

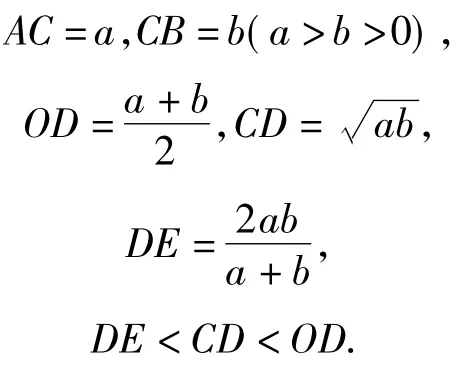
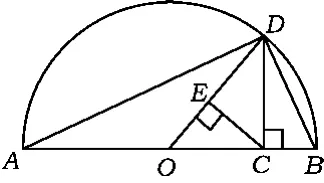
图1

这道题源于苏教版普通高中教科书《数学》必修5第3．4节．在讲解定理:“2个正数的算术平均数不小于它们的几何平均数”后，教材中给出了这一定理的一种几何解释．其实该题更为深刻的背景是近年来一些数学家特别关注的将数学命题用简单、有创意且易于理解的几何图形来呈现的无字证明(如图1)．无字证明问题源于20世纪90年代末美国《数学杂志》开辟的专栏:没有文字的证明(Proof without words)．无字证明古已有之，例如赵爽的“弦图”、毕达哥拉斯学派的“形数”等，均属典范．我们在学习中经常用到的“数形结合”方法和无字证明的关系也是比较密切的．从这道高考题的背景，我们能感受到无字证明为数学问题的解决提供了独特的视角:简洁、直观．

以往的高考试题中虽然有以数形结合思想来考查不等式几何意义的题目，但没有直接考查均值不等式几何意义的试题．在高三复习中，教师也可能很少注意到这一问题，因此大部分考生拿到此题无从下手，正确率就可想而知了．其实，苏教版数学教科书必修5第98页的探究拓展中就给出了一种典型的无字证明方案:

如图2，ABDC 为梯形，其中 AB=a，CD=b，设O为对角线的交点．若GH表示平行于两底且与它们等距离的线段(即梯形的中位线)，KL表示平行于两底且使梯形ABLK与梯形KLDC相似的线段，EF表示平行于两底且过点O的线段，MN表示平行于两底且将梯形ABDC分为面积相等的2个梯形的线段．试探究线段 GH，KL，EF，MN与代数式

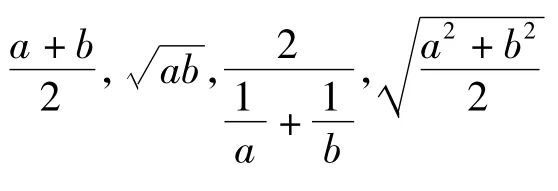
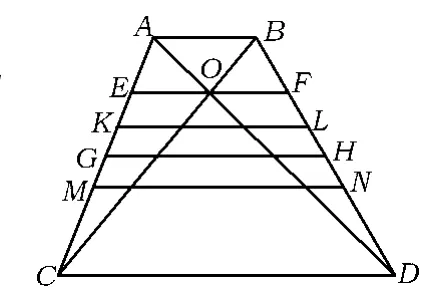
图2

之间的关系，并据此得到它们之间的一个大小关系．你能用基本不等式证明所得到的结论吗?

很多教师怕耽误教学进度对此问题视而不见，或在此一带而过，甚至认为是浪费时间而不愿和学生一起欣赏它，这就失去了一个极好地对学生进行无字证明教育的机会．因此，笔者认为可以在平时的课堂教学中适当引入一些无字证明．一来可以加深学生的印象，激发学生的学习兴趣;二来可以开拓学生的视野，发现数学的优美．这样学生在遇到此类问题时既能够从容面对，又不至于造成无谓的失分．美国家喻户晓的数学科普大师Martin Garder曾将无字证明这种图形视为“一瞥就懂”的图形，并认为很多时候一个繁复的证明在很多时候若能辅以一个几何图形，则后者的简洁与美妙几乎可以让读者一瞥即对定理的真实性了然于胸．这足以显现无字证明的巨大功效了．

既然无字证明有如此之大的功效，那么笔者接下来再举几例，供同行教学时参考．

例1“无字证明”三角公式(如图3，图4)．

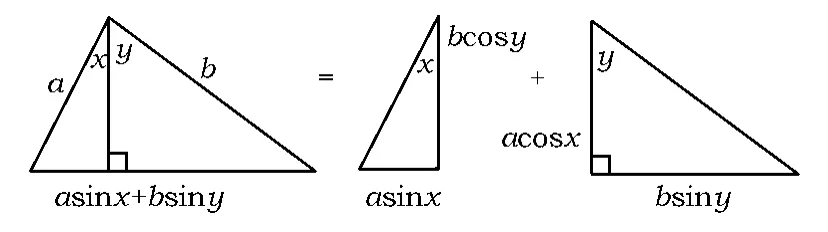
图3

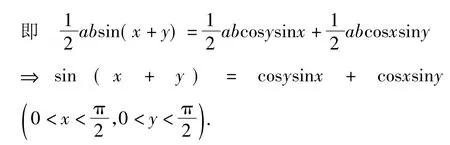
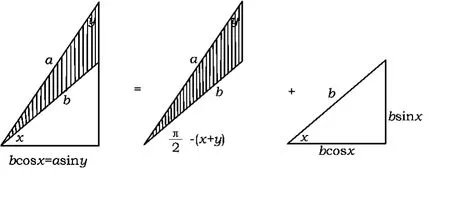
图4

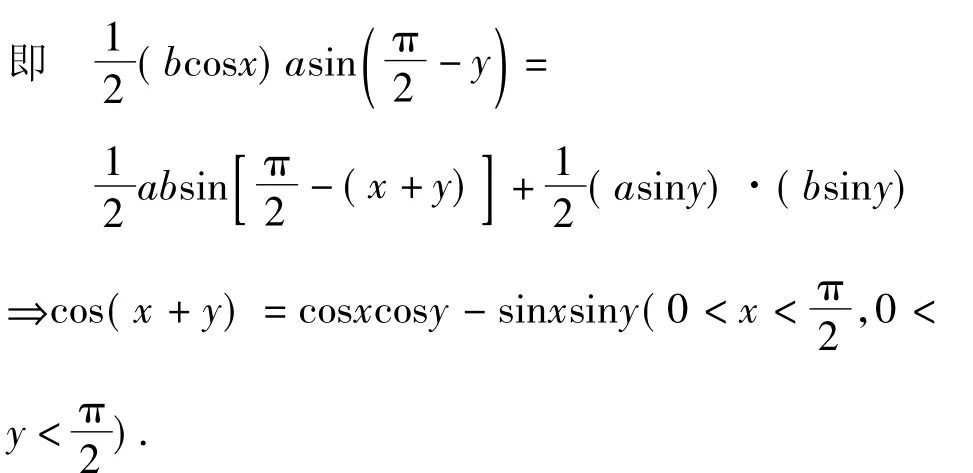
启示出入相补原理是中国数学特别是几何学最基本的原理之一，指的是“一个平面图形从一处移至他处，面积不变．又若把图形分割成若干块，则各部分面积的和等于原来图形的面积，因而图形移动前后诸面积间的和、差有简单的相等关系”．上述无字证明把三角形的面积公式、出入相补原理以及两角和的正弦、余弦公式紧密地联系起来，直观明了、易于理解．

例2“无字证明”余弦定理(如图5)．

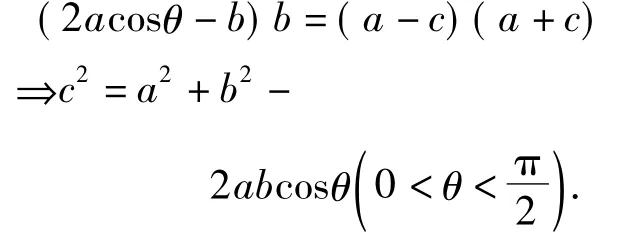
图5

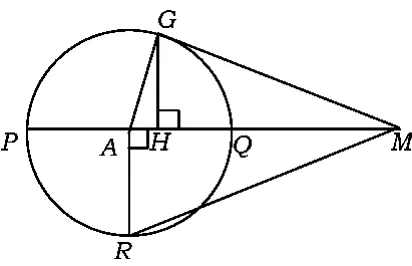
图6

启示余弦定理是三角形关于边角关系的命题，上述无字证明巧妙地将有关圆的相交弦定理和余弦定理联系起来．虽然图形所能表示的范围有限，但创意可谓无限．

例3图解均值不等式(如图6)．

启示均值不等式是最基本的不等式之一，是证明其他不等式和求解各类最值的重要依据．上述无字证明把圆、勾股定理以及均值不等式有机地结合起来，可谓“得意”而不“忘形”．

例4“无字证明”数列求和公式(如图7)．

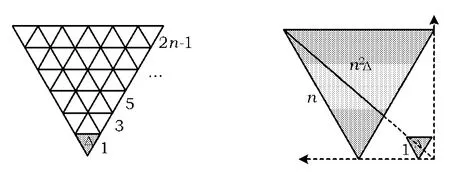
图7

启示图7利用三角形相似证明了等差数列的求和公式，为探究数列与图形之间的联系开辟了新道路．

例5图解三角求和(如图8)．

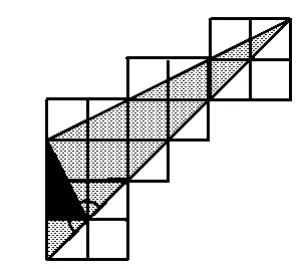
图8

启示借助于图形，3个角的关系跃然纸上，不得不令人惊叹图形的力量．

上面从4个角度给出了5道无字证明题，有兴趣的读者可以试着去构造一些优美的图形．尽管无字证明有一定的局限性(如例1中两角限制在锐角范围，例4中是特殊的等差数列)，但其数学价值不言而喻，借着可视化的感受及简单的数学概念常常能给学生留下深刻的印象，因而对我国当前中学数学教学具有重要的意义．

［1］ 吴文俊．九章算术与刘徽［M］．北京:北京师范大学出版社，1982．